基于改进单神经元自适应控制的光伏发电系统MPPT研究

王 玮， 沈 忱

(南京供电公司，江苏南京210003)

随着全球经济的发展，能源的需求与消耗越来越大，迫切需要寻找一种无污染、可替代的可再生能源。太阳能以取之不尽、用之不竭、清洁等优点成为全世界重点推广的新能源之一。而光伏发电技术是利用太阳能的最为公认的一种技术。但光伏电池的非线性及无规律的外界环境变化的特性，导致光伏电池不能稳定在最大功率点处，因此为了提高能量利用效率，需进行最大功率点跟踪（MPPT）控制。目前常用的MPPT法主要有固定电压法、扰动观察法、电导增量法等。固定电压法控制方法简单，但由于忽略了外界环境的变化，能量损失较大[1]。扰动观察法控制算法易于实现，但不能很好地适应外界环境的剧烈变化，且无法兼顾跟踪的快速性与精确性[1，2]。电导增量法能快速适应外界环境的变化，但无法选择合适的步长来兼顾跟踪的快速性与准确性[3，4]。除了以上几种方法外，目前也有一些文献将智能控制算法应用到MPPT中如：模糊控制法等。模糊控制法主要是模糊比例微分（PD）法，该方法能够快速地跟踪到最大功率点，但由于缺少积分控制会给系统带来稳态误差，跟踪精度不够，且模糊规则及隶属度函数的选择对跟踪效果影响较大[5]。文中提出了一种改进的单神经元自适应比例积分微分（PID）控制的方法来实现光伏电池的MPPT，该方法可以解决单神经PID控制存在跟踪速度较慢的问题，同时可以快速精确地适应外界条件的变化。

1 光伏电池模型建立

根据光伏电池的内部特性，采用光伏电池的单指数模型进行建模，图1为光伏电池的等效电路。由图1可得到光伏电池的I-U方程[6-8]：

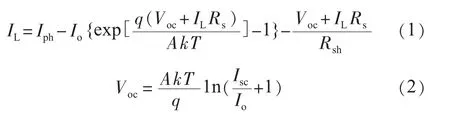
图1 光伏电池等效电路

式中：IL为光伏电池的输出电流；Iph为光生电流；I0为二极管的暗饱和电流；Isc为标况下电池的短路电流；Voc为光伏电池的开路电压；A为二极管特向因子；q为电子电荷量，1.6×10-19C；k 为波尔兹曼常数，0.86×10-4eV/K；T为绝对温度。

2 MPPT系统控制结构

为了减小控制算法的复杂度，针对两级式光伏发电系统的MPPT进行研究。其拓扑结构如图2所示，其中主电路部分是由光伏电池、电路以及负载或直流母线组成。控制部分主要是通过控制电路中的开关来调节占空比以调节光伏电池的输出电压Vout，实现光伏电池的MPPT。

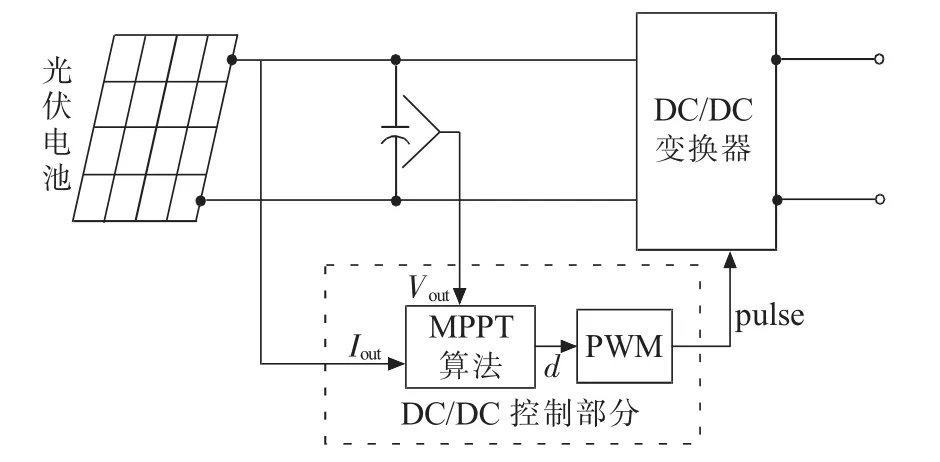
图2 MPPT控制结构

3 单神经元自适应PID控制方法改进

改进的单神经自适应PID控制主要思想是两段式方法即远离最大功率点处采用电导增量法，在最大功率点附近时采用单神经自适应PID控制法，该方法是利用电导增量法能够快速适应环境变化及单神经自适应PID控制可以提高跟踪稳态精度的优点，以实现各种环境条件下快速准确的MPPT。其控制结构如图3所示。

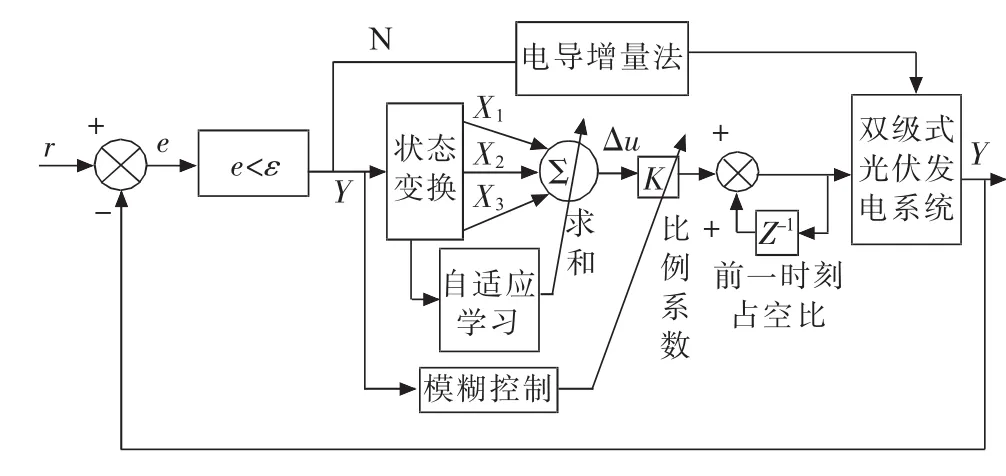
图3 改进单神经元自适应控制结构

3.1 单神经自适应PID控制算法实现

单神经自适应PID控制器是通过加权系数的调整实现自适应控制[9]。具体的控制算法如式（3—8），令给定 r=0；w1（k），w2（k），w3（k）分别为当前时刻对应的加权系数，ηI，ηP，ηD分别为 I、P、D 的学习率；K 为比例系数；d（k）为当前控制的占空比。其中式（3）为加权系数调整，式（4）加权系数平均值求取，式（5）为当前时刻的占空比，式（6—8）为当前状态量的变化。

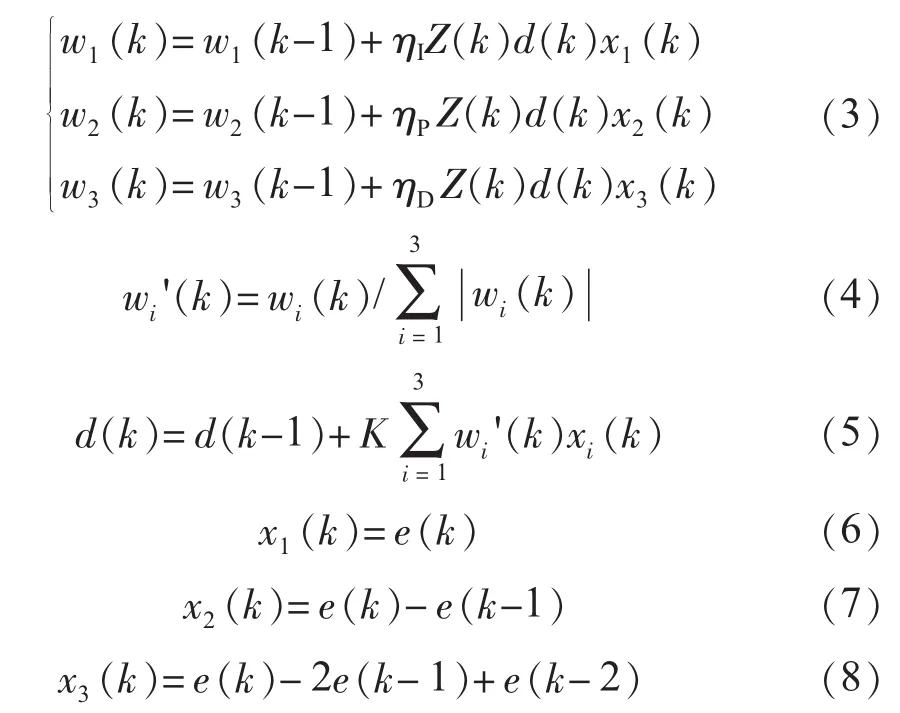
3.2 单神经元自适应PID控制方法的改进

单神经元自适应PID控制方法具有消除稳态误差的优点但又存在启动慢的缺点，文中在远离最大功率点处采用电导增量法来提高系统跟踪速度且能快速适应环境的变化。此外单神经元自适应控制方法比例系数K的选择对系统跟踪性能影响较大，K值过小会影响跟踪速度，K值过大会影响稳态误差[9，10]，文中依据误差的大小，结合模糊规则选择合适的K值来满足系统要求。具体算法流程图如图4所示。图5为输入量e的隶属度函数，图6为输出量K的隶属度函数，表1为模糊规则，其中采用5个模糊语言变量分别为正大（PB）、正小（PS）、零（Z）、负小（NS）、负大（NB）。

4 仿真分析

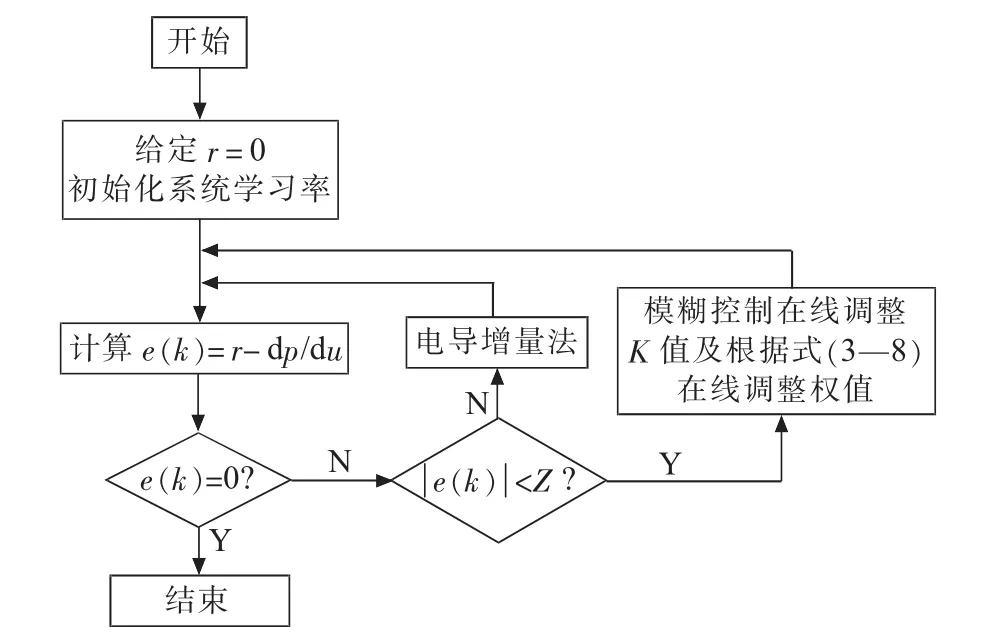
图4 改进单神经元自适应PID算法流程

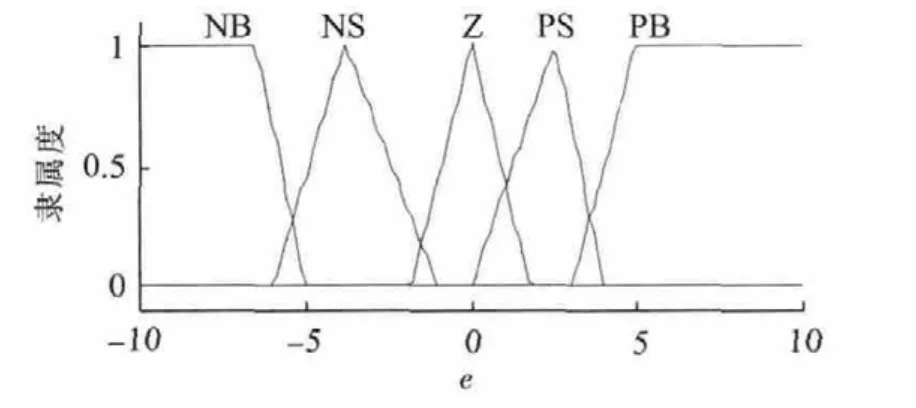
图5 输入量e隶属度函数

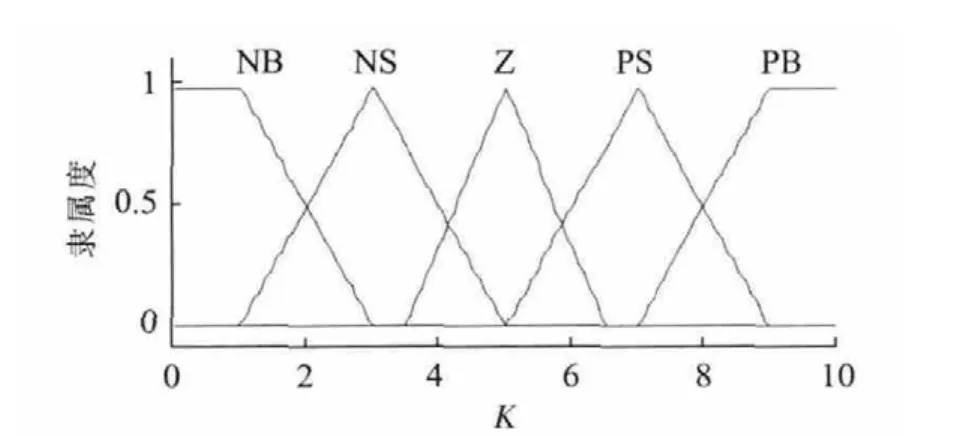
图6 输出量K隶属度函数

表1 模糊规则

利用MATLAB仿真工具箱建立了100W光伏电池仿真模型，在外界环境变换的条件下，分别对扰动观察法、单神经元自适应算法及改进单神经自适应方法进行了仿真。用斜坡函数表示光照变化，假设温度稳定在25℃，0.25 s时光照强度从1000W/m2下降到600 W/m2，3种方法的仿真对比结果图如7所示。

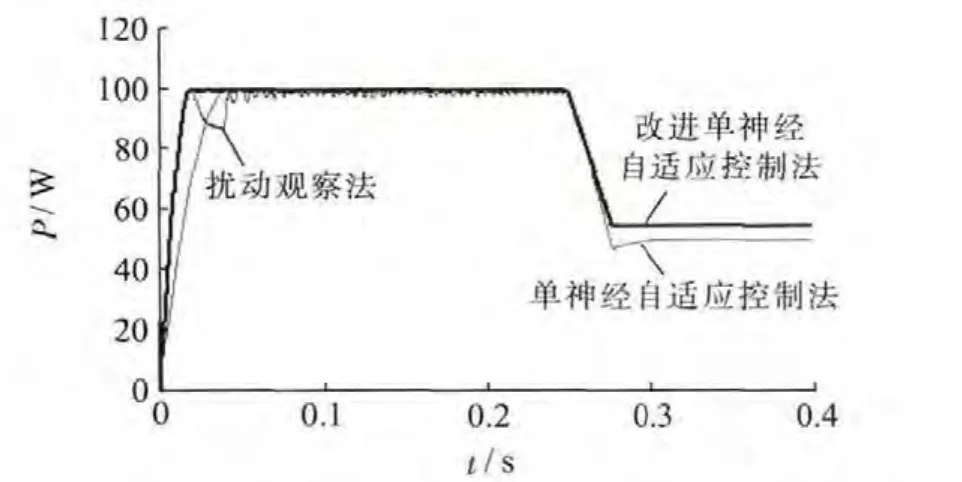
图7 不同MPPT仿真结果比较

由图7可见，扰动观察法在0.08 s时才能跟踪到最大功率点，且在最大功率点处存在较大的功率波动。单神经自适应控制算法在0.05 s时能跟踪到最大功率点，且在最大功率点处功率波动较小，实现了PID控制稳态误差较小的优点。但单神经元自适应控制法由于K取值的问题，在外界环境变化下存在功率跟踪误差。改进的单神经元自适应方法在0.02 s时实现了快速精确的MPPT，且能够快速精确地响应外界条件的变化，不存在功率跟踪误差。因此将改进的单神经自适应控制算法应用于光伏发电系统MPPT中，能解决传统方法扰动步长带来的不能兼顾快速性与精确性的问题，同时可以改善单神经元自适应控制启动慢及外界条件变化下功率跟踪准确性问题。

5 结束语

针对传统MPPT方法存在的缺陷，提出了一种改进的单神经元自适应控制算法。利用电导增量法能够快速响应外界条件变化，单神经元自适应法可以消除稳态误差的优点实现光伏发电系统的MPPT。利用MATLAB仿真工具对改进单神经自适应控制方法进行了仿真比较，结果表明该方法不仅能够快速响应外界条件的变化，快速跟踪到最大功率点，并在最大功率点处的功率波动小，稳态误差小。

[1]张 兴，曹仁贤.太阳能光伏并网发电及逆变控制[M].北京：机械工业出版社，2011：30-35.

[2]SIC T.Simulation Research on OutputCharacteristicsof Photovoltaic Array and MPPT Control[J].EastChina Electric Power，2010(2)：0284-0288.

[3]崔 岩，蔡炳煌，李大勇，等.太阳能光伏系统MPPT控制算法的对比研究[J].太阳能学报，2006，27(6)：535-539.

[4]陈爱龙.光伏发电系统MPPT的技术的研究与实现[D].成都：电子科技大学，2011.

[5]袁晓玲，陈 宇，宋鹏飞，等.带修正函数的模糊控制在光伏发电 MPPT 中的应用[J].可再生能源，2012，30(9)：16-20.

[6]王长江.基于MATLAB的光伏电池通用数学模型[J].电力科学与工程，2009，25(4)：11-14.

[7]赵争鸣，刘建政.太阳能光伏发电及其应用[M].北京：科学技术出版社，2005：109-117.

[8]苏建徽，余世杰，赵 为，等.硅太阳电池工程用数学模型[J].太阳能学报，2001，22(4)：409-412.

[9]王永骥，凃 健.神经元网络控制[M].北京：机械工业出版社，1998：55-60.

[10]王婵娟，王 强，傅承毓.单神经元模糊PID控制在光电跟踪系统中的应用[J].光电工程，2006，32（2）：33-36.