综合灾情指数——一种自然灾害损失的定量化评价方法*

张 鹏，张云霞，孙 舟，陆 野

（民政部国家减灾中心，北京100124）

综合灾情指数
——一种自然灾害损失的定量化评价方法*

张 鹏，张云霞，孙 舟，陆 野

（民政部国家减灾中心，北京100124）

自然灾害损失评价涉及人口、农业、房屋、经济等多项灾情指标，是典型的多元指标综合分析问题。如何设计合理的定量化评价指数，对灾害风险管理、损失评估和相关政策制定，具有重要意义。现有灾情评价方法和灾情指数，或对量纲差异较大的灾情指标敏感，或无法同时对不同区域的灾情时空分布进行比较，缺少综合性、兼顾时空分布的评价方法。针对上述问题，提出了一种新的基于几何平均的综合灾情指数计算方法。相较现有方法，该文提出的指数可同时在时间和空间两个维度对给定区域的灾害损失进行定量化的评价，且对指标分布偏倚的多元灾损数据不敏感。在2014年我国分省洪涝（含地质灾害）损失数据上的计算结果验证了新指数的有效性。

自然灾害；损失评价；综合灾情指数；几何平均

1 研究背景

自然灾害造成的承灾体的损失往往涉及人员、农业、房屋、经济等多个方面，因此，灾情作为承灾体损失的统计，是多指标构成的多元统计数据。灾后救助决策制定常需要对灾害损失程度进行量化评估，以判断受灾程度的轻重。而仅依赖于单一指标很难对受灾程度形成全面的描述，这就需要从多元灾情数据中形成单一指标，才能提供可量化的评估依据。因此，如何合理设计一种能全面、客观反映承灾体各方面损失的指数，是灾害损失评价面临的关键问题。

目前，研究界已提出了多种方法，用于从多元灾损统计数据中建立单一量化指标，主要可划分为两类。第一类是建立灾害损失的等级划分方法，马宗晋等［1］提出了灾度概念并给出了灾度等级的判别方法，依据死亡人口和直接经济损失将自然灾害的灾情分为5个灾度；赵阿兴等［2］在灾度基础上提出灾损率概念，并建立灾损率的等级划分标准，用以标度自然灾害相对损失；于庆东［3］对灾度模型进行了改进和扩展，将线性判别域改为圆判别域，扩展了灾度模型的计算维度；冯利华［4］提出了灾级指标，通过对死亡、伤害和直接经济损失指标的对数值进行折算后，再计算折算值的均值得出；任鲁川［5］将模糊数学中的模糊度模型引入到灾害损失等级划分中，将各单项指标分级后，通过建立模糊度矩阵，实现对灾情的综合评价分级；张弛等［6］将可变模糊集模型应用到灾害损失的分级评价当中，徐冬梅等［7］进一步将该模型应用于洪水灾害的损失评价；邱玉珺等［8］提出了量化灾情强度指数模型，通过建立灾次指数矩阵和灾种指数矩阵，给出了多区域多灾种发生强度的评价方法；魏庆朝等［9］提出一种灾害综合定量指标，通过计算死亡人数、伤害人数、灾害损失持续时间和综合经济损失四个因子的归一化均值得出；杨仕升［10］将灰色关联度模型应用于灾害损失分级评价；李柞泳等［11］使用物元分析法进行灾情评估，将灾害损失划分为三种类型。

图1 综合灾情指数计算图示

第二类是建立连续的指数模型，王静爱等［12］基于1949-1990我国县域灾害发生次数，建立了自然灾害成灾指数，包括归一化多度、灾次比和均灾次的平均值，并对长时间序列下灾害发生的频率进行了评价；袁艺［13］基于2000-2007全国分省灾情数据，使用加权平均模型，建立了灾情绝对指数和相对指数，对灾害的空间分布进行了探究；程立海等［14］提出了一种综合指数的计算方法，通过计算各灾情指标归一化后的加权平均值，对汶川地震的分县受灾强度进行了评估；张星［15］在灾情指标的加权平均模型中引入熵权，提出了一种灾情综合评价模型；王莺等［16］通过假设月降水量服从Person分布，对降水量进行正态化处理，计算了1960-2010年石羊河流域降水量的Z指数，对该地区的旱涝等级进行了划分；廖永丰等［17］基于2000-2011年自然灾害情况统计数据，建立了绝对灾情指数和相对灾情指数两个定量化度量指标，对全国各省受灾情况进行了分级；汤家法等［18］对2013年7月北川县1318个居民点的6项地质灾害风险指标进行主成分分析，使用主成分得分对分乡镇的灾情进行排序。

尽管上述工作在灾害损失评价的特定问题中取得了较好的效果，但仍面临以下问题。①等级划分模型计算得出的指数是离散型的，不能提供连续的度量，因此在多区域比较时无法提供精细化的依据；②加权平均模型对于个别指标分布偏大的灾情数据敏感，易造成仅有一项或几项指标明显偏高的区域指数偏大，综合性和客观性受到影响；③受归一化因子局限，现有指数仅能对某段时间内或某个地区内的对象进行比较，尚没有指数能同时在时间和空间两个维度具备评价能力。

针对上述问题，本文基于民政系统2000年以来年度会商核定数据，提出了一种新的层级式综合灾情指数计算方法。通过历史和经济本底数据对灾情指标校准和归一化后，使用几何平均模型，分别计算人口、农业、房屋和经济4个次级指数，再对其进行二次平均得到综合灾情指数。相较现有方法，本文提出的灾害损失评价指数具有以下三个优势：①可同时在时空两个维度对评价对象的损失程度进行比较；②对灾情指标分布偏倚的数据不敏感，评价能力更加综合；③指数连续分布，自身度量具备实际意义并可用于评价对象的排序。对2014年我国洪涝（含地质灾害）分省灾情指数的计算和分析结果证明了本文提出方法的有效性和合理性。

2 综合灾情指数计算方法

2.1 方法概述

综合灾情指数（Natural Disaster Index，NDI）是对给定时间范围内一个区域受灾情况的总体衡量尺度。给定灾种，NDI从四个维度衡量一个区域的平均受灾损失程度，包括人口、农业、房屋和经济。我们以省级区域为评价对象，以2000-2014年国家减灾委会商核定的年度全国分省灾情数据为基础，计算分省综合灾情指数。其计算步骤如图1所示。

综合灾情指数的计算包括2层。对给定评价区域，首先选取受灾人次、死亡失踪人口、紧急转移安置人次、农作物受灾面积、农作物绝收面积、倒塌房屋间数、损坏房屋间数、直接经济损失作为基本指标，按照人口、农业、房屋、经济4个维度分别计算出相应的维度指数；然后由维度指数综合计算出最终的灾情指数。

2.2 计算步骤

2.2.1 数据预处理

数据预处理阶段包括2个步骤：①对零值指标的处理；②对直接经济损失指标的折算。首先，本文基于几何平均模型计算综合灾情指数，要求用于计算的多元数据各项指标非零，因此需将所有灾情数据中的0值替换为一个小值。具体替换规则见表1。其次，为消除通货膨胀造成的经济损失货币值变化，使用国家统计局公布的累积CPI指数对直接经济损失进行折算。记第i年第j省的直接经济损失为E0，则折算公式为

式中：E为折算后的直接经济损失，CPIi为当年的累积CPI指数（以1999年为基准）。

2.2.2 指标归一化

由于灾情数据为多元统计量，为保证各指标均在统一的量纲下进行计算，需将各指标进行归一化处理。

式中：x*为归一化指标，x为指标原始值，xmax和xmin分别为该指标在2000－2014年间的最大值和最小值。本文中计算的洪涝综合灾情指数使用的数据最大和最小值见表1。

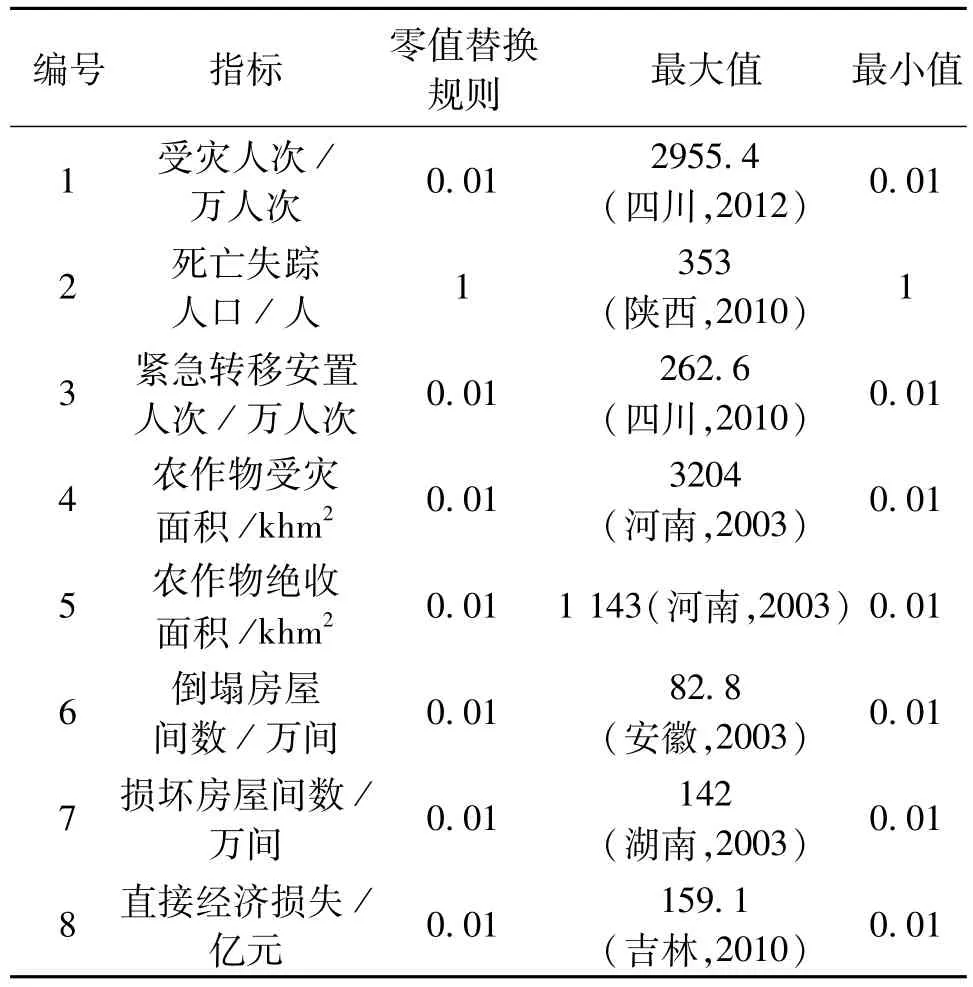
表1 零值替换规则和指标最大／最小值

2.2.3 计算各维度指数

本文使用几何平均模型计算各维度指数，即维度指数为该维度下各归一化指标值的几何加权平均值。

相比算数平均值，几何平均值对单一指标明显偏大的数据不敏感，不易出现均值向具有偏倚分布数据大幅倾斜的情况。这一策略已应用于近年来联合国人类发展署公布的人类发展指数计算中［19－22］，取得了很好的效果。

各维度指数计算公式如下：

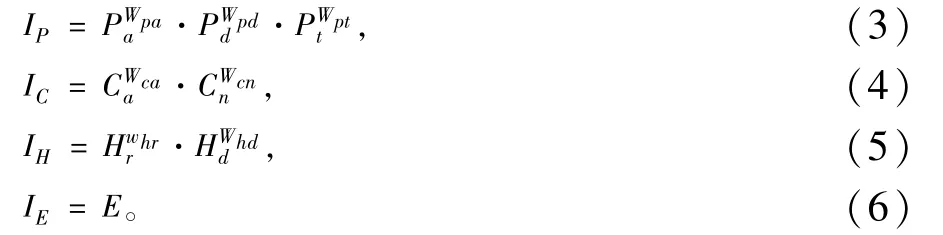
各项符号的含义和权重取值参见表2。

2.2.4 计算综合灾情指数

由2.2.3节计算得出四个维度指数后，按照2.2.2节中的方法，使用式（2）分别对各维度指数进行归一化。由于评价对象的维度指数不存在零值，因此不需要进行零值替换处理。最终的综合灾情指数为4个维度指数归一化后的几何平均值，计算公式为

3 2014年洪涝（含地质灾害）灾情指数分析

我们以国家减灾委会商核定的2000－2014年洪涝（含地质灾害）全国分省灾情数据为基础，计算2014年我国分省洪涝灾害综合灾情指数，计算结果如图2所示。

同时，我们对2000－2014全国洪涝灾害总体灾情指数序列，计算其均值和方差，建立了该时间序列的统计模型，具体见图3。

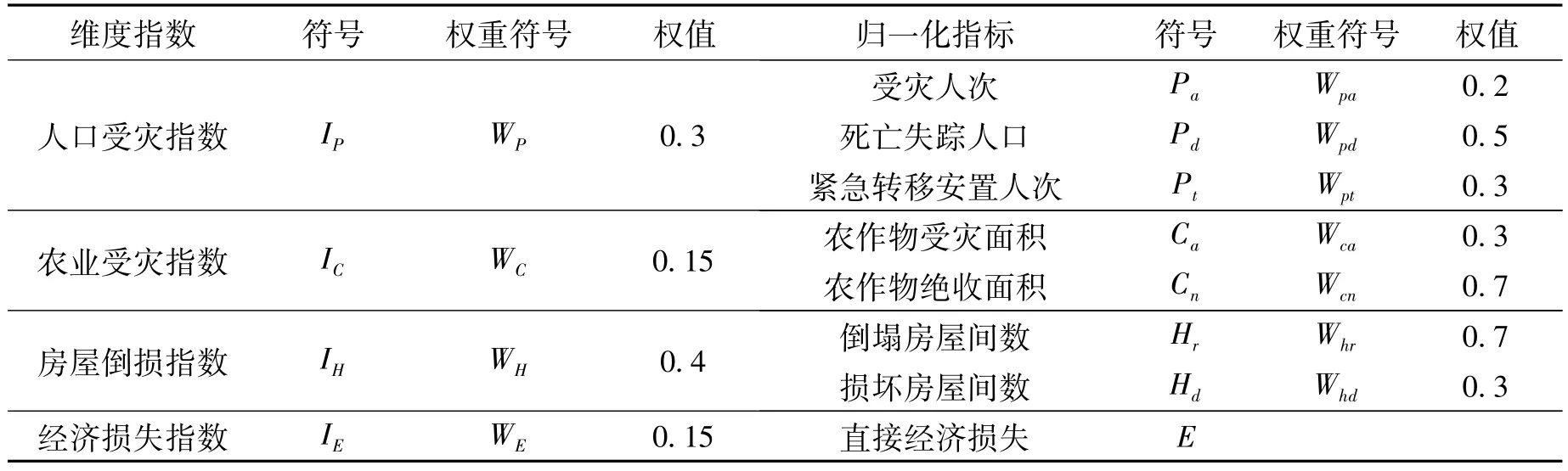
表2 式（3）～式（7）中符号含义及权重取值

图2 2014年分省洪涝灾害综合灾情指数分布示意图（未统计港澳台地区）

图3 2000-2014全国洪涝灾害综合灾情指数折线图

由上述计算结果和图示，我们可分析得出以下结论。

（1）2014年我国洪涝（含地质灾害）灾情较2013年明显偏轻，且较常年偏轻，综合灾情指数为2000年以来历史最低值。这从灾情指标的历史分布也可得到验证，今年我国洪涝（含地质灾害）造成的农作物受灾面积、绝收面积和倒塌房屋间数均为2000年以来历史最低值，受灾人次、死亡失踪人口、损坏房屋间数为历史次低值，紧急转移安置人次为历史第三低值。

（2）受极端强降雨天气影响，局部地区灾情较重，特别是主汛期南方多次大范围降雨过程和华西秋雨过程，造成灾害损失主要集中在江西、湖南、广东、广西、重庆、四川、贵州、云南、陕西9省（自治区、直辖市）。从综合灾情指数分布看，除黑龙江外，大于0.17的区域均为上述省区市。

（3）汛期局地强降雨在南方频发引发地质灾害，造成大量人员死亡失踪，湖南、重庆、四川、云南、贵州尤为严重，5省市人口维度指数明显偏高；黑龙江和湖南作为北方和南方粮食生产大省，农业损失较大，农业维度指数明显偏高；南方大范围降雨和华西秋雨过程造成灾区房屋倒损情况突出，房屋维度指数与综合灾情指数分布基本保持一致；湖南、广东、贵州多地城市遭受内涝，经济密集区受灾较重，造成经济维度指数偏高。

上述结论也与国家减灾委办公室公布的2014年我国自然灾害形势分析相符，说明了本文提出的综合灾情指数的有效性和准确性。

4 结论

本文中，我们针对自然灾害损失的定量化评价问题，提出了一种基于几何平均模型的综合灾情指数计算方法，实现了对给定区域多元灾情数据的单一量化指标计算。相较现有方法，本文提出的指数可同时在时间和空间两个维度对评价对象的灾损进行比较和分析，同时对灾情指标分布偏差较大的数据不敏感。对2014年全国分省洪涝灾害综合灾情指数的计算和分析结果，验证了本文提出方法的有效性。在下一步工作中，我们考虑将本文提出的指数计算方法推广至单个案例和分县的灾害损失评价，并对指数的平滑性进行改进。

参考文献：

［1］ 马宗晋，李闵锋.自然灾害评估、灾度和对策，中国减轻自然灾害研究［C］／／全国减轻自然灾害研究讨论会论文集.北京：中国科学技术出版社，1990.

［2］ 赵阿兴，马宗晋.自然灾害损失评估指标体系的研究［J］.自然灾害学报，1993，2（3）：1-7.

［3］ 于庆东.灾度等级判别方法的局限性及其改进［J］.自然灾害学报，1993，2（2）：8-11.

［4］ 冯利华.灾害损失的定量计算［J］.灾害学，1993，8（2）：17-19.

［5］ 任鲁川.灾害损失定量评估的模糊综合评判方法［J］.灾害学，1996，11（4）：5-10.

［6］ 张弛，宋绪美，李伟.可变模糊评价法在洪涝灾情评价中的应用［J］.自然灾害学报，2008，17（5）：34-39.

［7］ 徐冬梅，陈守煜，邱林.洪水灾害损失的可变模糊评价方法［J］.自然灾害学报，2010，19（4）：158-162.

［8］ 邱玉珺，王静爱，邹学勇.区域灾情评价模型［J］.自然灾害学报，2003，12（3）：48-53.

［9］ 魏庆朝，张庆珩.灾害损失及灾害等级的确定［J］.灾害学，1996，11（1）：1-5.

［10］杨仕升.自然灾害不同灾情的比较方法探讨［J］.灾害学，1996，11（4）：35-38.

［11］李祚泳，邓新民.自然灾害的物元分析灾情评估模型初探［J］.自然灾害学报，1994，3（2）：28-33.

［12］王静爱，史培军，王平，等.1949-1990年中国自然灾害时空分异研究［J］.自然灾害学报，1996，5（1）：1-7.

［13］袁艺.2000-2007年省级区域自然灾害灾情分析［J］.自然灾害学报，2011，20（1）：156-162.

［14］程立海，唐宏，周廷刚，等.自然灾害强度的评估方法及应用——基于综合灾情指数的研究［J］.自然灾害学报，2011，20（1）：46-50.

［15］张星.自然灾害灾情的熵权综合评价模型［J］.自然灾害学报，2009，18（6）：189-192.

［16］王莺，赵福年，姚玉璧，李耀辉.基于Z指数的石羊河流域干旱特征分析［J］.灾害学，2013，28（2）：100-106.

［17］廖永丰，赵飞，王志强，李博，吕雪锋.2000-2011年中国自然灾害灾情空间分布格局分析［J］.灾害学，2013，28（4）：55-60.

［18］汤家法，王沁.2013年北川聚落空间的地质灾害灾情分析.灾害学，2015，30（1）：87-91.

［19］United Nations Development Programme.Human Development Report2014［EB／OL］.［2014-12-22］.http：／／hdr.undp.org／en／2014-report.

［20］United Nations Development Programme.Human Development Report2013［EB／OL］.［2014-12-22］.http：／／hdr.undp.org／en／2014-report.

［21］United Nations Development Programme.Human Development Report2011［EB／OL］.［2014-12-22］.http：／／hdr.undp.org／en／2014-report.

［22］Klugman J，Rodríquez F，ChoiH.The HDI2010：new controversies，old critiques［J］.Journal of Economics Inequality，2011，9（2）：249-288.

Natural Disaster Index：A Quantitative M easure for Assessing Natural Disaster Losses

Zhang Peng，Zhang Yunxia，Sun Zhou and Lu Ye
（National Disaster Reduction Center of China，Ministry of Civil Affairs，Beijing 100124，China）

Assessments of natural disaster losses are related to various aspects，such as population，crops，houses，and economics，which are typicalmulti-variant analysis issues.How to design an overall and reasonable assessing index is of crucial importance to disaster risk management，loss assessment and policy making.Current approaches are either sensitive to data of biased measurements or not applicable to simultaneously temporal-special comparisons.In this paper，we propose a new computationalmodel of natural disaster index（NDI）based on geometric means.Compared with state-of-the-art，the proposed one can assess the losses of a region quantitatively along time and space at the same time，and it is robust tomulti-variant datawhich has biased distributions ofmeasurements.Simulations conduced on the real loss data of the 2013 floods in China validate the effectiveness of the proposed NDImethod.

natural disaster；assessment of disaster loss；comprehensive disaster index；geometric mean

X43

A

1000-811X（2015）04-0074-05

10.3969／j.issn.1000-811X.2015.04.015

张鹏，张云霞，孙舟，等.综合灾情指数——一种自然灾害损失的定量化评价方法［J］.灾害学，2015，30（4）：74-78.［Zhang Peng，Zhang Yunxia，Sun Zhou，et al.Natural Disaster Index：A Quantitative Measure for Assessing Natural Disaster Losses［J］.Journal of Catastrophology，2015，30（4）：74-78.］

2015-03-17

2015-04-24

国家自然科学基金“基于拓扑空间表示的我国洪涝灾害时空分布规律挖掘与可视化研究”（41201552）；国家自然科学基金“基于GRACE水循环时变特征的长江流域水旱灾害风险研究”（41174013）

张鹏（1984-），男，山东济南人，助理研究员，理学博士，主要从事灾害风险管理和灾情数据分析.

E-mail：zhangpeng＠ndrcc.gov.cn