平均入射角道集PP波与PS波联合反演

石瑛， 芦俊*， 杨震， 杨春

1 中国地质大学（北京）能源学院，海相储层演化与油气富集机理教育部重点实验室， 北京 1000832 中国地质大学（北京）地球物理与信息技术学院， 北京 100083



平均入射角道集PP波与PS波联合反演

石瑛1， 芦俊1*， 杨震1， 杨春2

1 中国地质大学（北京）能源学院，海相储层演化与油气富集机理教育部重点实验室， 北京 1000832 中国地质大学（北京）地球物理与信息技术学院， 北京 100083

在界面两侧地层的弹性参数弱反差的假设难以成立的情况下，本文提出用平均入射角道集进行PP波与PS波的联合反演．首先，在PP波与PS波AVA（amplitude versus angle，振幅随入射角变化）道集的基础上，分别选择小入射角范围与大入射角范围的AVA道集进行局部加权叠加，以获得由两个角度组成的平均入射角道集，并作为后续反演的输入数据．然后，再通过最小二乘原理建立了PP波与PS波联合反演目标函数，推导了模型修改量的向量公式，建立了平均入射角道集联合反演的流程．模型数据与实际数据的测试结果表明：在信噪比较低、地层弹性参数反差较大、层厚较薄的情况下，该反演方法的精度在很大程度上超过了基于近似反射系数的反演方法，为复杂油气藏勘探提供了新的思路．

平均入射角； 联合反演； PS波； 反射系数； 最小二乘

1 引言

随着我国油气田勘探开发的不断深入，构造油气藏越来越少，致密油、页岩气、煤层气等非常规油气资源已经成为勘探的重要方向（赵波等，2012）．这些油气储层一般都为薄互层储层，对薄互层反射，常常出现“伴随相位”（钱荣钧，1993）和“红波谷”（李弘等，2014）的现象，这造成了地震反演与解释上的误差．所以地震勘探的技术手段需要不断的发展，以应对日益复杂的油气勘探问题．在诸多地震勘探新技术中，多分量地震技术在解决复杂储层的勘探问题上表现出明显的优势（张永刚等，2004；李景叶等，2005）．大量的理论研究表明：利用多分量地震得到的PP波与PS波进行联合AVO（amplitude versus offset，振幅随偏移距变化）反演可以提供可靠的纵、横波速度以及密度信息，并派生出更多的反映地层岩性与含流体性的属性参数，这在很大程度上降低了地震解释的多解性，为复杂油气藏的预测提供了新的思路（Du and Yan，2013；张广智等，2014）．

多波AVO反演的基础是通过Zoeppritz方程求解地震反射系数，但该方程的形式比较复杂，没有给出反射系数与地层弹性参数之间的“显式”关系．所以国内外研究AVO反演的一个重要方面是对Zoeppritz方程进行近似，以获得反射系数与地层弹性参数之间的线性关系（Wang，1999）．这其中，最常用的近似公式是Aki-Richards近似公式（Aki and Richards，1980）．该公式是在地层界面两侧的弹性参数为弱反差的假设基础上建立的，可用来从反射系数直接反推单界面两侧纵、横波速度以及密度变化量．该理论在纵波上首先得到突破，并在实际勘探中得到充分应用．Shuey（1985）建立了用纵波AVO曲线的斜率和截距检测油气的理论．Smith和Gidlow（1987）提出通过PP波数据的加权叠加来计算纵、横波波阻抗以及其他的弹性参数．但上述方法由于采用了单一的纵波波场，地震解释的多解性问题较多，国内外学者一直考虑联合利用纵波与转换横波的联合AVO反演来降低解释的多解性．Stewart（1990）在纵波速度与密度的Gardner关系基础上，将Aki-Richards反射系数公式里的密度项用纵波速度的线性关系式替换，建立了加权叠加联合反演公式，得到了更为直接的多波叠前反演纵、横波速度的方法．Fatti等（1994）基于Gardner公式，在多波反射系数公式中消除了密度项，得到纵、横波波阻抗两参数叠前联合反演方法．郑晓东（1991）通过级数展开用入射角对P-SV波反射系数进行了近似，消除了横波角度，促进了线性AVO反演的发展．芦俊等（2010，2011）基于PP波与PS波反射系数近似公式反演了煤系地层的岩性与物性参数．徐善辉等（2012）利用TTI（tilt transverse isotropy，具有倾斜对称轴的横向各向同性）介质的反射系数近似公式进行了PS波的AVO分析．Zhi等（2013）用精确的Zoeppritz方程反演了地层界面上弹性参数的反差．侯栋甲等（2014）研究了基于贝叶斯理论的叠前多波联合反演弹性模量方法．大量的国内外文献表明：基于反射系数的近似公式的多波联合AVO反演已经得到充分的发展（Veire and Landrø，2006；刘洋等，2012；印兴耀等，2014），一些商业软件，如Jason、HRS等，已经推出可工业化应用的反演模块，服务于油气田的勘探开发．

虽然PP波与PS波联合AVO反演在理论上具有明显的先进性，但是在实际应用时见效并不明显．原因主要存在于以下两个方面：（1）首先是PS波入射角道集的信噪比较差，降低了联合反演的可靠性．AVO反演需要获得高质量叠前道集作为保障，但现在处理水平尚难以保证PS波的AVA道集具有较宽的入射角范围，并且信噪比较高．（2）另一个原因是反演中用到的反射系数近似公式都是建立在弱反差的假设前提下，无法适用于强反差的地层界面．很多储集层，如含煤地层、非固结砂岩地层、火成岩与页岩地层等，其弹性参数与围岩的差异较大，导致基于Aki-Richards反射系数近似公式的AVO反演方法出现较大的误差．针对上述问题，本文开展基于平均入射角道集的PP波与PS波联合反演方法的研究，用两个角度组成的平均入射角道集，基于精确的PP波与PS波反射系数，联合反演地层的纵波速度、横波速度与密度参数．

2 方法原理

本文提出的联合反演方法的输入数据是平均入射角道集，然后用一个统一的目标函数，将PP波与PS波的正演道集与实际数据平均入射角道集之间的残差结合在一起，基于Zoeppritz方程计算的精确PP波与PS波反射系数，进行纵波速度、横波速度以及密度的同时最小二乘反演．在反演过程中，通过多次迭代修改初始模型，使得目标函数达到最小．

2.1 PP波与PS波的平均入射角道集

在各向同性介质中，当一个平面纵波倾斜入射到两种介质分界面时，会产生四种波，即反射纵波、反射横波、透射纵波和透射横波（如图1所示），且满足Snell定律（Aki and Richards，1980）：

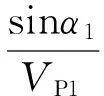
（1）

其中，p为射线参数，VP1和VS1分别为上层介质纵、横波速度，VP2和VS2分别为下层介质的纵、横波速度，ρ1和ρ2分别为上、下层介质的密度，α1和α2分别为纵波入射角（反射角）和透射角，β1和β2分别为横波反射角和透射角．

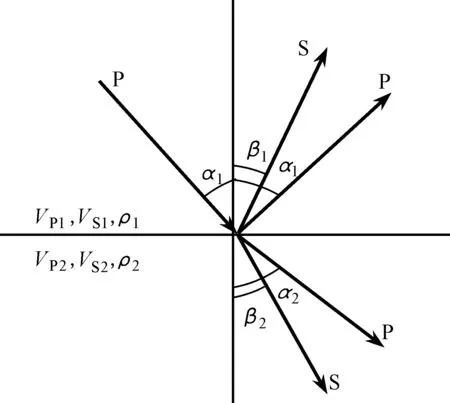
图1 P波在介质分界面上的反射与透射

令纵波反射系数为RPP、转换横波反射系数为RPS、纵波透射系数为TPP和转换横波透射系数为TPS，则Zoeppritz矩阵方程（Aki and Richards，1980）为

（2）

基于公式（2），给出界面两侧介质的纵、横波速度与密度共六个地层参数，则可以通过矩阵求逆的方法计算PP波与PS波精确的反射系数．若对公式（2）中的六个地层参数进行组合，并且令λ=VP1/VS1、A=VP2/VP1、B=VS2/VS1、C=ρ2/ρ1，代入公式（2），可得

（3）

其中，α2=arcsin（Asinα1）、β1=arcsin（sinα1/λ）、β2=arcsin（Bsinα1/λ）．由公式（3）可以看出，纵波与转换横波反射系数的计算取决于四个组合变量λ、A、B、C；所以，若联合利用纵波与转换横波的反射系数反推地层参数，则需要建立四个方程，即

（4）

其中，fPP、fPS分别表示由公式（3）推出的纵波、转换横波的反射系数与λ、A、B、C的隐式关系，θ1、θ2为纵波与转换横波的入射角，即AVA道集的两个角度参数．

上述公式表明：用两个入射角地震道组成的道集进行AVA反演相当于四个方程解四个未知数，足够保证反演的可靠性．这两个地震道提取的反射系数可以通过将AVA道集的反射系数进行反距离加权平均法来获得，其公式如下：

R（θi）=

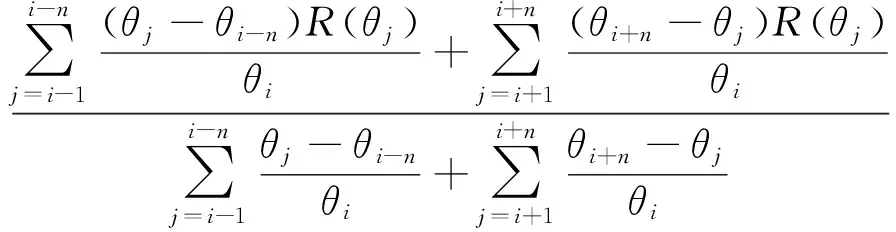
（5）

式中，下标i、j表示入射角序号．由于目前的转换横波处理水平有限，难以得到高信噪比的转换波叠前AVA道集；而平均入射角道集相当于把PP波与PS波的AVA道集的角度通过加权叠加减少为两个，信噪比会得到大幅度提高．为了保持PP波与PS波反射系数的变化趋势，这两个平均入射角要尽量差异大些．芦俊等（2011）的研究表明：在纵波速度与密度之间关系满足Gardner公式以及界面两侧地层的纵、横波速度变化率接近的情况下，PP波单独反演的最佳平均入射角为0°；PS波应选择中远偏移距入射角，考虑到地层的吸收衰减与动校正拉伸率的因素，30°平均入射角比较适合PS波的单独反演．但是在PP波与PS波的联合反演中，PP波叠加的优势振幅集中在中小偏移距，而PS波叠加的优势振幅集中在中大偏移距；所以0°与30°的平均入射角地震道无法同时适用于PP波与PS波的反演．由于PS波在0°入射角时的反射系数为0，联合反演应该选择非0°的小入射角，本文建议为5°．对于大入射角，折衷考虑到PP波在大入射角反射系数有可能较小，本文建议联合反演的大入射角选择为20°．在实际资料处理中，大、小平均入射角可以根据实际情况来选择．

为了验证通过反距离加权法得到的平均入射角地震道具有保幅性，我们建立了三种等效地层模型来进行数值模拟分析，模型参数如表1所示，界面类型包括：页岩/水饱和砂岩界面、页岩/气饱和砂岩界面与灰岩/气饱和砂岩界面．通过公式（2）计算精确的AVO曲线显示在图2中，分别用0°～10°与10°～30°的反射系数进行反距离加权来拟合5°与20°的平均反射系数，纵波与转换横波的反射系数平均值与理论值之间的差异如表2所示，可以看出：用公式（5）计算的反射系数平均值与理论值的误差最大为-1.57%，最小为0，完全能够满足平均入射角反演对反射系数精度的要求．

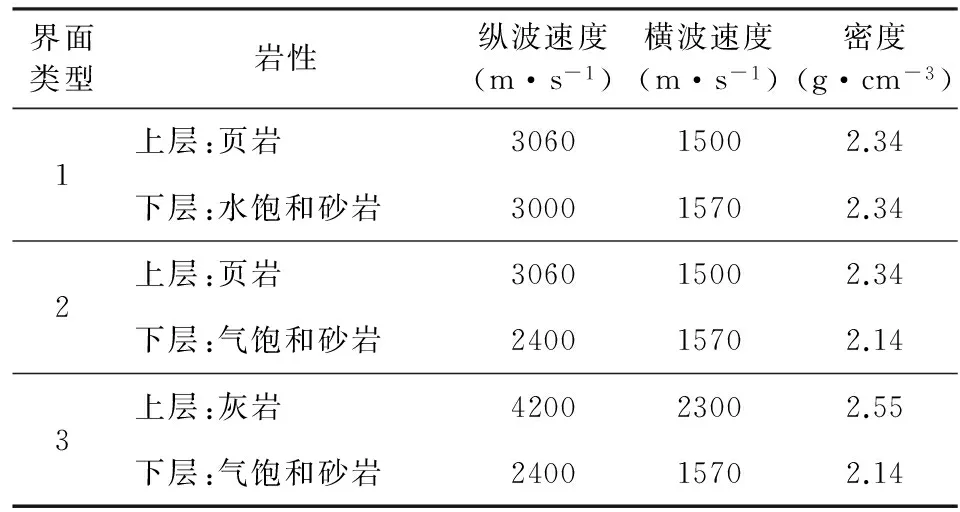
表1 三种含流体地层模型的弹性参数

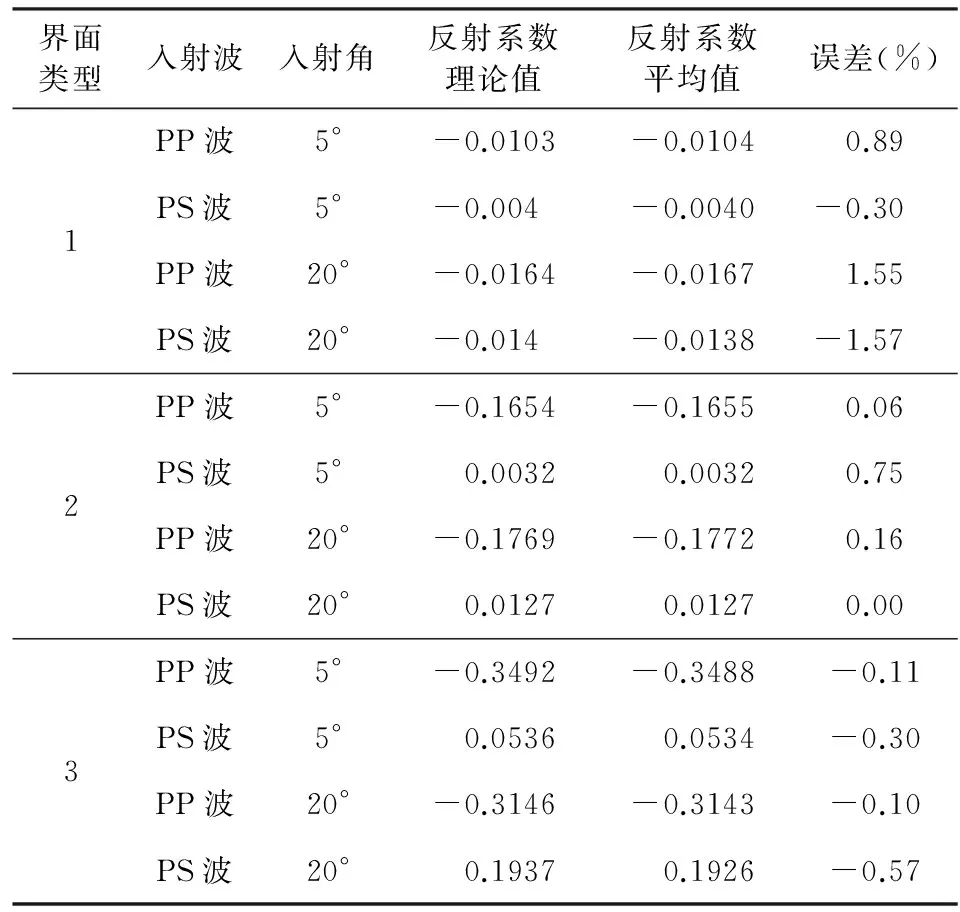
表2 三种界面的反射系数平均值与理论值的误差对比

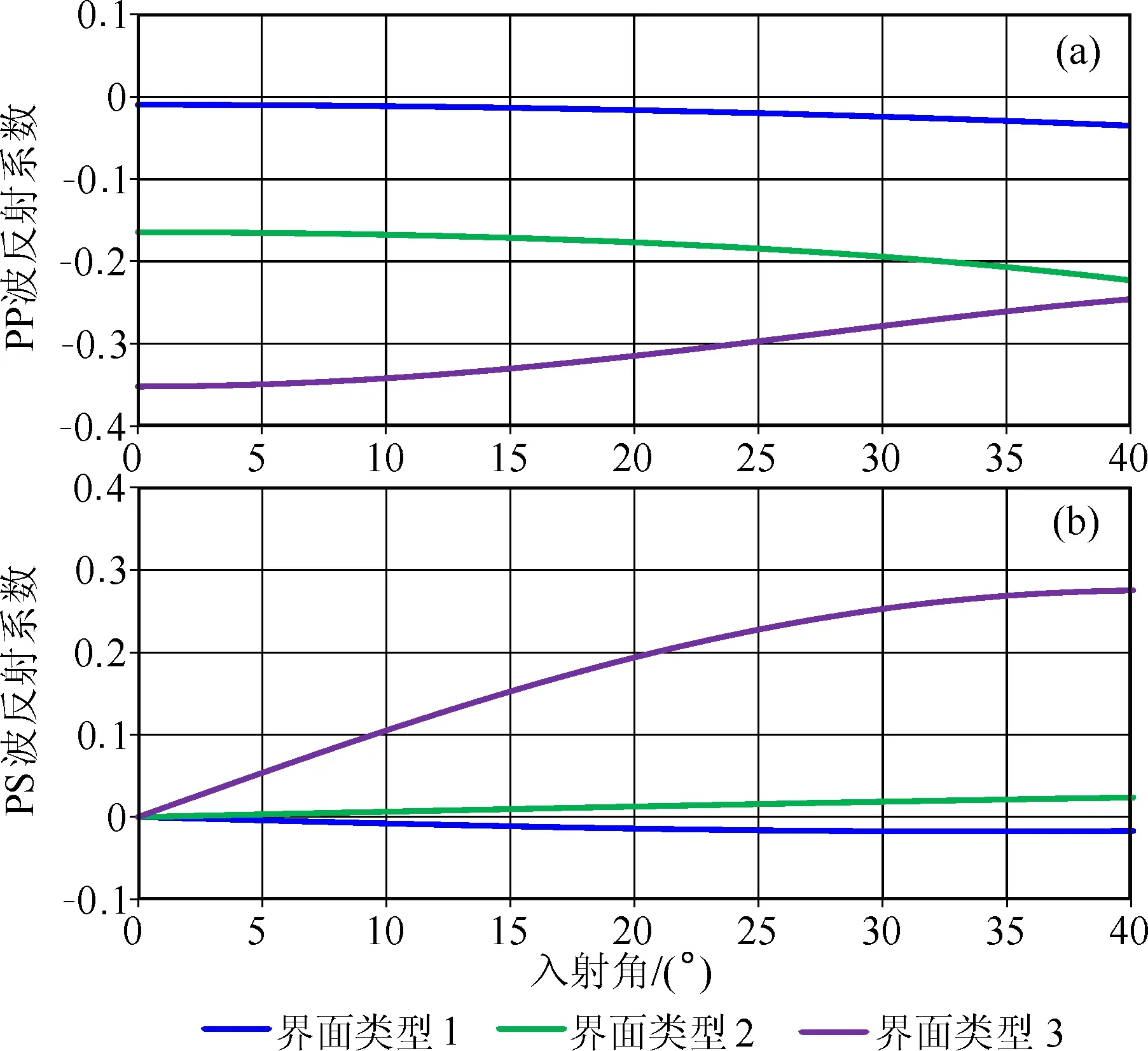
图2 通过Zoeppritz方程计算的精确AVO曲线

2.2 基于精确反射系数的最小二乘反演

平均入射角道集能够提高信噪比，同时提取的反射系数与理论值误差较小，在弹性阻抗反演或者是地层参数的直接反演中得到一定的应用（张宝金等，2002）．为了使得基于平均入射角道集的反演方法能够适用于更为广泛的地层条件，我们将基于Zoeppritz方程计算精确的反射系数来进行PP波与

PS波的联合反演，以提高反演的精度．通过最小二乘法建立的联合反演目标函数Q为Q（V）=‖WPP*RPP-DPP‖2+‖WPS*RPS-DPS‖2，

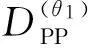
对PP波和PS波的反射系数向量在初始模型附近进行泰勒展开，统一的矩阵表述形式如下：

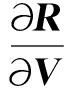
（7）

其中V0为纵波速度、横波速度和密度的初始猜测值组成的向量，ΔV为初始模型修正量．令雅各比矩阵G（V）=∂R/∂V，将公式（7）代入公式（6），可得：

Q（V）= ‖WPP*（RPP+GPPΔV）-DPP‖2

+‖WPS*（RPS+GPSΔV）-DPS‖2，

（8）

将公式（8）写成矩阵的展开形式为

为了使得目标函数Q（V）取值最小，要求存在∂Q（V）/∂ΔV=0，所以

（10）

进一步可求解ΔV为

（11）

将（11）式中的ΔV与初始的弹性参数向量V0进行向量求和，可得到更新后的初始模型，并进行上述过程的迭代；当目标函数Q（V）取值最小时，反演过程结束．更新后的弹性参数向量V0即为模型的反演结果．

在实际的联合反演中，输入的是由一系列采样点组成的时间序列，公式（11）中的向量需要进行扩展，以适用于时间序列模型的反演．扩展后的雅各比矩阵GPP与GPS具有如下统一形式：

（12）

公式（12）中的下标1，2，…，n表示不同的时间采样点，Ri表示第i个采样点位置的PP波或者PS波反射系数，∂Ri/∂Vj表示第i个采样点的PP波或者PS波的反射系数随第j个采样点的弹性参数变化量，并且有

（13）

在（13）式中，反射系数的求解必须由公式（2）进行线性方程组的数值求解；若用Aki-Richards反射系数近似公式建立公式（12）的雅各比矩阵，则本文的反演方法退化为基于Aki-Richards反射系数近似公式的反演方法．

为了在一次迭代中同时修改时间采样点的弹性参数，PS波的平均入射角道集必须和PP波在同一时间尺度上，所以必须把PS波道集压缩至PP波的时间上．该过程可以通过PP波与PS波的叠加剖面进行层位的对比解释，以获得不同层位的压缩系数，从而实现PS波的压缩．若同一地质界面的PP波与PS波反射波同相轴面貌差异太大，则需要工区内有足够多的测井合成记录来辅助完成层位的匹配．另外，地震子波需要在PS波平均入射角道集压缩至PP波时间后再提取，以保证地震子波时间尺度的一致性．由于PP与PS波的子波类型存在差异，所以PP波与PS波必须分别提取子波用于反演．

3 模型算例

我们建立了一个含有薄层的地层模型来验证本文的反演方法，模型参数如表3所示，其中第3层的厚度较薄，且与围岩的弹性参数差异较大，其顶、底界面均为强反差界面；其他的地层界面均为弱反差界面．合成记录是用射线追踪基于精确的反射系数模拟得到，PP波与PS波的地震子波分别设置为40 Hz以及30 Hz的雷克子波，采样率为1 ms；PS波的反射时间已经压缩至PP波时间上．AVA道集的最大入射角设置为25°，比较接近一般地震采集的入射角范围．

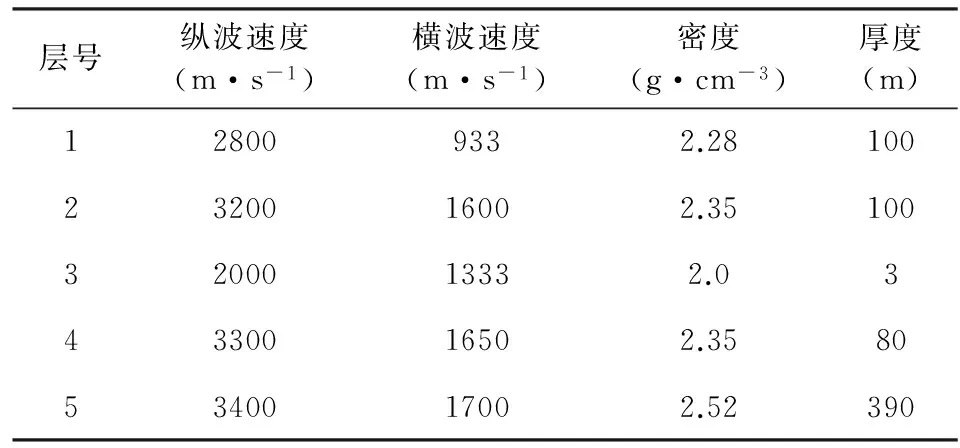
表3 理论模型参数

图3a、3c分别是PP波与PS波的AVA道集，图3b、3d分别由5°与20°入射角组成的PP波与PS波道集．图4为PP波与PS波的5°与20°角道集用本文方法反演得到的结果，可以看出：在初始模型没有任何界面变化的情况下，基于精确反射系数的反演方法能够获得与真实模型非常接近的反演结果；尤其是第3层的薄层，反演曲线在界面位置的突变与真实模型匹配较好．总体上看，与真实模型相比，该反演方法得到模型曲线在地层弹性参数突变的位置略有一些平滑，但是误差不大．图5是基于近似反射系数的反演结果，与图4对比可见：基于近似反射系数的反演没能很好地反映地层弹性参数的真实变化规律；即使在弱反差的界面上，其结果误差也较大，尤其是第2层的纵波速度反演结果明显偏小、密度明显偏大．从上述数值分析可以得出：即使在入射角范围较小的情况下，基于Zoeppritz方程精确反射系数的平均入射角道集PP波与PS波联合AVO反演的精度较高，能够适用于弹性参数反差较大、厚度较薄的地层参数反演．

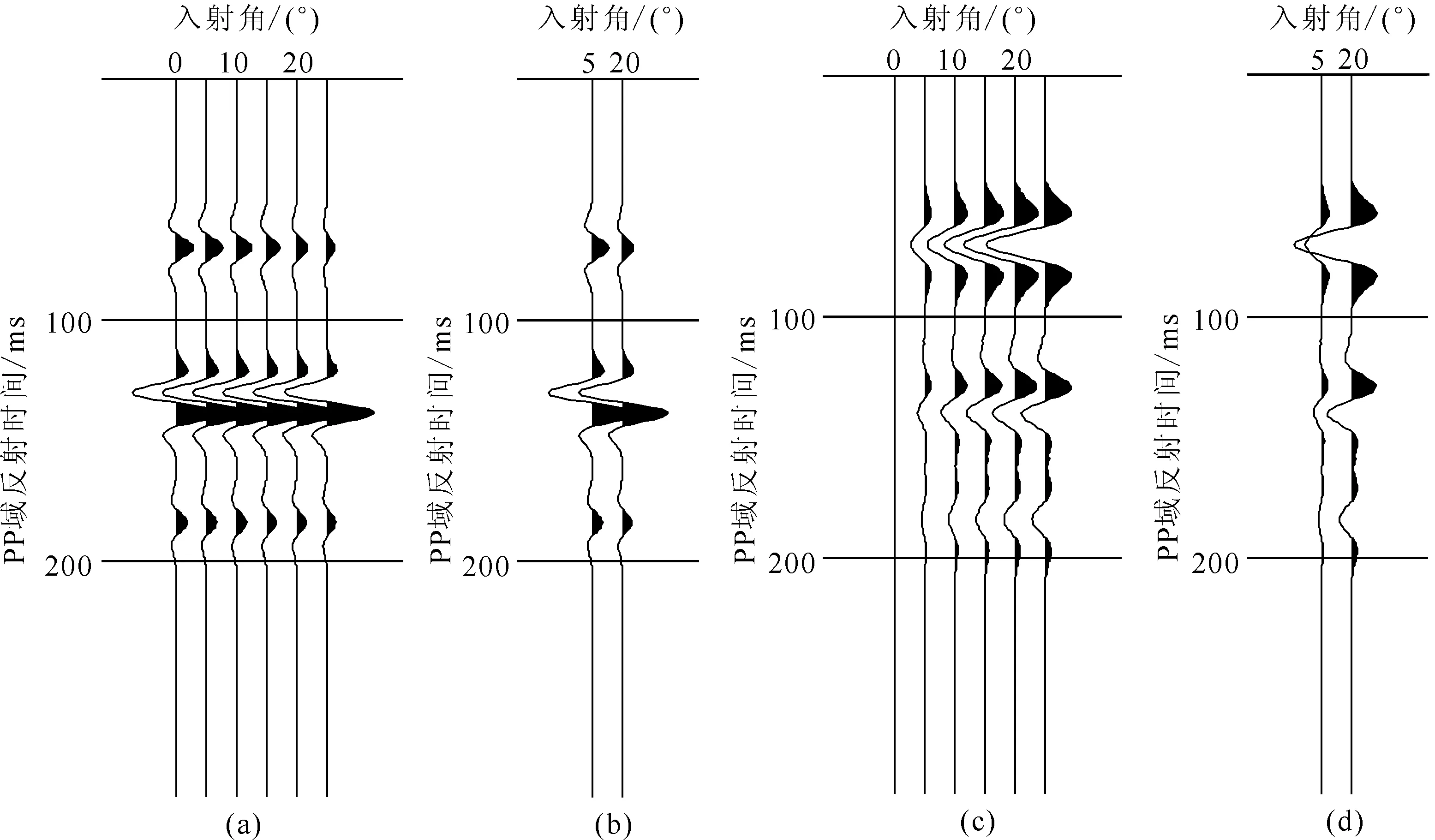
图3 PP波与PS波道集

在地震记录上加入20%的随机噪声后，测试噪声对本文反演方法的影响．如图6b、6d所示，5°与20°平均入射角地震道在加噪的AVA道集（图6a、6c）的基础上用入射角为0°～10°的地震道以及入射角为15°～25°的地震道分别加权叠加得到．用本文的反演方法分别对AVA道集以及平均入射角道集进行基于Zoeppritz方程精确反射系数的反演，如图7所示，平均入射角道集反演结果（蓝色曲线）与AVA道集反演结果（红色曲线）都很靠近真实模型（绿色曲线）；但是，红色曲线的噪声振幅强于蓝色曲线．所以，与AVA道集的直接反演相比，用平均入射角道集进行反演具有更强的抗噪性．

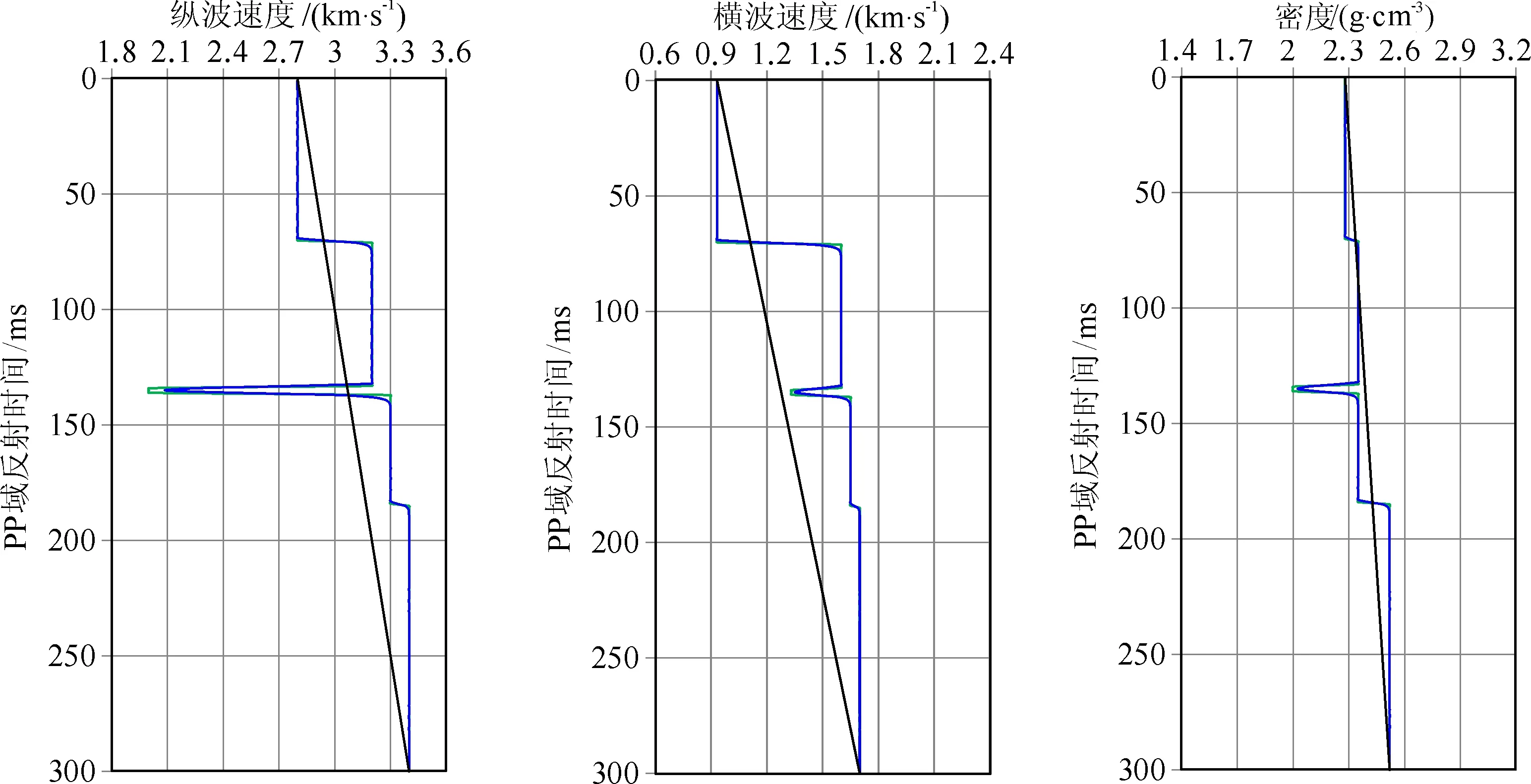
图4 基于Zoeppritz方程反射系数精确解的PP波与PS波平均入射角道集联合反演结果

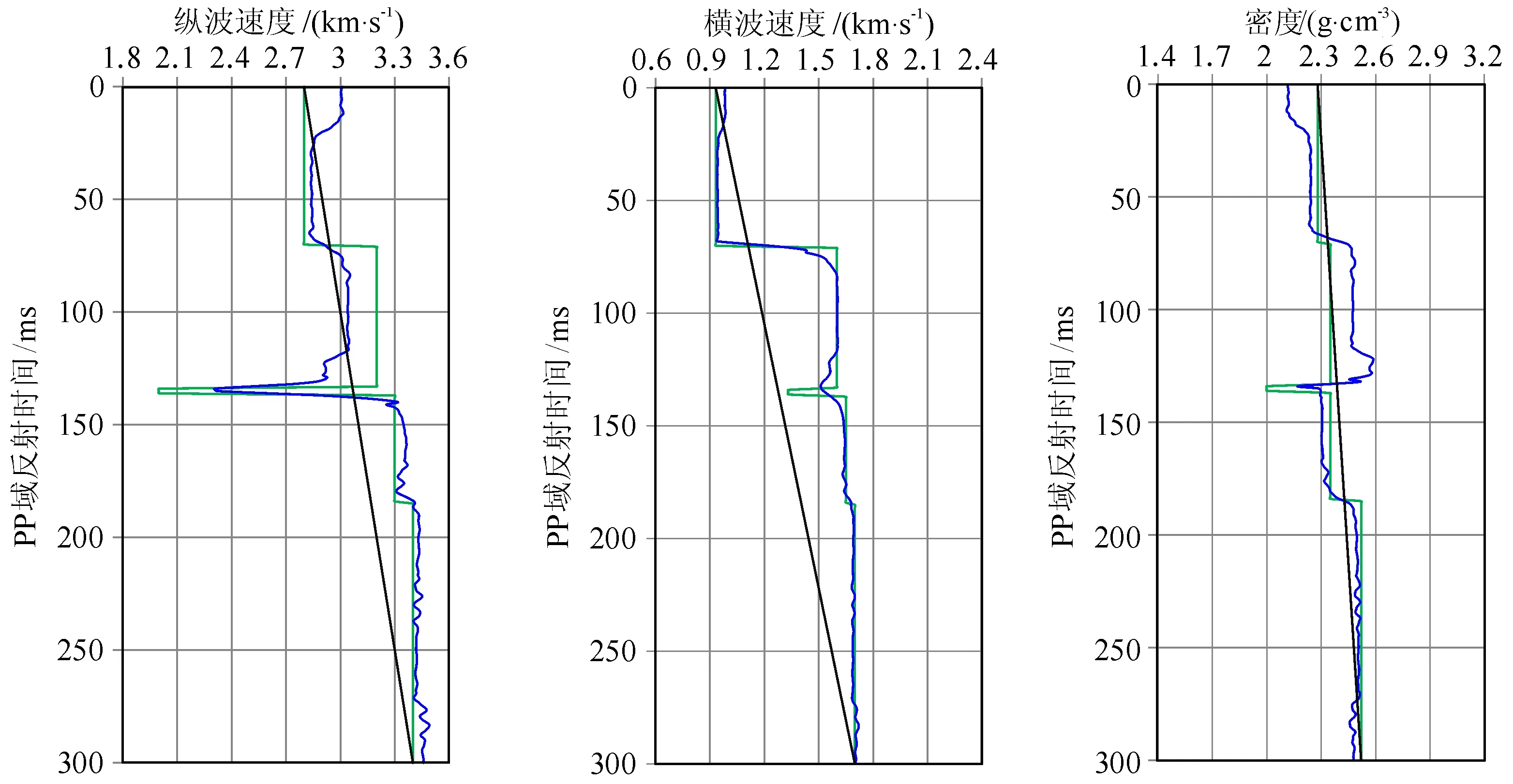
图5 基于Aki-Richards反射系数近似解的PP波与PS波平均入射角道集联合反演结果

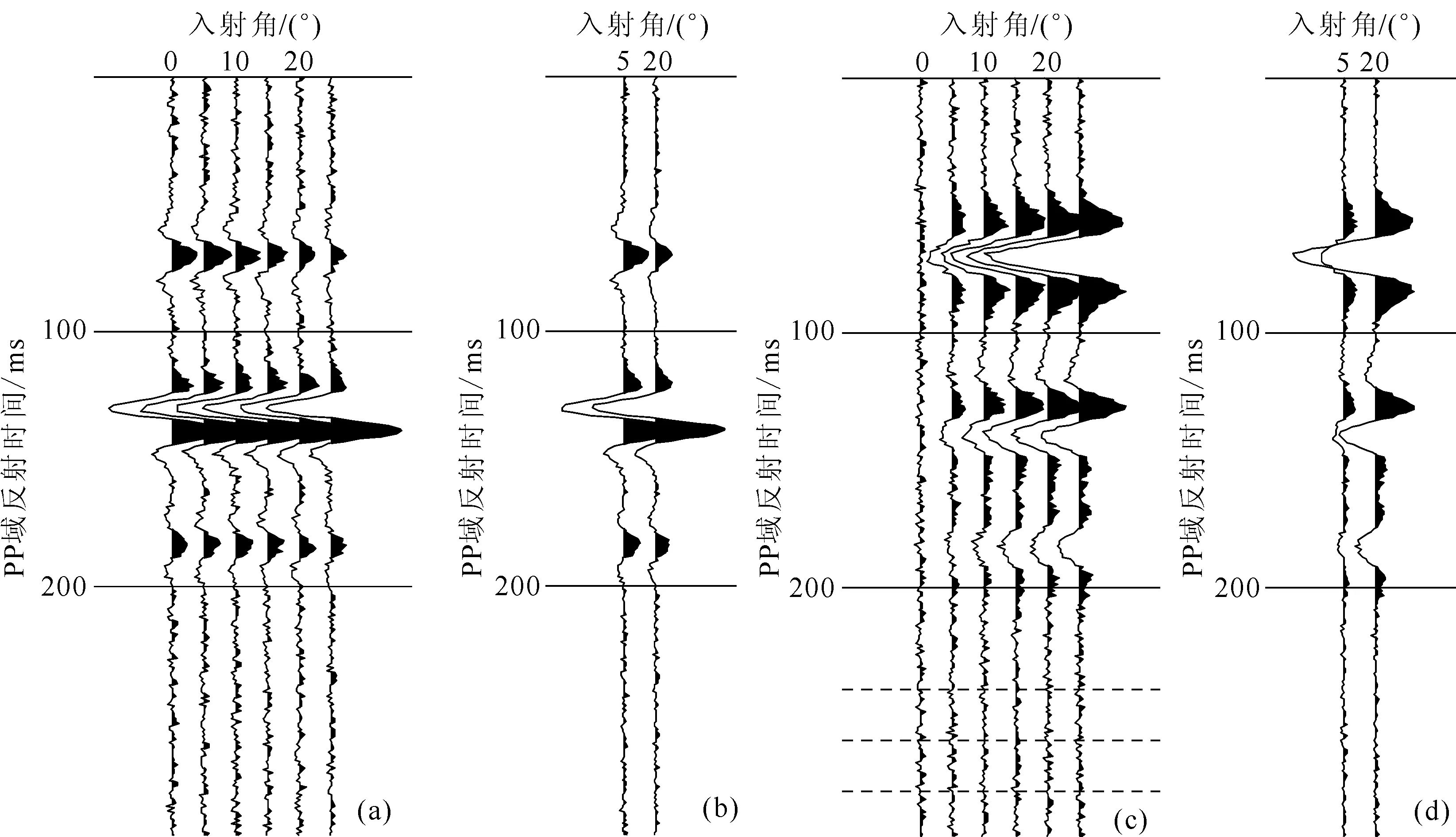
图6 加入20%的随机噪声后的PP波与PS波道集

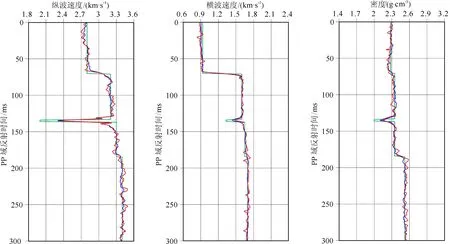
图7 在加入20%的随机噪声下，基于Zoeppritz方程反射系数精确解的PP波与PS波平均入射角道集与AVA道集联合反演的对比

4 实际数据的应用

实际数据的测试采用了淮南顾桥过井多分量地震数据，PP波与PS波道集的平均入射角选择为5°与20°，采样率为0.5 ms．该工区有实测的纵波速度曲线，横波速度曲线和密度曲线均是用经验公式将纵波速度曲线转换得到．沿着地震层位，这三条曲线通过外推得到了反演的初始模型，用测井合成记录标定了13-1煤、11-2煤以及8煤的PP波与PS波反射时间，同时将PS波的平均入射角道集压缩至PP波的反射时间上．

我们用基于Zoeppritz方程的精确反射系数对过井的一条测线上的PP波与PS波平均入射角道集进行了联合反演，得到了纵波速度、横波速度与密度剖面，分别如图8a、8b、8c所示，图中蓝色曲线为对应的测井曲线，该曲线上的白色线条标识了3个目标煤层的顶、底板位置．在反演剖面上，黑色表示地层的含碳量较高，一般为炭质泥岩或者煤岩；绿色向红色的过渡表示地层的岩性为泥岩-砂质泥岩-泥质砂岩-纯砂岩的岩性过渡．从图8可以看出，在测井位置上，本文提出的反演方法能够获得与测井模型非常接近的结果，三个目标煤层的顶、底界面的弹性参数突变较为清晰，煤层的展布容易识别．从三个弹性参数剖面上可以看出，有很多颜色相同的区域，如13-1煤与11-2煤之间红色区域覆盖范围相似，可以确定为砂岩；另外，一些区域的颜色区别较大，如13-1煤的顶板，在纵波与横波速度剖面上都表现为砂岩与泥岩的交替出现，但密度剖面上却表现为连续的砂体，此时则需要更多的地质资料对反演剖面解释结果进行标定．淮南顾桥煤矿已经对该工区的13-1煤进行了开采，验证资料表明：该工区13-1煤的顶板岩性确实为连续的砂岩，与密度剖面的解释结果吻合；但该区13-1煤顶板为河流沉积，导致其沉积相横向发生变化，可能引起了纵波速度与横波速度的横向变化（刘钦甫等，2004）．总体上看，本文方法提供了更多的弹性参数来进行对比解释，比单一剖面的解释具有更高的可靠性．

5 结论与认识

本文提出用平均入射角道集进行PP波与PS波的联合反演，并对该反演方法进行了理论模型与实际数据的测试，得到的结论与认识如下：

（1） 本反演方法基于Zoeppritz方程的精确反射系数进行弹性参数的直接反演，比基于近似反射系数的反演方法精度更高，具有更广泛的适用范围，能够解决一些强反差地层，如煤层、非固结砂岩地层等地层参数的反演问题．

（2） 平均入射角道集是由AVA道集进行反距离加权得到，其反射系数值与理论值之间的差异较小，并且具有良好的抗噪性；数值模拟结果表明，在低信噪比情况下，平均入射角道集的反演效果优于传统的AVA道集．

（3） 本反演方法是针对单界面模型的，所以较厚的地层参数反演结果比较精确；对于薄层，本文的反演方法也比基于近似反射系数的反演方法精度高，尤其是反演的结果能够较好反映薄层顶、底界面的位置；但是本反演方法得到的薄层弹性参数与真实模型相比略偏小，其原因是薄层的顶、底界面反射波会形成复合波，而本文的反演方法并未考虑波场调谐的问题．所以针对薄层的反演问题，应在后续的研究中考虑调谐作用对反射系数的影响．

Aki K I, Richards P G. 1980. Quantitative Seismology. San Francisco: W. H. Freeman & Co. Du Q Z, Yan H Z. 2013. PP and PS joint AVO inversion and fluid prediction.JournalofAppliedGeophysics, 90: 110-118,

Fatti J L, Smith G C, Vail P J, et al. 1994. Detection of gas in sandstone reservoirs using AVO analysis: A 3-D seismic case history using the Geostack technique.Geophysics, 59（9）: 1362-1376.

Hou D J, Liu Y, Hu G Q, et al. 2014. Prestack multiwave joint inversion for elastic moduli based on Bayesian theory.ChineseJ.Geophys. （in Chinese）, 57（4）: 1251-1264, doi: 10.6038/cjg20140422.

Li H, Dou Z L, Wang S X, et al. 2014. Seismic multi-attributes recognition for carbonate fractured-vuggy reservoirs with “weak reflection” characteristics.GeophysicalProspectingforPetroleum（in Chinese）, 53（6）: 713-719. Li J Y, Chen X H, Hao Z J, et al. 2005. A study on multiple time-lapse seismic AVO inversion.ChineseJ.Geophys. （in Chinese）, 48（4）: 902-908. Liu Q F, Liu H Q, Peng S P, et al. 2004. The roof geological features and stability of coal-bed No. 13-1 in Huainan coal-field.JournalofChinaCoalSociety（in Chinese）, 29（3）: 318-322.

Liu Y, Zhang J S, Hu G M, et al. 2012. Study of three-term non-Gaussian pre-stack inversion method.ChineseJ.Geophys. （in Chinese）, 55（1）: 269-276, doi: 10.6038/j.issn.0001-5733.

2012.01.026.

Lu J, Wang Y, Zhao W. 2010. Quantitative prediction of water content in porosity in coal measure strata using three-component seismic data.ChineseJ.Geophys. （in Chinese）, 53（7）: 1734-1740, doi: 10.3969/j.issn.0001-5733.2010.07.025.

Lu J, Wang Y, Shi Y. 2011. Coal hardness prediction using joint inversion of multi-wave seismic data and logging.ChineseJ.Geophys. （in Chinese）, 54（11）: 2967-2972, doi: 10.3969/j.issn.0001-5733.2011.11.027.

Qian R J. 1993. Accompanying and secondary events in seismic time section.OilGeophysicalProspecting（in Chinese）, 28（3）: 282-291.

Shuey R T. 1985. A simplification of the Zoeppritz equations.Geophysics, 50（4）: 609-614.

Smith G C, Gidlow P M. 1987. Weighted stacking for rock property estimation and detection of gas.GeophysicalProspecting, 35（9）: 993-1014.

Stewart R R. 1990. Joint P and P-SV inversion. CREWES Research Report 2.

Veire H H, Landrø M. 2006. Simultaneous inversion of PP and PS seismic data.Geophysics, 71（3）: R1-R10.

Wang Y H. 1999. Approximations to the Zoeppritz equations and their use in AVO analysis.Geophysics, 64（6）: 1920-1927.

Xu S H, Han L G, Guo J. 2012. Multiwave inversion of anisotropic parameter and PS wave AVO analysis in TTI media.ChineseJ.Geophys. （in Chinese）, 55（2）: 569-576, doi: 10.6038/j.issn.0001-5733.2012.02.019.

Yin X Y, Cui W, Zong Z Y, et al. 2014. Petrophysical property inversion of reservoirs based on elastic impedance.ChineseJ.Geophys. （in Chinese）, 57（12）: 4132-4140, doi: 10.6038/cjg20141224.

Zhang B J, Cheng G, Cao J Z, et al. 2002. Calculating the zero offset P and S reflection using the none-zero offset P-P and P-SV wave.ProgressinGeophysics（in Chinese）, 17（1）: 102-106.

Zhang G Z, Du B Y, Li H S, et al. 2014. The method of joint pre-stack inversion of PP and P-SV waves in shale gas reservoirs.ChineseJ.Geophys. （in Chinese）, 57（12）: 4141-4149, doi: 10.6038/cjg20141225.

Zhang Y G, Wang Y, Wang M Y. 2004. Some key problems in the multi-component seismic exploration.ChineseJ.Geophys. （in Chinese）, 47（1）: 151-155.

Zhao B, Wang Y, Lu J. 2012. Recent advances of multi-component seismic and some of its key issues.OilGeophysicalProspecting（in Chinese）, 47（3）: 506-516, doi: 10.13810/j.cnki.issn.000-7210.012.3.24.

Zheng X D. 1991. Approximation of Zoeppritz equation and its

application.OilGeophysicalProspecting（in Chinese）, 26（2）: 129-144. Zhi L X, Chen S Q, Li X Y. 2013. Joint AVO Inversion of PP and PS waves using exact Zoeppritz equation.∥83rd Annual International Meeting, SEG, Expanded Abstracts, 457-461.

附中文参考文献

侯栋甲, 刘洋, 胡国庆等. 2014. 基于贝叶斯理论的叠前多波联合反演弹性模量方法. 地球物理学报, 57（4）: 1251-1264, doi: 10.6038/cjg20140422.

李弘, 窦之林, 王世星等. 2014. 碳酸盐岩缝洞型储层“弱反射”特征的地震多属性识别. 石油物探, 53（6）: 713-719.

李景叶, 陈小宏, 郝振江等. 2005. 多波时移地震AVO反演研究. 地球物理学报, 48（4）: 902-908.

刘钦甫, 刘衡秋, 彭苏萍等. 2004. 淮南煤田13-1煤层顶板地质特征与稳定性研究. 煤炭学报, 29（3）: 318-322.

刘洋, 张家树, 胡光岷等. 2012. 叠前三参数非高斯反演方法研究. 地球物理学报, 55（1）: 269-276, doi: 10.6038/j. issn.0001-5733.2012.01.026. 芦俊, 王赟, 赵伟. 2010. 应用三分量地震数据反演煤系地层孔隙含水量. 地球物理学报, 53（7）: 1734-1740, doi: 10.3969/j.issn.0001-5733.2010.07.025.

芦俊, 王赟, 石瑛. 2011. 利用多波地震与测井数据联合反演预测煤岩的坚固性. 地球物理学报, 54（11）: 2967-2972, doi: 10.3969/j.issn.0001-5733.2011.11.027.

钱荣钧. 1993. 地震时间剖面上的伴随相位和次生相位. 石油地球物理勘探, 28（3）: 282-291.

徐善辉, 韩立国, 郭建. 2012. TTI介质各向异性参数多波反演与PS波AVO分析. 地球物理学报, 55（2）: 569-576, doi: 10.6038/j.issn.0001-5733.2012.02.019.

印兴耀, 崔维, 宗兆云等. 2014. 基于弹性阻抗的储层物性参数预测方法. 地球物理学报, 57（12）: 4132-4140, doi: 10.6038/cjg20141224.

张宝金, 成谷, 曹景忠等. 2002. 用非零偏P-P波、P-SV波计算零偏反射纵波和反射横波. 地球物理学进展, 17（1）: 102-106.

张广智, 杜炳毅, 李海山等. 2014. 页岩气储层纵横波叠前联合反演方法. 地球物理学报, 57（12）: 4141-4149, doi: 10.6038/cjg20141225.

张永刚, 王赟, 王妙月. 2004. 目前多分量地震勘探中的几个关键问题. 地球物理学报, 47（1）: 151-155.

赵波, 王赟, 芦俊. 2012. 多分量地震勘探技术新进展及关键问题探讨. 石油地球物理勘探, 47（3）: 506-516, doi: 10.13810/j.cnki.issn.1000-7210.2012.03.024.

郑晓东. 1991. Zoeppritz方程的近似及其应用. 石油地球物理勘探, 26（2）: 129-144.

（本文编辑 何燕）

Joint PP- and PS-wave inversion of gathers with average incident angles

SHI Ying1， LU Jun1*， YANG Zhen1， YANG Chun2

1SchoolofEnergyResources,KeyLaboratoryofMarineReservoirEvolutionandHydrocarbonAccumulationMechanism，MinistryofEducation，ChinaUniversityofGeosciences，Beijing100083，China2SchoolofGeophysicsandInformationTechnology，ChinaUniversityofGeosciences，Beijing100083，China

To coal reservoirs, the AVO method is not widely applied. The main reason for this phenomenon is that the offset is not large enough to provide wide incident angles for the inversion and the elastic parameters are hard-contrast at the top and bottom interface of the coal seam. Therefore, the conventional inversion method based on Aki-Richard equations is not applicable. To solve this problem, we propose a joint PP- and PS-wave inversion method based on the exact Zoeppritz equations, which can invert gathers of PP- and PS-waves with average incident angles.An average incident gather consists of two incident angle traces of PP- and PS-waves. The small and large incident angle traces are derived by weighted stacking PP- or PS-wave AVA gathers in the areas with relatively smaller and larger angles, respectively. We deduce the formula about the average reflection coefficients and the four combined variables of the elastic parameters, which shows that the strata elastic parameters can be inverted by PP and PS reflection coefficient equations at two average incident angles. We use three types of strata models with fluid to compare the average and theoretical reflection coefficients. It is shown that both the PP and PS average reflection coefficients are high-precision events after weighted stacking.We establish the target function for the joint inversion by the least square method. Compared to the conventional inversion method, the initial model input for the inversion does not need to be precise. We use the exact Zoeppritz equations to calculate PP and PS reflection coefficients during the forward modeling and adopt the first-order approximations during solving the model updating variations. We test the inversion method on the model consisting of a hard-contrast thin coal seam. The initial model is linear without any interface and the synthetic records are noisy, however the performance of the inversion is satisfied. We apply the inversion method to the field data. In the situation that the offset area is limited, the inversion method can invert the elastic parameters about the coal measure strata with high resolution. It is easy to identify the top and bottom interfaces of the target coal seams in the inversion results. The inversion method provides a new idea for seismic surveys in complex reservoirs.

Average incident angle; Joint inversion; PS-wave; Reflection coefficient; Least squares

中央高校基本科研业务费专项资金（2652013093）、北京高等学校青年英才计划项目（YETP0661）、国家高技术研究发展计划（863计划）课题（2013AA064201）和国家自然科学基金项目（41574126，41425017）资助．

石瑛，女，博士后，从事多分量地震解释与反演的研究．E-mail：quartzsy@163.com

*通讯作者 芦俊，男，副教授，主要从事多分量地震技术的研究工作．E-mail：lujun615@163.com

10.6038/cjg20151223

P631

2015-04-24，2015-12-01收修定稿

10.1016/j. jappgeo.2013.01.005.

石瑛， 芦俊， 杨震等. 2015. 平均入射角道集PP波与PS波联合反演.地球物理学报，58（12）:4617-4627,doi:10.6038/cjg20151223.

Shi Y, Lu J, Yang Z, et al. 2015. Joint PP- and PS-wave inversion of gathers with average incident angles.ChineseJ.Geophys. （in Chinese）,58（12）:4617-4627,doi:10.6038/cjg20151223.