金属矿山地地区地震勘探随机噪声的波动方程模拟
李光辉, 李月
吉林大学信息工程系, 长春 130012
金属矿山地地区地震勘探随机噪声的波动方程模拟
李光辉, 李月*
吉林大学信息工程系, 长春 130012
消减随机噪声是目前陆地地震勘探数据处理的关键问题之一,分析随机噪声的产生机制及特征是对其进行有效压制的先决条件.本文针对中国南方山地金属矿区的勘探环境,根据随机噪声中包含的自然噪声和人文噪声的发声机理分别确定其噪声源函数,以波动方程作为噪声传播模型对山地地区随机噪声进行建模,将随机噪声作为一个综合波场,并且与实际噪声记录进行比较.随机噪声记录作为时空域的二维随机过程,分别对模拟噪声和实际噪声记录的时间域波形(振动图)特征包括频谱、功率谱密度,相空间轨迹图,统计量特征(能量分布,累积分布,均值,方差,峰度,偏度),和空间域波形(波剖面)特征包括波数谱和统计量特征进行比较,对比结果显示在时空域模拟噪声和实际噪声都有基本相同的性质,证明了本文对随机噪声模拟方法的可行性,为进一步研究随机噪声时空域传播特性以及噪声消除奠定理论基础.
金属矿地震勘探; 随机噪声; 波动方程; 波场模拟
1 引言
地震勘探方法是资源勘探的主要手段之一,它以人工激发的弹性波在地层中的传播为研究基础.随着国家对矿产资源需求量的增多,以及易探、易采资源的减少,从事勘探理论与应用研究的难度越来越大.在陆地地震勘探数据采集过程中,勘探目标越深、越薄、越不规则,对地震记录质量的提高要求越大.随机噪声是严重影响地震记录信噪比的因素,由于无规律性,给地震资料的处理带来很大的困难,为此人们不断提出、改进消噪方法去除随机噪声,提高地震资料的信噪比(Wu and Yang, 2011;李月等,2013;Liu et al., 2013; Tian et al., 2014).其中对随机噪声的了解和认识是压制随机噪声的首要问题,人们通过不同环境下的地震噪声记录,对噪声特征值进行分析,了解各种干扰产生的原因及其特性,寻找规律性(Young et al.,1996; Bonnefoy-Claudet et al., 2006; Barajas-Olade and Ramadan, 2011; 朱良保和王清东,2011; 赵盼盼等,2012;鲁来玉等,2014; McNamara and Buland, 2004;潘佳铁等,2014),并提出压制方法.至今为止,对随机噪声的进行定性定量地分析还比较少.
随机噪声根据其噪声源类型分为自然噪声和人文噪声(Bonnefoy-Claudet et al., 2006b):自然噪声是指自然因素产生的噪声,例如风吹过时,风对地面的作用,植被枝叶的拍打声,植被随风摆动、高大建筑物抖动引起的地面微震等(Ward and Crawford, 1966).这里将由风引起的噪声统称为风成噪声.若采集地点临近海、河流时,还有海浪拍打海岸,河水流动引起的地面震动;另外还有大规模气候变化、火山爆发等引起的远源微震.人文噪声是指人类活动引起的噪声,例如人类居住活动、工厂运作、交通噪声,以及检波器附近机器开动,人、动物走动引起的震动等等.随机噪声是一个时空域二维的随机过程,山地地区地形复杂,植被覆盖率高,给地震数据的采集带来很大的干扰,本文结合山地地区实际数据采集情况对噪声源进行模拟,用波动方程描述传播过程,将随机噪声作为各个噪声源的叠加波场,对山地地区随机噪声进行建模,并与实际噪声的时空域特征进行对比,时域波形特征包括频谱,功率谱密度,相轨迹图,统计量特征(均值,方差,能量分布,累积分布,峰度,偏度);空域波形特征包括波数谱及统计量特征.通过建立金属矿山地地区地震勘探随机噪声的理论模型,为进一步研究随机噪声的时空域传播特性以及选择合适的噪声压制方法提供理论指导作用.
2 山地地区随机噪声模拟
随机噪声由风吹草动、海浪、雷电、开动的机器、人车行走等外力产生的,其特性取决于当地的地质、地理、气象等因素以及接收点周边的环境.根据前人研究总结随机噪声中各类噪声频率分布范围如图1所示.自然噪声中,由气候变化,季风引起的地壳运动,雷电、海洋、火山爆发等引起的微震幅度微小,因此只考虑由风作用引起的各类干扰.
与非山地地区相比,山地地区地形复杂,植被覆盖情况高,尽管自然噪声源的种类大致相同,但是由于地形对风的影响导致山地地区风噪声的性质与非山地地区不尽相同.下面的章节中分别对风对地表和树木的作用力这两类噪声的源函数进行模拟,并通过波动方程对随机噪声进行建模.随机噪声是一系列噪声的叠加结果,假设噪声源以点源的形式分布在接收装置周围,如图2.
2.1 自然噪声
假设地表是均匀、各向同性的半无限大弹性介质,风吹过地表时风荷载对地表的作用力引起地表发生形变(Sorrells et al., 1971),风荷载对树木的作用力导致树木发生振动引起的地面抖动以及风吹过时枝叶摆动发出的声音耦合到地面被接收装置检测到(Young et al.,1996; McNamara and Buland, 2004).

Fig.1 随机噪声频率范围分布

Fig.2 各类噪声点源分布示意图
2.1.1 风对地表的作用力引起的噪声
在风振理论中,风速可以看成是平均风速和脉动风速的和(王之宏,1994),表达式为
(1)

平均风速随高度和地表粗糙度呈指数变化(王之宏,1994),表达式为
(2)

脉动风速谱采用风振理论中广泛使用的Davenport风速谱(Davenport, 1961),表达式为

(3)
S(ω)为脉动风速谱,ω为脉动风角频率,为湍流积分尺度系数且=,K为地表拖拽力系数,B类地区K=0.0022.
由式(3),根据Shinozuka声振动理论(Shinozaka and Jan, 1972),脉动风速时域波形为
(4)
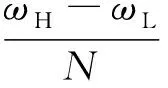
式(4)是平地脉动风速的表达式,适用于非山地地区风干扰模拟,而山地地区风速还受到山体的影响.山体对风速的影响很大,通常采用一个无量纲参数——加速效应来具体描述,加速效应(speed-upeffect) 指在山地地形中,某高地平均风速比平均相应高度平均风速有所增加的效应,一般来说在山顶的近地面加速效应最为明显.山体对风速影响的水平距离,一般在向风面为山高的5~10倍,背风面为15倍.山脊越高,坡度越缓,在背风面影响的距离越远.对于山体形状的模拟,主要有三角形、钟形、高斯型、余弦平方形和余弦形等(李鑫, 2010).不同的山体形状,对于加速效应的影响不同,考虑到山地的复杂性可取各种模型结果的平均值或者用某一种山体模型进行研究.

Fig.3 余弦山体形状示意图
本文采用余弦山体模型(图3),模型函数为
zm=H×[1+cos(πr/2L1)]/2,
(5)

加速效应通常用一个无量纲的参数来定量描述,即加速比为

(6)
式中U(z)表示山地地面以上z高度处的平均风速,U0(z)表示平面地面以上z高度处的平均风速.
Taylor和Lee(TaylorandLee, 1984)提出的“初始算法”(“originalGuidelines”)是通过ΔSmax计算不同高度处计算不同高度处的ΔS,公式为
ΔSmax=BH/L1,
(7)
ΔS=ΔSmaxexp(-Az/L1),
(8)
其中A和B是两个经验常数,根据山体的几何条件而有所不同,但未考虑地面粗糙度等其他因素的不同,当山体为二维连续时,A=3.5,B=1.55(李鑫, 2010).
由式(2)可知,平均风速随高度和地表粗糙度呈指数变化,脉动风速均方根值在山体不同位置的分布规律与平均风速分布规律基本一致.定义脉动风速均方根的增大比ΔSσ为(李鑫, 2010)

(9)
σ(z)为山地风场脉动风速均方根值,σ0(z)为平均风场脉动风速均方根值.
由于不同坡度山体背风面山脚的脉动风速均方根增大最大值均出现在0.8H处,坡度越大,脉动风速均方根增大值越大,在0.8H上下均大体呈直线分布.根据以上特点,建立了三折线型模型为(孙毅等,2011)
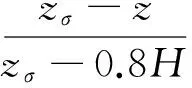
ΔSσ(z)=0,z>zσ,
(10)ΔSσ max为0.8H处的脉动风均方根最大增大值,zσ为山体影响高度,表达式为
ΔSσ max=-0.96+3.05H/L1,
(11)
zσ=1.62H.
(12)
山地地区脉动风速谱在垂向坐标上有较大差异,根据Kolmogrov理论(冯宏等,2013),频域内脉动风速功率谱为
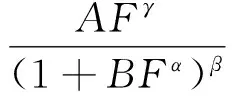
(13)
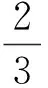
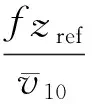
S(z,f)为山地脉动风速功率谱表达式,由脉动风压谱的概念及Weiner-Khintchine定理得到脉动风压功率谱为
Sp(z,f)=ρ2U(z)S(z,f),
(14)
Sp为脉动风压谱,ρ为空气密度,U(z)为z高度处的平均风速,S(z,f)为脉动风速谱.
根据式(4)的理论得到山地地区脉动风压的时域波形为
(15)
各参数定义同上.
风压是平均风压和脉动风压的和,公式为
(16)



Fig.5 风吹过地表时引起的噪声单道(No.9)波形
2.1.2 树木振动引起的噪声
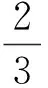

(17)
式中CD分别为拖曳力系数,ρ为空气密度,v为风速,S为受力面积.
式中CD=0.013,由于树冠受力面积远大于树干的受力面积,因此只考虑树冠的受力作用,风对树冠的总作用力为:WP=CA×Fd.下面对树木进行一些条件假设(Bourg, 2002; 王琳, 2006):
(1)将树干简化为直径随高度按幂函数变化的弹性杆,弹性杆长度为l,为地面到树冠中心的高度.

(4)树干为均质,密度大小为ρt.
(6)此弹性杆初始倾斜角度为θ.
根据上面给出的6条假设,把树干简化为一端固定,自由端有集中质量团的变截面弹性杆,得到树干的力学模型如图6b所示.对树木的力学模型进行分析,考虑到一端固定一端有集中质量的弹性杆边界条件,可以得到弹性杆振动方程,用y(x,t)表示弹性杆的振动响应,由经典的梁的横向振动理论,对于一般的变截面梁,横向自由振动方程为
0≤x≤l,
(18)
E为树干弹性模量,t为时间.
方程 (18)的边界条件为


(19)
初始条件为

(20)

在风荷载作用下,树的振动响应主要是受迫振动响应.梁的受迫振动方程为
0≤x≤l,
(21)
边界条件,初始条件同式(19)、(20),本文均为零.


Fig.6 (a) 树木的简化模型; (b) 树木的力学模型
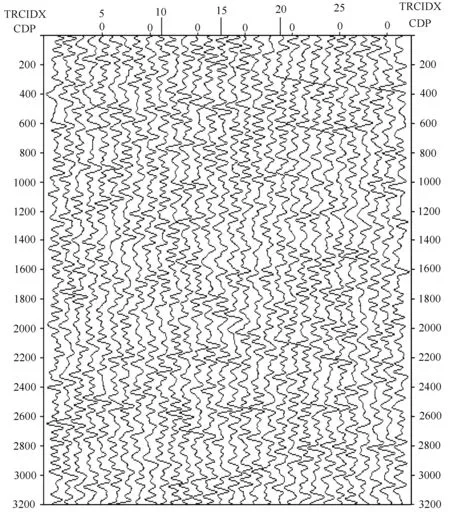
Fig.7 树木风振引起的噪声记录
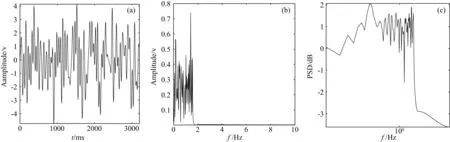
Fig.8 树木振动引起的噪声单道(No.5)波形
2.1.3 风吹树木发出的声音引起的噪声
在风荷载作用下,除了引起树木振动导致的噪声,还有枝叶在风中摆动发出的声音导致的噪声.在气动声学理论中,气流流过障碍物时,由于空气的黏滞性,在障碍物背面产生气流涡流诱发的气动噪声,例如生活中常听到的风吹过电线时发出的声音,风吹过树枝、树叶时发出的声音等,如图9所示.
Lighthill声相似原理就是通过模拟发声源类比气流噪声,其原理图如图10.风速是平均风速和脉动风速的和,平均风对障碍物产生静态荷载,并不会产生气动噪声,脉动风作为随时间变化的随机变量,对障碍物产生脉动风荷载,Lighthill类比就是将这部分脉动压力用一系列声源代替,如同障碍物表面放置了一系列的噪声源,能发出与脉动风压诱发的大小一样的气动噪声(张强, 2012).物体在流体中的发声问题满足FfowcsWilliams-Hawkings方程(简称FW-H方程) (WilliamsandHawkings, 1969):

Fig.9 风吹过障碍物时气动噪声产生示意图
(22)

方程(22)中,右边第一项是Lighthill声源项,为四极子声源项,第二项表示由表面脉动压力引起的声源(力分布),是偶极子声源项,第三项表示由加速度引起的声源(流体位移分布),是单极子声源项.通过式(17)将气流运动与声压联系起来.本文风吹树木发出的声音是由偶极子声源引起的,方程(22)右边其余两项均为零.单极子声源是构成其他两种声源的基础,是指媒质中流入的质量或热量不均匀时形成的声源(或叫简单声源),单极子声源如调制气流声源(语气声,气流扬声器),脉冲喷气等.单极子和脉动球体一样,声能量均匀的向各个方向辐射,如图11a所示(Russelletal., 1999).单极子声源强度定义为

Fig.10 Lighthill 声相似原理示意图
Q=4πa2U,
(23)
式中a为单极子声源的半径,U为表面振动速度,这里取脉动风速.
通过求解与方程(29)类似的无限大空间内的声波波动方程,可以得到声强为Q时的声压为
(24)
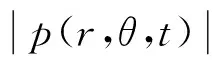
偶极子声源是指当流体中有障碍物存在时,流体与物体产生的不稳定的反作用力形成的.偶极子声源是强度相同,方向相反的两个单极子声源组成,满足kd≪1,k是波数,d是两个单极子声源之间的距离,偶极子声源是力声源,如图12a所示.
通过求解无限大空间内的声波波动方程,得到偶极子声源辐射声压为
(25)

采用树的简化模型,当有风吹过树冠时,由于树枝树叶受力面积的大小不同,产生了不同频率范围的风吹声,满足
fw=0.2V/L,
(26)

Fig.11 (a) 单极子声源辐射,(b) 单极子声源指向性

Fig.12 (a) 偶极子声源, (b) 偶极子声源指向性
式中fw为风吹声的频率,V为物体在流体中的运动速度,这里指风速,L为物体的特征长度,可以看出,风速越大,树枝、树叶越细,越小,风吹声的频率就越大.


Fig.13 风吹树木引起的气流噪声记录

Fig.14 风吹树木引起的气流噪声单道(No.19)波形
2.2 人文噪声人文噪声主要是由人类活动引起的噪声,根据噪声源与接收点的距离大致上分为近场噪声和远场噪声.
2.2.1 近场噪声

(27)式中A为幅值,bw为相对带宽,t为时间变量,τ为时延,fc为中心频率,ζ为初始相位.
式(27)为波动方程(29)的噪声源函数,通过求解波动方程后将所有的解叠加得到近场人文噪声记录(图15),单道时域波形及其谱特征(图16),可以看出近场人文噪声频谱范围较窄,主要能量集中在20Hz以内,正如图1中描述的人车走动等干扰的分布范围.
2.2.2 远场噪声
远场噪声是采集区远处由于人类居住活动、交通、工厂等产生的噪声,远场噪声是宽频带(0~200Hz以上)的平稳随机噪声,可由多个(理论上是无穷多个)不同周期不同随机初相位的简谐波叠加而成(McNamaraandBuland, 2004),点源分布如图2中加号所示.
远场噪声点源震源函数表达式为
x(t)=ajcos(kjxj-ωit+εj),
(28)
j为第j个分量,a为幅值,k为角频率,ω为角频率,ε为初始相位,x为距离,t为时间变量.
远场噪声源与接收点装置的相对位置比较稳定,可近似为不随距离变化,只随时间变化的源函数,因此xl=0.将式(28)作为波动方程的源函数,得出波动方程的解并将一系列不同频率不同初始相位的解叠加得到远场人文噪声记录如图17,单道波形及其谱特征如图18,远场噪声幅值较小,频谱范围较宽,符合图1中所示的人文噪声频率范围.

Fig.15 近场人文噪声记录
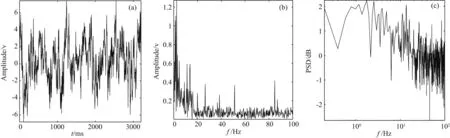
Fig.16 近场人文噪声单道(No.8)波形

Fig.17 远场人文噪声记录

Fig.18 远场人文噪声单道(No.23)波形

Fig.19 山地地区随机噪声记录对比(a) 实际噪声; (b) 模拟噪声.

Fig.20 单道(No.6)波形对比

Fig.21 相轨迹图
3 结果对比
上述模拟了山地地区各类噪声源引起的噪声进行模拟,这里主要将模拟噪声和实际噪声的特征进行对比,实际噪声与模拟噪声记录如图19a和b所示,可以看出模拟噪声和实际噪声记录基本相似.随机噪声作为时空域的二维随机变量,是噪声源通过波动方程传播的综合波场,因此将时间域(振动图)和空间域(剖面图)的特征逐一进行对比,以证明对随机噪声建模方法的有效性.
3.1 振动图特征对比
振动图特征除了频谱和功率谱密度,还包括混沌性和统计量特征(包括均值、方差、峰度、偏度、频率分布以及累积分布).分别从图19a、b中抽取任意相同道,文中抽取第6道,其时域波形及其频谱、功率谱密度对比分别如图20a、b和c,可以看出单道时域波形和谱特征都较为相似,频谱较宽,主要频率带在0~50 Hz左右.通过对比各种频率范围的噪声在随机噪声中所占的比重可以看到风对树木的作用力是造成山地地区高频干扰的主要来源.
随机噪声是否存在混沌性通过其相轨迹中是否存在奇怪吸引子来判断.周期序列的相轨迹图是一个周而复始的曲线,不存在奇怪吸引子;而混沌序列的相轨迹图则是在一定区域内不规则的混乱曲线,存在奇怪吸引子,实际噪声和模拟单道时域波形的相轨迹分别如图21a和b所示,可以看出模拟噪声和实际噪声有相似的相轨迹,并且都不是简单的周期性的往复曲线,存在奇怪吸引子,具有混沌特性.
模拟噪声与实际噪声振动图的频率分布如图22a和b,累积分布对比如图22c.统计量特征对比如表1,可以看出两者趋于一致.通过对模拟噪声和实际噪声振动图的各项性质进行对比,不难发现模拟噪声与实际噪声在时域内基本相似.
3.2 波剖面特征对比
在地震勘探记录中,波剖面是在某一时刻由空间阵列检波器接收到的多道记录,即随机噪声的空域波形,选取任意时刻,文中取t=644 ms时,实际噪声和模拟噪声的波形对比及其波数谱如图23a和b所示.统计特性如图24及表2所示.通过对模拟噪声和实际噪声波剖面的各项性质进行对比,不难发现模拟噪声与实际噪声在空域内基本相似.

表1 模拟噪声与实际噪声振动波形统计性质对比

表2 模拟噪声与实际噪声波剖面统计性质对比
通过比较模拟噪声场和实际噪声场任意位置(振动图)和任意时刻(剖面图)的各项特性,结果显示了模拟噪声与实际噪声基本一致,说明了地震勘探随机噪声模拟方法的可行性.
建立随机噪声的理论模型使得对随机噪声的研究不再局限于对其性质,特征参数的总结,而是能够依据不同测区的环境,通过改变相关参数得到相应的模拟噪声,以山地地区的随机噪声为例,改变风速条件,地表地质参数,树木特征参数等,就能从非山地地区的噪声场得到山地地区噪声场,为下一步研究其传播特性和压制打下基础.首先,随机噪声的性质不是一成不变的,而是随传播介质等因素的变化发生改变,通过随机噪声建模,可以从理论上解释引起噪声性质发生变化的原因.其次,通过对随机噪声进行建模得到不同测区的模拟随机噪声后,在合成地震记录时,不再任意测区的合成记录都使用高斯白噪声作为其背景噪声,而是将该测区的模拟随机噪声当作背景噪声,为后续处理实际数据时方法选择,参数调整减小工作量.再次,能够从理论上分析不同测区随机噪声的组成部分及其特性,从而在大量的噪声压制方法中选择出适当的滤波方法.总之,对随机噪声进行理论建模,对以后的噪声压制和野外数据采集都有一定的理论指导作用.
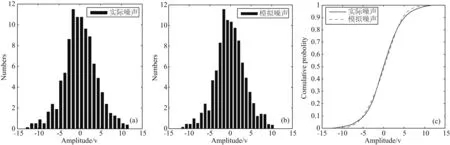
Fig.22 单道振动图频率与累积分布

Fig.23 t=644 ms 时刻波剖面波形对比
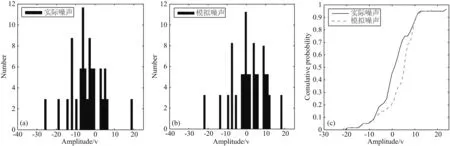
Fig.24 t=644 ms波剖面噪声频率与累积分布
4 结论
本文将随机噪声分为自然噪声和人文噪声两类,根据云南山地地区地震勘探数据的采集环境,自然噪声主要是风吹地表引起的地表发生形变,吹过树木时,树木发生振动以及枝叶摆动发出的声音引起的噪声,人文噪声主要是机器开动,人走动等引起的近场噪声和工厂、交通等引起的远场噪声.分别对不同的噪声源函数进行模拟,以波动方程为传播方程,通过求解非齐次波动方程得到各个噪声源引起的噪声,叠加后得到的综合波场就是时空域的随机噪声.分别将模拟噪声和实际噪声的振动图特征和波剖面特征进行对比,可以看出模拟造声与实际噪声高度相似,证明了文中模拟方法的有效性,为之后对压制随机噪声选择合适的方法打下基础.
附录
本文使用弹性波波动方程和声波波动方程.假设激发波以球面形式向外传播被检波器接收.波动方程描述了波传播的基本规律,通过波动方程解表征随机噪声的波场特征.根据波传播理论,波在理想介质中传播时,满足方程:

(29)

根据弹性动力学理论,弹性波在均匀、各向同性、半无限大的理想介质中传播时,假设震源点位于地表,Z轴垂直向下,方程(29)满足无应力边界条件为
(30)
(31)
式中λ、μ为拉梅常数,ux、uz分别为X方向、Z方向的位移分量且可以表示为
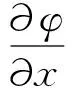
(32)
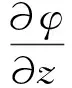
(33)
式中φ、ψ分别为横波和纵波的标量位.
声波在无限大理想介质中传播时满足自由边界条件.得到各个噪声源函数后选择合适的方法(本文选取有限差分法)求解波动方程,得到不同噪声源下的噪声波形,叠加后得到的综合波场即为随机噪声.
Barajas-Olade C, Ramadan A. 2011. Is it possible to conduct seismic wind noise experiments in a wind tunnel?. ∥Presented at the 73rd EAGE Conference and Exhibition Incorporating SPE EUROPEC. Vienna, Austria: European Association of Geoscientists and Engineers, 238.
Bonnefoy-Claudet S, Cotton F, Brad P Y. 2006a. The nature of noise wavefield and its applications for site effects studies: A literature review.Earth-ScienceReviews, 79(3-4): 205-227.
Bonnefoy-Claudet S, Cotton F, Brad P Y. 2006b. H/V ratio: a tool for site effects evaluation. Results from 1-D noise simulations.Geophys.J.Int., 167(2): 827-837.
Bourg D M. 2002. Physics for Game Developers. Beijing: Publishing House of Electronics Industry, 135-137.
Coder K D. 2000. Estimating wind forces on tree crowns. Athens, Georgia: The University of Georgia, http:∥warnell.forestry.uga.edu/service/library/for00-016/for00-016.pdf.
Davenport A G. 1961. The spectrum of horizontal gustiness near ground in high winds.Roy.Meteor.Soc., 87(372): 194-211.
Feng H, Xiao Z Z, Li Z L, et al. 2013. Research on the wind speed spectrum of complex mountainous environment.JournalofHunanUniversity(NaturalSciences) (in Chinese), 40(1): 27-32.
Li X. 2010. Study on characteristics of wind field in ground layer on hilly terrain (in Chinese)[Ph. D. thesis]. Chongqing: Chongqing University.Li Y, Peng J L, Ma H T, et al. 2013. Study of the influence of transition IMF on EMD do-noising and the improved algorithm.ChineseJ.Geophys. (in Chinese), 56(2): 626-634, doi: 10.6038/cjg20130226.
Liu Y P, Li Y, Nie P F, et al. 2013. Spatiotemporal time-frequency peak filtering method for seismic random noise reduction.IEEEGeoscienceandRemoteSensingLetters, 10(4): 756-760.
Lu L Y, He Z Q, Ding Z F, et al. 2014. Investigation of ambient seismic noise sources in the North China array.ChineseJ.Geophys. (in Chinese), 57(3): 822-836, doi: 10.6038/cjg20140312.McNamara D E, Buland R P. 2004. Ambient noise levels in the Continental United States.BulletinoftheSeismologicalSocietyofAmerica, 94(4): 1517-1527.
Ministry of Housing and Urban-Rural Development of the People′s Republic of China (MOHURD). 2012. GB 50009-2012
Load Code for the Design of Building Structures (in Chinese). Beijing: China Building Industry Press.
Pan J T, Wu Q J, Li Y H, et al. 2014. Ambient noise tomography in northeast China.ChineseJ.Geophys. (in Chinese with), 57(3): 812-821, doi: 10.6038/cjg20140311.
Russell D A, Titlow J P, Bemmen Y J. 1999. Acoustic monopoles, dipoles, and quadrupoles: An experiment revisited.Am.J.Phys., 67(8): 660-664.
Shinozaka M, Jan C M. 1972. Digital simulation of random processes and its applications.JournalofSoundandVibration, 25(1): 111-128.
Sorrells G G, McDonald J A, Der Z A, et al. 1971. Earth motion caused by local atmospheric pressure changes.Geophys.J.Roy.Astr.Soc., 26(1-4): 83-98.
Sun Y, Li Z L, Huang H J, et al. 2011. Experimental research on mean and fluctuating wind velocity in hilly terrain wind field.ActaAerodynamicaSinica(in Chinese), 29(5): 593-599.
Taylor P A, Lee R J. 1984. Simple guidelines for estimating wind speed variations due to small scale topographic features.Climatol.Bull,18(2): 3-22.
Tian H Q. 2009. Advances in Industrial Aerodynamics (in Chinese). Changsha: Central South University Press, 20-23.
Tian Y N, Li Y, Yang B J. 2014. Variable-eccentricity hyperbolic-trace TFPF for seismic random noise attenuation.IEEETransactionsonGeoscienceandRemoteSensing, 52(10): 6449-6458.
Wang L. 2006. Building and analysis of dynamic model for windthrow of spruce (in Chinese)[Ph. D. thesis]. Harbin: Harbin Institute of Technology.
Wang Z H. 1994. Simulation of wind loading.JournalofBuildingStructures(in Chinese), 15(1): 44-52.
Ward H S, Crawford R. 1966. Wind-induced vibrations and building modes.Bull.Seismol.Soc.Am., 56(4): 793-813. Williams J E F, Hawkings D L. 1969. Sound generation by turbulence and surfaces in arbitrary motion. Philosophical Transactions of the Royal Society of London.SeriesA,MathematicalandPhysicalSciences, 264(1151): 321-342.
Wu N, Li Y, Yang B J. 2011. Noise attenuation for 2-D seismic data by Radial-Trace time-frequency peak filtering.IEEEGeoscienceandRemoteSensingletter, 8(5): 874-878.
Yan S, Zheng W. 2005. Wind load simulation by superposition of harmonic).JournalofShenyangArch.andCiv.Eng.Univ. (in Chinese), 21(1): 1-4.
Young C J, Chael E P, Withers M M, et al. 1996. A comparison of the high-frequency (>1 Hz) surface and subsurface noise environment at three sites in the United States.Bull.Seismol.Soc.Am., 86(5): 1516-1528.
Zhang Q. 2012. Aeroacoustics Foundation (in Chinese). Beijing: National Defence Industry Press, 96-142.
Zhao P P, Chen J H, Campillo M, et al. 2012. Crustal velocity changes associated with the WenchuanM8.0 earthquake by auto-correlation function analysis of seismic ambient noise.ChineseJ.Geophys. (in Chinese), 55(1): 137-145, doi: 10.6038/j.issn.0001-5733.2012.01.013.
Zhu L B, Wang Q D. 2011. An expression of the cross-correlation of ambient seismic noise: A derivation based on the surface-wave theory.ChineseJ.Geophys. (in Chinese), 54(7): 1835-1841, doi: 10.3969/j.issn.0001-5733.2011.07.017.
附中文参考文献
冯宏,肖正直,李正良等. 2013. 复杂山地环境下脉动风速谱研究. 湖南大学学报(自然科学版), 40(1): 27-32.
李鑫. 2010. 山地地形的近地风场特性研究[硕士论文]. 重庆: 重庆大学.
李月, 彭蛟龙, 马海涛等. 2013. 过渡内蕴模态函数对经验模态分解去噪结果的影响研究及改进算法. 地球物理学报, 56(2): 626-634, doi: 10.6038/cjg20130226.
鲁来玉, 何正勤, 丁志峰等. 2014. 基于背景噪声研究云南地区面波速度非均匀性和方位各向异性. 地球物理学报, 57(3): 822-836, doi: 10.6038/cjg20140312.
潘佳铁, 吴庆举, 李永华等. 2014. 中国东北地区噪声层析成像. 地球物理学报, 57(3): 812-821, doi: 10.6038/cjg20140311.
孙毅, 李正良, 黄汉杰等. 2011. 山地风场平均及脉动风速特性试验研究. 空气动力学学报, 29(5): 593-599.
田红旗. 2009. 工业空气动力学研究进展. 长沙: 中南大学出版社, 20-23.
王琳. 2006. 云杉风倒动力学模型的建立与分析[硕士论文]. 哈尔滨: 哈尔滨工业大学.
王之宏. 1994. 风荷载的模拟研究. 建筑结构学报, 15(1): 44-52.
阎石, 郑伟. 2005. 简谐波叠加法模拟风谱. 沈阳建筑大学学报(自然科学版), 21(1): 1-4.
张强. 2012. 气动声学基础. 北京: 国防工业出版社, 96-142.
赵盼盼, 陈九辉, Campillo M等. 2012. 汶川地震区地壳速度相对变化的环境噪声自相关研究. 地球物理学报, 55(1): 137-145, doi: 10.6038/j.issn.0001-5733.2012.01.013.
中华人民共和国住房和城乡建设部. GB 50009-2012建筑结构荷载规范. 北京: 中国建筑工业出版社.
朱良保, 王清东. 2011. 地震背景噪声互相关函数的面波理论表达形式. 地球物理学报, 54(7): 1835-1841, doi: 10.3969/j.issn.0001-5733.2011.07.017.
(本文编辑 张正峰)
Wave equation modeling of random noise in seismic exploration for metal deposits in mountainous areas
LI Guang-Hui, LI Yue*
DepartmentofInformationandEngineering,JilinUniversity,Changchun130012,China
Random noise attenuation is one of key problems in seismic data processing. The existence of random noise greatly reduces the signal-noise ratio (SNR) of seismic records. Although there are lots of filtering methods available to attain this end, it is inconvenient to select a more appropriate tool for random noise attenuation, of which the characteristics change with the fields of seismic data collection. The understanding of how random noise is generated is the first requirement to solve this problem.We model seismic random noise on land to analyze the characteristics of noise generated by different sources in seismic records. Taking the noise collected in the mountainous region in Southern China for example, the noise sources include natural sources such as wind friction over the ground surface, tree vibrations and rustles caused by wind loads, and cultural sources including running machines, footsteps of people and animals around the geophones and traffic, factories, people′s daily lives in the distance. For convenience of computation, it is assumed that all of the sources contribute as point-sources in their designated areas, the function of each kind of noise source is decided according to the corresponding theory, including wind load theory, effect of mountain on wind speed, transverse vibration of beam, aeroacoustics, pseudoharmonic signal and so forth. The noise propagates by wave equation and random noise record is the superposed wave field. The theoretical model of random noise is built, the factors which influence noise characteristics are analyzed in theory, e.g. wind speed, surface roughness, mountain size etc.When the source functions are finalized, all kinds of noise wave-fields can be obtained by solving wave equations. The synthetic records, the single channel waveforms and their frequency spectrums of each kind of noise are shown. The results show that the noise caused by branches and leaves of trees rustle in wind is the major high-frequency component. Seismic random noise is a temporal and spatial random process. As a superposed wave-field, it is composed of vibrograms and wave profiles when the distance or time is a constant. Therefore, the characteristics of the simulated noise record are compared with the real noise in the time domain (vibrogram) and space domain (wave profile), respectively, which include frequency spectrum (wave number spectrum in the space domain), power spectral density, phase locus(only in time domain), mean, variance, kurtosis, skewness, frequency distribution, and cumulative distribution function in the time domain. The comparison results both of vibrogram and wave profiles show the similarity between the simulated noise and the real one.The comparison results demonstrate the feasibility of the proposed method. When a theoretical model of seismic random noise is built, the simulated noise in different data collection regions can be obtained by adjusting the parameters, and noise propagation characters can be analyzed in theory. The simulated noise in the corresponding regions can be used as the background noise instead of white Gaussian noise. A more suitable filtering method and its parameters can be selected and adjusted by analyzing the main component of noise and its mathematical expression.
Seismic exploration for metal deposits; Random noise; Wave equation; Wave field simulation
深部矿产资源立体探测技术及实验研究(SinoProbe-03)和国家自然科学基金重点项目(41130421)共同资助.
李光辉,女,1986年生,博士研究生,主要从事信号处理研究.E-mail:liguanghui0352@163.com
*通讯作者 李月,女,博士,教授,博士生导师,主要从事信号处理和地震勘探数字处理研究.E-mail:liyue@jlu.edu.cn
10.6038/cjg20151220.
10.6038/cjg20151220
P631
2015-05-16,2015-11-17收修定稿
李光辉, 李月. 2015. 金属矿山地地区地震勘探随机噪声的波动方程模拟.地球物理学报,58(12):4576-4593,
Li G H, Li Yue. 2015. Wave equation modeling of random noise in seismic exploration for metal deposits in mountainous areas.ChineseJ.Geophys. (in Chinese),58(12):4576-4593,doi:10.6038/cjg20151220.

