利用非稳定流求解潜水水文地质参数的降深比值6点法
陈凌颜, 滕 凯
(1.齐齐哈尔市河道管理处,黑龙江 齐齐哈尔 161006; 2.齐齐哈尔市水务局,黑龙江 齐齐哈尔 161006)
利用非稳定流求解潜水水文地质参数的降深比值6点法
陈凌颜1, 滕 凯2
(1.齐齐哈尔市河道管理处,黑龙江 齐齐哈尔 161006; 2.齐齐哈尔市水务局,黑龙江 齐齐哈尔 161006)
利用Boulton井流公式求解潜水非稳定流条件下的水文地质参数,是涉及4个未知数的超越方程,无法通过常规的解析法直接获解.传统的图解法不但受图表束缚,而且求解过程繁复、成果精度存在人为误差.文中采用优化拟合方法,在工程适用参数范围内,用较为简单的函数完成了由图表给出的井函数数值关系的替代,并利用降深比值关系,通过选取水位降深曲线上的6个点,经整理获得了仅含1个未知量的表达式,经简单试算即可完成参数求解,结果更接近工程实际,且计算过程简捷,不依赖图表,便于实际工程应用.
越流补给;水位降深比值;水文地质参数;优化拟合;简化计算
潜水是地下水资源的重要组成部分,具有埋藏深度小、补给条件好、开发利用成本低等优点,在地下水资源的开发利用中占有重要地位.因此,研究地下潜水水文地质参数的获取方法,对定量评价地下潜水水资源量及制订防污染计划意义重大.因利用Boulton井流公式求解潜水非稳定流条件下水文地质参数为涉及4个未知数(即:含水层导水系数T,m2/h;含水层弹性释水系数S;给水度μ;越流因数D,m)的超越方程,无法通过解析法直接完成参数求解.目前,工程上普遍采用图解法[1],即降深-时间量板法[2]、标准曲线比对法和直线图解法[3-4].而现有利用计算机软件实现的智能算法均派生于Theis公式[5-7],并不能直接应用于Boulton井流公式.由于标准曲线比对法需分别完成对抽水初期及后期降深曲线与标准曲线的手动拟合,实际工作不但受图表束缚,而且求解成果因受标准曲线的密度及比对过程中人为因素的影响,其精度难免存在误差[8];直线图解法是在假定抽水后期潜水滞后重力给水对水位降深没有影响的情况下,降深与时间的对数可用直线关系表示,而实际工程并非完全如此,另一方面,由于利用所取直线的斜率确定的切线位置不唯一,所得参数也很难一致,有时甚至差距很大[9].因此,研究提出一种计算方法简单、求解成果精度可靠的潜水非稳定流情况下水文地质参数的获取方法,对进一步提高求解潜水含水层水文地质参数的工作效率和成果精度具有重要意义.
笔者采用优化拟合方法[10-12],通过对潜水非稳定流井函数标准曲线的线型分析,借助现有表格给出的井函数数值对应关系,通过逐次逼近拟合计算,获得了潜水非稳定流井流函数的简化替代公式.并利用该公式通过降深比值关系,经数学推导获得了通过选取抽水降深关系曲线上的6个点直接完成相关水文地质参数求解的计算公式,所得参数结果更接近工程实际,计算方法简单直接,可在实际工程中推广应用.
1 公式的建立
1.1 Boulton模型
根据Boulton理论,在潜水含水层中一完整井以定流量Q进行连续抽水,如图1所示,其含水层的水位变化可用如下公式表示[13]:
(1)
(2)
(3)
(4)
(5)
(6)
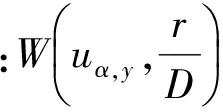
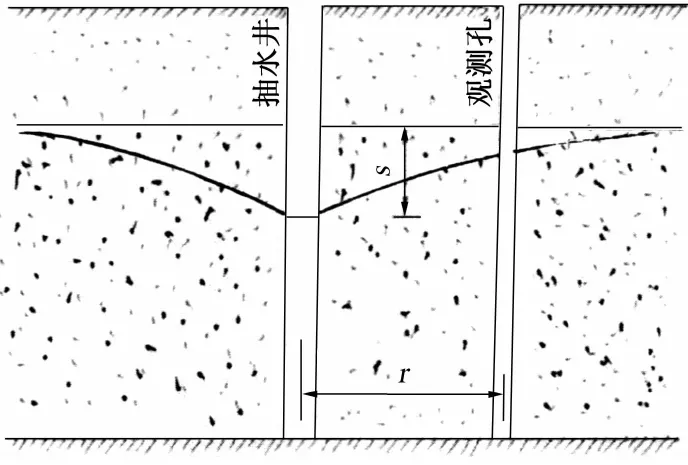
图1 潜水含水层示意图

1.2 降深比值求解法
由于利用潜水非稳定流抽水资料确定水文地质参数需分别根据抽水初期和后期的计算结果才能最终确定,因此,下面分别就抽水初期和后期的参数求解方法进行研究.
1.2.1 抽水初期
在抽水初期(抽水主孔或观测孔)的降深曲线上分别选取(t1,s1)、(t2,s2)和(t3,s3),则由式(1)可得到以下方程组:
(7)
(8)
(9)
(10)
(11)
式中:s12,s23分别为与抽水历时t1,t2和t2,t3相对应的降深比值.


图2 W-uα关系曲线
由图2可见,W-uα具有较好的指数函数关系.依据函数曲线的这一特征,经过对多组具有类似曲线形式的备选函数的拟合比选,并以标准剩余差最小为目标函数[14],即:
(12)


(13)
其中:
(14)
(15)
(16)
式中:A,B,C均为与参数a及t有关的中间变量.
将式(13)—(16)分别代入式(10)、(11)中,经整理即可获得求解参数a的计算公式,即
(17)
其中:
A21=A2-A1,A32=A3-A2,
(18)
B21=B2-B1,B32=B3-B2,
(19)
C21=C2-C1,C32=C3-C2.
(20)
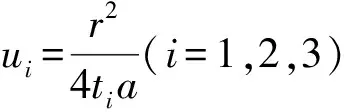

(21)
(22)

(23)
再由式(5)求得弹性释水系数S,即
(24)
1.2.2 抽水后期
采用与利用抽水降深初期资料求解水文地质参数相同的方法,即可完成利用抽水降深后期资料求解水文地质参数的计算.
(25)
其中:
(26)
(27)
(28)
式中:A′,B′,C′均为与参数ay及t有关的中间变量.

(29)
其中:
(30)
(31)
(32)


(33)
(34)

(35)
再由式(6)求得给水度μ,即
(36)
进而可求得潜水含水层的总给水度μ0及给水度特征比值η,即
(37)
2 精度分析


(38)
式中:zi为拟合替代相对误差,%;i为拟合计算中所选取的第i个数据精度比较点.

图3 式(13)替代误差包络线

图4 式(25)替代误差包络线
由图3和图4可见,在工程适用参数范围内,利用本文近似井函数式(13)(或式(25))替代文献[2]附表2中理论值的最大相对正、负误差分别为5.21%和-5.37%,完全可以满足实际工程的设计精度要求.
3 算 例
选文献[2]算例:在某地第四纪含水层中进行抽水试验,含水层厚7.75 m,由含砾石的中砂组成.隔水底板为砂岩.抽水井为完整井,井径为0.32 m,抽水持续时间为48 h 50 min,抽水流量Q=53 m3/h,抽水井至观测孔的距离r=10 m.抽水试验资料见表1,试计算该含水层水文地质参数.
根据表1绘制s-t关系曲线,如图5所示,并对曲线进行认真修正,剔除个别点因测量或设备因素产生的误差影响.
分别在s-t关系曲线的初期段和后期段上选取:t1=0.75 min,s1=0.137 m;t2=2.00 min,s2=0.185 m;t3=10.00 min,s3=0.221 m;t4=670.00 min,s4=0.373 m;t5=1 450.00 min,s5=0.429 m;t6=2 650.00 min,s6=0.475 m.

表1 观测孔实测资料
对抽水初期阶段,依据上述已知参数,并设a=695 100 m2/d,由式(14)—(16)及式(18)—(20)即可分别求得:A1=-1.912 389,A2=-1.951 335,A3=-1.971 105,B1=1.179 148,B2=0.638 819,B3=-0.215 999,C1=0.594 548,C2=1.130 126,C3=1.673 282,A21=-0.038 946,A32=-0.019 771,B21=-0.540 328,B32=-0.854 818,C21=0.535 577,C32=0.543 156,s12=0.740 541,s23=0.837 104.

图5 s-t关系曲线
将上述参数代入式(17)可求得等号左、右两端分别为:


由上述计算结果可得该潜水含水层导水系数T的平均值为


总给水度及给水度特征比值为
μ0=μ+S=0.060 43;
4 结 语
依据抽水降深比值关系,对以图表形式给出的潜水非稳定流井函数值进行函数替代,实现了利用s-t曲线上的6个点完成4个水文参数的求解目标,与现行的其他方法比较,具有以下特点.
1)公式的表达形式比较简单、计算过程简捷直观.由于计算所利用的6个点均取自实际抽水降深曲线,因此,所获结果与其他方法比较,更接近工程实际.
2)本文求解方法不受图表束缚及标准曲线族密度影响,避免了图表取值的人为误差及反复进行拟合曲线比对的舍取之繁,便于实际推广应用.
3)为有效提高计算结果的精度,考虑水位降深观测成果可能存在误差,在利用本文方法计算前,可根据s-t的观测成果完成s-t曲线绘制,并通过s-t曲线修正相关水位降深值s.
4)利用s-t曲线进行(t1,s1)—(t6,s6)的6个点选取时,为使各点具有更好的代表性,应尽量将点(t1,s1)—(t3,s3)的3个点选在s-t曲线斜率较大区段(抽水前期区段),将(t4,s4)—(t6,s6)的3个点选在s-t曲线的后区段(抽水后期时段).
5)采用与本文类似的方法也可完成类似情况下的水文地质参数的简化求解计算问题,本文不详述.
[1]段乃金.解析法求潜水含水层水文地质参数的对比分析[D].西安:长安大学,2010.
[2]供水水文地质手册编写组.供水水文地质手册[M].北京:地质出版社,1990.
[3]陈崇希,林敏.地下水动力学[M].武汉:中国地质大学出版社,1999.
[4]张元禧,施鑫源.地下水水文学[M].北京:水利水电出版社,1998.
[5]高瑞忠,朝伦巴根,贾德彬,等.基于非稳定流抽水试验的BP神经网络确定含水层参数研究[J].沈阳农业大学学报,2004,35(5-6):510-512.
[6]魏连伟,邹景力,张建立,等.模拟退火算法反演水文地质参数算例研究[J].吉林大学学报:地球科学版,2004,34(4):612-614.
[7]郭建青,李彦,王洪胜,等.确定含水层参数的混沌序列优化算法[J].中国农村水利水电,2006(12):26-29.
[8]李伟,赵燕容,朱旭芬,等.自动配线法求水文地质参数的优化路径法研究[J].勘察科学技术,2013(2):6-10.
[9]李炳森.利用抽水试验降深比值求水文地质参数[J].煤炭技术,2005,24(8):74-75.
[10]滕凯.标准门洞形过水断面临界水深的简化计算[J].华北水利水电学院学报,2012,33(5):1-3.
[11]滕凯.马蹄形断面隧洞正常水深的简化计算法[J].华北水利水电学院学报,2013,34(5):31-33,76.
[12]滕凯,张丽伟.弧底梯形渠道收缩水深计算方法的简化[J].华北水利水电学院学报,2013,34(3):55-58.
[13]薛禹群,吴吉春.地下水动力学[M].3版.北京:地质出版社,2010.
[14]王慧文.偏最小二乘回归法及其应用[M].北京:国防工业出版社,1999.
[15]阎凤文.测量数据处理方法[M].北京:原子能出版社,1988.
(责任编辑:乔翠平)
Six Point Method of Drawdown Ratio for Solving Hydrogeological Parameters of Phreatic Water under Unsteady Flow Condition
CHEN Lingyan1, TENG Kai2
(1.Tsitsihar River Management Office, Tsitsihar 161006, China; 2.Tsitsihar Water Authority, Tsitsihar 161006, China)
During solving hydrogeological parameters of phreatic water under unsteady flow Condition by Boulton well-flow formulas, the transcendental equations containing four unknown numbers are involved, which are not directly solved by the conventional analytical method. Not only the traditional descriptive geometry solution is bounded by charts, but also the solution procedure is complicated, and the precision of results is affected by personality errors. In this article, the optimal fitting method was used to finish the replacement of magnitude relation of well function given by charts with simpler functions, the expressions containing one unknown number were obtained through utilizing the relation of drawdown ratio and selecting six points in drawdown curves, the parameter solving was completed through simple and tentative calculation, and the solutions were much more approximate to the practice, the solution procedure was simple, did not rely on charts, and was convenient for practical application.
leakage recharge; drawdown ratio; hydrogeological parameters; optimum fitting; simplified calculation
2014-11-08
齐齐哈尔市科技攻关项目(NYGG201301).
陈凌颜(1982—),女,黑龙江肇源人,工程师,主要从事工程建设管理方面的研究. 滕 凯(1957—),男,黑龙江齐齐哈尔人,高级工程师,主要从事水利防灾减灾及工程优化设计方面的研究.
10.3969/j.issn.1002-5634.2015.01.002
TV211.12
A
1002-5634(2015)01-0006-06

