基于能量诱导型PSO算法与LSSVM模型的钢铁企业高炉煤气消耗量预测

王红君，白 鹏，赵 辉,2，岳有军

（1.天津理工大学 天津市复杂系统控制理论与应用重点实验室，天津 300384；2.天津农学院，天津 300384）

基于能量诱导型PSO算法与LSSVM模型的钢铁企业高炉煤气消耗量预测

王红君1，白 鹏1，赵 辉1,2，岳有军1

（1.天津理工大学 天津市复杂系统控制理论与应用重点实验室，天津 300384；2.天津农学院，天津 300384）

0 引言

高炉煤气是钢铁企业生产过程中重要的二次能源[1]。国外大型钢铁企业的高炉煤气利用率极高，如日本的新日铁，高炉煤气的回收利用率可达100%，基本实现了零放散。但在国内的各大型钢铁企业中，除宝钢外，其他钢铁企业的高炉煤气回收利用效率普遍较低，相当一部分的煤气资源被放散掉，既浪费了能源，又污染了环境。因此，建立一种有效、精确的预测模型，对煤气消耗量进行准确预测，是解决煤气资源合理调度与降低放散的前提[2]。

高炉煤气是炼铁过程中得到的副产品，主要成分为CO2、CO、H2、N2和少量的CH4[3]。每生产1吨铁，就可获得约2000立方米左右的煤气。在经过除尘处理后，即可作为一种清洁的副产能源使用。高炉煤气的主要用户有炼铁厂的高炉热风炉、轧钢厂的加热炉还有发电厂的低压锅炉等。其中，热风炉是高炉煤气的消耗大户，消耗量约占煤气总量的40%～50%[4]。热风炉主要负责向高炉内输送高温的热风，以保证冶炼的正常进行。其工作周期主要由：燃烧、闷炉、送风、换炉四个步骤组成[5]，而只有在燃烧阶段才消耗煤气，这就使得煤气的消耗曲线有明显的周期波动的特征。在换炉或在休风、减风等操作下，高炉煤气的消耗量又会发生明显的随机波动，大大增加了预测的难度。

综合国内外的研究现状，对高炉煤气消耗量预测的研究方法主要有：时间序列模型、人工神经网络模型、多层递阶模型、支持向量机等。其中人工神经网络与支持向量机是当下预测研究的热点，许多学者对此做了大量富有成效的研究。但是，以上两种方法有其固有的缺陷，例如，人工神经网络结构复杂、鲁棒性差[6～8]。而支持向量机的最优参数难以确定[9]，这会直接影响预测模型的精准度。基于上述研究存在的问题，本文提出能量诱导型粒子群算法优化的最小二乘支持向量机模型（Energy Guided Particle Swarm Optimization- Least Square Support Vector Machine，EGPSO-LSSVM）来预测高炉煤气的消耗量。改进后的粒子群算法不仅表现出较好的收敛能力，而且利用该算法优化的最小二乘支持向量机模型具有更加优越的预测精度。

1 最小二乘支持向量机（LSSVM）

最小二乘支持向量机是在支持向量机的基础上发展而来。最主要的不同点就是将支持向量机中的不等式约束改为了等式约束，用最小二乘线性函数作为损失函数，代替了支持向量机原本的二次规划。下面简要介绍其算法[10,11]：

目标函数的约束方程为：

其中：()φ·为可将数据映射到高维空间的非线性函数；ω为权向量；γ为惩罚系数；b为偏置系数；ek为误差变量。

引入下面的拉格朗日函数求解上述优化问题：

其中：kα为拉格朗日乘子。解下面的偏微分方程：

由于径向基函数结构简单，泛化能力强，本文采用如下径向基函数作为核函数：

其中：σ称作核宽度，它与惩罚系数γ共同决定了最小二乘支持向量机的性能。通过上述方程求解α和b，得出LSSVM模型的输出为：

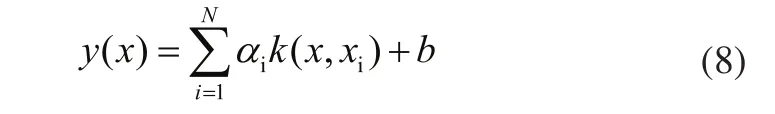
2 粒子群改进算法

粒子群优化算法是一种智能寻优算法，由Kennedy与Eberhart于1995年提出。此算法以模仿鸟群捕食的社会行为为基础，不需要进行复杂的数学计算，只需简单的迭代与信息交换就可以搜索最优值，是一种启发式的寻优方法。其数学描述如下[12,13]：

在D维的搜索空间里有n个粒子，其位置为Xi=(xil,xi2,xi3,…,xiD)；单个粒子飞行时经过的最优位置为：Pi=(pil,pi2,pi3,…,piD)粒子群在飞行中经过的最优位置为：Pg=(pgl,pg2,pg3,…,pgD)。

在迭代中粒子根据以下的公式调整自身状态：

其中：Vi为粒子的飞行速度；Xi为粒子的位置；下标d代表其中的一个维度；t代表迭代的次数；ω为惯性权重，它影响着粒子的飞行速度；c1与c2为学习因子；r1与r2是[0,1]之间的随机数。通过位置与速度的不断迭代更新，粒子群最终可找到空间中的最优解。然而，传统的粒子群算法有全局收敛慢、精度差的缺陷。针对其缺点，本文引进能量剩余函数的概念，模拟生物自身能量循环的过程。给出了粒子速度更新的多选择机制；对于粒子的惯性权重，本文采用一种与种群平均适应度相关联的自适应权重调整方法。确保了粒子群有较好的收敛速度和较高的全局收敛能力。

2.1 粒子群飞行速度的改进

任何生命体的活动都需要先从外界获得能量，然后随着各种生命活动的开展，自身存储的能量又会被逐渐的消耗。就是在这样循环往复的能量流动中，物种才得以发展。离子群算法是一种模仿鸟类飞行的仿生算法，同样也可以将这种生物自身与环境之间能量交换的特点引入到算法中去。粒子的飞行状态是受到自身能量的限制的，而粒子下一刻的飞行状态又会受到外界能量的诱导。

假设粒子i的能量消耗率与粒子的进化代数t相关，自身的初始能量为Fi。经过t代的飞行之后粒子剩余的能量为Ei，可定义如下的能量剩余公式：

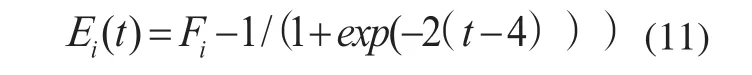
其中：令Fi=1。式(11)称为粒子能量的消化曲线，如图1所示。

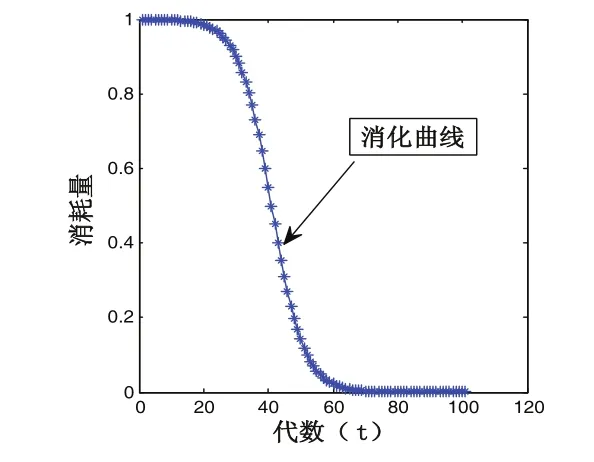
图1 能量消化曲线

上面的曲线可模拟生物体内能量的消耗过程：在初期粒子刚刚获取了较大的能量，且没有与周围环境进行能量的交换，所以能量的下降速率较慢；在中期，粒子与环境能量交换加快，粒子自身能量剩余迅速下降；末期，粒子能量消耗速率放缓，剩余能量趋近于0。

根据上面的能量剩余公式，可定义以下的能量剩余度函数：

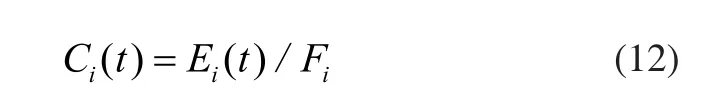
当Ci(t)≥m2，表明粒子剩余能量较多，这时粒子倾向于在自身的最优位置附近搜索。速度的更新公式可表示为：

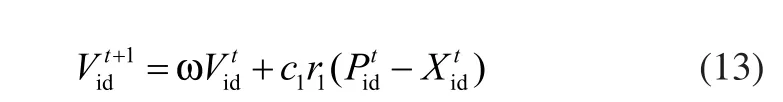
当m1≤Ci(t)＜m2，表明粒子已经进入能量消耗阶段，这时粒子除了在自身的最优位置附近搜索外还会在群体最优位置附近查找。速度的更新公式可表示为：

当m1＜Ci(t)，表明粒子已经进入能量消耗阶段，这时粒子自身的能量基本消耗完毕，需要及时寻找到新的能量源进行补充。粒子不再对自身最优位置进行搜索，而是直接向群体的最优位置靠近。速度的更新公式可表示为：

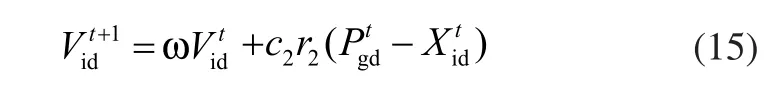
2.2 惯性权重的改进

式(13)～式(15)中的惯性权重ω是粒子群算法中最重要的参数，它决定了粒子的飞行速度。通常，在算法进行的初始阶段，粒子要对一个相对较大的空间进行快速搜索，要求有较大的惯性权重，这样可使粒子获得足够大的飞行速度；而在算法后期，粒子需要在一个较小的空间内精细搜索，所以需要对其赋予较小的权重，以减缓粒子的飞行速度，避免飞过最优值点。通过合理选择惯性权重，可以显著改善算法的收敛速度。

常用的惯性权重调整方法主要是线性调整策略。其中，最主要使用的方法是典型线性递减策略[14]。但这种方法容易造成粒子陷入局部最优。为了克服线性权重调整的缺陷，多位学者相继提出了一系列非线性权重调整措施[15～18]。但这些措施仅仅与当前迭代的次数和迭代的总次数有关，而与种群的平均适应度无直接联系。因此，本文对文献[16]所提出的非线性调整公式进行改进，得到一种通过比较适应度来确定惯性权重的调整策略，具体的调整方式下：

迭代过程中，当个体粒子的适应度大于种群的平均适应度时，即fitness＞avg_fitness。惯性权重表示为：

当个体粒子的适应度小于种群的平均适应度时，即fitness＞avg_fitness。惯性权重表示为；

3 EGPSO-LSSVM预测模型的建立

EGPSO-LSSVM模型的建立步骤如下：

步骤1：选取合适的煤气消耗量样本数据作为训练集与目标集，并对数据进行预处理。

步骤2：初始化粒子群算法的参数。设置粒子群的种群数量、迭代次数、学习因子、惯性权重的上下限及能量剩余度阈值等。

步骤3：初始化粒子的位置与速度及粒子的适应度值。其中，最小二乘支持向量机的核宽度与惩罚因子是改进的粒子群算法要优化的两个参数；适应度函数为期望值与输出值的均方误差。

步骤4：根据2.1节、2.2节的方法计算粒子的能量剩余度并查找初始时单个粒子的适应度与整个种群的平均适应度。

步骤5：进行粒子群的迭代更新。根据粒子的能量剩余度选择合适的速度更新方式，并比较种群的平均适应度与单个粒子的适应度，选择其惯性权重。然后根据式10更新粒子的位置，重新计算粒子的最优适应度值。若优于个体粒子，则用其替换个体粒子的适应度。若优于整个种群，则用其替换整个种群的适应度。

步骤6：满足终止条件或者达到迭代的次数，则退出优化程序，跳转至第7步，否则转至第5步。

步骤7：利用优化后的LSSVM模型对煤气消耗量进行预测。

4 仿真实验分析

4.1 煤气发生量预测的仿真结果

本文以国内某钢铁企业的高炉煤气消耗量数据为实验样本。为保证预测的可靠性，取消耗量中的1000个数据（采样频率为1min），令其中前830个为训练样本，后170个测试样本。利用能量诱导型粒子群算法优化的最小二乘支持向量机进行预测。

粒子群的学习因子c1与c2分别为1.6与1.5；种群规模为15；迭代次数为150次；能量剩余度阈值根据多次实验结果的平均值可取为：m1=0.34，m2=0.69。按照第2节所述方法调整每次迭代时的粒子速度和惯性权重。得到改进的粒子群算法的最佳适应度曲线如图2所示。

图2 改进的粒子群算法适应度曲线

由上图知，EGPSO算法在进化到第21代时，就已经收敛，说明算法具有较好的收敛性。这是由于算法在每一次迭代时都从自身能量的角度进行调整，通过能量剩余度划分粒子最适当的飞行速度，使之能快速的定位最优解位置。其次，非线性惯性权重也使得粒子群在飞行时能按照非线性函数加速，实现全局与局部的搜索。

图3是EGPSO-LSSVM与普通BP神经网络模型的预测效果对比，其中BP神经网络为三层结构，隐含层神经元数量为10个，激发函数选S型正切函数。

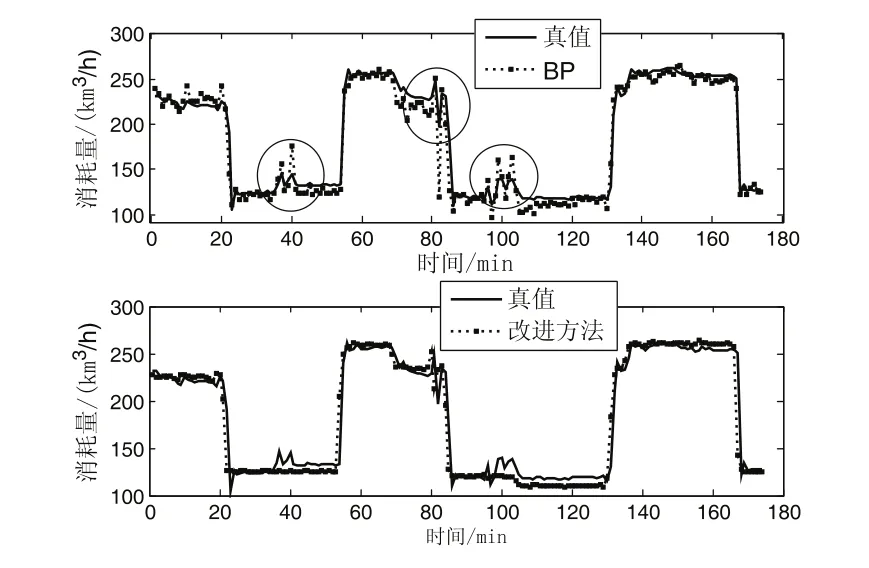
图3 EGPSO-LSSVM与BP神经网络模型的预测效果对比

通过仿真实验可观察出：BP神经网络模型预测的波动性较强，易发生数值抖动（如图3中圆圈所示），这是因为BP神经网络采用经验风险最小化原则，随着预测的进行，模型的预测能力将会变差。而EGPSO-LSSVM模型的预测效果则展示出良好的稳定性，预测得出的波形抖动小，而且更加平滑，预测值也更加贴近真实值。

图4是EGPSO-LSSVM与LSSVM模型的预测效果对比图，以此说明经过优化的模型和未经优化的模型在预测效果上的差异。

图4 EGPSO-LSSVM与LSSVM模型的预测效果对比

由仿真实验观察出：未经优化的LSSVM模型，由于参数的选择无法保证是最优，造成了模型的泛化能力有限，在预测时，会出现较大误差。从图中可知：在37min～59min、72min～86min及103min～129min三个区间段内，LSSVM预测值偏离真实值的程度较大，本文采用的EGPSO-LSSVM模型在整体预测效果上更具优势。

4.2 煤气消耗量预测的误差分析

为定量地说明本文方法的有效性，也为了科学地评价本文建立的EGPSO-LSSVM模型。现采用平均绝对百分比误差(MAPE)、均方误差(MSE)、均方百分比误差(MSPE)三种评价指标，对本文EGPSO-LSSVM模型、BP神经网络模型及LSSVM模型的预测值进行误差比较分析，结果如表1所示。

表1 使用三种评价指标进行误差分析

从表1可知：在给定的三个评价指标上：LSSVM模型的预测效果好于BP神经网络的预测效果，而本文使用的EGPSO-LSSVM模型预测精度又要高于传统最小二乘支持向量机。结果表明本文模型有较高的预测准确性，可以用于高炉煤气消耗量的预测。

5 结束语

本文将能量剩余度函数引入粒子群算法中，通过比较每次迭代更新时粒子的剩余能量度来确定速度，从而确定粒子的搜索方向及飞行速度，有利于快速的寻找到最优解。其次，将惯性权重改进为由平均适应度确定的非线性函数，可实现全局或局部的寻优。

运用改进的粒子群优化的支持向量机模型对钢铁企业高炉煤气的消耗量进行了预测，并与普通BP神经网络、LSSVM模型的预测效果进行了对比，各项误差指标说明：本文建立的优化预测模型具有更高的预测精度，可以为高炉煤气的平衡调度与合理使用提供参考依据。

[1]聂秋平,吴敏,张超,等.一种基于单元分类的钢铁企业煤气调度模型[J].控制工程,2010,17(4):460-465.

[2]李文兵,李华德.钢铁企业高炉煤气系统动态仿真[J].冶金自动化,2009(02):33-37.

[3]丁元明,张学东,张宏勋.高炉煤气成分过程检测[J].炼铁,1997(03):29-32.

[4]张福明.高风温低燃料比高炉冶炼工艺技术的发展前景[J].中国冶金,2013(02).

[5]张大伟.鞍钢煤气调度问题的研究与管理系统开发[D].东北大学热能工程,2011.

[6]张琦,谷延良,提威,等.钢铁企业高炉煤气供需预测模型及应用[J].东北大学学报(自然科学版),2010(12):1737-1740.

[7]肖冬峰,杨春节,宋执环.基于改进BP网络的高炉煤气发生量预测模型[J].浙江大学学报(工学版),2012(11):2103-2108.

[8]刘颖,时飞飞,赵珺,等.基于改进回声状态网络的高炉煤气产耗预测[J].系统仿真学报,2011,23(10):2184-2189.

[9]张晓平,赵珺,王伟,等.基于最小二乘支持向量机的焦炉煤气柜位预测模型及应用[J].控制与决策,2010(8):1178-1183.

[10]Suykens J A K,De Brabanter J, Lukas L, et al. Weighted least squares support vector machines: robustness and sparse approximation[J].Neurocomputing,2002,48(1):85-105.

[11]童晓,孙卫红,李强.一种改进PSO-LSSVM算法在锅炉燃烧优化中的应用[J].制造业自动化,2015(02):12-15.

[12]Kennedy J,Eberhart R. Particle swarm optimization: Proceedings of IEEE International Conference on Neural Networks,1995Nov/Dec 1995.

[13]曹晋宏,李国勇.基于PSO-NP算法的广义预测PID控制及应用[J].制造业自动化,2014(12):34-37.

[14]Yuhui S,Eberhart R C.Empirical study of particle swarm optimization: Evolutionary Computation,1999.CEC 99.Proceedings of the 1999 Congress on,Washington,DC,1999[C].1999.

[15]孙湘,周大为,张希望.惯性权重粒子群算法模型收敛性分析及参数选择[J].计算机工程与设计,2010(18):4068-4071.

[16]王贺,胡志坚,张翌晖,等.基于IPSO-LSSVM的风电功率短期预测研究[J].电力系统保护与控制,2012(24):107-112.

[17]李会荣,高岳林.粒子群优化的速度方程改进与自适应变异策略[J].计算机工程与应用,2010,46(13):47-50.

[18]崔红梅,朱庆保.微粒群算法的参数选择及收敛性分析[J].计算机工程与应用,2007,43(23):89-91.

Consumption forecasting of blast furnace gas in Iron and steel industry based on energy guided particle swarm optimization and least square support vector machine model

WANG Hong-jun1, BAI Peng1, ZHAO Hui1,2, YUE You-jun1

针对钢铁企业高炉煤气消耗量存在的波动大、随机性强、难以预测等特点，引入能量剩余函数，提出了一种与粒子自身能量相关的能量诱导型粒子群（Energy Guided Particle Swarm Optimization，EGPSO）算法。利用其对最小二乘支持向量机（Least Square Support Vector Machine，LSSVM）的参数进行优化，最后采用优化后的最小二乘支持向量机模型（EGPSO-LSSVM）进行高炉煤气消耗量预测。仿真实验表明：改进后的预测模型在平均绝对百分比误差、均方误差、均方百分比误差三项指标上均优于普通BP神经网络模型和普通最小二乘支持向量机模型，可以为高炉煤气资源的合理使用提供依据。

高炉煤气预测；粒子群算法；最小二乘支持向量机；参数优化；惯性权重

王红君（1963 -），女，天津人，教授，硕士，研究方向为流程工业先进控制技术、微机控制和智能控制。

TP391.9

A

1009-0134(2015)07(下)-0067-05

10.3969/j.issn.1009-0134.2015.07(下).21

2015-03-13

天津市科技支撑计划项目（13ZCZDGX03800）