关于我国商业银行贷款竞争的博弈分析

■ 尹锦霞，高凌云，王 兵

一、引言

自中国加入WTO以来，我国商业银行处于与国内外大银行竞争的夹缝中，商业银行在进行贷款决策时经常由于从众心理而模仿他人做出决策，缺乏明确和长远的战略计划，导致不能把握正确的金融市场信息，使得自身陷于生存空间受到多方挤压的社会形势。

国内外学者对商业银行在新时期的发展和竞争关系进行了大量的研究和探索，运用了不同的方法对商业银行贷款业务发展、贷款决策等问题进行分析，内容丰富且研究的侧重点不同，为商业银行的发展提供了启示和建议。方兰认为博弈论作为重要的经济理论和方法，对我国商业银行的经营决策活动以及社会经济发展分析具有重要意义。刘张君运用合作博弈理论分析了商业银行协会内部治理机制，姚洪兴等建立了双寡头有限理性广告竞争博弈模型，并指出当参与人对市场的反应速度变化时,将会出现倍周期分叉和混沌现象。Bischi和Agiza等人分别给出了基于有限理性预期的具有线性成本的双寡头博弈模型和具有非线性成本的双寡头博弈模型，并建立了逆需求函数改变时的双寡头博弈模型。

综合全文，主要讨论以下两方面内容：一、在有限理性和不完全信息的条件下，建立商业银行贷款竞争的博弈模型，分析模型中纳什均衡点及其稳定区域。二、为确切模拟商业银行贷款竞争的状态和金融市场的特点，引入变动成本和风险系数等参数。对在数值模拟过程中出现的周期倍化分叉和混沌现象进行深入分析，并给出合理的经济学解释。

二、模型的建立

（一）模型满足的假设

1.博弈论应当基于这样一个假设上：博弈双方都是基于有限理性而进行贷款决策的。

2.假设模型为双寡头离散动力学模型，两家商业银行分别为博弈方1和博弈方2。每家银行在进行贷款决策时，都处于不完备信息状态。

（二）相关变量的定义

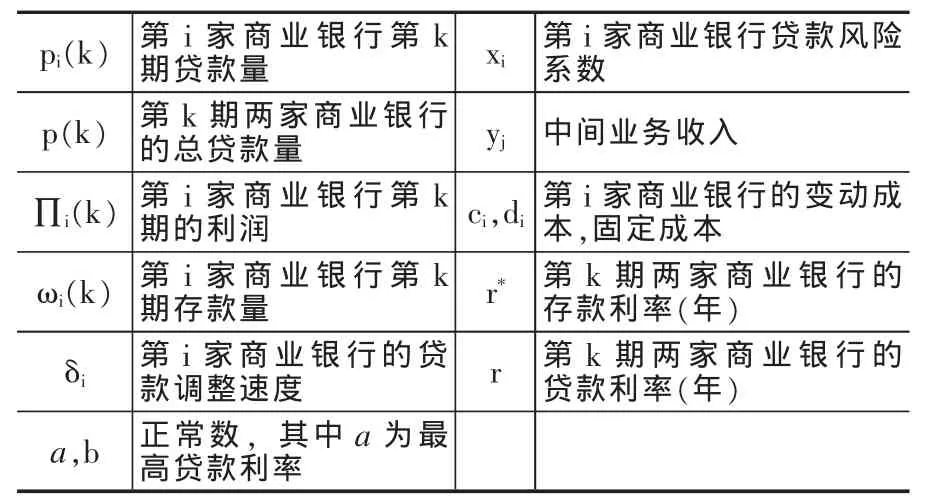
表1 变量的字母表示形式

根据以上变量，结合博弈的过程，我们知道：

1.第k期贷款量总额为：

2.第k期贷款的利率由该期的贷款总量决定，即：

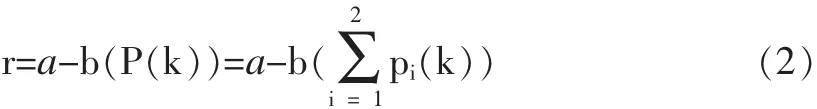
3.银行的利润与银行的存贷款总量分别为ωi（k）和 pi（k）、中间业务收入 yi、变动成本 ci、固定成本di以及风险系数xi有关，综合以上影响因素，得出第i家银行的利润函数∏i的表达形式：

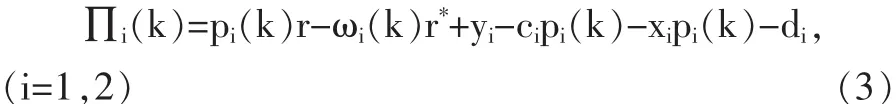
上式整理可得：

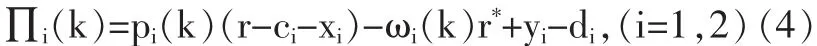
4.联立（1）（4）式，并对（4）式求取关于 pi的一阶偏导数，得出第i家银行的边际利润，表达式如下：

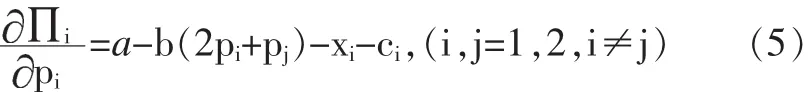
即得以下方程组：

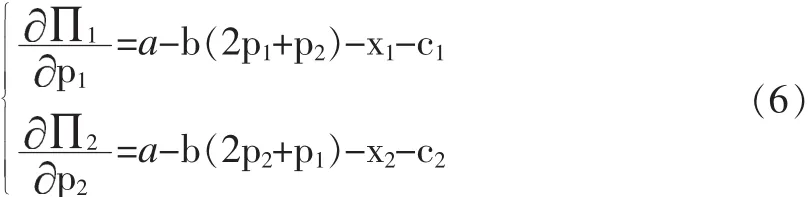
5.现实中商业银行并不具有完全的市场信息，因此不能完全预测未来的贷款变化的情况下，他们主要是基于部分信息而做出未来的贷款决策的。

当（6）式的值，即利润函数的偏导数越大时，利润函数的自变量（贷款量）每增加一单位所引起的利润的单位增量就越大。也就是说，商业银行在某一时期边际利润相对较大时，单位资金的贷款量将为银行带来更大的收益。在这种情况下，银行会在下一时期提高贷款量。同理，当边际利润为负值，则银行就会相应减少在下一期的贷款量以减少损失。因此商业银行每相邻两期的贷款金额满足以下关系：

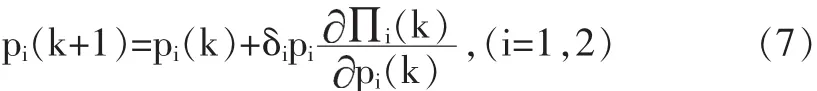
由（7）式得商业银行的利润竞争模型为：

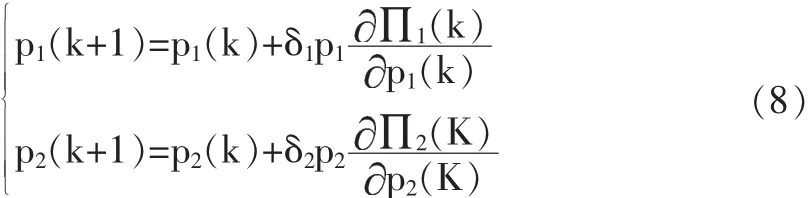
联立（6）、（8）两式，可得：

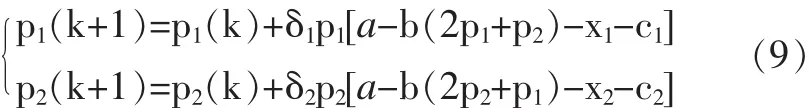
方程组（9）反映了相邻两期的贷款量关系，并以第k期的贷款量表示第k+1期的贷款量。对系统（9）进行动态博弈分析，寻找能使系统处于纳什均衡的不动点，并分析系统在纳什均衡点处的稳定性与各参数的关系，结合经济学的知识，得出各均衡点所对应的商业银行竞争状态。

三、模型的分析

为达到纳什均衡，我们假设系统（9）满足以下条件：

联立（9）、（10）计算可得系统有四个不动点，分别为：

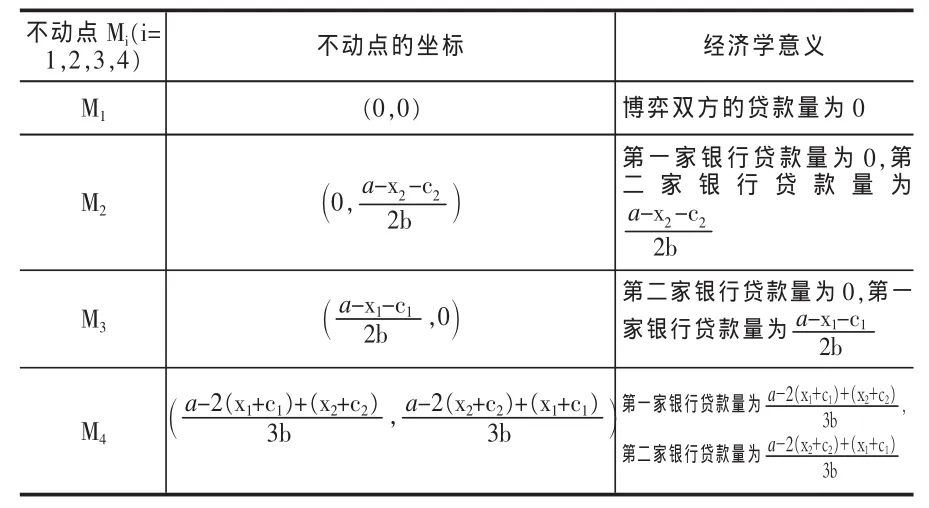
表2 系统（9）的不动点

以上是该模型不动点，下面将对这四个不动点的稳定性进行详细的分析。上表中不动点M1、M2、M3均为有界均衡点，而M4为纳什均衡点。因为商业银行的贷款量不可能为负值，也就是说，a-xi-ci≥0，（i=1，2）且 a-2（xi+ci）+（xj+cj）≥0，（i，j=1，2；i≠j），因此不动点满足以上结论。

定理1：有界均衡点M1是不稳定的。

证明：运用Jacobi矩阵①Jacobi矩阵：雅可比矩阵是一阶偏导数以一定方式排列成的矩阵，其行列式称为雅可比行列式。及其特征值的知识对不动点的稳定性进行如下的分析，在不动点M1=（0，0）处的Jacobi矩阵为：

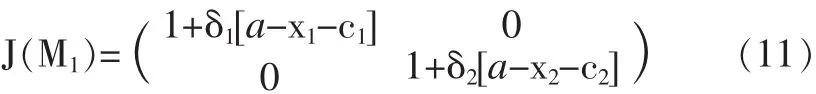
令矩阵 J（M1）的特征值为 λ1（M1）、λ2（M1），由│λE-J（M1）│=0(其中 E 为单位矩阵)得矩阵的两个特征值为 λ1（M1）=1+δ1[a-x1-c1]，λ2（M1）=1+δ2[a-x2-c2]。

我们知道 a-xi-ci≥0，（i=1，2）， 因此 λ1（M1）、λ2（M1）≥1，δ＞0，对于该 Jacobi矩阵，特征值均大于 1，因此可得出结论：不动点M1是不稳定的。在经济学的角度看来，商业银行的经营目的是为了获取更大的利润，如果商业银行的贷款量为零，则商业银行可能处于亏损状态，对于任何一个经营者而言这都是不愿接受的结果。因此商业银行双方均会提高贷款量以获取正利润，商业银行的这种行为将导致贷款量均为零这一均衡情况不稳定。得证有界均衡点M1是不稳定的。

定理2：有界均衡点M2、M3是不稳定鞍点。

根据经济学理论，不动点M2表示当第一家银行但是这种情况是不可能存在的。近些年来我国商业银行的中间业务收入所占比例还处于较低情况，商业银行的盈利主要来源于贷款收入，当其中一家银行的贷款量为0时，另一家银行的贷款量则为身贷款量而打破均衡状态以获取更大利润，同时另一家商业银行也会采取相应的措施以阻止对方对贷款市场的占领。

也就是说，不动点M2是不稳定的鞍点。同理，不动点M3也是不稳定的鞍点。该点表示的是商业银行间不可能稳定存在的一种竞争状态。得证有界均衡点M2，M3是不稳定鞍点。

定理3：若纳什均衡点M4满足朱里准则，则该点是稳定点。

令矩阵 J（M4）的特征值为 λ1（M4）、λ2（M4），由│λE-J（M4）│=0(其中 E 为单位矩阵)得矩阵的两个特征值满足以下方程：

上式中tr J矩阵的J的迹，det J为矩阵J所对应的行列式的值。于是有：

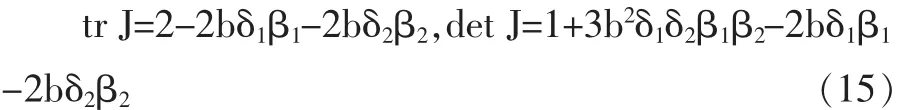
（14）式是关于λ的二次函数，Jacobi矩阵有两个互异实特征值的条件是

联立（15）、（16）式得：

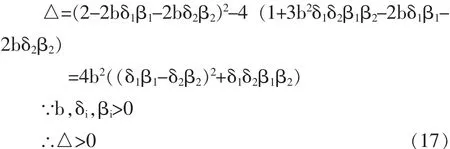
由（14）式可得：该方程的各项系数分别为：a2=1，a1=tr J，a0=det J。 若满足朱里（Jury）准则，则有以下三式：

以上三式中，显然（18）满足，要使纳什均衡点M4是稳定的，（19）（20）式也必须满足，故联立两式得：

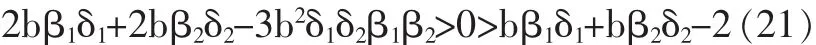
（21）式所表示的数值局域为纳什均衡点M4的稳定区域。我们需要研究银行贷款调整速度对均衡点稳定性的影响，即研究满足上式的δ的取值范围。令第一、二家商业银行的贷款调整速度组成的坐标为（δ1，δ2），由（21）以及 δ1，δ2为正数，可得不等式组：

以上四条不等式分别表示双曲线图上半瓣的下部与下半瓣的上部的交集、直线图下部、横坐标的上部、纵坐标的右部，而不等式组（22）表示这四部分的交集。为了研究稳定区域大小，需找出双曲线、直线、坐标轴的交点，有以下方程：

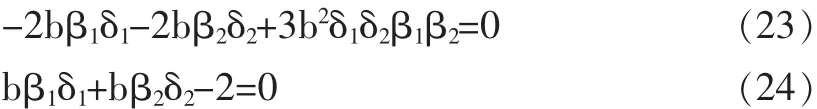
由方程(23)可得，双曲线与坐标轴交点为

Q1=（0，0）

同时可知双曲线与坐标轴交点位于双曲线的下瓣，即双曲线下瓣经过原点，则上瓣位于第一象限。由方程(24)可得，直线与坐标轴交点为

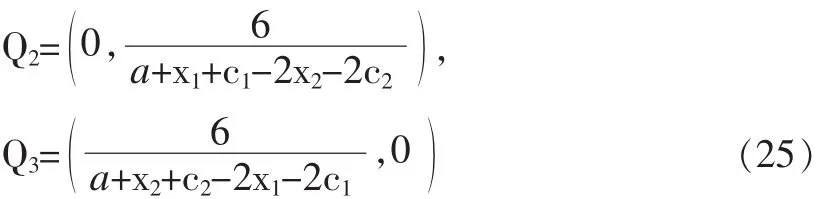
可知，直线与坐标轴交点位于坐标轴正半轴，即直线经过第一象限。至此可知，不等式组(22)的解必定存在，即稳定区域必非空。联立方程(23)(24)可得，直线与双曲线交点满足以下方程：

方程组 (26) 第一式中，△=（-6bβ1）2-4·3b2β12·4=-12b2β12＜0，直线与双曲线无交点，即双曲线上瓣位于直线上方。因而，稳定区域为坐标轴与方程(24)表示的直线所围成的区域，区域大小仅与边界坐标Q2，Q3有关；Q2纵坐标越大，Q3横坐标越大，稳定区域越大。

以上证明可知，纳什均衡点M4在满足朱里准则的条件下是稳定的，即商业银行的贷款调整速度不超出方程组(22)所确定的稳定区域，在多次博弈后，博弈双方最终才能达到区域平衡点。而系统的稳定性依赖于系统参数，将在第四部分对参数进行数值分析和模拟。原命题得证。

实际上，商业银行的贷款量调整速度在反复博弈达到纳什均衡时，银行将获得最大利润，将该不动点M4代入(4)式求得的两家银行的利润分别是：

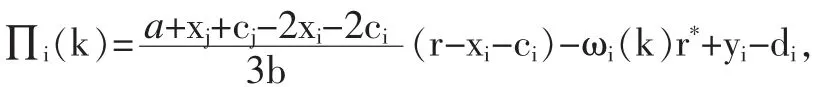
从以上分析可知，贷款量调整速度δi的取值并不改变纳什均衡点，而风险系数xi和变动成本ci则会直接影响到纳什均衡点的贷款量。从Q2，Q3的计算公式(25)可知，当 xi，ci比较小时，稳定区域也比较小；实际上表明，风险系数和变动成本都比较低时，银行会加大贷款量，而贷款量的加大将对稳定性产生较大影响；国家应该利用宏观调控，适当限制银行的贷款量，以维持市场的稳定。我们将在下文进行数值模拟以验证以上观点。

四、数值模拟

为了更好地了解系统参数对系统稳定性的影响，通过以下六组数据对系统进行动态演化过程，通过数值模拟，研究相关参数的变化对系统稳定性的影响。其中，参数xi，ci分别取以下六组数据，参数a均取值为1。

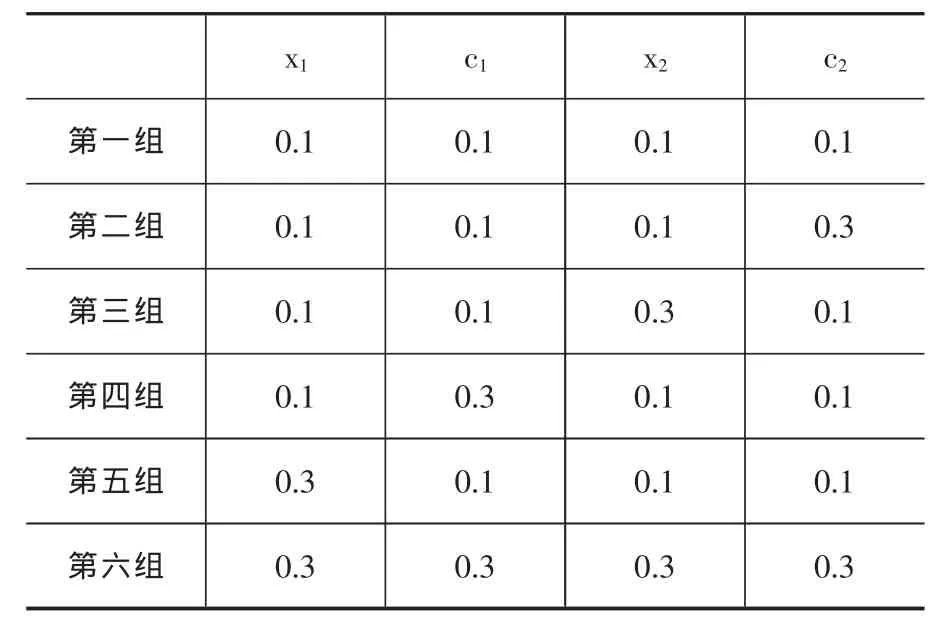
表3 参数的六组模拟数据

将以上数据代入公式(25)，可作出稳定区域，如下的阴影区域：

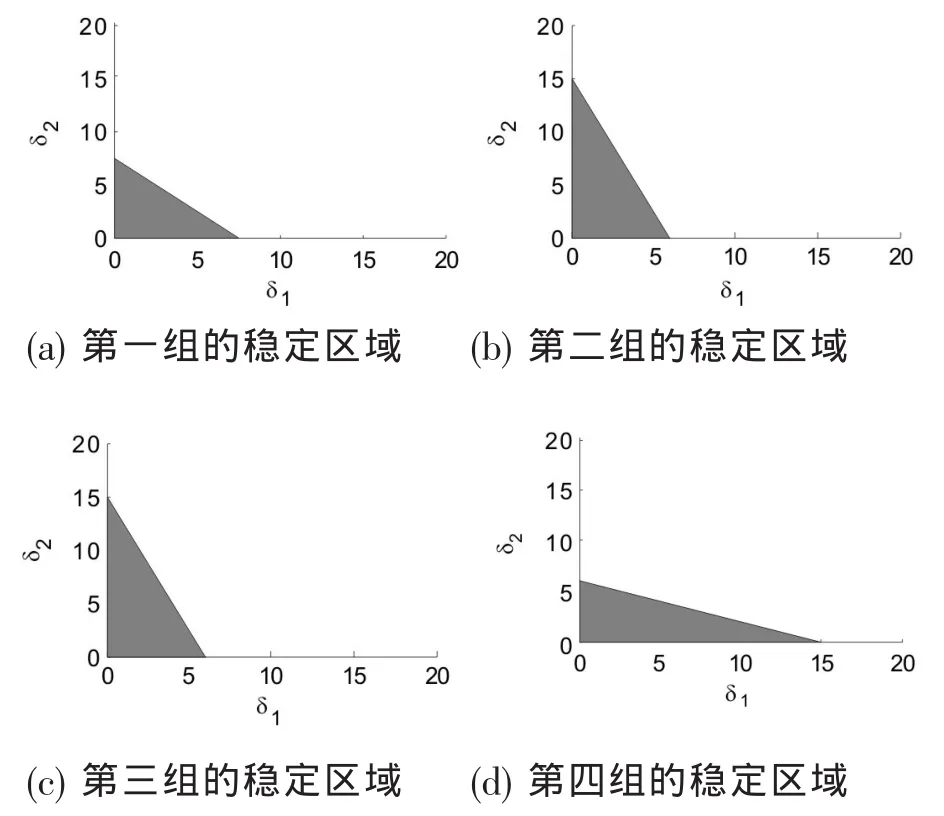
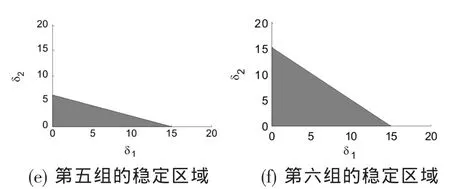
图1 六组数据的稳定区域（阴影部分）

图1 表明参数xi，ci取表3中的指定数值时，δ1，δ2取阴影部分点值时纳什均衡点稳定，否则不稳定。从图 1（a）（f）可发现，以（a）为参照系，参数 xi，ci同时增大时，稳定区域扩大，再分析图 1（a）（b）（c）或（a）（d）（e），同样以（a）为参照系，参数 xi，ci其中一个保持不变，另一个参数增大时，也得出稳定区域扩大。从以上动态演化过程可知，风险系数和变动成本都比较低时，这说明商业银行的管理水平和业务水平比较高，此时银行将加大贷款力度以获取更大的利润，而贷款量过度增加的这种行为将导致金融市场的动荡，稳定区域将减小。因此从图1分析可得出结论，贷款量的调整速度δ1，δ2应适当控制，在国家的宏观调控下，银行适当控制贷款量调整速度和贷款量将有利于系统的稳定性增加，以降低金融市场风险。

为了进一步研究系统的演化过程，取一定数值的参数进行演化模拟，参数取值为下表4：

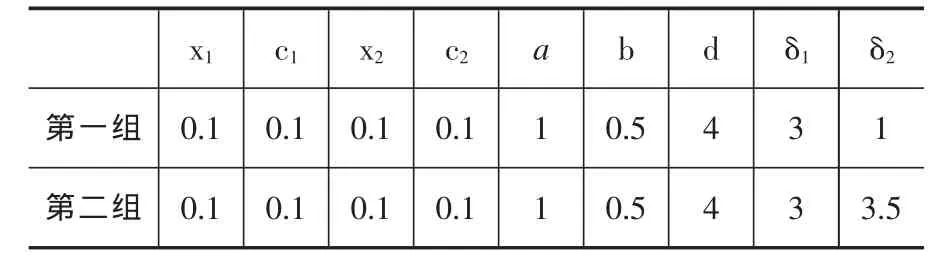
表4 演化模拟参数值

通过计算可以得到，两组参数的不动点均为M4=（0.53，0.53），第一组参数满足不等式(21)，不动点稳定，而第二组参数不满足不等式(21)，则不动点不稳定。 取贷款量初始值 p1（0）=0.48，p2（0）=0.59，代入方程组(9)进行迭代计算，得到如下图2的演化过程：

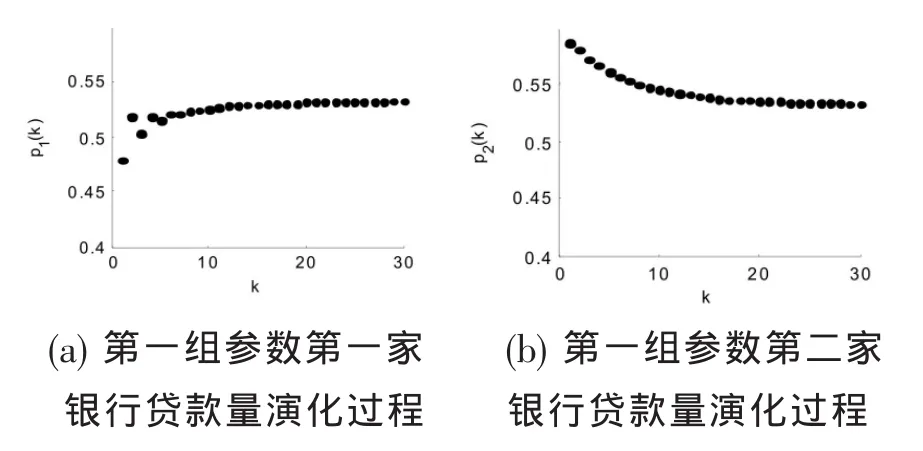
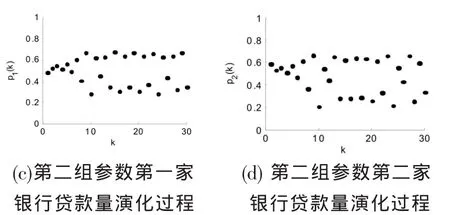
图2 贷款量演化过程

从以上图2(a)和(b)可看出，随着时间的推移，贷款量渐趋于稳定，验证了第一组参数下M4=（0.53，0.53）为稳定的不动点；从图 2(c)和(d)可看出，贷款量在pi（k）=0.53上下有加大幅度的波动，验证了第二组参数下不动点M4=（0.53，0.53）不稳定。

为再进一步研究参数变化对稳定性的影响，可计算出k≥50时，pi（k）的取值情况，其中参数为表4中的值，而δ2从0到4均匀取100个值分别进行计算，得到如下图3所示：

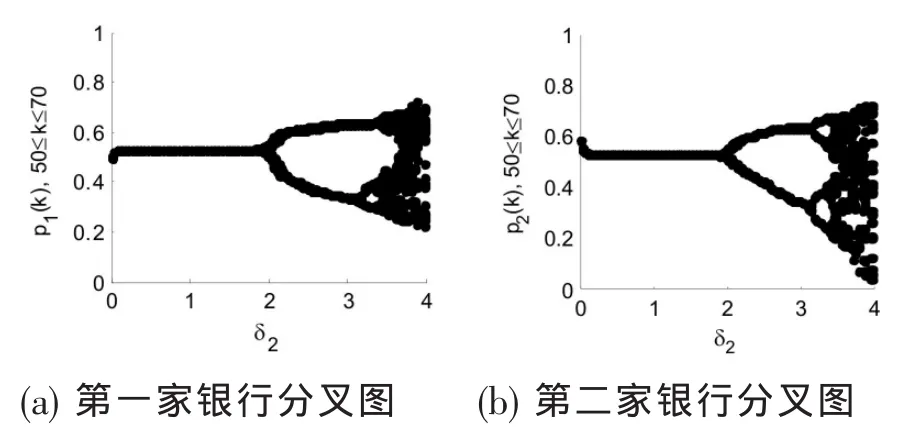
图3 贷款量分叉图

以上图3表明，贷款期数50≤k≤70时，贷款量pi（k）会随着δ2的增加，经过倍周期分叉通向混沌。混沌现象是两家银行都不希望发生的，这会导致银行难以做出长期的计划，银行的贷款调整速度跟不上市场的变化，无法获得稳定的利润，甚至导致整个金融市场的不稳定。因而，应当通过国家宏观调控等方式对银行的贷款量调整速度加以限制，维持我国经济的健康稳定发展。

五、结论

现实社会中，商业银行在进行决策时并不能获取完备信息，因此银行的贷款决策是有限理性的，并且在进行贷款决策的同时要考虑变动成本和风险系数等系统参数。在分析过程中得出商业银行通过调整风险系数等参数以使贷款量控制在一定范围内，有利于商业银行做出合理的贷款决策。数值模拟和演化分析表明当银行的贷款量调整速度满足一定条件时，在有限次博弈后系统可达到纳什均衡的稳定状态，即商业银行的贷款量趋于稳定。否则，商业银行会争相调整贷款量导致贷款量调整速度迅速改变，破坏系统的稳定性。商业银行在无休止的动态博弈下可能出现周期倍化分叉和混沌现象。在这种情况下，银行业的长期规划会受到较大的影响，其利润率难以得到保证。再加上过大的市场波动性及不稳定性，银行的贷款存量调整速度难以赶上市场波动，因此不利于商业银行的长期发展。模型对系统中出现的各种情况给出了经济学解释，可为商业银行贷款决策提供参考。

[1]方兰.博弈论模型在商业银行同质竞争中的应用[J].中国房地产金融，2005，(05):14～17.

[2]刘张君.基于合作博弈的银行业协会治理机制研究[J].金融研究，2007，(12):231～236.

[3]姚洪兴,孟伟业.一类三阶双滞量时滞微分方程的全局渐近稳定性[J].应用数学，2008，（03）:576～580.

[4]Agiza H N,Hegazi A S,Elaadany A A.Complex Dynamics andSynchronization of a Duopoly Game with Bounded Rat ionality[J].Mathemat ics and Comput er in Simulation,2002,58:133～146.

[5]Agiza H N,Hegazi A S,Elaad A A.The Dynamicsof Bowley.sModelw ith Bounded Rationality[J].Chaos,Solitons and Fractals,2001,12:1705～1717.

[6]Bischi G I,Naimzada A.Global Analysis of a Dynamic DuopolyGame with Bounded Rat ionalit y[A].Dynamics Games and Appl ication,1999,20(5).