紫色土典型三角形均质剖面入渗模拟研究
程冬兵,郑艳霞,钱 峰,孙 蓓
(1.长江科学院 水土保持研究所,武汉 430010;2.长江勘测规划设计研究院 生态产业工程有限公司,武汉 430010)
紫色土典型三角形均质剖面入渗模拟研究
程冬兵1,郑艳霞2,钱 峰1,孙 蓓1
(1.长江科学院 水土保持研究所,武汉 430010;2.长江勘测规划设计研究院 生态产业工程有限公司,武汉 430010)
通过室内特制的土壤水分入渗试验装置,分别设置正、倒直角三角形单一质地土壤剖面,探讨紫色土的不规则剖面均质土壤入渗特性。参考Green-Ampt模式思路,建立了紫色土典型三角形均质剖面入渗模型。试验结果显示:粗质地的湿润锋随时间推进速度快于细质地;同一质地,正直角三角形剖面铅直面湿润锋随时间推进速度快于倒直角三角形剖面,但入渗速率小于倒直角三角形剖面;入渗前期,正三角形剖面的斜面湿润锋随时间推进速度快于倒直角三角形剖面,随入渗继续,反而逐渐慢于倒直角三角形剖面。各剖面入渗的湿润锋、入渗速率与时间均呈极显著幂函数关系。建立的紫色土典型三角形均质剖面入渗模型经实测值验证,模拟值与实测值具有非常好的一致性,且可与经验模型相互转换,模型参数也具有一定的物理意义。
紫色土;三角形剖面;水分入渗;均质土;入渗模型
1 研究背景
土壤水分入渗是指水分进入土壤形成土壤水的过程,是降水、地表水、土壤水和地下水相互转化过程中的一个重要环节。土壤水分入渗特性是影响土壤水分运动和水土流失过程的重要因数[1]。由于气象、水文、地质、生物以及人类活动的作用,土壤大都呈现非均一剖面,或质地差异,或结构差异,对土壤的入渗特性均有重要影响[2-3]。如在地形地凹处、坡脚处,或因其它硬坎的拦挡作用,上方流失土壤不断在此外沿原坡面沉积,形成不规则剖面层状土壤。当原坡面为岩石或透水性极低的母质等不透水面时,即为不规则剖面均质土壤。许多学者[3-8]通过不同模式和方法对规则均质土及层状土的入渗机制和模拟技术进行了专门的研究,并取得了巨大进展。然而,目前对于不规则剖面土壤入渗特性的研究非常有限。
本研究通过室内特制的土壤水分入渗试验装置,分别设置正、倒直角三角形均质土壤剖面,探讨紫色土不规则剖面均质土壤入渗特性,建立紫色土典型三角形均质剖面入渗模型,以期为研究紫色土不规则剖面层状土壤入渗特性提供基础。
2 模型建立
由于非均一剖面土壤入渗特性较为复杂,很难利用达西定理或Richards方程进行计算,而Green-Ampt入渗模式成为人们揭示非均一剖面土壤入渗机制和模拟计算的有力工具,并得到了广泛应用。本研究参考Green-Ampt模式思路[9],提出紫色土典型三角形均质剖面入渗模型。
基本假定:在积水入渗过程中,任意时刻的土壤湿润锋剖面概化为2部分(如图1所示),即饱和区和过渡区,饱和区入渗可视为一个活塞流过程,过渡区概化为均一吸力值。

图1 均质土壤三角形剖面入渗示意图Fig.1 Infiltration in triangular profiles of homogeneous soil
2.1 正直角三角形剖面入渗模型
设积水深度为H,土层深度为ZT,铅直面湿润锋的位置为Z,饱和区铅直面湿润锋的位置为Z0,斜面湿润锋的位置为L,坡度为θ,过渡区土壤水吸力为Sf。根据Green-Ampt模型,由达西定律可得表土入渗速率q的表达式为
(1)
式中:Ks为饱和导水率;Z0=L×sinθ;A为过水截面面积。当地表积水深度H很小或入渗时间t较长时,式(1)可转化为
(2)
2.2 倒直角三角形剖面入渗模型
如图1所示,同理可得表土入渗速率q的表达式为
(3)
当地表积水深度H很小或入渗时间t较长时,式(3)可转化为
(4)
3 试验设计与供试土样
3.1 试验设计
土壤水分入渗模拟系统包括试验土箱与供水装置2部分,如图2所示。试验土箱采用有机玻璃按高40 cm(其中填土至35 cm)、宽25 cm、厚6 cm的方形尺寸制成。供水装置采用马氏瓶,可实现在恒定水头下自动供水。
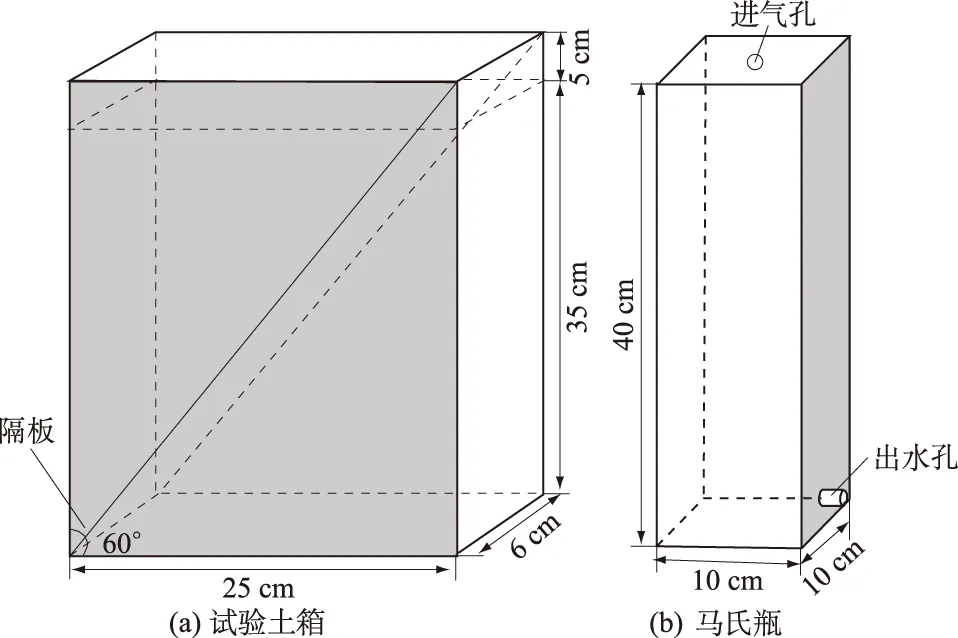
图2 土壤水分入渗模拟试验装置Fig.2 Schematic of the simulation device for soil infiltration
土样经风干过2 mm筛,借助隔板分别设置正直角三角形和倒直角三角形均质土壤剖面,按设计重度分层均匀装入试验土箱。在试验过程中,保持1 cm恒定水位,秒表计时,根据由密到疏的原则,记录入渗时间、湿润锋面和马氏瓶水位。当湿润锋面接近土箱底部时,结束实验。
3.2 供试土样
供试土样为侏罗纪上统逢莱镇组紫色砂页岩发育的中性或石灰性紫色土,取自三峡库区秭归县王家桥小流域。选取2种不种质地紫色土,土样1为壤黏土,土样2为砂黏壤,其基本理化性质如表1。

表1 供试土样理化性质Table 1 Physical and chemical properties of test soils
4 结果与分析
4.1 铅直面湿润锋与时间的关系
水分进入土体,在土体内运动分布的速度与土壤水分所受驱动力及阻力有关,即与水力梯度相关。土壤水分入渗不仅受土壤基质吸力的作用,还受重力的作用,而且随着入渗时间延长,重力作用所占比例逐渐增加,直到成为水分运动的主要驱动力。就是说,随入渗时间延长,水力梯度趋于1,入渗趋于稳定。如图3所示,入渗初期,由于基质吸力为水分运动主要驱动力,水力梯度大,导致单位时间铅直面湿润锋推进较快,表现为铅直面湿润锋随时间变化曲线较陡;到入渗稳定时,由于重力作用逐渐成为主要驱动力,水力梯度趋于1,致使单位时间铅直面湿润锋推进速度也趋于稳定,表现为铅直面湿润锋随时间变化较平缓。

图3 均质三角形剖面铅直面湿润锋与时间关系曲线Fig.3 Curves of vertical wetting front vs.time in triangular profiles of homogeneous soil
土壤水分入渗除与水力梯度相关,还与土壤本身性质相关,如质地、隙度等。不同质地土壤,由于基质作用不同,湿润锋随时间变化过程不同,即湿润锋推进速度不同。另外土壤质地越粗,意味着土壤颗粒间孔隙也越大,大孔隙越有助于水分运动,导致湿润锋推进速度越快。由图3可知,相同剖面入渗设置条件下,土样2的铅直面湿润锋随时间推进速度快于土样1,因为土样2砂黏壤质地较粗,孔隙较大,导水性较好,而土样1壤黏土质地较黏,导水性较差。
同一质地紫色土,正三角形剖面铅直面湿润锋随时间推进速度快于倒直角三角形剖面。

表2 均质三角形剖面铅直面湿润锋与时间关系模型拟合参数Table 2 Parameters of model describing the relationship between vertical wetting front and time intriangular profiles of homogeneous soil
注:a,b为模型拟合参数。

表3 均质三角形剖面斜面湿润锋与时间关系模型拟合参数Table 3 Parameters of model describing the relationship between inclined wetting front and time intriangular profiles of homogeneous soil
以往研究表明,湿润锋、入渗速率与时间一般呈幂函数关系(模型1)或与时间的0.5次方呈线性关系(模型2)[3-6]。将铅直面湿润锋与时间进行模型1和模型2拟合,发现铅直面湿润锋与时间呈极显著幂函数关系,决定系数R2均在0.94以上。图3显示,由模型1和模型2拟合的拟合值1、拟合值2与实测值均基本重合,拟合效果均佳。相关拟合参数如表2。
4.2 斜面湿润锋与时间的关系
同理,如图4所示,入渗初期,由于基质吸力为水分运动主要驱动力,水力梯度大,导致单位时间斜面湿润锋推进较快,表现为斜面湿润锋随时间变化曲线较陡,到入渗稳定时,由于重力作用逐渐成为主要驱动力,水力梯度趋于1,致使单位时间斜面湿润锋推进速度也趋于稳定,表现为斜面湿润锋随时间变化较平缓。
相同剖面入渗设置条件下,土样2的斜面湿润锋随时间推进速度快于土样1。同一质地紫色土,入渗前期,正三角形剖面斜面湿润锋随时间推进速度快于倒直角三角形剖面,但随入渗继续,反而逐渐慢于倒直角三角形剖面。
同理,将斜面湿润锋与时间进行模型1和模型2拟合,发现斜面湿润锋与时间呈极显著幂函数关系,决定系数R2均在0.97以上。图4显示,由模型1和模型2拟合的拟合值1、拟合值2与实测值均基本重合,拟合效果均佳。相关拟合参数如表3。

图4 均质三角形剖面斜面湿润锋与时间关系曲线Fig.4 Curves of inclined wetting front vs.time in triangular profiles of homogeneous soil
同时,将铅直面湿润锋与斜面湿润锋点绘图中,发现斜面湿润锋与铅直面湿润锋呈极显著线性关系,决定系数R2均在0.99以上,如图5所示。
正直角三角形剖面土样1和土样2拟合的线性关系分别为:
L=0.932 8Z+0.001 5, (R2=0.998 4);
(5)
L=0.888 8Z+0.011 8, (R2=0.990 2)。
(6)

图5 均质三角形剖面斜面湿润锋与铅直面湿润锋关系曲线Fig.5 Curves of inclined wetting front vs.vertical wetting front in triangular profiles of homogeneous soil
倒直角三角形剖面土样1和土样2拟合的线性关系分别为:
L=1.428 5Z+0.004 7,(R2=0.996 2) ;
(7)
L=1.355 9Z+0.010 1,(R2=0.991 7)。
(8)

表4 均质三角形剖面入渗速率与时间关系模型拟合参数Table 4 Parameters of model describing the relationship between infiltration rate and time intriangular profiles of homogeneous soil
4.3 入渗速率与时间的关系
图6和图7显示,入渗初期,由于基质吸力大,为水分运动主要驱动力,水力梯度大,单位时间入渗量较大,表现为累积入渗量和入渗速率随时间变化曲线较陡;到入渗稳定时,由于重力作用成为主要驱动力,水力梯度趋于1,致使单位时间入渗量也趋于稳定,表现为累积入渗量和入渗速率随时间变化曲线较平缓。
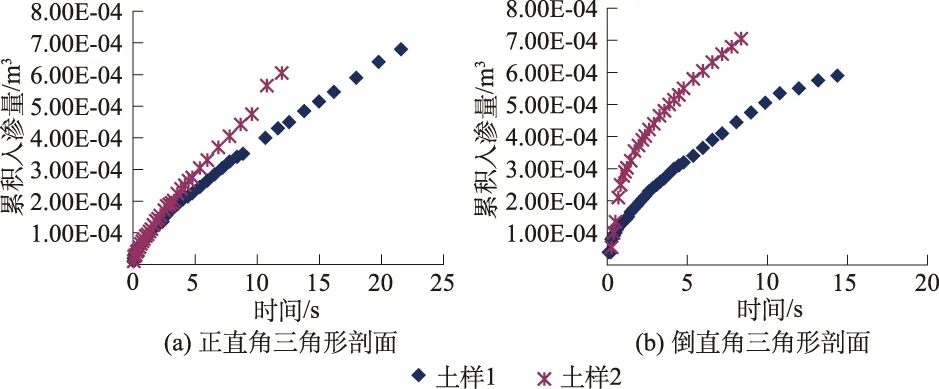
图6 均质三角形剖面累积入渗量与时间关系Fig.6 Relationships of cumulative infiltration vs. time in triangular profiles of homogeneous soil

图7 均质三角形剖面入渗速率与时间关系曲线Fig.7 Curves of infiltration rate vs.time in triangular profiles of homogeneous soil
相同剖面入渗设置条件下,质地越粗,大孔隙越多,单位时间土壤水分入渗越快,累积入渗量越大,图6和图7显示,一定时间,土样2的累积入渗量和入渗速度均大于土样1。同一质地,倒三角形剖面入渗速率快于正直角三角形剖面。
同理,将入渗速率与时间进行模型1和模型2拟合,发现入渗速率与时间呈极显著幂函数关系,决定系数R2均在0.94以上。图7显示,由模型1和模型2拟合的拟合值1、拟合值2与实测值均基本重合,拟合效果均佳。相关拟合参数如表4。
4.4 模型检验
由于模型表达式(2)和(3)中Ks,A,sinθ为常数项,式(2)和式(3)可简化为:
q=a+b/L;
(9)
q=a+b/Z。
(10)
式(9)中a=Ks×A,b=Ks×A×Sf/sinθ;式(10)中a=Ks×A,b=Ks×A×Sf。将实测入渗速率与斜面湿润锋、铅直面湿润锋数据对式(13)和式(14)进行拟合。结果显示,入渗速率与斜面湿润锋数的倒数、铅直面湿润锋数的倒数呈极显著线性关系,决定系数R2均在0.97以上,如图8所示。
正直角三角形剖面土样1和土样2其线性关系分别为:
q=1×10-8+2×10-9/L,(R2=0.998 3);
(11)
q=3×10-8+2×10-9/L,(R2=0.988 7)。
(12)
倒直角三角形剖面土样1和土样2其线性关系分别为:
q=2×10-8+1×10-9/Z,(R2=0.978 0);
(13)
q=2×10-8+5×10-9/Z,(R2=0.992 7)。
(14)

图8 均质三角形剖面入渗速率与铅直面(斜面)湿润锋关系曲线Fig.8 Curves of infiltration rate vs.vertical(inclined) wetting front in triangular profiles of homogeneous soil
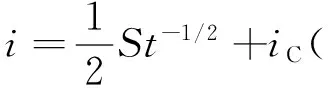
5 结 论
(1) 入渗初期,由于基质吸力为水分运动主要驱动力,水力梯度大,导致单位时间湿润锋推进较快,入渗量较大;到入渗稳定时,由于重力作用逐渐成为主要驱动力,水力梯度趋于1,致使单位时间湿润锋推进速度也趋于稳定,入渗量也趋于稳定。
(2) 粗质地的湿润锋随时间推进速度快于细质地。同一质地,正直角三角形剖面铅直面湿润锋随时间推进速度快于倒直角三角形剖面,但入渗速率小于倒直角三角形剖面;入渗前期,正三角形剖面斜面湿润锋随时间推进速度快于倒直角三角形剖面,但随入渗继续,反而逐渐慢于倒直角三角形剖面。
(3) 湿润锋、入渗速率与时间均呈极显著幂函数关系。
(4) 参考Green-Ampt入渗模式思路,首次建立了紫色土典型三角形均质剖面入渗模型。模型经实测值验证,模拟值与实测值具有非常好的一致性,充分说明了建立的入渗模型的可靠性和准确性,模型可用于描述紫色土特殊剖面构造的入渗过程。同时,建立的入渗模型可与经验模型相互转换,具有很好的一致性,模型参数也具有一定的物理意义。
[1] 朱显谟.再论黄土高原国土整治“28 字方略”[J].土壤侵蚀与水土保持学报,1995,1(1):4-11.(ZHU Xian-mo.The Restatement on the “28-Word General Plan” for the Loess Plateau’s Territory Rehabilitation[J].Journal of Soil Water Conservation,1995,1(1):4-11.(in Chinese))
[2] 王全九,邵明安,汪志荣,等.Green-Ampt公式在层状土入渗模拟计算中的应用[J].土壤侵蚀与水土保持学报,1999,5(4):66-70.(WANG Quan-jiu,SHAO Ming-an,WANG Zhi-rong,etal.Application of Green-Ampt Equation during Infiltration in Layered Soil[J].Journal of Soil Water Conservation,1999,5(4):66-70.(in Chinese))
[3] COLMAN E A,BODMAN G B.Moisture and Energy Conditions During Downward Entry of Water into Moist and Layered Soils[J].Soil Science Society America Proceedings,1945,(9):3-11.
[4] FOX Y S.One-dimensional Infiltration into Layered Soils[J].Journal of Irrigation and Drainage Engineering,1970,43:121-129.
[5] HILLEL D,BAKER R S.A Descriptive Theory of Fingering During Infiltration into Layered Soils[J].Soil Science,1988,146(1):51-56.
[6] HILL D E,PARLANGE J Y.Wetting Front Instability in Layered Soils[J].Soil Science Society America Proceedings,1972,36:697-702.
[7] 王文焰,张建丰,汪志荣,等.黄土中沙层对入渗特性的影响[J].岩土工程学报,1995,17(5):36-41.(WANG Wen-yan,ZHANG Jian-feng,WANG Zhi-rong,etal.Influence of Sand Loess on Infiltration Characteristics[J].Chinese Journal of Geotechnical Engineering,1995,17(5):36-41.(in Chinese))
[8] 王文焰,汪志荣,王全九,等.黄土中Green-Ampt入渗模型的改进与验证[J].水利学报,2003,(5):30-34.(WANG Wen-yan,WANG Zhi-rong,WANG Quan-jiu,etal.Improvement and Evaluation of the Green-Ampt Model in Loess Soil[J].Journal of Hydraulic Engineering,2003,(5):30-34.(in Chinese))
[9] GREEN W H,AMPT G A.Studies on Soil Physics,Flow of Air and Water Through Soils[J].Journal of Agricultural Science,1911,4(1):1-24.
(编辑:刘运飞)
Modelling the Water Infiltration in Typical TriangularProfile of Homogeneous Purple Soil
CHENG Dong-bing1,ZHENG Yan-xia2,QIAN Feng1,SUN Bei1
(1.Soil and Water Conservation Department,Yangtze River Scientific Research Institute,Wuhan 430010,China;2.Ecological Industrial Engineering Company Limited,Changjiang Institute of Survey,Planning,Design and Research,Wuhan 430010,China.)
The features of water infiltration in irregular profile of homogeneous purple soil was investigated by establishing an infiltration model of purple soil with reference to Green-Ampt theory.Profiles of right triangle and inverted right triangle of homogeneous purple soil are set through specialized soil infiltration test device indoor.Results reveal that the wetting front rate of coarse soil is faster than that of fine soil.For the same soil texture,the vertical wetting front rate in triangular profile is faster than that in inverted triangular profile,but the infiltration rate is smaller than that of inverted triangular profile.In the early stage of infiltration,the inclined wetting front rate in triangular profile is faster than in inverted triangular profile,and then gradually gets slower than inverted triangular profile.The wetting front,infiltration rate display obvious power function relationship with time.The established infiltration model was verified to be consistent with measured data.Meanwhile,it can be transformed with the existing empirical models,and the parameters are of physical meanings.
purple soil;triangular profile;soil infiltration;homogeneous soil;infiltration model
2015-01-09;
2015-01-16
国家自然科学基金项目(41201268);水利部科技推广资助项目(TG1419);长江科学院创新团队资助项目(CKSF2012052/TB)
程冬兵(1979-),男,江西乐平人,高级工程师,博士,主要从事水土保持与土壤水动力学研究,(电话)027-82829611(电子信箱)xiao2005zhu@163.com。
10.3969/j.issn.1001-5485.2015.03.010
S152.7
A
1001-5485(2015)03-0044-06
2015,32(03):44-49

