基于混合集合规划的作业车间生产排程模型研究

刘 轩，尚 鋆，白 翱

（中国工程物理研究院 机械制造工艺研究所，绵阳 621900）

0 引言

合理、有效的计划和排程是现代制造系统高效运行的关键所在之一。随着制造过程智能化的需求牵引，近年来对于作业车间的生产排程问题研究较多，其基本技术路线以智能计算方法的建模和求解为主，典型的算法包括遗传算法、禁忌搜索算法、粒子群算法、模拟退火算法等[1～4]。然而，工业生产中的排程问题往往属于NP-hard问题。具体而言，在实际的工程应用中，除了要考虑多约束、多目标的因素之外，还需要兼顾由制造资源种类多、加工工序数量大等导致的求解规模大的因素。此外，不同零件的加工工序数量、不同工序的加工工时大小都可能有很大的差别，且存在一定的不确定性，这些因素也都大大增加了问题求解的困难性，求解结果距离实际应用往往存在较大的差距。这使得目前的排程在很大程度上仍然依赖于人的经验，其合理性、有效性有待提升。

混合集合规划（Mixed Set Programming，MSP）[5]理论是一种在混合域上的、基于集合规划的算法体系，在处理工业上复杂的大规模组合优化问题时效果显著。近些年来，利用混合集合规划算法在铁路列车开行方案、航班计划恢复、路径优化等方面的研究较多[6～8]，相关应用及实践案例证明了该理论在求解多约束优化问题时的优势。自然约束语言（Natural Constraint Language，NCL）是由周建阳博士创建的、支持混合集合规划算法体系的语言系统[9]，它可以以一种人类更容易理解的方式来描述复杂的、变量间相互关联的工程优化模型。NCL支持隐式类型的声明、进行全局的语义分析、基于上下文的推理及求解。NCL将数值约束、简化的一阶逻辑及集合推理集成在一个语言环境之下，形成一个在混合域（实数、整数、布尔值、索引及集合）上针对约束满足问题的联合求解系统，最终获得工程优化问题的满意解。

针对多品种小批量生产模式下作业车间排程的难题，本文尝试将混合集合规划理论引入到作业车间生产排程问题的求解中。在分析和梳理作业车间资源、作业、工序约束的基础上，设置排程优化的主次目标，利用自然约束语言建立多约束优化模型，提出对应的求解策略并加以求解。研究结果将为复杂多约束条件下作业车间的排程优化提供一种新的手段和实现途径，从而辅助相关的计划调度人员进行科学和定量的决策。

1 作业车间生产排程问题的约束与目标

1.1 约束条件

作业车间生产排程是一个非常复杂的问题，本文将约束分为资源、作业、工序三类，其中资源指加工设备，作业指一种零件的一个加工批次。

1）资源层级约束

工作日历：资源可工作的时间集合。其中要考虑到周末、法定节假日、设备定期检修以及工作日的休息时间等资源不可工作时间。

资源占用：同一资源在任一时间只能加工一个零件的一道工序。

2）作业层级约束

最早开工时间：作业最早开始加工的时间。最早开工时间受制于任务下发时间、图纸及原材料到达时间、加工工序制定完成时间以及工装等的到位时间。

最晚完工时间：作业最晚完工的时间。一般以需求方要求的交货期限为准。

作业的优先级：不同的作业其优先级可能不同，优先级越高的作业加工次序越早。

3）工序层级约束

工序的工艺流程：要满足工序的基本加工次序。如工序2必须在工序1加工完成后才能开始加工。工序单次加工：一个零件的一道工序只能加工一次。工序的可用资源：可以完成一道工序的加工的所有资源的集合。

工序时间：工序的工时，包括工序的准备工时和实际加工工时。为了提高排程的实用性和准确性，将工序的检验工时和转运工时也增加到工序时间中。

1.2 优化目标

作业车间生产排程问题往往存在多个优化目标，本文将优化目标分为作业完工和资源利用两类。

1）作业完工类

最小化作业延迟时间总量；

最小化作业总完工时间；

最小化作业延迟总数量；

最大化作业按期完工率；

……

2）资源利用类

最大化瓶颈资源利用率；

最大化资源利用均衡率；

最大化资源总利用率；

最小化资源空闲总时间；

……

这些优化目标都是在生产排程中希望达到的效果，但事实上需要把优化目标分出主次，甚至有时候不同目标之间是相互冲突的，这时就需要牺牲掉一些次要目标，来保证主要目标的实现。NCL支持多目标优化，并以优化目标在程序中的自然顺序为优化顺序，也就是说，第一条优化目标为主优化目标，是要优先满足的，剩下的优化目标的优先性逐条降低。

2 建模及求解

2.1 建模思路

建模的基本思路如下：1）首先根据排程的基本要素建立相应的数据库，作为生产排程的基础数据；2）然后以数据库中的变量作为基础变量逐条建立约束条件模型；3）之后根据生产需要选取所需的优化目标；4）最后根据所选的优化目标设计相应的求解策略，从而实现优化求解。

建模思路框图如图1所示。

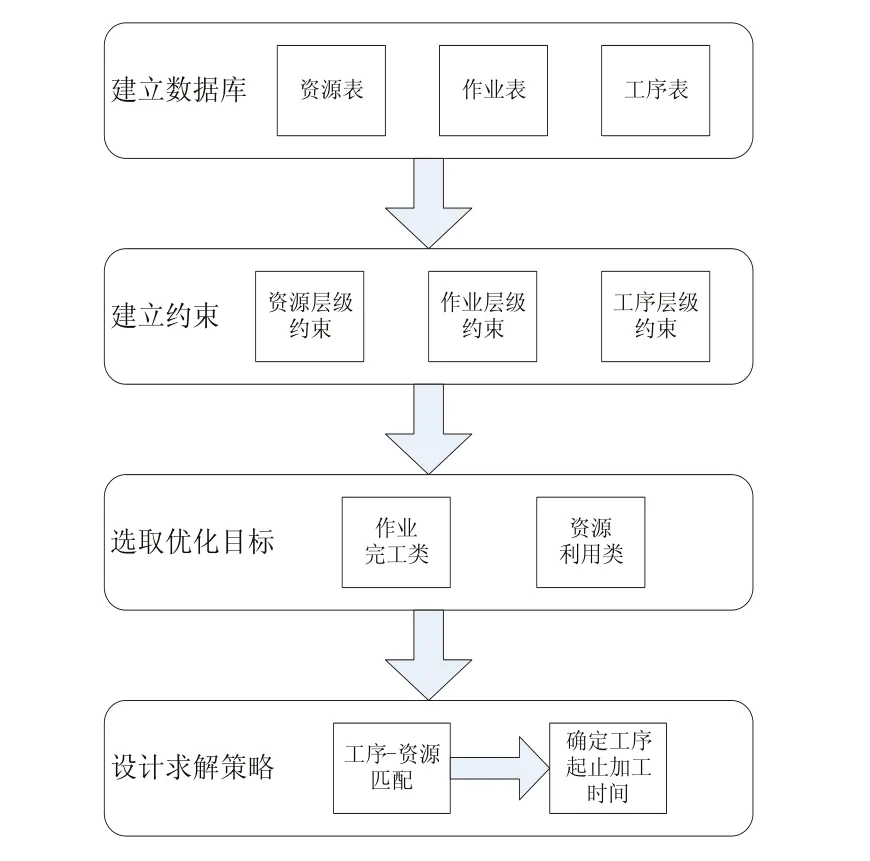
图1 建模思路框图

2.2 数据结构设计

建立生产排程的数据库，它包含三个基础表：资源（RESOURCE）、作业（JOB）、工序（TASK）。详细的数据结构分别如表1、表2、表3所示。

表1 资源表（RESOURCE）

表2 作业表（JOB）

表3 工序表（TASK）

2.3 约束模型的建立与详解

1）资源工作日历约束

对于不同的工序i和j，它们的加工时间不重叠，或者资源占用不同。

作业i的任何一个工序的开工时间都不能早于作业i的最早开工时间。

4）作业优先级约束

在实际的生产排程问题中，作业优先级是一个不容忽视的约束条件。作业的优先级越高，越要优先进行排程。在本文中将作业优先级分为三级：非常紧急、紧急、一般，分别对应数值2、1、0，数值越大优先级越高。

工序的优先级应与其对应的作业优先级保持一致，于是首先将作业优先级赋给其所有工序。之后，当工序i的优先级高于工序j的优先级，并且它们的资源占用发生冲突时，优先安排工序i。

5）工序工艺流程约束

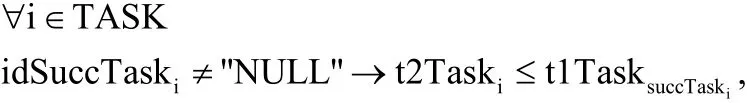
如果工序i的后继工序不为空，则工序i的完工时间不晚于工序i后继工序的开工时间。

6）工序单次加工约束

对于不同的资源i和j，一道工序如果安排在了资源i上，就不能再安排在资源j上。该道工序只能被加工一次。

2.4 优化目标的选取

这是次优化目标，在满足主优化目标的前提下满足此优化目标。

2.5 模型求解

运用混合集合规划算法对问题进行求解，其求解思想基于约束切割与深度优先搜索，根据选取的优化目标设计相应的求解策略有利于实现高效优化求解。本文中将求解过程分为两步，第一步将所有工序安排在相应资源上，第二步再确定每个工序的开工时间。

1）第一步

第二步以顺序性准则先后选取完工时间最早的工序和起始时间最早的工序，最后确定每个工序的开工时间。求解结束。

2.6 结果输出

最终排程结果可以以Excel表格形式和作业计划与延期统计表输出，也可以以可视化形式输出。图形可视化可以输出资源-工序甘特图、作业-工序甘特图、资源负载图。

3 应用实例

下面以某机加车间的实际生产数据进行应用实例验证。

该车间共有六大类资源，本文中抽象为A-F类。各类资源数分别为：A类16个（A01-A16），B类15个（B01-B15），C类8个（C01-C08），D类9个（D01-D09），E类21个（E01-E21），F类14个（F01-F14），总资源数共83个。选取的排程任务为开工时间在2015年1月内、完工时间在1月至3月内的157个作业，共596道工序。

运行环境：处理器为AMD Opteron™ Processor 6168 1.90GHz （双核处理器），安装内存（RAM）为32GB，Windows操作系统版本为Windows Server 2008 R2 Enterprise，POEM优化计算平台版本为Academic Vision 3.0。

求得可行解的时间为12分钟36秒。作业延迟时间总量为28682分钟，资源空闲时间总量为678974分钟。作业总完工时间为2015年03月09日12:58。排程结果能够满足实际生产的要求。

排程结果输出形式如下：

1）Excel表格形式

表格中详细列出了排程计划中每一道工序的开工时间和完工时间，以及加工资源、所属作业等信息，是排程结果的最基本表现形式。如图2所示。

2）作业计划与延期统计表

图2 Excel表格形式

该表统计了每个作业的原计划起止时间、计划完工时间和延期（天）信息。从表中可以看出，延期超过一天的作业一共有三个，它们的作业编号分别为93066_455789_858667、93400_458449_861018、93456_458760_860968，延期量分别为12天、3天和3天。可以通过协商调整交货日期或者将原作业进行批次划分来保证按期完工。如图3所示。

图3 作业计划与延期统计表

3）资源-工序甘特图

资源-工序甘特图按照资源排序，直观地显示了每一道工序的加工资源以及起止加工时间。图中还可显示工序的详细信息：所属作业、工序号、资源类别、资源实体、可替换资源、整道工序加工时间、加工时间跨度、作业应交付日期、件数、下道工序。通过该图还可以直观地看出每一个资源在各个时间段的加工任务，空闲时间较多的资源也一目了然。如图4所示。

图4 资源-工序甘特图

4）作业-工序甘特图

作业-工序甘特图按照作业排序，直观地显示了作业中每一道工序的起止加工时间。如图5所示。

图5 作业-工序甘特图

5）资源负载图

资源负载图显示了计划期内每一个资源设备的利用率，从而可以直观地了解车间资源利用的整体情况。从图中可以看出，共有12个资源的利用率超过了50%，其中更有5个资源的利用率达到了100%。如图6所示。

图6 资源负载图

4 结论

对作业车间的实际生产排程问题进行了建模与求解，除常规的生产排程约束条件外，又充分考虑了作业的优先级约束，使得求得的结果更加符合实际生产的要求。同时求解策略中对于瓶颈资源利用和资源利用均衡性的考虑，使得排程结果更加优化。表格及可视化的结果输出，对于实际生产起到了一定的指导作用，方便管理者尤其是计划调度人员进行合理的计划安排和任务下发，有利于提高制造过程的效率并提升设备利用率。

[1] 张国辉,高亮,李培根,张超勇.改进遗传算法求解柔性作业车间调度问题[J].机械工程学报,2009,45(7):145-151.

[2] 张超勇,高亮,李新宇,邵新宇.基于进化禁忌算法的Job-Shop调度问题研究[J].华中科技大学学报(自然科学版),2009,37(8):80-84+95.

[3] 彭传勇,高亮,邵新宇,周驰.求解作业车间调度问题的广义粒子群优化算法[J].计算机集成制造系统,2006,12(6):911-917+923.

[4] 潘全科,朱剑英.一类解决作业车间调度问题的遗传退火算法[J].聊城大学学报(自然科学版),2005,18(1):20-22+29.

[5] Jianyang Zhou.A Note on Mixed Set Programming[A].Proceedings of the Seventh International Symposium on Operations Research and its Applications. Lijiang, Asia-Pacific Operations Research Center, Academy of Mathematics and Systems Science, Chinese Academy of Sciences[C].2008:10.

[6] 熊星.基于混合集合规划的高速铁路列车开行方案优化研究[D].北京:北京交通大学,2012.

[7] 朱博.不正常航班飞机和机组计划恢复问题研究[D].南京:南京航空航天大学,2012.

[8] 白晓勇,周建阳.基于混合集合规划的车辆路径优化[J].物流技术,2009,28(7):171-173.

[9] 周建阳.自然约束语言[M].北京:科学出版社,2009.