给定最大度的极大拉普拉斯谱单圈偶图

林国光，宋海洲

（华侨大学数学科学学院，福建泉州362021）

给定最大度的极大拉普拉斯谱单圈偶图

林国光，宋海洲

（华侨大学数学科学学院，福建泉州362021）

摘要：通过图的移接变形对拉普拉斯谱半径的影响，研究了给定最大度为>2的n阶极大拉普拉斯谱单圈偶图的性质，得到了它的规范拉普拉斯谱向量中绝对值最大的分量对应的顶点的度均等于且这些顶点的位置均在圈上。

关键词：单圈偶图；最大度；拉普拉斯谱半径；移接变形；向量

作通者讯简作介者：宋海洲（1971—），男，副教授，主要研究方向为图论。

1　预备知识

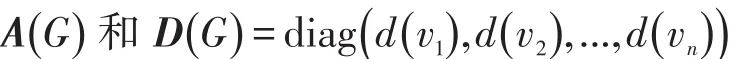
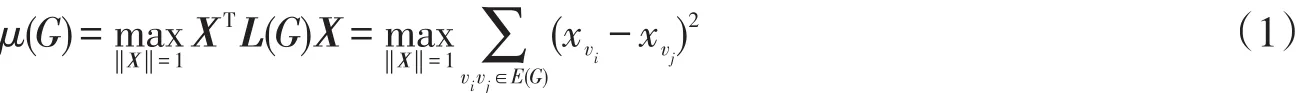
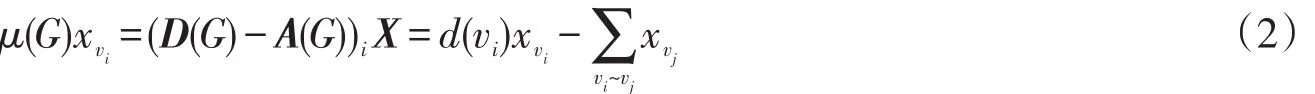
其中：(D(G)-A(G))i表示矩阵D(G)-A(G)的第i行；xvi,xvj分别表示X中对应于顶点vi,vj的分量；vi~vj表示顶点vi与顶点vj相邻接。

边数等于顶点数的简单连通图称为单圈图，圈长为偶数的单圈图称为单圈偶图。本文中用S=(V(S),E(S),C)表示单圈偶图，其中C为S中的唯一圈；用(u,v)表示E(S)中的一条边，简记uv。其中u,vV(S)；用S-uv表示从S中删去边uvE(S)所得到的图，用S+uv表示从S中添加边uvE(S)所得到的图，其中u,vV(S)；用NS(v)表示S中所有与顶点v相邻的顶点构成的集合；用d(u,v)表示在S中的顶点u到顶点v的距离；用(S)表示S的最大度，简记为(>2)；用表示最大度为的n阶单圈偶图构成的集合。

图的拉普拉斯谱半径是图谱理论的重要研究课题之一。1986年Brualdi和Solheid［2］提出了一个关于图的谱半径问题：对于一个给定图的集合，确定该集合中图的谱半径的上界（或下界），并刻画该上界（或下界）的极图。近年来在极图刻画方面的研究有很大的进展：如郭继明等［3］和刘慧清等［4］分别研究了在给定直径条件下树和单圈图中谱半径最大的极图；张晓东［5-6］研究了给定度序列的条件下树和单圈图取得拉普拉斯谱半径和拟拉普拉斯谱半径最大的极图；冯琳等［7］刻画出固定围长的单圈图的无符号拉普拉斯谱极图等等。本文研究给定最大度为>2的n阶极大拉普拉斯谱单圈偶图的性质，得出它的规范拉普拉斯谱向量中绝对值最大的分量对应的顶点的度均等于且这些顶点的位置均在圈上。

2　基本定义及引理

本节先给出后面证明主要结论时将要用到的一些定义及引理。

定义1设S=(V(S),E(S),C)是一个单圈偶图。若L(S)的特征向量X=(xv)vV(S)满足‖X‖=1，且(S)=XTL(S)X，则称X为S的一个规范拉普拉斯谱向量［8］。

引理1［9］设G=(V1,V2;E)是含有n个顶点的偶图，V1={v1,v2,...,vj}，V2={vj+1,vj+2,..., } vn，V(G)=V1⋃V2，V1⋂V2=且G中的每条边都连接V1中一点和V2中一点。令X为G的一个规范拉普拉斯谱向量，则sgn(xv1)=…=sgn(xvj)=-sgn(xvj+1)=…=-sgn(xvn)0，其中sgn()表示实数的符号。

引理2［9］（嫁接变形）设u,v是连通偶图G=(V1,V2;E)的两个互不相同的顶点，且NG(v) NG(u){u} ={v1,v2,…,vs}(1≤s≤d(v))。记G*是由G删除边vvi，同时添加边uvi(1≤i≤s)后所得到的连通偶图（见图1）。设X是G的一个规范拉普拉斯谱向量，若|xu|≥|xv|，则(G)<(G*)。

引理3［5］（交叉移接变形）设u1,u2,v1,v2是简单连通偶图G=(V(G),E(G))的四个互不相同的顶点，且v1与u1相邻，v1与v2不相邻，v2与u2相邻，u1与u2不相邻。记G*是由G删除边v1u1，v2u2，同时添加边v1v2,u1u2后所得到的简单连通偶图（见图2）。设X是G的一个规范拉普拉斯谱向量，若|xv1|≥|xu2|且|xv2|≥

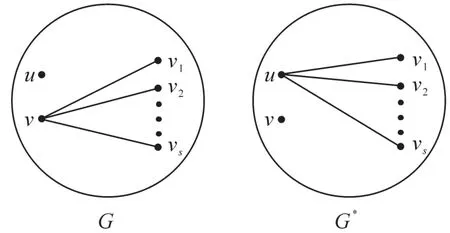
图1　偶图G和偶图G*Fig.1 Bipartite graph G and G*

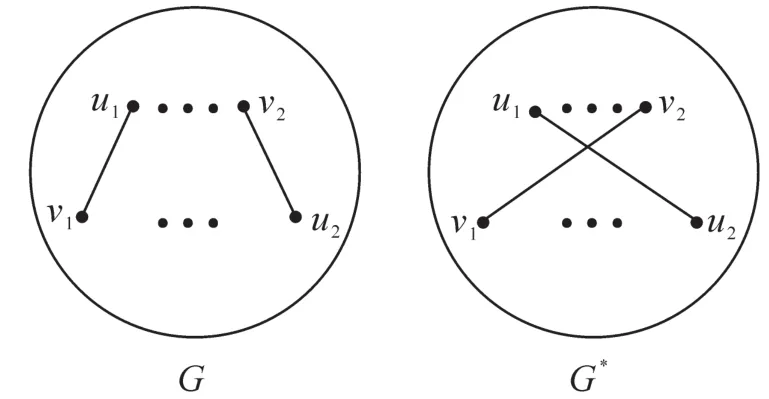
图2　简单连通图G和G*Fig.2 Simple connected graph G and G*

引理4［10］设G是一个顶点阶数n≥2的简单连通图，则(G)≥+1，等号成立当且仅当=n-1，其中(G)为L(G)的最大特征值，为G的最大度。

引理5设S*是中的一个含有叶子顶点的极大拉普拉斯谱单圈偶图，X是S*的一个规范拉普拉斯谱向量。设uk是S*中的一个叶子顶点，uk-1NS*(uk)，则|xuk|<|xuk-1|。

故引理5成立。

引理6设S*是中的一个极大拉普拉斯谱单圈偶图，X是S*的一个规范拉普拉斯谱向量，顶点u,v是同时在S*的圈上或圈外。若d(u)>d(v)，则|xu|>|xv|。

证明反证法。假设若d(u)>d(v)且有|xu|≤|xv|成立。因为d(u)>d(v)，从而在NS*(u) NS*(v){v}中一定存在d(u)-d(v)个点，不妨设为u1,…,ud(u)-d(v)，使得S1=S*- uu1-…-uud(u)-d(v)+vu1+…+ vud(u)-d(v)仍为单圈偶图，则易知S1。由|xv|≥|xu|，利用引理2可知(S1)>(S*)，与S*的定义矛盾。故引理6成立。

由引理6可以得到如下推论。

推论1设S*是中的一个极大拉普拉斯谱单圈偶图，X是S*的一个规范拉普拉斯谱向量，顶点u,v是同时在S*的圈上或圈外。①若|xu|>|xv|，则d(u)≥d(v)；②若|xu|=|xv|，则d(u)=d(v)。

3　主要结果及其证明

定理1假设S*是中的一个极大拉普拉斯谱单圈偶图，C是S*中的唯一圈，X是S*的一个规范拉普拉斯谱向量。则X中绝对值最大的分量对应的顶点的度均等于。

证明反证法。假设S*中存在一个顶点v*使得|xv*|=max{|xv||vV(S*)}，d(v*)<，记k=d(v*)。在S*中任取一个度为的顶点u，即d(u)=。下面对k的大小分以下三种情形讨论。

情形1当k=1时

则顶点v*必为叶子顶点，取wNS*(v*)，由引理5可知|xv*|<|xw|与|xv*|=max{|xv||vV(S*)}矛盾。

情形2当k=2时

对于情形2，根据顶点u,v*在S*中的位置分以下三种情形讨论。

情形2.1当顶点u,v*同时在圈上或圈外时

因为d(u)>d(v*),|xu|≤|xv*|，与引理6矛盾。

情形2.2当顶点u在圈外且顶点v*在圈上时

情形2.3当顶点v*在圈外且顶点u在圈上时

对于情形2.3，根据顶点v*离圈上最近的顶点是不是u分以下两种情形讨论。

情形2.3.1顶点v*离圈上最近的顶点不是u

情形2.3.2顶点v*离圈上最近的顶点是u

则取v1NC(u)，令S3=S*-uv1+v1v*，下面对S3圈长的奇偶性进行讨论。

32C141224v*v1知(S4)>(S*)，与S*的定义矛盾。

若S3的圈长为偶数，则S3，由|xv*|≥|xu|，利用引理2可知(S3)>(S*)，与S*的定义矛盾。

5(S*)，与S*的定义矛盾。

情形3当k≥3时

综上所述情形讨论，可知假设不成立，故定理1成立。

u0v若u0V(C)，设u0u1…uk(k≥1)是一条在圈外长度为k的路且uk为叶子顶点。若存在w1V(C)，有|xw1|≤|xuk|成立。则存在使得(S)>(S)成立。1

证明由定理1可知d(u0)=，由引理5可知|xuk|<|xuk-1|。记w*为圈中到u0的最近的顶点，取w2NC(w1){w*}，令S1=S-w1w2+w2uk，下面对图S1的圈长的奇偶性分以下两种情形讨论。

情形1当S1的圈长为偶数时

1ukw11

情形2当S1的圈长为奇数时

综上所述情形，可知引理7成立。

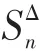
证明反证法。假设X中绝对值最大的分量对应的顶点中存在一个顶点u0的位置在圈外。则可知在S*中存在一条长度为k的路u0u1…uk使得顶点u0,u1,…,uk均不在圈上且uk为叶子顶点，由引理7的逆否命题可知在S*中对任意vV(C)均有|xv|>|xuk|成立。由定理1可知|xu0|=max{|xv||vV(S*)}，则d(u0)=。设圈上的顶点按顺时针排列为v1,v2,…,v2t-1, v2t…,v2m,v1(1≤t≤m,2≤m,t,mN+)，且v2m是圈中离u0最近的顶点（见图3），记l=d(u0,v2m)，则d(uk-1,v2m)= k-1+l，其l≥1,k≥1,l，kN+。下面对k的大小分以下三种情形讨论。

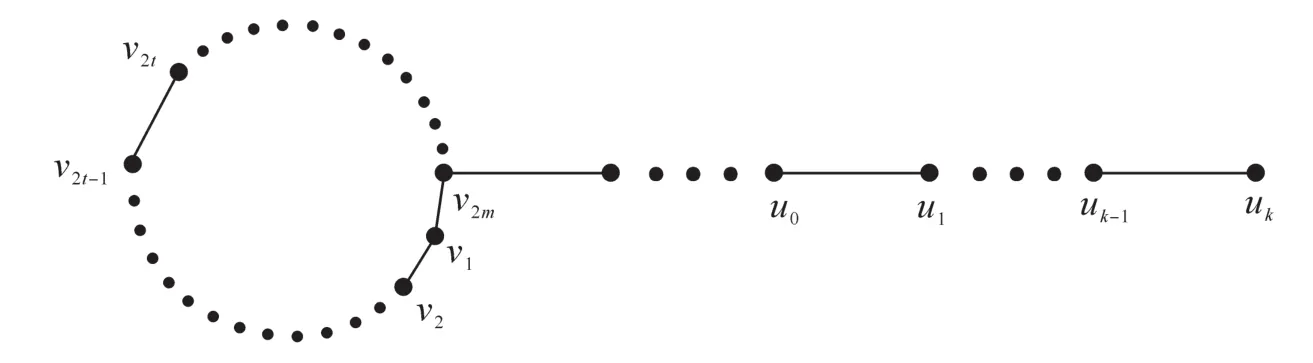
图3顶点v2m是圈中离圈外顶点u0最近的一顶点

Fig.3 Vertex v2mon the circle is closest to vertex u0outside the circle

情形1当k=1时

则d(uk-1,v2m)=l，下面对l的奇偶性进行讨论。

情形1.1当l为奇数时

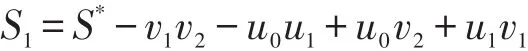
情形1.2当l为偶数时

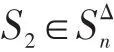
情形2当k=2时

则d(uk-1,v2m)=l+1，下面对l+1的奇偶性进行讨论。

情形2.1当l+1为奇数时

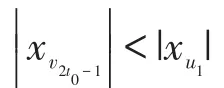
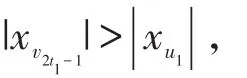
情形2.2当l+1为偶数时

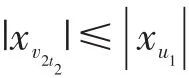
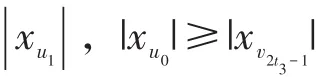
情形3当k≥3时

则d(uk-1,v2m)=k-1+l，下面对k-1+l的奇偶性进行讨论。

情形3.1当k-1+l为奇数时

对于情形3.1，根据k的奇偶性进行讨论。

情形3.1.1当k为偶数时，设k=2i,i≥2,i,j,pN+。

1）当j=1时，可证对任意的t均有|xv2t-1|>|xuk-1|与|xv2t|>|xuk-2|成立。

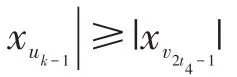
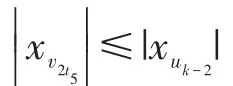
2）假设p|xuk-(2j-1)|与|xv2t|>|xuk-2j|成立。

3）则可证当j=p+1时，对任意的t均有|xv2t-1|>|xuk-(2p+1)|与|xv2t|>|xuk-(2p+2)|成立。

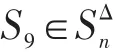
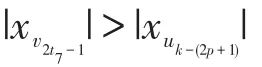
由数学归纳法可知，对任意的t均有|xv2t|>|xuk-2i|成立，即有|xv2t|>|xu0|成立，与u0的定义矛盾。

情形3.1.2当k为奇数时，设k=2i-1,i≥2,i,j,pN+。

1）当j=1时，类似情形3.1.1可证对任意的t均有|xv2t-1|>|xuk-1|与|xv2t|>|xuk-2|成立。

2）假设p|xuk-(2j-1)|与|xv2t|>|xuk-2j|成立。

3）当j=p+1时，则与情形3.1.1类似可证任意的t均有|xv2t-1|>|xuk-(2p+1)|成立，且若k> 2p+2，对任意的t均有|xv2t|>|xuk-(2p+2)|成立。

由数学归纳法可知，对任意的t均有|xv2t-1|>|xuk-(2i-1)|成立，即有|xv2t-1|>|xu0|成立，与u0的定义矛盾。

情形3.2当k-1+l为偶数时

当k为偶数时，则与情形3.1.1类似可证对任意的t均有|xv2t-1|>|xu0|成立；当k为奇数时，则与情形3.1.2类似可证对任意的t均有|xv2t|>|xu0|成立。但这都与u0的定义矛盾。

综上所述情形讨论，可知假设不成立，故定理2成立。**，易知

参考文献：

[1] CVETKOVI D, DOOB M, SACHS H. Spectra of Graphs-Theory and Applications[M]. New York: Academic Press, 1980:58-75.

[2] BRUALDI R A, SOLHEID E S. On the spectral radius of complementary acyclic matrices of zeros and ones[J].SIAM J Algebra Discrete Methods, 1986(7):265-272.

[3] GUO J M, SHAO J Y. On the spectral radius of trees with fixed diameter[J]. Linear Algebra and itsApplications,2006,413(1): 131-147.

[4] LIU H Q, LU M, TIAN F. On the spectral radius of unicyclic graphs with fixed diameter[J]. Linear Algebra and its Applications, 2007,420(2/3):449-457.

[5] ZHANG X D. The Laplacian spectral radii of trees with degree sequences[J].Discrete Mathematics, 2008,308(15):3143-3150.

[6] ZHANG X D. The signless Laplacian spectral radius of graphs with given degree sequences[J]. Discrete Applied Mathematics, 2009,157(13):2928-2937.

[7]冯琳,姚艳红,郭继明,等.具有固定围长的单圈图的无符号拉普拉斯谱半径[J].高校应用数学学报, 2011,26(1):121-126.

[8]汪秋分,宋海洲.图的拉普拉斯谱半径对应的特征向量的性质及应用[J].华侨大学学报:自然科学版, 2014,35(1):107-111.

[9] GUO J M. The effect on the Laplacian spectral radius of a graph by adding or grafting edges[J]. Linear Algebra and its Applica⁃tions, 2006,413(1):59-71.

[10] MERRIS R. Laplacian matrices of graphs: a survey[J]. Linear Algebra and its Applications, 1994(197/198):143-176.

（责任编辑姜红贵）

On the Unicyclic Bipartite Graphs of Maximal Laplacian Spectrum with Given Maximum Degree

Lin Guoguang, Song Haizhou
(School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China)

Abstract:By considering the effect of adding and grafting edges to a graph on the Laplacian spectral radius, this paper studies the properties of maximal Laplacian spectrum unicyclic bipartite graphs with order n and the given maximum degree>2 , and concludes that the component of the normalized Laplacian vector which has the larg⁃est absolute value is corresponding to a vertex of degree, and this vertex is on the circle.

Key words:unicyclic bipartite graph; maximal degree; Laplacian spectrual radius; grafting; vector

作者简介：林国光（1988—），男，硕士研究生，主要研究方向为图论。

基金项目：福建省自然科学基金项目（2011J05005）；中央高校基本科研业务费专项资金资助项目（10HZR26）

收稿日期：2014-12-26

文章编号：1005-0523（2015）03-0126-07

中图分类号：O157.5

文献标志码：A