非达西流动对致密砂岩气藏压裂水平井产能的影响

袁 淋，李晓平

（1.中国石化西南油气分公司川东北采气厂，四川 阆中 637042；2.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610500）

非达西流动对致密砂岩气藏压裂水平井产能的影响

袁 淋1，李晓平2

（1.中国石化西南油气分公司川东北采气厂，四川 阆中 637042；2.西南石油大学油气藏地质及开发工程国家重点实验室，四川 成都 610500）

致密砂岩气藏储层非达西渗流特征使得其不同于常规气藏，准确预测致密砂岩气藏压裂水平井产能至关重要。基于致密砂岩气藏压裂水平井渗流机理，考虑应力敏感、滑脱效应、气体高速非达西流以及井筒压降对产能的影响，定义气体广义拟压力，建立了致密气藏储层—裂缝—井筒耦合产能计算新模型。实例分析表明，利用新模型计算无阻流量结果与产能测试结果相对误差仅为3.08%，相对误差较小，说明新模型具有较高的准确性。研究表明，随着裂缝条数、裂缝半长以及滑脱因子的增大，无阻流量增大，而随着应力敏感指数的增大，无阻流量逐渐减小，且井底流压较小时更加明显。研究为致密气藏压裂水平井流入动态研究以及裂缝参数优化设计提供了理论依据。

致密砂岩气藏；压裂水平井；应力敏感；滑脱效应；高速非达西；井筒压降

随着全球油气资源形势的逐渐严峻，页岩气、煤层气以及致密砂岩气等非常规天然气资源越来越受到人们的关注[1-2]，其中致密砂岩气的勘探与开发技术最为成熟，但由于其低孔、低渗以及低含气饱和度等特征，通常采用水平井辅加压裂措施来提高气井产量。目前，国内外学者致力于致密砂岩气藏成藏机理、渗流特征以及开发技术等方面的研究[3-5]，而对致密砂岩气藏压裂水平井流入动态研究较少，国内宁正福[6]、孙福街[7]、徐梦雅[8]以及张德良[9]等人虽对低渗、致密砂岩气藏压裂水平井产能进行了充分的研究，但均没有考虑致密气藏储层实际渗流特征。在综合考虑应力敏感、滑脱效应、气体高速非达西流以及水平井筒压降的基础上，利用势叠加原理推导出致密砂岩气藏压裂水平井流入动态计算新模型，并利用产能测试结果验证了新模型的可靠性，同时分析了裂缝参数以及地层参数对产能的影响，为致密砂岩气藏压裂水平井产能预测提供了新的思路。

1 致密气藏压裂水平井产能公式推导

1.1 物理模型

假设水平井位于顶底封闭，水平方向无限大均质致密砂岩气藏中，储层厚度为h，储层渗透率为K，水平井段长度为L，井筒半径为rw，水平井分段压裂后压开N条等长度、等间距分布裂缝，裂缝穿透整个储层，裂缝半长为Xf，裂缝渗透率为Kf，裂缝宽度为w，压后水平段无补孔，储层流体首先由储层流向水力裂缝，再经裂缝流入水平井井筒，最终由水平井井筒趾端流入跟端。对于不同裂缝条数的压裂水平井，其物理模型以及井筒管流模型如图1、2所示。

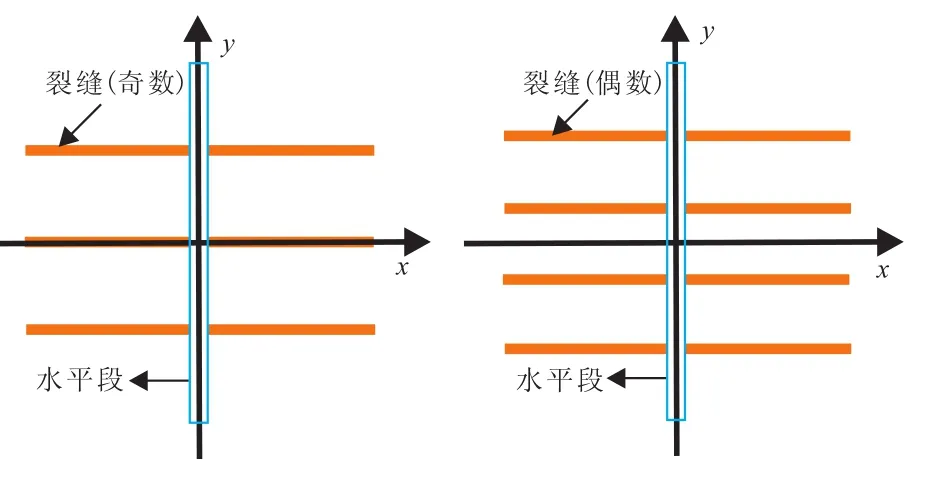
图1 压裂水平井物理模型Fig.1 Physical model of fractured horizontal well

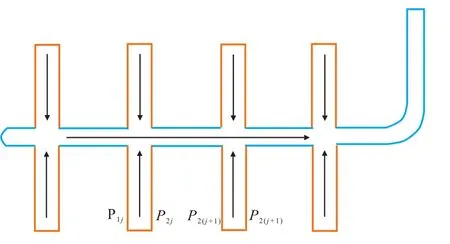
图2 压裂水平井井筒管流模型Fig.2 Conduit flow model of fractured horizontal well

1.2 数学模型

1.2.1 地层渗流模型

在油藏中，压裂水平井投产时，任一条裂缝在裂缝周围产生的压力分布为[10]：

式中：p(x，y)为裂缝周围任一点的压力分布，MPa；qo为油井产量，m3/d；μo为原油黏度，mPa·s；Bo为原油体积系数；K为储层绝对渗透率，10－3μm2；h为储层厚度，m；Xf为裂缝半长，m。

式（1）左右两边同时微分，并将其化为气藏条件下的微分表达式得[11]：

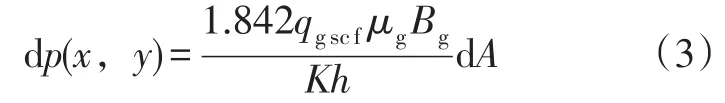
式中：qgscf为裂缝流量，m3/d；μg为天然气黏度，mPa·s；Bg为天然气体积系数。

在致密砂岩气藏中，由于气体滑脱效应[12]以及应力敏感的[13]影响，式（3）可以表示为：

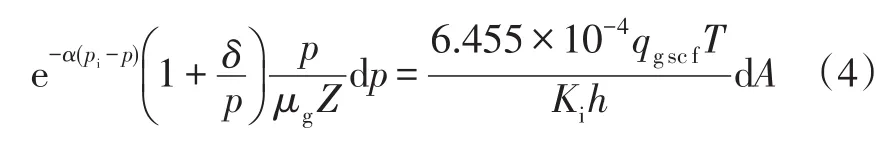
式中：δ为滑脱因子，MPa；Ki为储层原始渗透率，10－3μm2；α为应力敏感指数，MPa-1；pi为原始地层压力，MPa；Z为天然气偏差因子；T为储层温度，K。

定义气体广义拟压力：

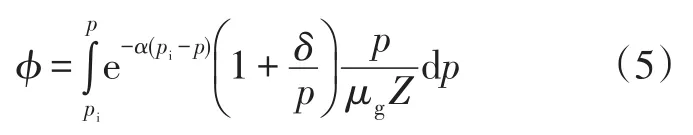
式（4）两边同时积分，并考虑N条裂缝相互干扰，则任一条裂缝周围广义拟压力分布为：

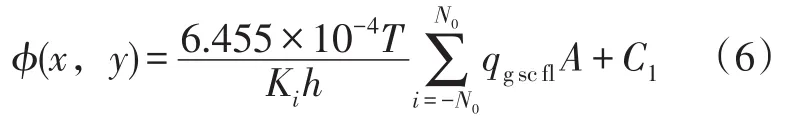
若裂缝条数为奇数，i从-N0以1的速度递增；若裂缝条数为偶数，i从-N0以2的速度递增，且裂缝间距或半间距d以及l与N0的表达式为：

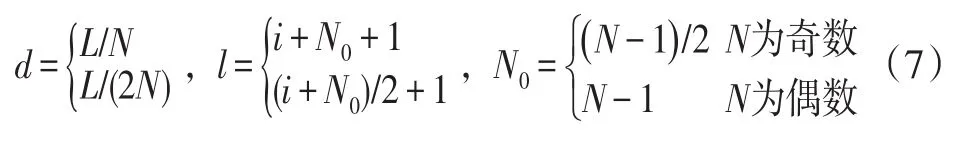
式中：d为裂缝间距或半间距，m；L为水平段长度，m；N为裂缝条数。

将第j条裂缝中部坐标（0，md）以及泄气边界处坐标（0，re）代入式（6），联立两式并根据

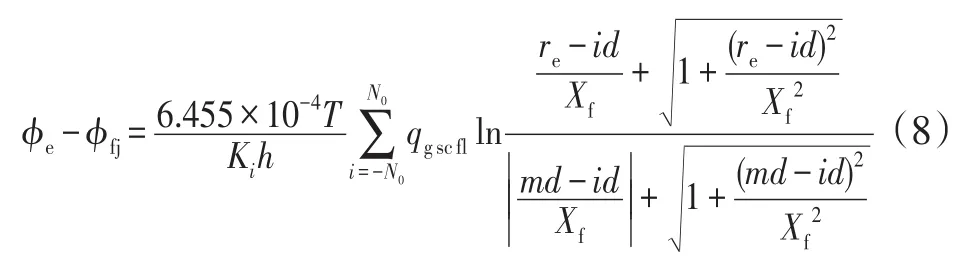
1.2.2 裂缝渗流模型

对于任一条裂缝，气体由裂缝流入井筒的过程可看成是储层厚度为裂缝宽度w，泄气半径为h/2，供给边界压力为pfj，井筒半径为rw的平面径向渗流，则裂缝中运动方程为：

式中：qgfj为任一条裂缝地下流量，m3/d；Kf为裂缝渗透率，10－3μm2；ρg为天然气密度，g/cm3；β为紊流系数，m-1；w为裂缝宽度，m。

将体积系数Bg、气体密度ρg以及紊流系数β的表达式代入式（9）中得：

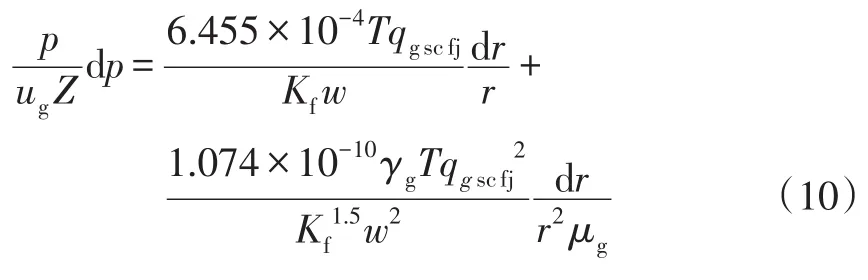
式中：γg为天然气相对密度。

根据气体拟压力定义，式（10）两边同时积分得到气体在裂缝中的产能公式：

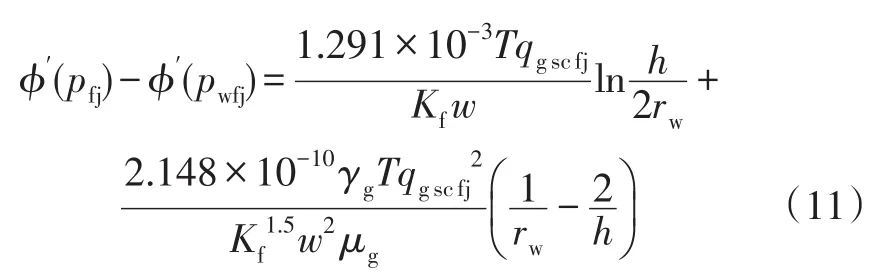
式中：pwfj为任一条裂缝中部压力，MPa；pfj为任一条裂缝尖端压力，MPa；rw为水平井筒半径，m。

1.2.3 井筒管流模型

当气体由水平井筒趾端流向跟端，由于井筒摩擦效应以及流体汇流效应，井筒中将产生一定程度的压降。任取一条裂缝，如图2所示，当气体由第j条裂缝左端流到第j+1条裂缝右端过程中，由动量定理得到摩擦压降和加速度压降分别为：

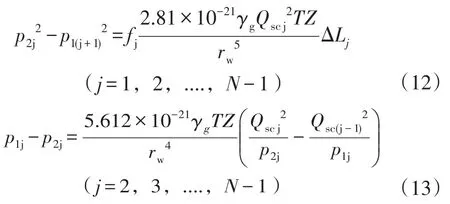
式中：p1j为第j条裂缝左端压力，MPa；p1(j+1)为第j+1条裂缝左端压力，MPa；fj为第j段井筒摩擦系数；p2j为第j条裂缝右端压力，MPa；ΔLj为两裂缝左端的距离，m；Qscj为第j段井筒中总流量，m3/d；Qsc(j-1)为第j-1段井筒中流量，m3/d。

其中fj为摩擦系数，其表达式为：

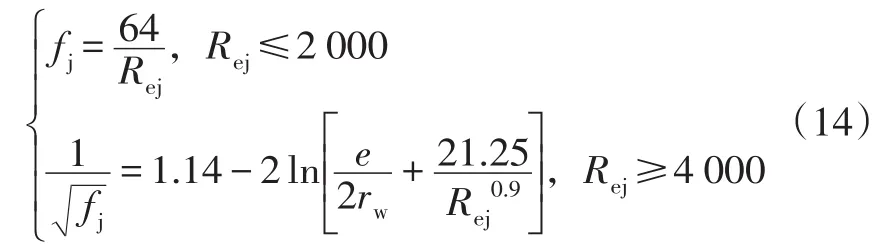
式中：Rej为第j段井筒中雷诺数；e为井筒粗糙度，m。Qscj为第j段井筒内气体的流量以及相邻裂缝左端的距离ΔLj为：

对于趾端裂缝处，由于无汇流影响，因此：

1.2.4 模型求解

将地层渗流模型式（8）、裂缝渗流模型式（11）以及井筒管流模型式（12）、式（13）以及式（16）联立即可得到压裂水平井每条裂缝的产量以及总产量，具体求解步骤为：

1）先假定一组裂缝的产量初值（qscfj初值最好不为0），将其代入式（12）、式（13）以及式（16），利用跟端压力逐次逆行计算初始条件下井筒压力分布：p2N，p1N，…，p11，并计算各裂缝中部压力pwfj=(p1j+p2j)/2。

2）将计算得到的裂缝中部压力pwfj代入式（8）、式（11），联立两式得到含2N个未知数、2N个非线性方程的非线性方程组，利用拟牛顿法迭代计算方程组的解，得到每条裂缝新的产量值qscfj以及裂缝尖端压力pfj。

3）比较计算得到的累计产量以及初始累计产量，若两者差值满足一定的误差范围，则假设初始产量即为真实产量；若不满足误差范围，将计算得到新裂缝产量作为初值，重复以上两步工作，直到满足一定的精度，迭代停止，压裂水平井总产量即为QscN。

2 实例计算及影响因素分析

2.1 实例计算

某致密砂岩气藏中一压裂水平井参数如下：水平井段长度L为435 m，水平井筒半径rw为0.1 m，井筒粗糙度e为0.000 15 m，储层厚度h为30 m，储层原始地层压力pi为28 MPa，目前地层压力pe为27.56 MPa，供给半径re为500 m，储层原始渗透率Ki为0.1× 10－3μm2，气藏温度T为340.8 K，天然气相对密度γg为0.76，压裂后裂缝条数N为3条，裂缝半长Xf为30 m，裂缝宽度w为0.005 m，裂缝渗透率Kf为30 μm2，实验测得储层应力敏感指数α为0.05 MPa-1，气体滑脱因子δ为0.5 MPa，该井产能测试无阻流量为10.743 2×104m3/d。

利用以上实例参数，根据式（8）、式（11）、式（12）、式（13）以及式（16），分别计算各种假设条件下压裂水平井无阻流量，并与产能测试无阻流量进行对比，如表1所示。

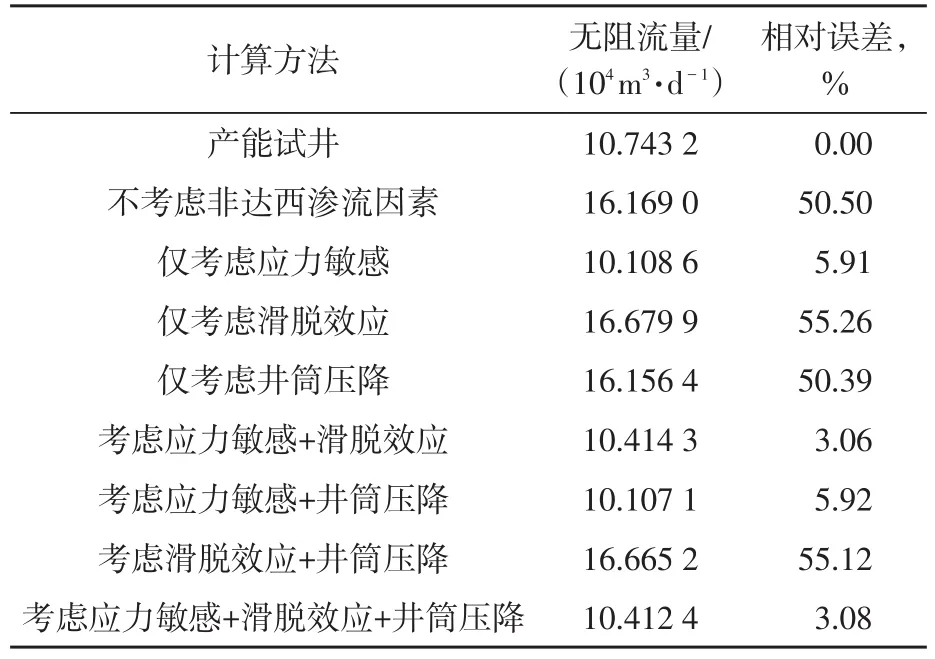
表1 无阻流量计算结果对比Table 1 AOF calculation result contrast

由表1可以看出，同时考虑应力敏感与滑脱效应条件下，利用理论方法计算无阻流量的结果与实际产能测试无阻流量相对误差较小，这就表明新公式具有较高的准确性。同时也可以看出，应力敏感对压裂水平井产能影响较为明显，使得无阻流量下降50%，气体滑脱效应对产量具有较小的影响，而水平井井筒压降对产量基本无影响，在实际产能研究过程中可忽略不计。

2.2 致密气藏压裂水平井流入动态影响因素分析

2.2.1 裂缝条数对流入动态的影响

当其他参数一定时，作不同裂缝条数N条件下的压裂水平井流入动态曲线（图3），由图3可以看出，随着裂缝条数N的不断增大，IPR曲线右移，无阻流量增大，但是增加的趋势越来越缓慢，最终将趋于一个稳定的值。这是因为虽然裂缝条数的增加增大了渗流面积，但同时裂缝间的干扰也变强，两个因素共同作用使得无阻流量的增加越来越缓慢。在对致密砂岩气藏水平井进行压裂设计时，应合理优化裂缝条数，既能保持较高的产量，也能达到最优的经济效益。

2.2.2 裂缝半长对流入动态的影响

图3 裂缝条数对流入动态的影响Fig.3 Influence of fracture number on IPR

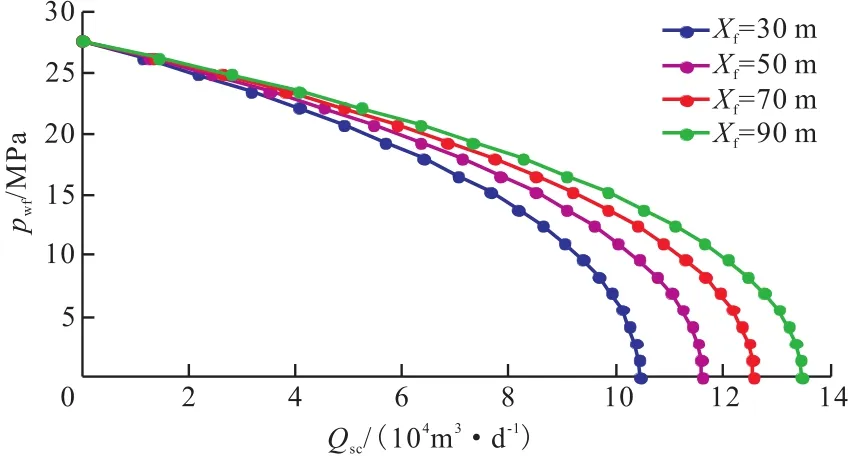
图4 裂缝半长对流入动态的影响Fig.4 Influence of fracture half lengths on IPR

当其他参数一定时，作不同裂缝半长Xf条件下的压裂水平井流入动态曲线（图4），由图4可以看出，随着裂缝半长Xf的逐渐增大，IPR曲线右移，无阻流量增大，且增大的趋势逐渐平缓。这是因为裂缝半长Xf的增大虽然提供了更大的渗流面积，而裂缝间的干扰也有所加剧，但相比裂缝条数增加引起的缝间干扰相对较小。因此，在致密砂岩气藏水平井进行压裂设计时，在考虑经济效益的前提下，可尽量增加裂缝半长。

2.2.3 应力敏感对流入动态的影响

当其他参数一定时，作不同应力敏感指数α条件的压裂水平井流入动态曲线可以看出，不考虑应力敏感时（α=0），压裂水平井产量较考虑应力敏感（α≠0）条件下的产量偏大，且随着应力敏感指数α的增大，IPR曲线左移，无阻流量减小，尤其是生产压差较大时，应力敏感对产量的影响更加明显。这是因为应力敏感指数越大，地层越容易被压实，渗透率降低的程度更大，进而产量降低，因此，对于强应力敏感储层，在开发过程中应合理控制生产压差。

2.2.4 滑脱效应对流入动态的影响

当其他参数一定时，作不同滑脱因子δ条件下压裂水平井流入动态曲线可以看出，不考虑滑脱效应（δ=0）时，压裂水平井产量小于考虑滑脱效应（δ≠0）下的产量，且随着滑脱因子的逐渐增大，IPR曲线右移，无阻流量增大，尤其是井底压力较低时，滑脱效应对无阻流量的影响更加明显。这是因为滑脱效应的存在增大了气相渗透率，且井底压力较低时，气相渗透率增加的幅度更大，但考虑到井底压力较低时，应力敏感较强，因此，生产过程中应合理控制生产压差，既能保持明显的滑脱效应，又能削弱应力敏感。

3 结论

1）基于致密气藏压裂水平井渗流机理，综合考虑应力敏感、滑脱效应、气体高速非达西流以及井筒压降的影响，定义气体广义拟压力，推导出了致密气藏压裂水平井地层渗流—裂缝渗流—井筒管流的耦合模型。实例分析表明，利用新公式计算无阻流量结果与产能测试结果相对误差较小，说明新公式具有较高的准确性和实用性。

2）敏感性分析表明，随着裂缝条数、裂缝半长以及滑脱因子的增大，IPR曲线右移，无阻流量增大，而随着应力敏感指数的增大，IPR曲线左移，无阻流量减小。在致密气藏压裂水平井压裂设计以及开发过程中应综合考虑各个因素的影响，合理高效开发致密气藏。

[1]邱中建，邓松涛.中国非常规天然气的战略地位[J].天然气工业，2012，32（1）：1-5.

[2]Chen Dongxia,Wang Lei,Pang Xiongqi,et al.Geological characteristics and hydrocarbon accumulation models of the tight-sand gas reservoirs in Upper Triassic Xujiahe formation in western Sichuan depression of China[C].SPE 16891,2013.

[3]黄志龙，柳波，闫玉魁，等.吐哈盆地柯柯亚—鄯勒地区致密砂岩气形成机制与分布预测[J].岩性油气藏，2011，23（2）：15-19.

[4]吴娟娟，李仲东，陈威，等.大牛地气田太2段致密砂岩气层识别研究[J].岩性油气藏，2013，25（1）：102-106.

[5]李新豫，曾庆才，包世海，等.“两步法反演”技术在致密砂岩气藏预测中的应用——以苏里格气田苏X区块为例[J].岩性油气藏，2013，25（5）：81-85.

[6]宁正福，韩树刚，程林松，等.低渗透油气藏压裂水平井产能计算方法[J].石油学报，2002，23（2）：68-71.

[7]孙福街，韩树刚，程林松，等.低渗气藏压裂水平井渗流与井筒管流耦合模型[J].西南石油学院学报，2005，27（1）：32-36.

[8]徐梦雅，廖新维，何逸凡，等.完井方式对致密气藏压裂水平井产能的影响[J].油气地质与采收率，2012，19（2）：67-71.

[9]张德良，张烈辉，赵玉龙，等.低渗透气藏多级压裂水平井稳态产能模型[J].油气地质与采收率，2013，20（3）：107-110.

[10]郎兆新，张丽华，程林松.压裂水平井产能研究[J].石油大学学报（自然科学版），1994，18（2）：43-46.

[11]陈志海，马新仿，郎兆新.气藏水平井产能预测方法[J].天然气工业，2006，26（2）：98-99.

[12]Klinkenberg L J.The permeability of porous media to liquid and gases[M]//Drilling and Production Practice,Washington,D C：American Petroleum Institute,1941.

[13]Farquhar R A,Smart B G D,Todd A C.Stress sensitivity of low-permeability sandstones from the rotliegendes sandstone [C].SPE 26501,1993.

（编辑 杨友胜）

Influence of non-Darcy flow on productivity of fractured horizontal wells in tight sandstone gas reservoir

Yuan Lin1and Li Xiaoping2
(1.NortheastSichuanGasProductionPlant,SinopecSouthwestOilandGasCompany,Langzhong,Sichuan637402,China;2.State KeyLaboratoryofOilandGasReservoirGeologyandExploitation,SouthwestPetroleumUniversity,Chengdu,Sichuan610500,China)

The non-Darcy seepage characteristic makes tight sandstone gas reservoir be different from conventional gas reservoir. It is important to accurately predict productivity of fractured horizontal wells in tight sandstone gas reservoir.According to percolation mechanism,considering the influence of stress sensitivity,slippage effect,high velocity non-Darcy and wellbore drawdown on productivity,gas generalized pseudopressure is defined.Moreover,new productivity calculation model of reservoir,fracture,wellbore coupling in tight sandstone gas reservoir is established.Example analysis shows that compared with productivity test results, relative error is only 3.08%by using this new model.The small error indicates that this new model has good accuracy.Research shows that as the increasing of fracture number,fracture half length and slippage factors,absolute open flow(AOF)increases.However,as the increasing of stress sensitivity index,the AOF decreases,especially when bottom hole flowing pressure(BHFP)is low. The researches provide theoretical basis for studying inflow performance relationship(IPR)and fracture parameter optimization of fractured horizontal wells in tight sandstone gas reservoir.

tight sandstone gas reservoir,fractured horizontal well,stress sensitivity,slippage effect,high velocity non-Darcy, wellbore drawdown

TE375

：A

2015-04-20。

袁淋（1990—），男，硕士研究生，油气藏渗流力学以及油气藏工程。

教育部“长江学者和创新团队发展计划”（IRT1079）。