包络变形对阶比分析结果的影响及消除方法

程卫东， 王天杨， Wang Jin-jiang， Robert X Gao， 温伟刚， 李建勇

(1.北京交通大学机械与电子控制工程学院， 北京 100044；2.康涅狄格大学机械工程系 斯托斯 CT 06269 美国)

包络变形对阶比分析结果的影响及消除方法

程卫东1， 王天杨1， Wang Jin-jiang2， Robert X Gao2， 温伟刚1， 李建勇1

(1.北京交通大学机械与电子控制工程学院， 北京 100044；2.康涅狄格大学机械工程系 斯托斯 CT 06269 美国)

转速变化的滚动轴承故障诊断通常先采用计算阶比跟踪技术消除变转速的影响，再进行阶比分析获得故障特征。然而，等角度重采样会引起冲击包络变形进而导致阶比分析结果产生偏差，在转速变化范围较大时这个偏差必须要受到重视。介绍了等角度重采样方法，仿真了包络变形对阶比分析结果的影响，给出了峰值点间隔变化量详细的理论推导，提出了通过修正角度变换值来消除包络变形影响的方法，并进行了实验验证。研究结果显示，包络在宽窄方向的变形对阶比分析结果没有影响；相邻包络峰值点间隔的变化对阶比分析结果产生影响；在角度序列逐点减去峰值点间隔变化量可消除包络变形对阶比分析结果的影响。

故障诊断； 滚动轴承; 计算阶比跟踪； 角域重采样； 包络变形

1 概 述

在机械、能源、石化、运载和国防等行业，间歇性工作的机械设备普遍存在、量大面广。例如矿用电铲(一种大型挖掘机)，它用铲斗以间歇重复的工作循环进行工作。一个工作循环由挖掘、满斗回转至卸载地点、卸载、空斗回转至挖掘地点4个工序构成。工作节拍是提升机构配合推压机构完成铲装动作，回转机构配合行走机构完成卸料动作，每个工作节拍之间有一定的时间间隔。各工作部的传动机构间歇性工作，齿轮箱中的轴及滚动轴承转速变化不定，以静止-升速-转速波动持续-降速-静止的变化状态工作。该类设备上的轴承几乎没有恒定的转速，并且转速变化范围大。对这类设备上的滚动轴承进行故障诊断，必须要从转速大范围变化并且频繁启停工况下的振动信号中提取故障特征[1-4]。

滚动轴承故障产生的振动信号已经被广泛研究[5-8]，共振解调技术[9]及其改进技术[10-11]由于实用有效而被广泛使用。包络分析方法是40多年前提出的滚动轴承故障诊断的基础方法，滚动轴承的故障诊断技术发展至今，很多技术或方法都是围绕包络分析方法的改进和提高。包络分析法的核心是先对振动信号进行带通滤波，带通滤波的频带选择采用小波变换[12]和谱峭度[13]等技术。滤波后进行幅值解调获得包络信号，再对其进行频谱分析得到故障特征信息。然而，这些技术仅适用于轴承在恒定转速的工况。在变转速工况下，需要使用计算阶比跟踪技术来去除转速变化的影响[14-18]。计算阶比跟踪和包络分析法结合的集成方法被提出来用于变转速工况下滚动轴承的故障诊断[3,19]。集成方法的流程如图1所示，转速的变化引起故障冲击包络疏密变化，不能直接对其进行频谱分析。使用计算阶比跟踪技术，即利用转速信息和插值算法对包络信号进行等角度重采样得到同步包络信号。对同步包络信号的谱分析(称为阶比分析)才可以得到变转速轴承的故障特征。

图1 计算阶比跟踪与包络分析集成方法Fig.1 Flow chart of integrative envelope analysis and computed order tracking

然而，针对滚动轴承的故障信号使用计算阶比跟踪技术有一定的特殊性。在实现等角度重采样时，首先需要设定一个转速参考基准。如果参考基准设定为转速变化范围的最小值，那么等角度重采样时要增加采样点；如果参考基准设定为转速变化范围的最大值，则等度角重采样时会减少采样点。对于实际诊断系统来说，选择转速的最小值作为参考基准更切实可行，这样可以避免因减少采样点带来的包络信息的丢失风险，又不至于实际转速意外超出由转速最大值确定的参考基准而发生错误。

采用增加采样点的方法(即设定转速的最小值作为参考基准)，不同转速时所插数据点数不同会导致包络发生变形。也就是说，冲击包络的峰值点与该包络的起始点之间被拉长或被压缩，引起相邻包络峰值点之间的间隔变化,进而影响阶比分析的结果[20]。

针对这个问题，本文的主要工作是研究包络变形对后续阶比分析结果的影响因素及规律，并进一步提出消除方法。

2 滚动轴承故障冲击响应与轴承转速的关系

对包络进行频谱分析时，包络峰值之间的间隔决定着包络周期性出现的频率，包络形状及峰值的大小影响周期分量的振幅值。对于变化转速滚动轴承的故障产生的包络，需要知道故障包络与变化的转速之间的关系。

2.1 故障冲击包络峰值与转速的关系

图2显示的冲击响应信号是在Machinery Fault Simulator实验平台上获得，是滚动轴承在900 r/min转速时外圈单点故障产生的冲击响应。定义峰值Amax所在时刻与包络开始时刻之间的时间为包络上升时间tr；峰值与包络衰减为零时刻之间的时间为衰减持续时间tf。

包络峰值Amax体现了冲击能量的大小，而冲击能量大小受故障点通过轴承载荷区速度的影响[5]，即同一个故障点转速快时激发的包络峰值要大于转速慢时激发的包络峰值。

图2 滚动轴承外圈单点故障的冲击响应Fig.2 Waveform of fault impulse response

2.2 包络上升时间与转速的关系

滚动轴承变转速运行时，同一个故障点引发的两次相邻冲击处于不同的转速工况，决定了这两次冲击具有不同的冲击能量。利用Machinery Fault Simulator实验平台，获得轴承外圈单点故障转速在600～2 400 r/min之间的7种稳定转速下的响应信号(采样频率24 kHz)，统计各种转速时的包络上升时间。由于转速的快慢影响本底噪声水平，统计时以0.05 V做为门槛电压，该门槛与包络的交叉点记为冲击响应的开始时刻。每一种转速选择10个相邻的冲击包络来计算平均的包络上升时间。统计结果见表1所示。

表1 不同转速时包络上升时间统计

Tab.1 Statistical analysis of peak time under different rotational speed

轴承转速/(r·min-1)上升时间/s均值/s标准差/s6000．087089000．0859612000．0875815000．085790．086510．0006318000．0865421000．0862924000．08629

由各转速下上升时间的统计结果看，滚动轴承在600～2 400 r/min转速范围产生的故障冲击包络的上升时间虽然各不相同，但是没有明显的变化趋势，各转速下的均值为0.086 51 s，标准差为0.000 63 s。由冲击能量与响应上升时间的理论分析可以得到同样结论(本文略)。故在后文推导过程假设不同转速下冲击响应的包络上升时间不变。

3 角域重采样引起的包络变形

3.1 等角度重采样方法

等角度重采样之前，时间轴是描述时域信号的横轴，单位为s。时域振动信号数据点之间是等时间间隔Δt为

(1)

式中fst为时域采样频率，单位为Hz。

等角度重采样之后，角度轴是重采样之后用于描述角域信号的横轴，单位设为r。时间到角度的转换采用下式

(2)

式中φ表示t时间内轴承所转过的角度，通过轴承实时转速对时间的积分求得。n(t)为轴承的实时转速，单位为r/min。

利用角域数据点构建三次样条曲线，再对该曲线进行等角间隔重采样。在等角度重采样处理过程中，设定最低转速nmin为参考基准。在最低转速时轴承每转过一周的采样点数等同于时域采样频率，就可保证重采样满足采样定理，角域重采样频率fsφ由下式确定

(3)

式中fsφ为角域采样频率，单位为“1/r”。重采样之后角度轴上数据点之间的角度间隔Δφ为

(4)

从上述描述可见，由于实际转速都高于参考基准，所以重采样后角域数据点数多于原时域数据点数，并且转速高的数据段重采样之后的数据点数多于转速低的数据段的数据点数，导致了不同转速时不同程度的包络变形。

3.2 等角度重采样仿真

如图1所示，故障引起的振动冲击最终体现为包络解调之后的上半周包络信号。为了说明对包络进行等角度重采样产生的包络变形，采用三角波模拟冲击包络进行仿真。仿真时设轴承旋转一周均匀出现5个冲击包络，轴承转速均匀上升时，起始转速60 r/min，加速度为40 r/s2；轴承转速均匀下降时，起始转速600 r/min，加速度-40 r/s2。因为冲击包络的发生只和轴承转过的角度有关，所以包络的起点在旋转一周内均布。图3(a)是转速由低向高变化的时域包络图，包络的起点在时间轴上出现的位置由疏到密变化，包络的宽度不变；图3(c)是转速由高向低变化的时域包络图，包络起点位置由密到疏变化，包络的宽度不变。图3(b)是图3(a)经过等角度重采样后的角域包络图，图3(d) 是图3(c)经过等角度重采样后的角域包络图。

从图3(b)可见，在加速工况下等角度重采样后包络起点均匀分布在角度轴的一周之内，包络的波形随着转速升高被逐渐拉宽，并且随着包络波形变宽峰值点也相对右移,相邻包络峰值点的间隔也逐渐变大。图3(d)所示的减速工况，包络的波形随着转速降低逐渐被压窄，并且相邻峰值点的间隔逐渐变小。

图3 转速上升、下降时等角度重采样仿真Fig.3 Simulation in different domain during speed-up and speed-down

4 包络变形对阶比分析结果的影响

角域重采样时引起的包络变形体现在两方面：(1)包络横向被拉宽或压窄；(2)峰值点间隔逐渐变大或变小。仿真时采用三角波模拟故障引起的冲击包络，转速均匀上升时，加速度为40 r/s2，起始转速60 r/min，等角度重采样后的角域信号包含了包络横向被拉宽并且峰值点间隔逐渐变大的因素，如图4(c)所示。转速下降时，减速度为-40 r/s2，起始转速600 r/min，等角度重采样后的角域信号包含了包络横向被压窄并且峰值点间隔逐渐变小的因素，如图4(d)所示。把图4(c)和(d)两图中包络的峰值点移成等间隔分布，对应成图4(a)和(b)，分别只含有包络横向被拉宽或压窄的因素，峰值点间隔相同。

图4 不同的包络变形Fig.4 The different envelope deformation

对图4的4种包络做FFT计算，即阶比分析，结果见图5所示。观察峰值点间隔相同的(a)和(b)两条包络的阶比分析结果，故障特征峰都出现在5阶比处，横向变形没有影响特征频率。看(c)和(d)两条包络的阶比分析结果，故障特征峰出现在4.82和5.13阶比处，说明包络峰值点间隔逐渐变大使得阶比分析结果变小，而峰值点间隔逐渐变小导致阶比分析结果变大。仿真研究结果显示，包络峰值点间隔逐渐变大或变小影响特征在频率轴上的位置，而包络拉宽或压窄只影响特征幅值大小。

图5 针对图4的不同变形包络的阶比分析结果Fig.5 Order analysis on different envelope deformation

5 相邻包络峰值点间隔的变化量

考虑到变化转速滚动轴承在实际诊断中只取一小段信号来分析，故设轴承转速以恒加速度均匀变化，并设相邻的两个包络上升时间tr相同。如图6所示，第1个冲击起始点所在角度为φ1，对应的时刻为t1，瞬时转速为n1；峰值点所在角度为φ3，对应的时刻为t3，转速为n3。峰值点与起始点之间的关系表示为：

(5)

(6)

(7)

图6 相邻包络起点和峰值点相互关系Fig.6 Relationship between adjacent impulses

随后到达的冲击包络起始点所在角度为φ2，对应的时刻为t2，实时转速为n2。由于包络起始点的出现只与轴承转过的角度有关，所以，相邻冲击起点位置间隔就是一个不变的角度φc(见图6所示)。第2个冲击与第1个冲击的相互关系：

(8)

(9)

相邻冲击间隔角为

(10)

由公式(9)和(10)，可以得出新的关系

(11)

第2个冲击包络的峰值点所在角度为φ4，对应的时刻为t4，实时转速为n4，峰值点和起点之间的关系为

t4=t2+tr

(12)

参照公式(7)和(11)，t4时刻对应的角度为

(13)

根据公式(7)和(13)，可以求出两个相邻包络峰值点的间隔

(14)

根据公式(14)，可以得出包络峰值点的间隔与包络起点的间隔存在差异

(15)

即，由于包络变形引起了相邻峰值间隔的角度变化量为Δφc。相对变化量表示为

(16)

由上述理论分析可知，如果包络的起点等间隔分布，则第2个包络与第1个包络的峰值点间隔增大Δφc，第3个包络与第1个包络的峰值点间隔增大量的计算要将2φc代入式(15)，即

可见峰值点间隔的增大呈非线性。公式(15)显示了引起包络变形的具体因素，即轴承的瞬时转速、加速度、相邻包络的间隔和包络的上升时间。通过公式(15)还可以看到，如果上升时间tr为零，包络峰值点间隔的变化量就为零，这也正是其他的研究认为故障冲击时间很短可以忽略，当成一个瞬间脉冲来处理的结果。公式(15)显示当转速变化范围大并且变化剧烈时，加速度及瞬时转速对包络变形有很大影响，所以包络上升时间tr不能忽略。

由公式(16)可以得出结论：加速度大(转速变化剧烈)，包络峰值点间隔变化大；加速度小(转速变化缓慢)，包络峰值点间隔变化小。加速度为正时(升速阶段)包络峰值点间隔逐渐变大；加速度为负时(降速阶段)包络峰值点间隔逐渐变小。瞬时转速小(低转速段)包络峰值点间隔变化大，瞬时转速大(高转速段)包络峰值点间隔变化小。

6 计算阶比跟踪方法改进

由上文第4小节的分析可知，包络峰值点间隔的变化是影响阶比分析结果的直接原因。本文的第5小节的理论分析结论是包络峰值点间隔的变化量与瞬时转速、加速度、相邻故障冲击的间隔和冲击包络的上升时间这4个因素有关。在研究方法的改进时，要依据理论分析结果去除包络峰值点间隔的变化量。

在图7中，与时轴上的时刻t1～t6对应的转速分别为n1～n6。按照上文分析的公式(13)有

(17)

(18)

(19)

比较上述3个公式发现，可以把各式减去峰值点间隔的变化量

图7 时域角域变换对照Fig.7 Adjacent impulses between time-domain and angle-domain

(20)

式中φc=0。

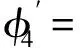
(21)

(22)

根据公式(20)，(21)和(22)，可以得到各相邻峰值之间的间隔

(23)

即，每个数据点的角度减去峰值点间隔变化量之后，可以保证重采样后包络峰值点间隔等同于起点间隔，即如果包络起点间隔是固定值，那么包络峰值点间隔也是固定值。

改进后计算阶比跟踪方法的实现步骤为：1)采用公式(2)作时间到角度的转换；2)每个数据点的角度减去公式(15)描述的变化量；3)利用角域数据点构建三次样条曲线，对该曲线进行等角间隔重采样。

7 实验验证

为了验证上述的理论分析，在实验台上测得滚动轴承的振动信号。轴承的转速由静止上升到2 400 r/min然后再下降到静止状态，其中的加速度和减速度的平均值为3.021 58 r/s2。实验平台(如图8所示)是SpectraQuest公司生产的Machinery Fault Simulator实验台。转速信号通过电机输出轴上的鉴相装置(旋转一圈产生一个光电脉冲)获得。轴承故障类型是外滚道单点损伤，轴承型号为 MB ER-10K，故障特征频率fBPFO=3.028×转轴频率。使用NI-PCI 6259数据采集系统采集振动信号和转速信号，采样频率24 kHz。

图8 实验平台Fig.8 Experimental setup

对振动数据去均值处理,并进行6～12 kHz的带通滤波，采用希尔伯特法进行包络解调获得包络信号。对包络信号进行等角度重采样，设nmin=30 r/min为参考基准，故角域采样频率为4 800 (1/r)。对重采样后的角域包络做短时傅里叶变换计算(STFT)，窗口宽度为7 200数据点。

在转速上升时计算了4段数据，4段数据对应的转速分别是984，1 830，2 028，2 226 r/min。从图9(a)可以看到，在转速由低到高变化过程中，故障特征的阶比值从2.86逐渐接近理论值3.028。可以证明加速上升时(加速度为正)，阶比结果小于匀速时的阶比结果。

在转速下降时也计算了4段数据，4段数据对应的转速分别是2 331，2 163，1 951和1 145 r/min。从图9(b)可以看到，在转速由高到低变化过程中，故障特征的阶比值从接近理论值3.028逐渐增加到3.24。可以证明减速下降时(加速度为负)，阶比结果大于匀速时的阶比结果。并且，图9(a)和(b)两图还可以证明低转速时阶比结果的偏差大，高转速时阶比结果的偏差小。

与图9(a)的数据处理过程相同，根据本文第6小节的修正方法，设定包络上升时间为0.086 51 s(依据前文的实验结果)，加速度为3.021 58 r/s2，相邻包络的间隔为1/3.028 r，在角度转换时减去变化量Δφc，再进行等角度重采样，STFT计算结果(阶比分析结果)见图8(c)所示。984， 1 830， 2 028和2 226 r/min 4种转速时对应数据段的阶比分析结果都落在了理论值3.028处。减速下降工况的修正效果同图9(c)(略)，验证了修正方法的有效。

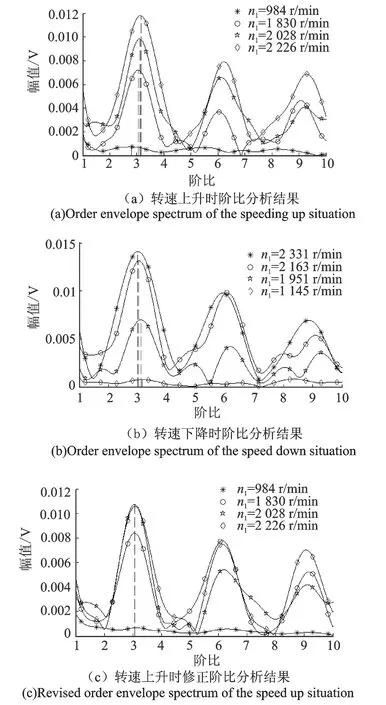
图9 实验数据的阶比分析结果Fig.9 The order analysis results of the tested vibration signal

8 结 论

针对等角度重采样过程中的包络变形问题，本文分析了包络变形对后续阶比分析结果的影响因素及影响规律，并给出了影响的消除方法。

影响因素有4个，分别是加速度、瞬时转速、包络的上升时间和相邻包络的间隔。与滚动轴承工况相关的加速度及瞬时转速两个因素对阶比分析结果的影响规律是：(1)与恒定转速下的阶比分析结果相比，加速度大(转速变化剧烈)，阶比分析结果的偏差大；加速度小(转速变化缓慢)，阶比分析结果偏差小。加速度为正时(升速阶段)分析结果小于恒定转速时的阶比分析结果；加速度为负时(降速阶段)分析结果大于恒定转速时的阶比分析结果。(2)瞬时转速对阶比分析结果的影响是在低转速段上阶比分析结果偏差大，在高转速段上阶比分析结果偏差小。

消除方法的原理是调整变形后包络峰值点的间隔，在数据点从时域转换到角域时引入一个去除项，仿真及实验结果验证了该方法的有效性。

对转速大范围变化并且频繁启停工况下的滚动轴承进行故障诊断时，通常使用计算阶比跟踪技术来去除转速变化的影响，然后再对等角度采样信号做进一步的频谱分析。本文研究成果的意义在于，描述了阶比跟踪时包络变形对后续的阶比分析结果的影响因素及规律，并且给出了消除方法，使得计算阶比跟踪和包络分析相结合的集成方法更为准确，对于这类工况下滚动轴承的故障诊断具有实际意义。

致谢:感谢美国康涅狄格大学机械工程系EMS实验室对本文实验的支持，特别感谢Robert X Gao教授及WANG Jinjiang博士对于本文成文的指导和修改。

[1] Amirata Y, Benbouzida M E H, Al-Ahmar E, et al. A brief status on condition monitoring and fault diagnosis in wind energy conversion systems[J]． Renewable and Sustainable Energy Reviews, 2009， 13:2 629—2 636.

[2] Cheng W, Wang T, Wen W, et al. Anomaly detection for equipment condition via frequency spectrum entropy[J], Advanced Materials Research, 2012, 433-440: 3 753—3 758.

[3] Wang J, Gao R, Yan R. A hybrid approach to bearing defect diagnosis in rotary machines[J]. CIRP Journal of Manufacturing Science and Technology, 2012,5: 357—365.

[4] Tadina M, Boltezar M. Improved model of a ball bearing for the simulation of vibration signals due to faults during run-up[J]. Journal of Sound of Vibration, 2011， 330(17):4 287—4 301.

[5] Randall R， Antoni J. Rolling element bearing diagnostics-A tutorial[J]. Mechanical Systems and Signal Processing, 2011，25: 485—520.

[6] Yan R， Gao R. Approximate entropy as a diagnostic tool for machine health monitoring[J]． Mechanical Systems and Signal Processing, 2007，21: 824—839.

[7] Sinha J K， Elbhbah K, A future possibility of vibration based condition monitoring of rotating machines[J]． Mechanical Systems and Signal Processing, 2013,34: 231—240.

[8] Jamaludin N, Mba D. Monitoring extremely slow rolling element bearings: part I[J]． NDT & E International, 2002,35: 349—358.

[9] McFadden P D， Smith D D. Vibration monitoring of rolling element bearings by the high-frequency resonance technique-a review[J]. Tribology International,1984，17: 3—10.

[10]Tandon N， Choudhury A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings[J]. Tribology International, 1999，32: 469—480.

[11]Sheen Y T. A complex filter for vibration signal demodulation in bearing defect diagnosis[J]．Journal of Sound and Vibration,2004，276: 105—119.

[12]Yan R. Gao R, Multi-scale enveloping spectrogram for vibration analysis in bearing defect diagnosis[J]． Tribology International, 2009， 42: 293—302.

[13]Antoni J， Randall R B. The spectral kurtosis: application to vibratory surveillance and diagnostics of rotating machines[J]． Mechanical System and Signal Processing, 2006, 20: 308—331.

[14]Borghesani P, Pennacchi P, Randall R B, et al. Order tracking for discrete-random separation in variable speed conditions[J]． Mechanical Systems and Signal Processing, 2012,30: 1—22.

[15]Wang K, Heyns P. Application of computed order tracking Vold-Kalman filtering and EMD in rotating machine vibration[J]. Mechanical Systems and Signal Processing, 2011,25: 416—430.

[16]Fyfe K, Munck E. Analysis of computed order tracking[J]. Mechanical Systems and Signal Processing, 1997,11: 187—205.

[17]Brandt A, Lagö A, Ahlin K， et al. Main principles and limitations of current order tracking methods[J]. Sound and Vibration, 2005,39(3): 19—22.

[18]Saavedra P N, Rodriguez C G. Accurate assessment of computed order tracking[J]. Shock and Vibration, 2006，13: 13—32.

[19]Luo H G, Qiu H, George G, et al. Synthesized synchronous sampling technique for differential bearing damage detection[J]． ASME Journal of Engineering for Gas Turbines and Power, 2010，132: 1—16.

[20]Cheng W, Gao R, Wang J, et al. Envelope deformation in computed order tracking and error in order analysis[J]. Mechanical System and Signal Processing, 2014,48:92—102.

Effects and its elimination method of envelope deformation on order analysis

CHENGWei-dong1,WANGTian-yang1,WANGJin-jiang2,RobertXGao2,WENWei-gang1,LIJian-yong1

(1.School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University,Beijing 100044, China; 2.Department of Mechanical Engineering, University of Connecticut, Storrs, CT 06269, USA)

Defects diagnosis of rolling element bearings operating under time-varying rotational speeds entails order tracking and analysis techniques that convert a vibration signal from the time domain to the angle domain to eliminate the effect of speed variations. Angular domain re-sampling will induce shock envelope deformation leading to errors of analysis, and the effect is particularly noteworthy when the varying rate of speed is significant. This paper presents a quantitative analysis of key factors affecting the accuracy of order analysis on rotating machines with varying speeds. An analytical model is established, simulated, and experimentally evaluated. Elimination methods are proposed for which the angle value should be modified by removing the peak interval variations. The research findings show that deformation of the envelope in the width direction has no effect on results of the order analysis; interval variations of adjacent envelope peaks have influence on the results of the order analysis; removing the peak interval variations in angle sequence can eliminate the effects of envelope deformation.

fault diagnosis; rolling bearing; computed order tracking; angular resampling; deformation of envelope

2014-02-09；

2014-05-06

国家自然科学基金资助项目(51275030); 中央高校基本业务专项资金资助项目(2011BM093)

TH165+.3; TP277

A

1004-4523(2015)03-0470-08

10.16385/j.cnki.issn.1004-4523.2015.03.018

程卫东(1967—),男，副教授。电话： (010)51683874；E-mail:wdcheng@bjtu.edu.cn