一类非耗散的显式时间积分方法

杨 超， 肖守讷， 阳光武， 朱 涛， 杨 冰

(西南交通大学牵引动力国家重点实验室，四川 成都 610031)

一类非耗散的显式时间积分方法

杨 超， 肖守讷， 阳光武， 朱 涛， 杨 冰

(西南交通大学牵引动力国家重点实验室，四川 成都 610031)

针对大型复杂结构的动力学问题，为了得到高效的计算方法，以泰勒公式为基础，通过调整参数改善算法的稳定性，得到了一类具有非耗散特性且以加速度为基本变量的显式数值积分方法。对提出的方法进行了稳定性和精度分析，并通过多个算例对提出的方法、蛙跳式中心差分法、Newmark-β法和精确解进行比较。结果表明，无阻尼情况下，所提出的方法的稳定性条件与中心差分法相同；提出的方法的振幅衰减率为0，具有非耗散特性，其周期误差约为隐式Newmark-β法的一半；所提出的方法给出了蛙跳式中心差分法和无耗散特性的翟方法的统一格式，并可以衍生出更多的显式时间积分方法。

显式方法； 非耗散； 差分格式； 精度； 稳定性

引 言

结构动力分析的数值解法可以分为模态叠加法和直接积分法，其中直接积分法按照求解方式还可以分为隐式法和显式法。隐式法有Newmark-β法[1]和Wilson-θ法[2]等，通常应用于低频响应占主导地位的长时间结构响应问题或准线性问题。显式法中最具代表性的是中心差分法[3]，通常应用于高频响应占主导地位的非线性问题或瞬态问题。对于大型非线性的动力学计算问题，显式方法的应用更加广泛。随着结构动力响应分析向复杂非线性的方向发展，计算量和计算代价显著提高，计算方法的速度和精度越来越受到重视。

文献[4]提出了一种具有三阶精度的显式差分方法，适用于有阻尼系统的动力响应分析，高阶精度需要增加中间变量而使整体计算量增加[5]。隐式算法也可以转换为显式算法，一般以位移为第一求解变量[6]。文献[7]提出了Newmark更新精细积分法，具有良好的稳定性，但要求阻尼矩阵为对角矩阵，所以只能属于半显式的方法。很多新开发的算法一般都是基于泰勒展开或加权残余法[8]，应用泰勒公式展开并截除高阶小量会引入一定的误差，而加权残余法也同样存在一定的误差，所以在考虑计算速度的同时要尽量提高算法精度。

现有的研究大多以位移为基本变量，速度和加速度通过对位移的求导获得，而以加速度为基本变量的方法很少受到重视。本文以加速度为基本变量，速度和位移通过对加速度的近似积分获得，在泰勒展开的基础上，通过调整积分参数改善算法的稳定性，提出了一类无耗散特性的显式时间积分方法。文中提出的方法的稳定性条件与中心差分法相同，其周期误差仅为Newmark-β法的一半。文中提出的显式时间积分方法统一了蛙跳式中心差分法和翟方法(φ=φ=0.5)，并可以衍生出更多的无耗散特性的显式积分格式。

1 显式方法

显式是指增量步结束时的状态仅依赖于该增量步开始之前的位移、速度和加速度，计算时不需要进行迭代或矩阵求逆。结构的动力学运动方程为

(1)

1.1 中心差分法

文献[9-10]中通常所描述的中心差分法(CDM)一般都是半显式格式的，在阻尼矩阵为非对角的情况下会退化为隐式格式。中心差分法对运动方程直接进行积分，其主要公式如下

(2)

将式(2)带入式(1)，得到以位移为第一求解变量的运动方程

(3)

中心差分法先利用式(3)求得tn+1时刻的位移，然后根据式(2)进行两次求导得到tn时刻的速度和加速度。这种半显式的中心差分法是以位移为基本变量，不存在算法阻尼，具有二阶精度。

1.2 蛙跳式中心差分法

蛙跳式中心差分法是中心差分法的一种变异形式，是完全显式格式的[9]。该方法的独特之处在于：取单个时间步中间时刻的点作为普通中心差分法的第三点，每个循环内只涉及单个时间步长内的物理量，中间时刻的点只计算速度，整数时刻的点只计算位移和加速度，这种跳跃步进方式犹如蛙跳一般。在增量步开始时，首先计算当前时刻的加速度为：

(4)

(5)

(6)

1.3 翟方法

翟方法[12]是由翟婉明院士提出的一类显式二步数值积分方法，该方法是基于著名的Newmark隐式积分方法构造的一类显式积分方法，所以两者的格式较为接近，其积分格式为

(7)

式中φ,φ为积分参数，一般取为0.5；在得到tn+1时刻的位移和速度后，就可以由式(8)得到该时刻的加速度。

(8)

翟方法具有二阶精度，在积分参数都为0.5时不存在算法阻尼，与Newmark-β法具有类似的算法阻尼特性。该显式方法也是以加速度为基本变量，只要其质量阵是对角阵或经对角化而不论阻尼阵如何复杂，积分过程中都无须联立求解耦合方程组，避免了组装等效刚度矩阵和矩阵求逆，这就大大节省了计算内存和时间，因而用于分析工程中大型非线性结构动力问题时，可以显著地提高计算速度和效率。

2 基于加速度的显式积分方法

蛙跳式中心差分法和翟方法具有共同的特征：以加速度为基本变量，无数值阻尼，即无耗散特性。根据这些特点，本文以泰勒展开公式为基础，通过研究可变参数对算法稳定性的影响，得到了一类非耗散的显式数值积分方法。首先用泰勒公式表示位移和速度

(9)

假设加速度的导数满足向后差分公式，则有

(10)

把式(10)带入式(9)，并略去高阶项，得到

(11)

将式(11)中值不为1的系数以变量代替

(12)

式(12)中，推荐取α=1,β=γ,γ∈[0,1]，γ的取值尽量接近0.5，此时该算法仅有唯一的可变参量γ，具有非耗散特性，即不存在算法阻尼，这个结果是通过下文的稳定性分析得到的。当3个系数变量取上述值时，结合式(8)，即为本文要提出的显式时间积分方法，其计算过程归纳如下：

1.计算起步

(1)形成质量矩阵M、刚度矩阵K和阻尼矩阵C；

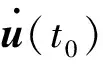
2.循环开始

(2)更新矩阵M，K和C；

3 稳定性与精度分析

多自由度系统中各类积分算法的稳定性和精度一般可以通过研究算法对单自由度系统的响应性质来实现。单自由度振动系统的动力学方程为

(13)

式中ζ，ω和fn分别为振动系统的阻尼比、自振圆频率和激励载荷。

3.1 稳定性分析

为了导出稳定性条件，由式(12)和式(13)，得到加速度显式法的递推公式为

(14)

式中A为积分逼近算子矩阵，令采样频率Ω=Δtω，得到

(15)

式中P=-2(1+γ)ζΩ-αΩ2,Q=2γζΩ+γΩ2。

由稳定性原理可知，λi为矩阵A的第i个特征值，当矩阵A的谱半径ρ(A)=max|λi|<1时，特征方程有共轭复根，积分格式是收敛的；当谱半径ρ(A)=1时，积分格式是临界稳定的[13]。通过求解特征方程的解析解发现，当阻尼比ζ=0时，加速度显式法的时间步长稳定区间与中心差分法是一样的，在(0,2/ω)之间。

如图1所示，在无阻尼情况下，α<1时，谱半径大于1，积分格式是发散的，不能符合要求；α>1时，谱半径存在小于1的区间，积分格式是收敛的，存在算法阻尼，即振幅会随着时间增长而不断衰减；当α=1且β≠γ时，积分格式存在起始点不为0的稳定区间，这意味着步长取某值时算法是稳定的，但进一步减小时间步长时算法可能不稳定；只有在α=1并且β=γ时，通过分析高次方程的解，无论γ取何值，谱半径在Ω∈(0,2)都是恒等于1的，振幅既不衰减也不发散而保持恒定，此时算法具有非耗散特性。图2显示了阻尼对加速度显式法的稳定性影响，随着阻尼比的增大，算法稳定区间逐渐减小。谱半径越小，表示算法收敛越快。

图1 无阻尼时加速度显式法的稳定性Fig.1 The stability of the acceleration explicit methods under undamped condition

图2 阻尼对稳定性的影响(γ=0.2)Fig.2 The influence of damping to the stability (γ=0.2)

3.2 精度分析

积分逼近算子矩阵具有一对共轭复根，可以用这对共轭复根表示出振动方程的解

(16)

(17)

振幅衰减率AD反映了幅值误差，周期延长率TD反映了周期误差，见式(18)和(19)，因此算法的精确度可以由振幅衰减率和周期延长率来度量。

(18)

(19)

在无阻尼情况下，将加速度显式法、Newmark-β法和中心差分法(CDM)的振幅衰减率和周期延长率进行比较。由图3可见，无耗散特性的加速度显式法、Newmark-β法和中心差分法的振幅衰减率都为0，说明幅值误差为0，而α=1.2时振幅会迅速衰减，这与稳定性结果是一致的。如图4所示，无阻尼情况下，隐式的Newmark-β法的周期是随着时间步长增加而逐渐变长的；无耗散特性的加速度显式法和中心差分法的周期延长率相同，周期都是缩小的，且周期误差约为Newmark-β法的一半。

图3 幅值误差Fig.3 The amplitude error

图4 周期误差Fig.4 The periodic error

4 算 例

采用文献[14]的算例，两自由度振动系统单端受恒定力激励，振动方程为

(20)

(21)

分别用文中提到的蛙跳式中心差分法(LCDM)、翟方法、Newmark-β法和本文方法(γ=0;γ=0.2;γ=0.5;γ=0.8)分别计算该振动系统，除了本文方法取了两种时间步长0.28和0.14 s，即最小周期的1/10和1/20，其他方法的时间步长都取0.14 s，质量点的加速度结果见图5和6，位移结果列于表1和2中。

图5 点1的加速度结果比较(Δt=0.14 s)Fig.5 The comparison of accelerations of point 1 (Δt=0.14 s)

图6 点2的加速度结果比较(Δt=0.14 s)Fig.6 The comparison of accelerations of point 2 (Δt=0.14 s)

表1 点1的位移结果比较

表2 点2的位移结果比较

本文方法(γ=0)和蛙跳式中心差分法的位移和加速度结果完全一致。γ<0.5时本文方法的结果相对于精确解有一定的相位延迟，误差较大。当γ=0.5时误差最小，Newmark-β法次之。所有方法中，本文方法(γ=0.5)的位移计算结果与精确解拟合度最高，其均方根误差也最小，其精度超过了隐式Newmark-β法。计算精度与计算速度通常是相互制约的两个指标，虽然蛙跳式中心差分法的误差偏大，但正因为其速度方面的优势才会被显式动力学软件采用，而通过循环公式可以看出本文方法与该方法在计算量上几乎相同，且精度可以通过积分参数调整。

从位移结果可以看出，本文方法的位移均方根误差随着时间步长增大而增大，本文方法对积分参数γ的选择是比较敏感的，随着γ从0增加到0.5，均方根误差逐渐减小，当γ从0.5逐渐增大时，均方根误差又开始增大，所以γ的推荐选取条件为：尽量接近0.5。

5 工程应用

5.1 铁路货车纵向振动

重载货物列车在货场通常要进行车辆之间的连挂，已连挂的车辆组受到被连挂车辆的冲击而产生振动。将车辆和钩缓装置组成的系统简化为由n个刚体串联组成的弹簧-质量系统[15]，车辆与钩缓装置的数目相等。为了分析方便，假设冲击端的车辆由简谐力激励，不受冲击最末端的钩缓装置一端被固定，钩缓装置考虑为渐进软化的非线性弹簧。

简化模型的参数为：车辆数为100，简谐力fn=106sin(18t) N，质量mi=50 000 kg，非线性弹簧刚度为ki=109[1-(ui-ui-1)2] N/m，i=1,2,…,n。该系统的最小和最大圆频率分别为2.21和282.81 rad/s，则本文方法的最大时间步长为0.007 s。为了便于比较，采用Newmark-β法步长Δt=0.000 5 s的结果作为“精确解”。根据上节中的算例确定的积分参数选取原则和时间步长Δt=0.007 s，约为最小周期的1/π，外载激励周期的1/50，最大周期的1/406，采用本文方法(γ=0.45)和Newmark-β法分别计算该模型。

采用硬件平台为戴尔Inspiron580微机，软件平台为64位MATLAB 2010a。受外力作用车辆的位移结果如图7所示。本文方法和Newmark-β法的计算结果与精确解在初始的半个最大周期基本重合，经过半个周期振动以后，振动趋势一致，幅值和相位与精确解相比存在误差，但本文方法的结果更接近精确解。当时间步长为0.007 s时，上述方法分别耗时0.484和1.967 s；当时间步长为0.000 5 s时，本文方法与Newmark-β法分别耗时6.582和27.04 s，相同条件下本文方法的速度约为Newmark-β法的4倍。此外，计算速度与程序语言的选取也是有关系的，若Newmark-β法取较大步长可以抵消计算速度上的弱势，但计算精度会降低。

图7 受力车辆的位移结果Fig.7 Displacement of the forced vehicle

5.2 铁路客车垂向振动

车辆振动试验台通过激励轮对使整节车厢振动，可以用于测试铁路客车的舒适度，而舒适度与车体加速度直接相关。为了模拟车辆振动试验台测试铁路客车垂向振动性能，根据达朗贝尔原理建立车辆的垂向动力学模型，模型简图和公式参见文献[12]和[16]。该模型为7刚体10自由度模型，包括1个车体、2个构架和4个轮对，车体和构架考虑沉浮自由度和点头自由度，轮对只考虑沉浮自由度。

车辆模型参数为：车体质量和点头惯量Mc=39 500 kg，Jc=2 312 000 kg·m2，构架质量和点头惯量为Mt=2 200 kg，Jt=2 200 kg·m2，轮对质量Mw=1 900 kg,一系悬挂刚度和阻尼为k1=2 130 000 N/m，c1=120 000 N·s/m，二系悬挂刚度和阻尼为k2=800 000 N/m，c2=217 400 N·s/m，车辆定距和转向架轴距为lc=18 m，lt=2.4 m。车辆的4个轮对采用正弦同相激励，假设激励力为ft=1 000sin(50t) N。该系统最小和最大圆频率分别为5.4和61.2 rad/s，由于阻尼的影响需要取时间步长为Δt=0.004 s，约为最小周期的1/25，外载激励周期的1/32，最大周期的1/290，分别采用文中提出的加速度显式法(AEM)和Newmark-β法计算该模型。以小步长的线性加速度法(LAM)的结果作为参考标准值，该小步长取Δt=0.000 4 s。

由于一系和二系阻尼的作用，车体响应逐渐趋于稳定，稳定后振动频率与激励频率一致。由于步长与激励周期的比值较小，所以计算结果之间差异很小，为了便于区别，图8中还给出车体稳定以后半个周期的车体垂向加速度时间历程。车体加速度在0.18 s以后趋于稳定，加速度显式法和Newmark-β法的结果的变化趋势与参考结果基本一致，但幅值上有差异，每个时间点对应的标准值位于加速度显式法和Newmark-β法的结果之间，加速度显式法的结果偏大，而Newmark-β法的结果偏小。

图8 车体加速度Fig.8 Acceleration of the carbody

6 结 论

本文提出了一类以加速度为基本变量的非耗散的显式时间积分方法，对加速度显式法进行了稳定性分析和精度分析，并通过一个线性算例和两个工程应用实例将加速度显式法和常用的经典方法进行了详细的比较，得到以下结论：

1) 加速度显式法是条件稳定的，与中心差分法具有相同的稳定区间；有阻尼情况下，加速度显式法的稳定区间随着阻尼的增大而减小。

2) 加速度显式法的振幅衰减率为0，具有非耗散特性；其周期延长率和中心差分法相同，周期误差约为隐式Newmark-β法的一半。算例表明加速度显式法在相同步长情况下具有较高的计算速度和精度。

3) 加速度显式法给出了蛙跳式中心差分法和无耗散特性的翟方法的统一格式，并可以衍生出更多的显式积分格式。

[1] Newmark N M. A method of computation for structural dynamics[J]. Journal of the Engineering Mechanics Division (ASCE), 1959, 85(3):67—94.

[2] Wilson E L, Farhoomand I, Bathe K J. Nonlinear dynamic analysis of complex structures[J]. Earthquake Engineering and Structural Dynamics, 1973，1(3): 241—252.

[3] 尚晓江, 苏建宇, 王化锋. ANSYS/LS-DYNA动力分析方法与工程实例[M]. 二版. 北京:中国水利水电出版社, 2008: 129—135.

[4] 张石磊,王焕定,张晓志. 结构地震响应分析新方法[J]. 国际地震动态, 2009，(6): 8—14.

Zhang Shilei, Wang Huanding, Zhang Xiaozhi. A new method in analyzing seismic response of the structure[J]. Recent Developments in World Seismology, 2009，(6): 8—14.

[5] Idesman A V, Schmidt M, Sierakowski R L. A new explicit predictor-multicorrector high-order accurate method for linear elastodynamics[J]. Journal of Sound and Vibration, 2008, 310(1/2): 217—229.

[6] Bonelli A, Bursi O S. Explicit predictor-multicorrector time discontinuous Galerkin methods for linear dynamics[J]. Journal of Sound and Vibration, 2001, 246(4):625—652.

[7] 郭泽英,李青宁. 动力反应分析的显式积分方法及其稳定性[J]. 地震工程与工程振动, 2008，28(2): 15—19.

Guo Zeying, Li Qingning. An explicit integral method and the stability of dynamic response analysis[J]. Journal of Earthquake Engineering and Engineering Vibration, 2008，28(2): 15—19.

[8] Stolle D. A direct integration algorithm and the consequence of numerical stability[J]. Journal of Sound and Vibration, 1995, 180(3): 513—518.

[9] 张雄, 王天舒. 计算动力学[M]. 北京:清华大学出版社, 2007: 140—207.

Zhang Xiong, Wang Tianshu. Computational Dynamics[M]. Beijing: Tsinghua University Press, 2007: 140—207.

[10]Wiberg N E, Li X D. Adaptive finite element procedures for linear and non-linear dynamics[J]. International Journal for Numerical Methods in Engineering, 1999, 46(10): 1 781—1 802.

[11]Hallquist J O. LS-DYNA Theory Manual[M]. Livermore Software Technology Corporation, 2006.

[12]翟婉明. 车辆-轨道耦合动力学[M]. 第2版. 北京:中国铁道出版社, 2002: 107—127.

Zhai Wanming. Vehicle-Track Coupling Dynamics[M]. 2nd ed. Beijing: China Railway Publishing House, 2002: 107—127.

[13]Hilbert H M. Collocation, dissipation and ‘Overshoot’ for time integration schemes in structural dynamics[J]. EESD, 1978, 6(1): 116—124.

[14]李常青,楼梦麟,余志武,等. 近似平衡多项式加速度动力显式算法[J]. 应用力学学报, 2011，28(5): 475—479.

Li Changqing, Lou Menglin, Yu Zhiwu, et al. Psedo-balance polynomial acceleration explicit method[J]. Chinese Journal of Applied Mechanics, 2011，28(5): 475—479.

[15]Chang S Y. Improved explicit method for structural dynamics[J]. Journal of Engineering Mechanics (ASCE), 2007,133(7):748—760.

[16]张志超,赵岩,林家浩. 车桥耦合系统非平稳随机振动分析[J]. 振动工程学报, 2007, 20(5): 339—446.

Zhang Zhichao, Zhao Yan, Li Jiahao. Non-stationary random vibration analysis for vehicle-bridge coupled systems[J]. Journal of Vibration Engineering, 2007, 20(5): 339—446.

Non-dissipative explicit time integration methods of the same class

YANGChao,XIAOShou-ne,YANGGuang-wu,ZHUTao,YANGBing

(Traction Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, China)

In order to obtain efficient calculation methods for dynamical problems of large and complex structures. A class of non-dissipitive explicit numerical integration methods is proposed through adjusting parameters to improve the stability of algorithms. Accelerations are used as the basic variables in the proposed methods which are on the basis of the Taylor's formula. The analyses of stability and accuracy are performed for the proposed methods. Finally, some numerical examples are given for the comparison between the proposed methods,and some current methods including the leapfrog central difference method (LCDM), the Newmark-βmethod and the exact solution. The results show that the proposed methods have the same stability condition as the LCDM under undamped condition. The amplitude attenuation of the proposed methods is 0, which means they are non-dissipative. The periodic error is about half of that of the implicit Newmark-βmethod. The proposed methods provide a unified format of the LCDM and the Zhai method without dissipation, and more explicit integration algorithms can be derived directly.

explicit method; non-dissipative; difference scheme; accuracy; stability

2014-01-05；

2014-07-16

国家自然科学基金资助项目(51275432，51405402)；铁道部科技研究开发计划资助项目(2011J022-A)；四川省科技厅应用基础研究项目(2014JY0242)

O241.8； O313

A

1004-4523(2015)03-0441-08

10.16385/j.cnki.issn.1004-4523.2015.03.014

杨超(1988—)，男，博士研究生。电话：15882317785 ； E-mail： yangchaosky@foxmail.com