一种基于子结构界面动刚度的模态综合法

诸 赟， 张美艳， 唐国安

(复旦大学力学与工程科学系， 上海 200433)

一种基于子结构界面动刚度的模态综合法

诸 赟， 张美艳， 唐国安

(复旦大学力学与工程科学系， 上海 200433)

针对传统模态综合法中由于高阶截断模态带来的计算误差问题，将子结构界面动刚度展开成频率的泰勒级数,表示为子结构的固定界面主模态。利用位移协调和力平衡条件对子结构界面动刚度进行模态综合，保留了截断模态高阶项的部分贡献，发展了一种新的模态综合方法。推导过程不必引入质量矩阵为对角块的假设，比现有改进方法更具普适性。数值算例的结果表明在相同自由度的前提下，该方法能获得更高的模态综合精度。

动态子结构； 模态综合法;动刚度

引 言

对于复杂结构，出于分工协作或工程实际的需要，将整体结构划分成若干个子结构分别进行动力学特性分析，然后根据子结构间界面的位移协调条件和力平衡条件进行综合，从而得到整体结构的动力学特性，这种由子结构动力学特性综合分析而得到整体结构动力学特性的方法就是动态子结构方法[1]。按照子结构界面自由度处理方法的不同，可以将动态子结构方法分为固定界面模态综合法、自由界面模态综合法和混合界面模态综合法[2]。其中，固定界面模态综合法在用子结构低阶模态信息表示高阶模态信息时不存在因刚体模态导致的奇异刚度矩阵的求逆问题，计算过程简单，得到了较多应用。

在固定界面模态综合法的工程应用中，Craig-Bampton-Hurty(CBH)方法[3-4]在计算低阶模态时具有精度高、易于编程等优点，包含在很多商业动力学计算软件中，解决了大量的复杂工程问题[5]。近十年间，许多学者对于CBH方法的工程应用做了深入的研究。邓峰岩等[6]探讨了CBH方法在多体动力学建模中的应用。黄道琼等应用CBH方法分析了四机并联发动机的低频特性[7]。史纪鑫等利用CBH方法对含复合柔性太阳翼的航天器进行了动力学建模[8]。孙晓阳等[9]利用CBH方法实现轮胎子结构模型与车辆多体动力学模型的耦合分析。高星斗等[10]利用CBH方法建立了车载导弹发射系统多体动力学模型。邓四二等[11]采用了CBH方法建立了高速角接触球轴承保持架柔体动力学方程。陈海卫等[12]采用CBH方法建立了波轮式洗衣机的刚柔耦合动力学模型。何鑫等[13]利用CBH方法建立了直升机起落架实验系统的刚柔耦合动力学模型。

在以上工程应用的研究中，CBH方法在计算低阶模态时表现出很高的精度，但该方法完全忽略高阶截断模态的影响，对于高阶模态的计算误差较大。Suarez和Singh[14]考虑了截断的高阶模态的影响，但是没有注意到新方法存在Ritz基线性相关的问题。邱吉宝和Williams[15]利用矩阵级数展开构造了非线性的特征方程，虽然充分考虑了高阶模态的影响，但是非线性的特征方程求解比较复杂，需要经过多次迭代。王缅和郑钢铁[16]提出的改进的固定界面模态综合法充分考虑了高阶截断模态的影响，且不会出现Ritz基线性相关问题和非线性的特征方程，但是该方法对结构的质量矩阵做了对角块的假设，限制了方法的应用范围。

为此，本文作者推导了子结构界面动刚度的完备级数展开式，在此基础上提出了基于位移协调和力平衡条件的模态综合方法。该方法保留了截断模态高阶项的贡献得以提高模态综合的精度，界面力高阶平衡条件的利用则减少了界面自由度的引入。在相同自由度的前提下，该方法能获得更高的模态综合精度，同时方法的推导过程不必引入质量矩阵为对角块的假设，比现有方法更具普适性。数值算例的计算结果表明了方法的有效性。

1 子结构界面动刚度表达式

考虑一子结构，内部和界面的位移分别记为Xi和Xj，相应的质量、刚度矩阵为

(1)

该子结构仅在界面力作用下的频域方程为

(2)

在固定界面条件下(Xj=0j)，内部位移满足运动方程

(3)

该特征方程具有ni=dim(xi)对固有频率和固有模态，记为

(4)

从固有频率和固有模态所满足的正交归一条件

(5)

可以导出

(6)

由式(6)得

(7)

对上式两端分别求逆后，得到固定界面条件下内部自由度的动柔度矩阵

(8)

其中

(9)

由方程(2)第一行，将内部位移Xi用界面位移Xj表示

(10)

则方程(2)中，第二行可以整理为界面力和界面位移的频域关系

(11)

(12)

利用式(8)，可以将界面动刚度用固定界面主模态表示为

(13)

由Δii(ω2)定义式可以推得

(14)

移项后可得

(15)

从而

(16)

将关系式(15)和(16)代入式(13)，经过整理得

(17)

将固定界面的固有频率和模态矩阵按低频和高频分块成

(18)

式中Ωkk和Φik是低阶固有频率和模态矩阵，Ωhh和Φih是高阶固有频率和模态矩阵，分别为

(19)

在此分块表示下，可推导出如下关系

(20)

利用上式和模态正交关系，方程(17)可以改写为

(21)

2 子结构界面动刚度的完备展开式

(22)

代入到式(21)，考虑到固有频率和模态矩阵满足关系

界面动刚度可以表示为

(23)

上式中

(24)

由方程(23)可知，子结构界面力和位移的关系为

(25)

引入辅助变量

(26)

则界面力与位移的关系式可以改写为

(27)

而辅助变量与界面位移的关系式可以写成约束方程形式

(28)

3 利用界面动刚度完备展开式的子结构综合

为便于表述，考虑一个含有两个子结构的系统，分别用下标“1”和“2”表示。由关系式(27)，界面力与界面位移的关系分别写成

(29)

引入位移协调和力平衡条件

(30)

可以得到两个子结构综合以后的频域平衡方程

(31)

上式中

(32)

两个子结构综合后的约束方程(28)变为

(33)

将方程(31)和(33)联立，得

(34)

4 界面位移高阶导数的消去

由约束方程(33)，可以将方程改写为

(35)

利用数学归纳法可以证明，在方程(35)两端同乘以ω2q(q≥1)，可以得到

(36)

在方程组(36)中取q=1,…,nT，并且略去ω2p(p>nT)项，经排列后得到

(37)

上式中

α=

由此可得

(38)

(39)

其中

(40)

(41)

上式中

将关系式(38)扩展成

(42)

代入方程(41)，并左乘矩阵TT，最终得到

(43)

其中

(44)

从方程(43)可以解出特征值和对应的特征向量

(45)

将这些特征向量写成分块形式

(46)

(47)

数值计算中，采用高次幂级数容易带来计算稳定性问题，在本文中具体表现为方程中系数矩阵α的条件数会变大。因此，级数阶次不宜过高，算例表明保留两项较为合适,即取nT=3。

5 数值算例

采用文献[14]中给出的直升机尾部桁架作为分析对象，结构如图1～3所示。整个结构左端固定，全部元件采用铝管组装，共计58个节点，192个单元。铝管的弹性模量E=7.239 5×1010Pa, 截面积A=8.193 5×10-4m2。惯性矩I=2.780 4×10-7m4，极惯矩J=4.646 8×10-7m4。整个结构分为a,b两个子结构，尾桁子结构的有限元模型，如图4,5所示。

图1 尾桁-顶视图Fig.1 Top-view of the tailboom

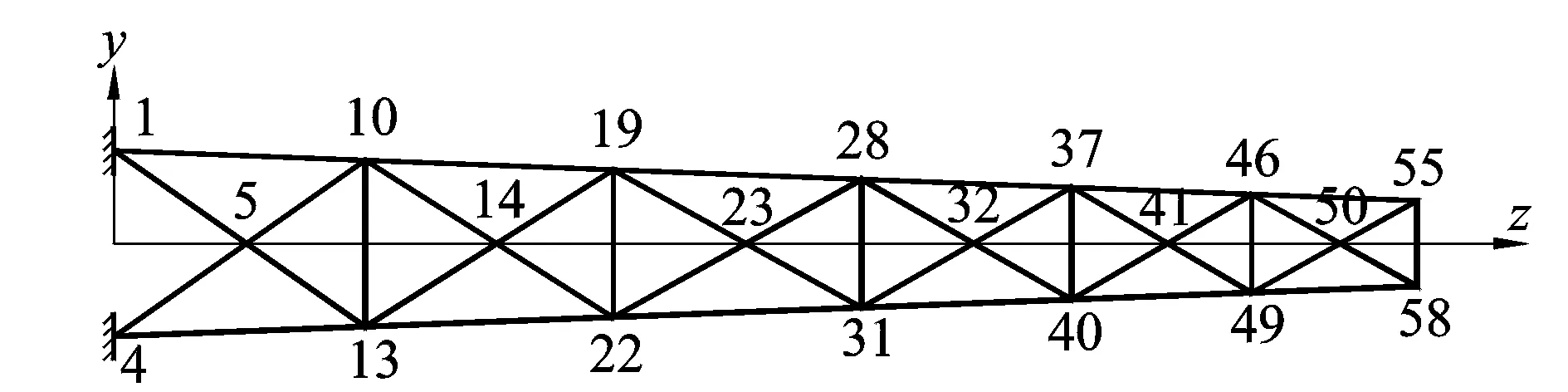
图2 尾桁-正视图Fig.2 Front-view of the tailboom

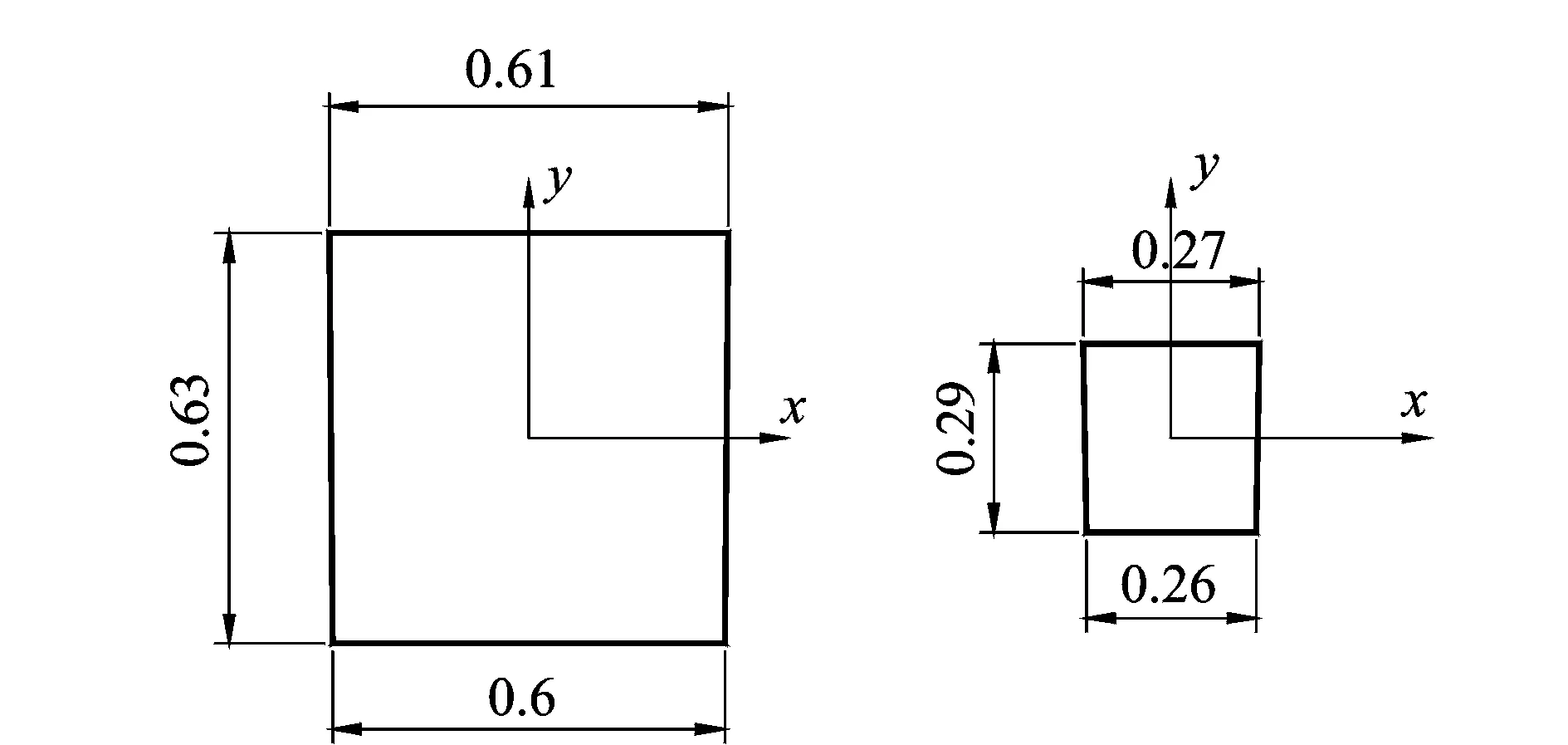
图3 直升机尾桁-端部图(单位:m)Fig.3 Base of the tailboom(Unit:m)

图4 子结构a的有限元模型Fig.4 Finite element model of substructure a

图5 子结构b的有限元模型Fig.5 Finite element model of substructure b

子结构a端部固定后的自由度为138，子结构b的自由度数目为162。两个子结构的界面共有4个节点、24个自由度，节点编号为28#,29#,30#,31#。

整体结构200 Hz以下的固有频率计算结果如表1。表中还列出了整体有限元模型计算结果以及CBH方法的计算结果，其中误差err定义为

如表1所示，在100 Hz以下及附近，本文方法与CBH方法精度都非常高，与有限元方法相比的误差均不超过1%，在200 Hz附近，本文方法的精度明显高于CBH方法。

表1 固有频率计算结果

表2 子结构一致质量矩阵结果与对角块质量阵结果比较

Tab.2 Results comparison between substructure consistent mass matrix and diagonal dominance mass matrix

阶次Mij=0时的固有频率Mij≠0时的固有频率相对误差121．29920．96941．57%222．47422．12441．58%3103．610399．67663．95%4107．5918104．12053．33%5109．3923105．30313．88%6192．3118188．35962．10%

表2结果表明，文献[16]将子结构质量矩阵设为对角块矩阵的假设，会带来高达3.95%的模型误差，相比表1中1%以内的计算误差要大得多。可见文献[16]关于质量矩阵是对角块的假设有一定的局限性。在有限元建模时，即便采用集中质量矩阵，当体系中存在多点约束关系时，质量矩阵仍然会表现出非对角块形式，多点约束关系是复杂结构建模常用的手段。本文方法是对文献[16]的完善，取消了质量矩阵对角块的假设，同时保留了对宽频动力学分析的优势[17]。

图6 调整后尾桁-端部图(单位:m)Fig.6 base of the tailboom with repeated frequency(Unit:m)

为了考察本文方法在结构(子结构)具有重频情况下的适用性, 将直升机尾部桁架截面调整为正方形，两端截面如图6所示，材料参数和其他几何尺寸保持不变。此时，直升机尾桁整体结构和两个子结构均有重频。同样分析直升机尾桁整体结构200 Hz以下的固有频率, 取ca=2，子结构的截断频率为400Hz,子结构a和b的保留模态个数分别为15和5。利用本文方法分析得到的结果、CBH方法的计算结果与整体有限元模型计算结果比较如表3所示。表3结果与表1结果类似，本文方法的精度明显高于CBH方法。说明本文的研究方法可以直接应用到结构存在密频和重频的情形。

表3 重频结构固有频率计算结果

Tab.3 Results of the natural frequency for structure with repeated frequency

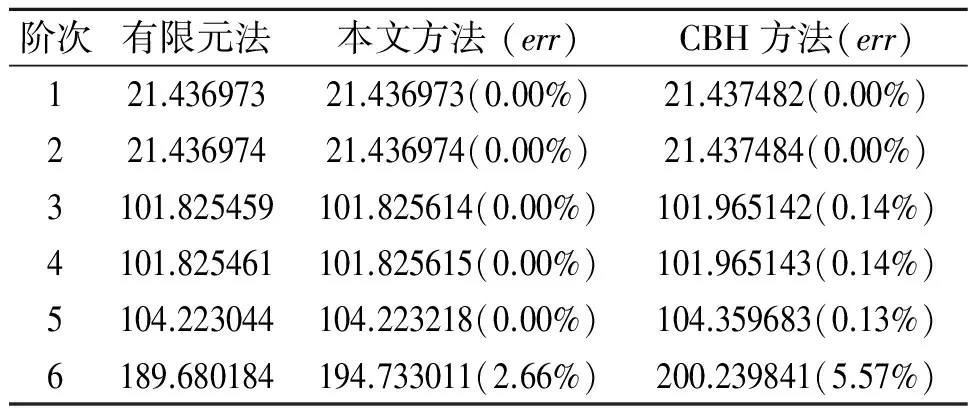
阶次有限元法本文方法(err)CBH方法(err)121．43697321．436973(0．00%)21．437482(0．00%)221．43697421．436974(0．00%)21．437484(0．00%)3101．825459101．825614(0．00%)101．965142(0．14%)4101．825461101．825615(0．00%)101．965143(0．14%)5104．223044104．223218(0．00%)104．359683(0．13%)6189．680184194．733011(2．66%)200．239841(5．57%)

6 结 论

作者吸收了国内外学者对固定界面模态综合法所做的改进工作，从推导子结构界面动刚度的完备级数展开式出发，提出了基于位移协调和界面力高阶平衡条件的动态子结构综合方法，获得了更高的模态综合精度，同时克服了现有改进方法中对质量矩阵所作的对角块假设。数值算例的计算结果说明了本文方法是行之有效的。

本文方法引入了界面自由度的高阶导数，通过高阶的力平衡条件消去了这些变量，经模态综合得到的模型自由度与CBH方法相同。模态综合过程中，最大的计算量在于求解固定界面条件下的子结构固有频率和模态，与CBH方法相比并没有明显增加。因此，该方法具有较高的计算效率。

[1] 叶淑琴. 基于中阶模态的固定界面子结构精确综合[D]. 杭州：浙江大学，2010.

Ye Shu-qin. Exact Fixed-Interfacial Substructure Synthesis Using Medium-Order Normal Modes[D]. Hangzhou：Zhejiang University，2010.

[2] 邱吉宝，向树红，张正平. 计算结构动力学[M]. 合肥:中国科学技术大学出版社，2009：346—351.

Qiu Ji-bao，Xiang Shu-hong，Zhang Zhen-ping. Computational Structural Dynamics [M]. Hefei：Press of University of Science and Technology of China，2009：346—351.

[3] Hurty W C. Dynamic analysis of structural systems using component modes [J]. AIAA Journal，1965，3(4): 678—685.

[4] Bampton M C C，Craig Jr R R. Coupling of substructures for dynamic analyses [J]. AIAA Journal，1968，6(7):1 313—1 319.

[5] 李英强. 基于模态综合的汽车结构优化研究[D]. 重庆：重庆大学, 2012.

Li Ying-qiang. Study on Automotive Structural Optimization based on Component Mode Synthesis[D]. Chongqing：Chongqing University,2012.

[6] 邓峰岩, 和兴锁, 张娟，等. 修正的Craig-Bampton方法在多体系统动力学建模中的应用[J]. 机械设计，2004，21(3): 41—43.

Deng Feng-yan，He Xing-suo，Zhang Juan，et al. Application of a modified Craig-Bampton method in dynamics modeling of multi-body system [J]. Journal of Machine Design，2004，21(3): 41—43.

[7] 黄道琼, 张继桐, 何洪庆. 四机并联发动机低频动态特性分析[J]. 火箭推进, 2004, 30(4): 27—31.

Huang Dao-qiong，Zhang Ji-tong，He Hong-qing. Low frequency dynamic characteristics of four parallel connected engines [J]. Journal of Rocket Propulsion，2004，30(4): 27—31.

[8] 史纪鑫, 曲广吉. 可变构型复台柔性结构航天器动力学建模研究[J]. 宇航学报, 2007, 28(1): 130—135.

Shi Ji-xin，Qu Guang-ji. Methematical modeling of a class of variable structure spacecraft with flexible multibody appendages [J]. Journal of Astronautics，2007，28(1): 130—135.

[9] 张晓阳, 孙蓓蓓, 陈南. 基于修正Craig-Bampton方法的轮胎动态子结构模型[J]. 农业机械学报, 2009, 40(9): 41—45.

Zhang Xiao-yang，Sun Bei-bei，Chen Nan，et al. Dynamic Substructure Tire Model Based on Modified Craig-Bampton Method [J]. Transactions of the Chinese Society for Agricultural Machinery，2009，28(1): 41—45.

[10]高星斗, 毕世华, 陈阵. 基于改进Craig-Bampton法的导弹发射过程多柔体动力学研究[J]. 固体火箭技术, 2011, 34(5): 559—563.

Gao Xing-dou，Bi Shi-hua，Chen Zhen. Flexible multi-body dynamics analysis during missile launching based on improved Craig-Bampton method [J]. Journal of Solid Rocket Technology，2011，34(5): 559—563.

[11]邓四二, 谢鹏飞, 杨海生，等. 高速角接触球轴承保持架柔体动力学分析[J]. 兵工学报, 2011,32(5): 625—631.

Deng Si-er，Xie Peng-fei，Yang Hai-sheng，et al. Dynamic analysis of flexible cage of high-speed angular contact ball bearing [J]. Journal of China Ordnance，2011，32(5): 625—631.

[12]陈海卫, 张秋菊, 曹毅. 波轮式全自动洗衣机刚柔耦合模型的建立[J]. 振动与冲击, 2012, 31(15): 185—189.

Chen Hai-wei，Zhang Qiu-ju，Cao Yi. Flexible model for a vertical axis automatic washing machine [J]. Journal of Vibration and Shock，2012，31(15): 185—189.

[13]何鑫, 许锋, 聂宏. 直升机起落架虚拟静力试验方法研究[J]. 航空计算技术, 2013, 43(2): 33—36.

He Xin，Xu Feng，Nie Hong. Research of virtual static test of helicopter landing gear [J]. Aeronautical Computing Technique，2013，43(2): 33—36.

[14]Suarez L E，Singh M P. Improved fixed interface method for modal synthesis [J]. AIAA Journal，1992，30(12): 2 952—2 958.

[15]Qiu Ying，Williams F W. Exact modal synthesis techniques using residual constraint modes [J]. International Journal for Numerical Methods in Engineering，1997，40(13): 2 475—2 492.

[16]王缅，郑钢铁. 一种改进的固定界面模态综合法[J].宇航学报，2012，33(1): 291—297.

Wang Mian，Zheng Gang-tie. An improved fixed-interface modal synthesis method[J]. Journal of Astronautics，2012，33(1): 291—297.

[17]王缅.有限元动力学宽频带计算与连接结构实验建模方法研究[D].北京：清华大学，2011.

A modal synthesis method based upon dynamic stiffness on interface

ZHUYun,ZHANGMei-yan,TANGGuo-an

(Department of Mechanics and Engineering Science , Fudan University , Shanghai 200433 , China)

A new modal synthesis method is proposed in this paper for reducing errors caused by higher order modal truncations. Through series expansion, the dynamic stiffness on substructure interface is represented by the normal mode of the fixed-interface substructure. In addition, geometrical compatibility and force equilibrium on substructure interface are employed in the modal synthesis of the dynamic stiffness. Thus, a new methodology of substructure synthesis is obtained. The higher order force equilibrium on the substructure interface is employed to achieve the model reduction. Compared to Craig-Bampton method, this method keeps the contribution of the higher order terms of the truncated modes so that it can improve the accuracy of the modal synthesis. The deduction doesn′t introduce the assumption of the diagonal mass matrix which makes the method more general. The numerical result is given to show the effectiveness of the method.

dynamic substructure; mode synthesis; dynamic stiffness

2013-12-30；

2014-06-30

国家自然科学基金资助项目(11202052)

O326;V214.1

A

1004-4523(2015)03-0345-07

10.16385/j.cnki.issn.1004-4523.2015.03.002

诸赟(1984—)，男，博士研究生。电话：(021)58598280;E-mail: 072029014@fudan.edu.cn

唐国安(1952—)，男，教授。E-mail: tangguoan@fudan.edu.cn