嫦娥三号软着陆轨道设计与控制策略
杨永辉,刘 睿,李 华
(1.西北核技术研究所,陕西 西安 710024;2.西安航空学院 理学院,陕西 西安 710077)
嫦娥三号软着陆轨道设计与控制策略
杨永辉1,刘 睿2,李 华2
(1.西北核技术研究所,陕西 西安 710024;2.西安航空学院 理学院,陕西 西安 710077)
针对嫦娥三号软着陆的轨道设计和控制策略进行研究。首先,采用开普勒第一、二定律求出嫦娥三号在近月点与远月点的相对速度与着陆点的相对位置。其次,将嫦娥三号软着陆过程分为六个阶段,利用动力学微分方程,针对每个阶段,建立消耗燃料最少为目标的优化模型。由开关控制理论与极小值原理,得到六个阶段的点火时间和推力。最后,通过稳定性分析,可知本文所设计的控制策略轨道具备误差小、敏感性低的优点。
开关控制;平滑度矩阵;搜索算法
0 引言
开发月球资源,建立月球基地已成为世界航天活动的必然趋势与竞争热点。我国已迈出航天深空探测第一步,开展月球探测工作。而在月球表面实现软着陆则是月球勘探的重要前提。嫦娥三号于2013年12月2日1时30分成功发射,12月6日抵达月球轨道。嫦娥三号在着陆准备轨道上的运行质量为2.4t,其安装在下部的主减速发动机能够产生1500N到7500N的可调节推力,其比冲(即单位质量的推进剂产生的推力)为2940m/s,可以满足调整速度的控制要求。在四周安装有姿态调整发动机,在给定主减速发动机的推力方向后,能够自动通过多个发动机的脉冲组合实现各种姿态的调整控制。嫦娥三号的预定着陆点为19.51W,44.12N,海拔为-2641m。嫦娥三号已于北京时间12月14号在月球表面实施软着陆,其如何实现软着陆已成为全世界关注的焦点。
Apollo系列则是通过宇航员观测着陆区并操纵人控系统实现了避障和安全着陆。凤凰号探测器成功实现了火星软着陆,其采用了事先筛选高概率安全着陆区来避免大障碍的危害[1]。NEAR探测器首次实现了小行星着陆任务,但由于姿控误差较大等原因,探测器未能实现避障就继续向小行星表面下降了[2-8]。
嫦娥三号的核心任务是实施高可靠高安全的月面软着陆,要求着陆器必需具备自主障碍识别与规避能力。本文针对嫦娥三号软着陆的轨道设计和控制策略进行研究。
首先,采用开普勒第一、二定律求出嫦娥三号在近月点与远月点的相对速度与着陆点的相对位置。
其次,将嫦娥三号软着陆过程分为六个阶段,利用动力学微分方程,分别针对每个阶段,建立消耗燃料最少为目标的优化模型。由开关控制的理论与极小值原理,得到六个阶段的点火时间和推力。
最后,通过稳定性分析,可知本文所设计的控制策略轨道具备误差小、敏感性低的优点。
1 嫦娥三号软着陆过程的六个阶段
嫦娥三号软着陆过程分为六个阶段,如图1所示。

图1 嫦娥三号软着陆过程示意图
2 嫦娥三号在近月点与远月点的相对速度与着陆点的相对位置
为了确定着陆准备轨道中近月点和远月点的相对速度与相对位置,本文将其转化为求解主减速阶段与快速调整阶段中探月器产生水平位移之和的问题。
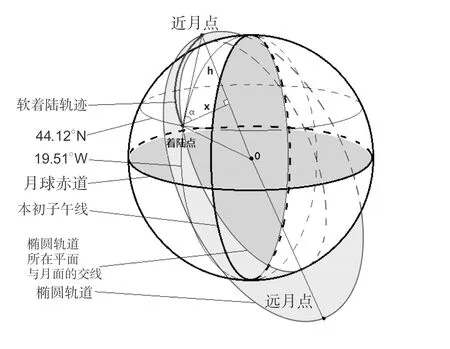
图2 近月点与远月点示意图
2.1 嫦娥三号在近月点和远月点的速度
由开普勒第一定律知,嫦娥三号围绕月球的运动轨道为椭圆轨道,在由近月点A到远月点B的过程中,根据机械能守恒定律得:
(1)
由开普勒第二定律得到:
(2)
其中,m为嫦娥三号的质量,M为月球质量,RA为近月点到月心的距离,RB为远月点到月心的距离,vA为嫦娥三号在近月点的速度,vB为嫦娥三号在远月点的速度。由式(2)可得:
vA=1.69km/s,方向沿椭圆轨道的切线方向指向着陆点;vB=1.14km/s,方向与近月点速度方向相反。
2.2 近月点及远月点的位置
嫦娥三号在近月点、远月点的位置取决于主减速阶段、调整阶段的嫦娥三号水平位移。
2.2.1 嫦娥三号在主减速阶段水平位移
对嫦娥三号在主减速阶段降落的分析得图3:
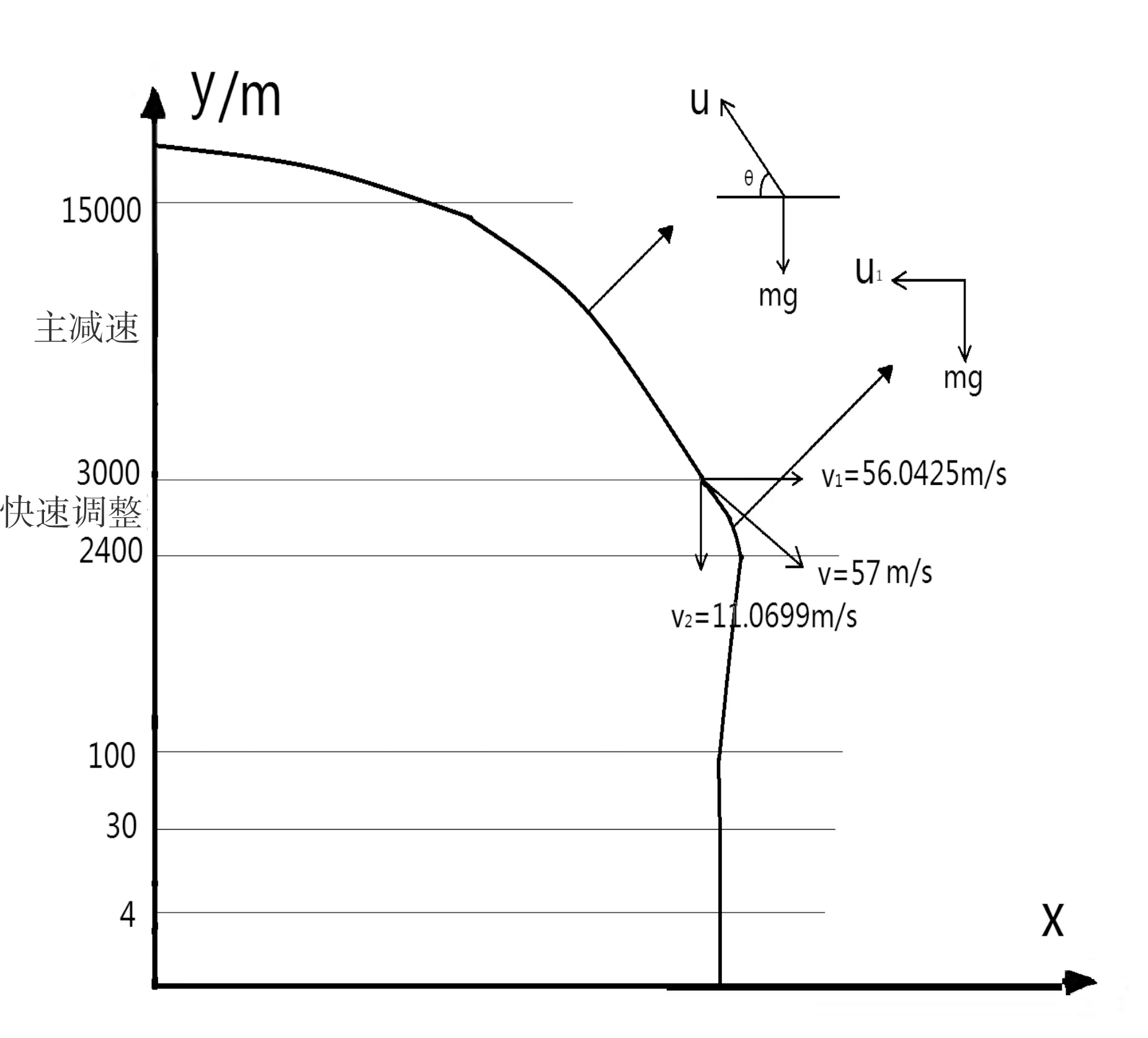
图3 主减速阶段示意图
此阶段嫦娥三号距月球表面的海拔变化为15000m~3000m。t为嫦娥三号从近月点到距月球表面某一高度的时间间隔,u为嫦娥三号发动机的推力,v为嫦娥三号的瞬时飞行速度,g为月球表面的重力加速度,v0为嫦娥三号在近月点的速度,即:v0=vA,v1为嫦娥三号到达距离月球表面3000m时的水平速度,v2为嫦娥三号到达距离月球表面3000m时竖直速度,v12为嫦娥三号到达距离月球表面3000m的速度,ve是以米/秒为单位的比冲,x1为此阶段嫦娥三号的水平位移。则:
(3)
利用Matlab可求得非线性方程的解为:
v1=56.0425m/s,v2=11.0699m/s,t1= 137.2116s,x1=214667.5m
2.2.2 嫦娥三号在快速调整阶段降落过程中的水平位移
此阶段嫦娥三号距月球表面的海拔变化为3000m~2400m。假设此阶段的推力不变,且嫦娥三号到距月球表面2400m时,水平速度为零。为保证降落过程中燃料消耗最少,此阶段的推力方向平行于月球表面。
设u1为此阶段发动机的推力,x2为此阶段嫦娥三号的水平位移。则
(4)
利用Matlab中的牛顿迭代法求非线性方程的解:
t2=30.6822m/s,u1=4055.8N,x2=859.8m
近月点到着陆点之间的水平距离为:x=x1+x2=215530m
由3.2.1与3.2.2可知,近月点距着陆点的水平距离为215.5km,竖直方向距离15km。远月点距着陆点的水平距离为215.5km,竖直方向距离100km。
3 嫦娥三号软着陆轨道设计与控制策略
根据图1所示的六个阶段,逐段进行软着陆轨道与控制策略的设计。
3.1 主减速阶段
主减速阶段的状态方程如下:
(5)

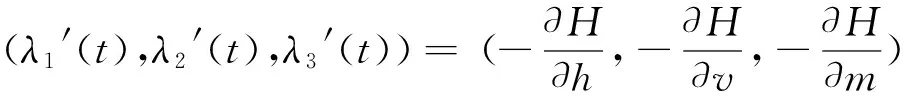
(6)
终端的横截条件为:
(λ1(tf),λ2(tf),λ3(tf))=(γ1,γ2,-1)
(7)
得最优控制u*(t)为:

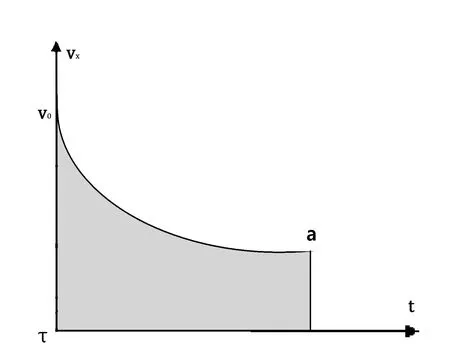
图4 水平速度分量的v-t图像

图5 竖直速度分量的v-t图像

(8)
其中M′为嫦娥三号无燃料时的质量。
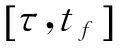
m(t)=-ka(t-τ)+m(τ)
(9)
为了直观形象地研究探月器的运动,在相平面(v(t),h(t))上继续讨论探月器的运动轨迹。
在主减速阶段的后半段,u*(t)=a,且当t=tf时h(tf)=3000,v(tf)=57,tf-τ=td,代入式(9)中得到
(10)
(11)
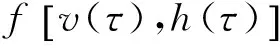
在主减速阶段前半段u=0,由(9)得
两条运动轨迹作图如下:

图6 运动轨迹
两条运动轨迹的交点为最优控制的切换点,由图6可以看出交点的横坐标无限接近于坐标原点,可认为从探月器进入主减速阶段的时刻开始,开关函数控制主发动机提供最大推力。
主减速阶段嫦娥三号从近月点开始点火,主发动机以最大推力来提供减速动力,主减速阶段结束时,水平速度v1=56.0425m/s,竖直速度v2=11.0699m/s,历时t1= 137.2116s,嫦娥三号的质量:m1=2262.8kg。
3.2 快速调整阶段
此阶段嫦娥三号距月球表面的海拔变化为3000m~2400m。根据主减速阶段的最优控制策略,我们将探月器在快速调整阶段主发动机提供的减速动力也进行开关控制,使发动机在切换时刻τ之前提供恒定的水平最大推力,使之水平速度减小到零,而在切换时刻τ之后不提供推力,以此来减小燃料消耗。
以月球表面3000米的时刻为零时刻,建立动力学方程:
求解得到:x3=464.93m,t3=16.6s,h1=358.23m

3.3 粗避障阶段
此阶段嫦娥三号距月球表面的海拔变化为2400m~100m。分为两个部分,一个部分是控制启动主发动机控制竖直推力的时刻,使燃料消耗最少;另一部分是启动姿态调整发动机控制水平推力,使探月器粗步避开大陨石坑。
3.3.1 控制竖直推力
根据最优控制策略,减小燃料消耗,将探月器在粗避障阶段主发动机提供的减速动力也进行开关控制,使发动机在切换时刻τ之前不提供推力,而在切换时刻τ之后,提供恒定的竖直向上的最大推力。
根据上述减速动力控制原则,嫦娥三号在竖直方向上先进行自由落体运动,再进行加速度不断变大的减速运动。当到达距月球表面100m时竖直方向上的速度减小到零,并保持悬停。
设t5表示自由落体的时间,制动时间为t6,h2表示自由落体过程中下降的高度。
由Matlab解得:t5=30.78s,h2=2041m,t6=16.76s。到达距月球表面距离为100米时,嫦娥三号的质量m3=2169.1kg。
3.3.2 控制水平推力
将2400m处高程图(图7)导入到2300×2300的矩阵A中,
并计算矩阵中各点的平滑度η:
得到平滑度矩阵
以2400米处高程图的图像中心点为中心辐射,搜索平滑度矩阵中4×4范围内平滑度之和小于筛选精度μ1的点,令μ1=0.5,求得图像中心左上方点的位置坐标。
以此类推,找到图像全部范围内符合筛选精度的点,从而找到距离图像中心点最近的点作为粗避障的目标点,坐标为(1150,1145),距预定着陆点的水平距离为5m。

图7 2400m处高程图
3.3 精避障阶段
将100m处的高程图的图像(图8)导入到1000×1000的矩阵B中,
计算矩阵中各点的平滑度η(同粗避障阶段),得到平滑度矩阵,以图像中心点辐射,搜索平滑度矩阵中10×10范围内平滑度之和小于筛选精度μ的点,此时我们设定μ=10,求得图像中心左上方所有点的位置坐标。

图8 100m处高程图
以此类推,找到图像全部范围内符合筛选精度的点,从而找到距离图像中心点最近的点作为精避障的目标点,即最终的实际着陆点,坐标为(445,500),距预定着陆点的垂直距离为5.5m。
3.4 缓速下降阶段
此阶段嫦娥三号距月球表面的海拔变化为100m~4m,根据燃料消耗最小原则,将探月器在上述两个阶段主发动机提供的减速动力进行开关控制,使发动机在切换时刻τ之前不提供推力,而在切换时刻τ之后,提供恒定的竖直向上的最大推力。
根据上述减速动力控制原则,嫦娥三号在竖直方向上先进行自由落体运动,再进行加速度不断变大的减速运动。当到达距月球表面100m时竖直方向上的速度减小到零,并保持悬停。
此过程中的自由落体的时间t7=10.4s,制动时间t8=5.2s,此过程中自由落体过程中下降的高度:h3=70.3m。
3.5 嫦娥三号软着陆轨道设计与控制策略
六个阶段控制策略如表1所示:

表1 嫦娥三号软着陆控制策略表
4 误差与灵敏度分析
4.1 误差分析
本文用实际着陆点和预定着陆点的直线距离来刻画偏离预定着陆点位置的程度。
在快速调整阶段,距月球表面2400米高度时水平方向产生的偏差:
x1=859.8-464.93=394.87m
在避障阶段(包括粗避障和精避障),实际着陆点与预定着陆点之间的水平距离x2=5m,垂直距离x3=5.5m
4.2 敏感度分析
在粗避障与精避障阶段,改变μ1,μ2的值,可得不同的筛选数量,见表2:
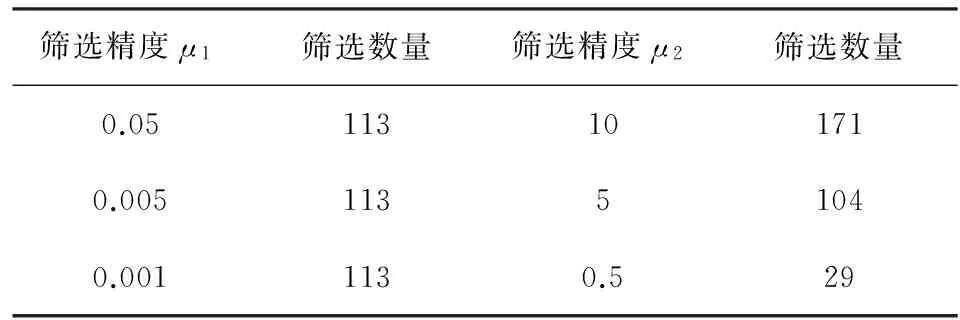
表2 粗避障与精避障筛选精度与筛选数量关系表
参数μ1的敏感度为0。
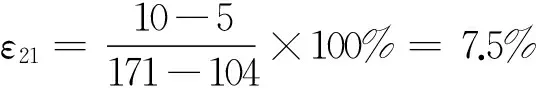

[1]BonfiglioEP,AdamsD,CraigL,etal.LandingsitedispersionanalysisandstatisticalassessmentfortheMarsPhoenixLander[C]//AstrodynamicsSpecialistConferenceandExhibit.Hawaii:AIAA,2008:7348.
[2]KubotaT,HashimotoT,KawaguchiJ,etal.GuidanceandnavigationofHayabusaspacecraftforasteroidexplorationandsamplereturnmission[C]//InternationalJointConference.Busan:SICE-ICASE,2006:2793-2796.
[3] 刘少创,贾阳,马友青,等.嫦娥三号月面巡视探测器高精度定位[J].科学通报,2015(4):372-378.
[4] 赵育善,师鹏.航天器飞行动力学建模理论与方法[M].北京:北京航空航天大学出版社,2012:85-115.
[5] 吴沧浦,夏元清,杨毅.最优控制的理论与方法[M].北京:国防工业出版社,2013:105-134.
[6] 胡寿松,王执铨,胡维礼.最优控制的理论与系统[M].北京:科学出版社,2005:46-76.
[7] 马明亮,王超,施润和,等.嫦娥一号IIM高光谱数据和月球轨道器LOLADEM数据的配准与月表地形校正及评价[J].地球信息科学学报,2015(1):118-125.
[8] 李培佳,黄勇,昌胜骐,等.基于地基观测的嫦娥三号着陆器与巡视器高精度定位[J].科学通报,2014(32):3162-3173.
[责任编辑、校对:周 千]
Trajectory-design and Control-strategy of Chang'E-3 Soft-landing
YANGYong-hui1,LIURui2,LIHua2
(1.Northwest Institute of Nuclear Technology, Xi'an 710024,China;2.Faculty of Science, Xi'an Aeronautical University, Xi'an 710077, China)
In this paper, the trajectory-design and control-strategy of the Chang'E-3 soft-landing is studied.At first, the relative velocity and position at the pericynthion and apocynthion are given by Kepler's first and second laws.Then, the Chang'E-3 soft-landing process is divided into six phases.For every phase, the optimization model whose object is minimum fuel consumption is found by the dynamic differential equation.We get the ignition time and thrust of six phases by switch control theory and minimal value principle.At last, it is concluded through stability analysis that the trajectory-design and control-strategy of the Chang'E-3 soft-landing in this paper has advantages such as smaller error and lower sensitivity.
switch control theory; smoothness matrix; search algorithm
2015-03-26
杨永辉(1980-),男,山西闻喜人,工程师,从事空间技术方面的研究。
V
A
1008-9233(2015)03-0014-06

