环形信号交叉口进口道车辆延误及排队长度计算方法*
丁柏群 裴 煦
(东北林业大学交通学院 哈尔滨150040)
0 引 言
环形交叉口是在几条道路相交的交叉口中央,设置圆形中心岛或带圆弧形状的中心岛,使进入交叉口的所有车辆均以逆时针方向(靠左行驶情况下为顺时针)绕岛行驶,其运行过程一般为先在不同方向汇合(合流),接着于同一车道先后通过(交织),最后分向驶出(分流)。同一般平面交叉口相比,环形交叉口具有冲突点少、车流连续、行驶安全等优点。
随着近年来城市交通拥挤问题不断严峻,各个环形交叉口也经常出现交通需求大于交通供给的现象。很多城市采取拆除环形交叉口,改建成一般信号控制平面交叉口的办法来增加路口通行能力。然而,在我国许多城市环形交叉口经常建设有城市地标性建筑景观,该环岛需要保留。因此,许多专家寻求将传统环形交叉口改造为信号控制环形交叉口,这一措施已经在我国普遍推广应用。
分析环形交叉口的车辆延误、排队长度是合理评价其服务水平的基础。总体来说,环形交叉口服务水平分析的代表性方法有以下3类:①美国《道路通行能力手册》(HCM)[1-2],HCM 把延误作为评价交叉口服务水平的重要标准之一,通过采集美国各个环形交叉口的延误数据进行分析,采用类似于无信号控制交叉口的方法进行交叉口车辆延误估计,但其理论性较为欠缺;②由澳大利亚ARRB开发的用于设计和评估交叉口的辅助工具SIDRA 软件包[3-5],该软件包适用于全向停让控制交叉口、双向停车控制交叉口、信号控制交叉口和环行交叉口等;③杨晓光等[6-8]人提出了基于HCM的改进环形交叉口车均延误模型法,以车均延误最小为目标得到最佳信号周期,此模型在国内使用较为广泛,但其对于环形信号交叉口延误计算的可靠性尚有待研究。此外,一些学者对信号控制下的环形交叉口进行了分析,如左俊中等[9]提出的环交信号控制方法对环内车辆冲突点进行了分析,针对单口放行时控制方法进行优化;徐洪峰也对单口轮流放行情况下的环形信号交叉口最佳信号周期进行优化[10];丰晓芳、郭瑞军等[11-12]基于环形交叉口车流特性提出了较可行的延误模型。
上述方法一般适用于无信号环形交叉口。由于信号控制与无信号环形交叉口在车辆运行特性方面存在的显著差异,在使用现有的延误和排队长度计算模型时,需要考虑环形信号控制交叉口的具体特征进行改进,以符合工程实际。此外,环形交叉口的相位相序设计方案对交通流运行也存在重要影响,以往的研究成果中未进行考虑。本文以两车道环形交叉口为研究对象,采用解析法建立环形交叉口进口道内侧与外侧车道车辆延误及排队长度模型,为环形信号交叉口交通组织优化、服务水平评价奠定理论基础。
1 延误与排队长度影响因素分析
1种典型的信号控制环形交叉口如图1所示。该交叉口包括4个入口,每个入口有2条进口车道,在进口车道停车线处设置1个信号灯,以控制车辆的运行。对于图1所示的十字环形交叉口,常见的相位相序方案有2种,分别为单口轮流方向和对称放行,见图2。
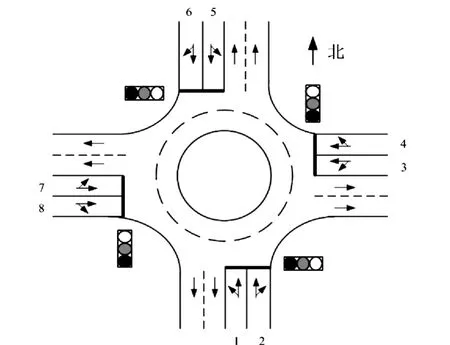
图1 环形交叉口信号控制示意图Fig.1 Roundabout signal control schematic
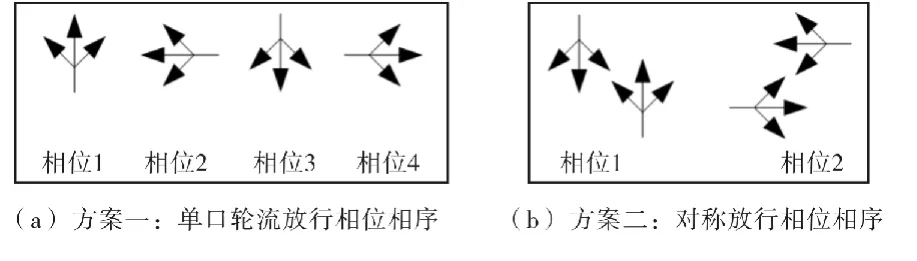
图2 典型环形交叉口相位方案Fig.2 Typical phase program Roundabout
环形信号交叉口车辆延误、排队长度的主要影响因素包括:
1)信号配时参数。单个环形信号交叉口的信号配时参数主要包括周期时长、各相位绿灯时间。这些参数直接决定了各个入口的通行能力、车辆释放规律,进而影响到达机动车的延误以及排队长度。显然,每个相位的绿信比越大,则该相位所控制的各个入口的车道通行能力越大。
2)相位相序方案。见图2,当环形交叉口采用相位方案一时,各个入口的交通流在驶入环道时不存在环内车辆的阻碍;而当采用相位方案二时,对向的左转机动车会阻碍本入口的机动车驶入(如北入口的左转车影响南入口的机动车);而且左转车流量越大,本入口可以驶入环内的机动车越少,那么延误与排队长度越大。
3)道路交通渠化。以图1南入口的2条进口车道为例,当信号灯变为绿灯后,车道1的交通流驶入环道需要穿越环道内2条车道上的交通流,寻找可穿越间隙的情况下完成驶入。而车道2的交通流驶入环道,只需要穿越环道内外侧车道上的交通流。由此可见,不同的道路渠化方案(车道数量、车道属性)对机动车的延误与排队长度产生重要影响。
笔者在考虑上述3个影响因素基础上,以图2所示的2进口车道环形交叉口为例,阐述不同相位相序方案下,信号配时参数与延误、排队长度的关系模型。
2 相位方案1下的延误与排队长度计算
以图1南入口的2条进口车道为例,将车道1称为内侧车道,车道2称为外侧车道。下面分别研究2个车道的延误、排队长度计算模型。
2.1 内侧进口道车均延误与排队长度计算
在相位方案1下,设车道i的机动车到达率为qi,相位i的绿灯时间为gi,绿灯间隔时间为Ii,那么交叉口周期时长C等于:
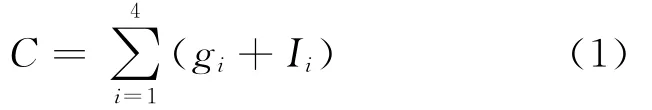
式中:gi为相位i的绿灯时间,s;I为绿灯间隙时间,s。
当相位1的绿灯启亮后,车道1的机动车开始进入环岛。由于此时环岛内的2条车道上不存在其他入口驶入的机动车,所以车道1的机动车可以直接驶入环岛。在这种情况下,其延误与排队理论模型可以参考十字信号交叉口的计算方法。即:
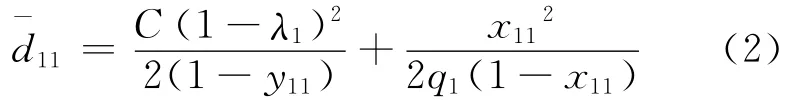

式中:S11为相位1对应的进口车道1的饱和流率;Cap1为进口车道1的通行能力。
相位1绿灯开始时,车道1停车线后排队长度为:
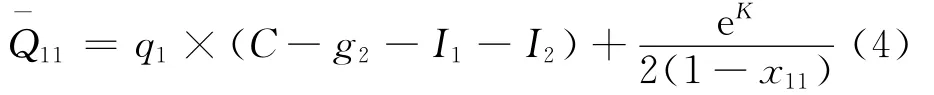
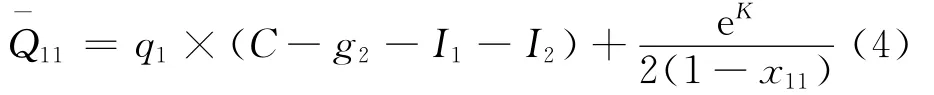
2.2 外侧进口道车均延误与排队长度计算
在相位方案1下,南入口外侧车道(车道2)的运行也不受环内车辆的阻碍,能够顺畅地驶入环岛,其车均延误与排队长度的计算可以参考2.1节。
3 相位方案2下的延误与排队长度计算
在相位2方案下,每个信号相位控制2个入口的交通流。以相位1为例,当该相位绿灯启亮后,南、北2个入口的交通流可以驶入环岛。左转交通流一般行驶在环岛中的里侧车道。根据交通规则,当北入口的左转机动车行驶到南入口附近时,南入口的机动车需要停车让行,此时南入口内侧车道(车道1)的机动车无法驶入环岛,外侧车道(车道2)的机动车可以驶入;同理,当北入口的左转机动车行驶到北入口附近时,北入口内侧车道(车道5)的机动车无法驶入环岛,车道6的机动车可以驶入。具体如图3所示。此时进口车道机动车的延误、排队长度计算与相位方案1下的计算存在显著差异。

图3 相位方案2下的机动车运行示意图Fig.3 Vehicle operation schematic diagram in the second phase of the program
3.1 内侧进口道车均延误与排队长度计算
仍以相位1为例进行分析。设相位1显示绿灯期间,南入口车道1有N1L辆左转机动车驶入环岛,北入口车道5有N5L辆左转机动车驶入环岛。每个周期车道1、车道5到达的机动车辆数A1,A5,可以采用公式(5),(6)计算。

在到达的机动车中,车道1、车道5的到达直行车和左转车分别等于:

式中:q1L为进口车道1的左转机动车到达流量;A1L为进口车道1每周期到达的左转机动车辆数;A1T为进口车道1每周期到达的直行机动车辆数。其他参数类推。
当A5L辆左转机动车行驶到南入口附近时,车道1的机动车需要让行。设每辆机动车的跟随车头时距为Δt1,那么在相位1显示绿灯期间,车道1的机动车累积需要让行时间gr11可以采用下式计算:

即在相位1显示g1秒绿灯期间,车道1可以利用的绿灯时间为(g1-),则实际有效绿信比λr11:
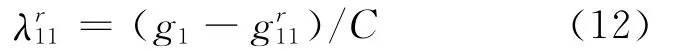
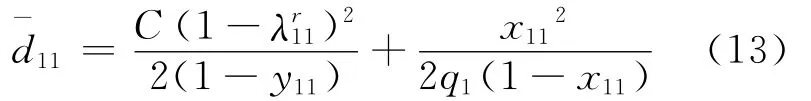
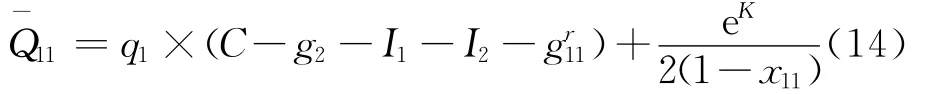
同理,北入口车道5的机动车需要让行南入口驶入的左转机动车时间为(A1L×Δt)。车道5的机动车车均延误与排队长度计算方法可以借鉴式(13),(14)。由前面的叙述可知,式(13),(14)的关键是获得A1L,A5L,可以通过在环形交叉口布设多组感应线圈的方式检测上述2个参数;或者布设视频检测器,通过提取、对比车辆牌照的方法得到车辆行驶轨迹,判别其流向。
3.2 外侧进口道车均延误与排队长度计算
以南入口为例进行分析,当北入口的左转机动车行驶到南入口附近时,南入口外侧进口车道(车道2)的机动车无需让行,可以继续驶入环岛。但是当该机动车与北入口驶入的左转车相遇时,二者将产生冲突。一般来讲,如果北入口左转机动车先到达冲突点,则它具有优先级,否则需要让行车道2驶入的机动车。当车道2的机动车让行北入口的左转机动车时,需要停车等待,并阻碍车道2后续机动车的释放,增加延误与排队长度。
交通流的到达具有随机性。当上述2股交通流发生冲突时,有可能出现车道2驶入的机动车让行全部北入口的左转机动车,也有可能出现全部北入口的左转机动车让行车道2驶入的机动车。车道2无法利用的绿灯时间为0.5A5L×Δt1。之所以引入系数0.5是因为冲突情况下存在2股交通流存在各种让行可能,所以取其平均值,即车道2驶入的机动车会让行50%的北入口左转车。

然后可以借鉴式(13),(14)计算车道2的车均延误、排队长度。
4 案例分析
为了对2、3节所建立的模型精度进行验证,以哈尔滨市博物馆环形交叉口为例进行案例分析,见图4。该环形交叉口地处市区大直街与中山路2条主轴线道路的交接处,是城市骨架道路网的重要枢纽之一。博物馆环形交叉口地面部分由4个主要进出口引道和2个次要进出口引道组成,是1个不规则多路环形交叉口,其中满洲里街与海关街对整个环形交叉口的影响较小。
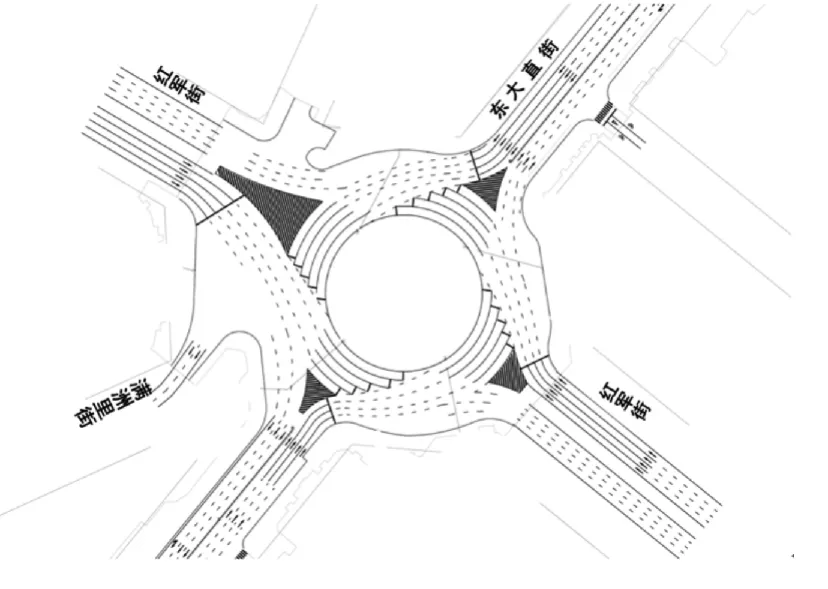
图4 哈尔滨博物馆环形交叉口渠化方案Fig.4 Harbin City Museum Roundabout drainage scheme
4.1 交通调查
对博物馆环形交叉口周边路口的交通量、流向进行了连续12h观测(2014年4月),调查中观测间隔为15min,大型车、中型车、小型车的折算系数为2.0∶1.5∶1.0。博物馆环形交叉口折算后每小时进口交通量汇总后见图5。
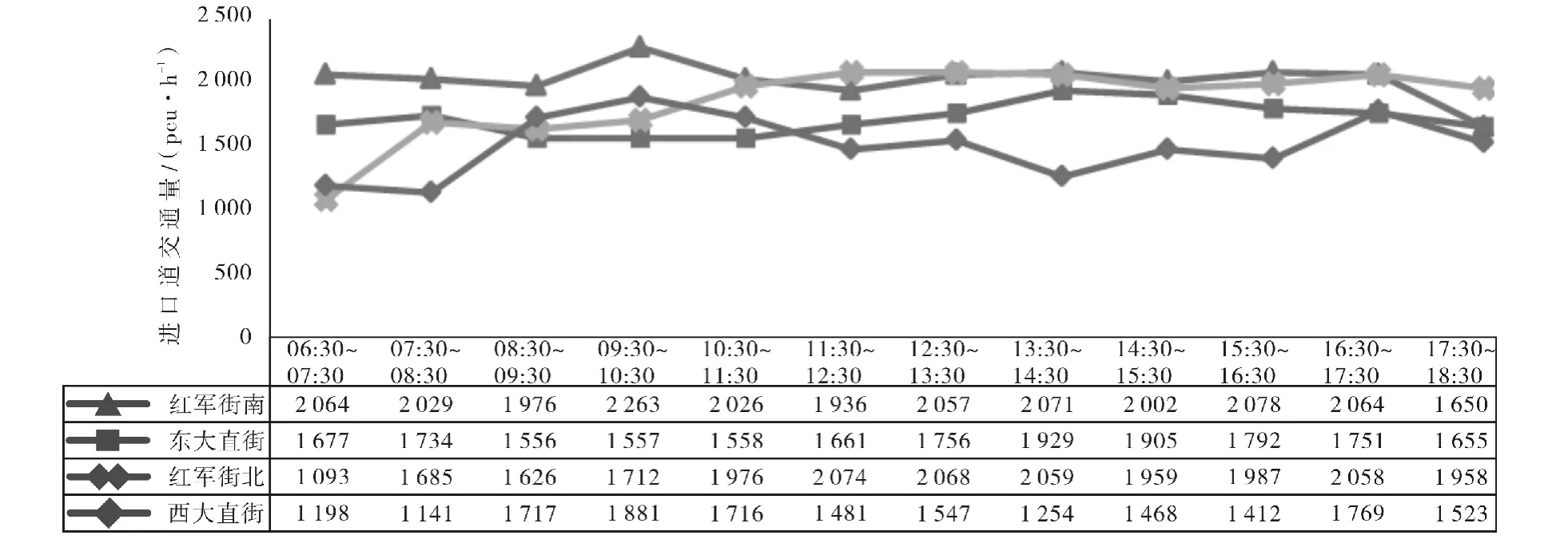
图5 博物馆环形交叉口各进口道交通量Fig.5 The road traffic imports in Museum Roundabout
4.2 仿真实验
依据调查数据,利用交通微观仿真软件Vissim对博物馆环岛高峰时段交通运行现状和实施改善措施后的交通运行状况分别进行了仿真。具体仿真过程如图6所示。
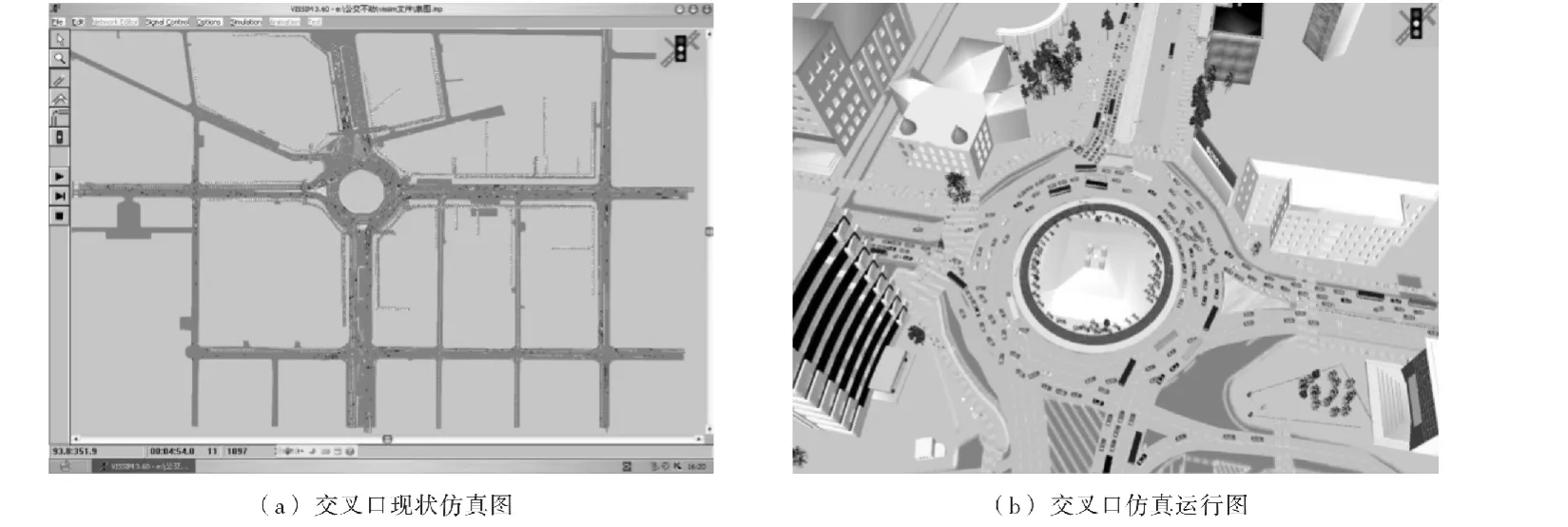
图6 交叉口现状仿真图Fig.6 Museum Roundabout situation situation simulation map
由于满洲里街与海关街交通流量非常小,在设计信号方案过程中不进行考虑。针对4个主要出入口,采用图2中的相位方案2,即对称放行的方法。在Vissim中进行VAP编程,设计感应信号控制方案,当每个相位对应的车道连续5s绿灯期间无机动车到达时,将绿灯切换至下1个相位。2个相位的最小绿灯时间设置为15s,最大绿灯时间设置为70s,绿灯间隔时间3s。
模型结果与仿真输出结果见表1。

表1 博物馆环形交叉口车辆平均延误及平均排队长度Tab.1 Museum Roundabout average vehicle delay and average queue length
通过对本文模型计算结果与仿真输出结果进行对比,发现车均延误的平均误差值为10.4%,排队长度的平均误差值为12.3%,结果基本相近。这表明所提出的理论模型具有实际应用的可信性和可行性。
5 结束语
环形信号交叉口的车辆延误、排队长度指标计算是进行服务水平评价、信号配时方案优化的基础。笔者考虑了信号配时参数、道路渠化、相位相序方案的影响,分别建立了进口道内侧车道、外侧车道的车辆延误、排队长度计算模型。以哈尔滨市的实际环形交叉口为例对模型进行了验证,表明所提出的理论模型具有实际应用价值。
为了建模的方便,笔者以2个入口车道环形交叉口为例进行阐述,模型的推导过程可以扩展应用到具有多个(大于2个)入口车道的环形交叉口。
[1] Transportation Research Board.National research council.highway capacity manual[M].Washington D.C.:TRB,2010.
[2] FLANNERY A,ELEFTERIADOU L.Safety delay and capacity of single-lane roundabouts in the United States[J].Transportation Research Record:Journal of the Transportation Research Board,1998(1646):63-70.
[3] EEASA D.Proposed geometric features to improve safety of modern roundabouts[C].Transportation Research Board 85fh Annual Meeting.2006,Washington D.C.:TRB,2006.
[4] HE Q,HEAD K L,DING J.Multi-modal traffic signal control with priority,signal actuation and coordination[J].Transportation Research Part C:E-merging Technologies,2014(46):65-82.
[5] 于少伟,史忠科.信号交叉口集聚车辆跟驰模型[J].中国公路学报,2014,27(11):94-100.YU Shaowei,SHI Zhongke.Car-following model on vehicles arrival during the red phase[J].China Journal of Highway and Transport,2014,27(11):94-100.(in Chinese)
[6] 杨晓光,赵靖,汪涛.环形交叉口信号控制最佳周期计算方法[J].中国公路学报,2008,21(6):90-95.YANG Xiaoguang,ZHAO Jing,WANG Tao.Optimal Cycle Calculation Method of Signal Control at Roundabout[J].China Journal of Highway and Transport,2008,21(6):90-95.(in Chinese)
[7] 王炜.道路平面交叉口通行能力的延误分析法[J].中国公路学报,1998,11(2):62-67.WANG Wei.Analysis method for capacity of road junctions based on the delay-curve[J].China Journal of Highway and Transport,1998,11(2):62-67.(in Chinese)
[8] 马万经,杨晓光.信号控制交叉口实时延误计算与仿真研究[J].交通与计算机,2006,24(3):1-4.MA Wanjing,YANG Xiaoguang.Real-time delay model and simulation for signalized intersection[J].Computer and Communications,2006,24(3)1-4.(in Chinese)
[9] 左俊中,徐良杰,倪龙和.基于单口放行的四路环交信号控制优化方法[J].公路交通科技,2013,30(4)88-93.ZUO Junzhong,XU Liangjie,NI Longhe.An optimization method of signal control at 4-leg roundabout based on single release[J].Journal of Highway and Transportation Research and Development,2013,30(4):88-93.(in Chinese)
[10] 徐洪峰,耿现彩,何 龙.单进口轮流放行方式的四路环形交叉口交通信号控制[J].吉林大学学报:工学版,2014,44(4):953-962.XU Hongfeng,GENG Xiancai,HE Long.Signal timing plan for fully signalized four-leg roundabouts with single-approach-entering operation[J].Journal of Jilin University:Engineering and Technology Edition,2014,44(4):953-962.(in Chinese)
[11] 丰晓芳,常玉林.公路环形交叉口延误模型研究[J].交通信息与安全,2010,28(3):63-67.FENG Xiaofang CHANG Yulin.Delay model of highway roundabouts[J].Journal of Transport Information and Safety,2010,28(3)63-67.(in Chinese)
[12] 郭瑞军,林柏梁.环形交叉口交织区车流运行特性的研究[J].交通运输系统工程与信息,2010,10(3):29-34.GUO Ruijun,LIN Bo-liang.Traffic operation performances at roundabout weaving sections[J].Journal of Transportation Systems Engineering and Information Technology,2010,10(3):29-34.(in Chinese)

