Frame length optimization for multi-antenna downlink systemsbased on delay-bound violation probability constraints

Tan Yufeng Li Junchao Xia Weiwei Shen Lianfeng

(National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)



Frame length optimization for multi-antenna downlink systemsbased on delay-bound violation probability constraints

Tan Yufeng Li Junchao Xia Weiwei Shen Lianfeng

(National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)

A frame length optimization scheme is proposed for multi-antenna downlink systems to guarantee diverse delay-bound violation probability constraints. Due to the difficulties of extracting the quality of service (QoS) metrics from the conventional physical-layer channel models, the link-layer models named effective bandwidth and effective capacity are applied to statistically characterize the source traffic patterns and the queuing service dynamics. With these link-layer models, the source traffic process and the channel service process are mapped to certain QoS parameters. The packet delay-bound violation probability constraints are converted into minimum data rate constraints and the optimization problem is thus formulated into simultaneous inequalities. With the assumption of ergodic block-fading channels, the optimal frame lengths of single-user and multiuser systems are calculated respectively by numerical iterative methods. Theoretical analyses and simulation results show that the given delay-bound violation probability constraints are well satisfied with the optimal frame length.

delay-bound violation probability; frame length optimization; effective bandwidth; effective capacity; multi-antenna systems; quality of service

The last decade has seen an explosive growth in multimedia applications, which brings an unprecedented demand for wireless network performance enhancement to support high-data-rate services with a diverse quality of service (QoS) requirements. In multi-antenna systems, guaranteeing heterogeneous QoS to multiple users arouses great concern and remains challenging due to the time-varying fading channel, the co-channel interference (CCI) and resource competition among users. Note that the frame length of the downlink of multi-antenna systems has an obvious impact on the system throughput, where a trade-off exists between the multiuser diversity gain by choosing smaller frame lengths and the throughput improvement by making frames larger.

The frame length optimization problem has been studied separately at the physical (PHY) layer and the media access control (MAC) layer. The orthogonal frequency division multiplexing (OFDM) systems were studied in Refs.[1-3]. A optimized data transmission scheme was proposed by optimizing the auxiliary signaling interval to maximize the amount of payload data transmitted[1], while the optimal frame size is selected with concern regarding maximizing the spectrum efficiency[2]. Besides, Wu et al.[3]formulated the system efficiency as a function of the frame length, scheduling cost and channel conditions, and then found the optimal frame length by dynamic programming algorithms. On the other hand, this problem was investigated from the MAC-layer perspective in Refs.[4-6]. Iqbal et al.[5]studied the tradeoff between reliability and frame length with the redefined reliability function for the binary symmetric channels and theK-th order Markov channels. In Ref.[6], the slot allocation and frame length of ad hoc networks were jointly optimized through a decentralized TDMA-based MAC-layer scheduling protocol to maximum the slot reuse. However, instead of complex upper-layer QoS guarantees, the above schemes were evaluated based on the PHY-layer parameters including the bit error rate (BER) or the frame error rate (FER). Furthermore, users or terminals were described in terms of the signal-to-noise ratio (SNR) rather than statistical traffic characteristics. There remains a lack of cross-layer analysis on frame length optimization problems with diverse QoS constraints as well as appropriate traffic statistics and channel behavior characterization for multi-antenna systems.

In this paper, we seek to guarantee reliable transmission under the maximum tolerable delay-bound violation probabilities by optimizing the frame length of multi-antenna downlink systems. We study the frame length optimization problem with a joint consideration of the transmission rates at the PHY layer and diverse QoS requirements at the MAC layer. First, the source statistics and the queue dynamics are both incorporated, where the data sources are modeled as discrete-time, finite state, irreducible, stationary Markov chains, and the queue service is characterized by the functions mapped to the link-level QoS guarantees. Different from the conventional PHY-level channel models which characterize the fluctuations in the amplitude of the radio signal, the concepts of effective bandwidth and effective capacity[7-9]are applied to illustrate the source traffic pattern and channel behavior, respectively. Secondly, the maximum tolerable delay-bound violation probabilities are converted into data rate constraints. Then, the cross-layer frame length optimization problem can be expressed as functions of source traffic parameters, QoS requirements and data rates. With certain source traffic models and QoS parameters, the optimal frame length can be calculated. As a result, reliable transmission under certain delay-bound violation probability constraints is guaranteed, while the quantitative relationship between the optimal frame length and QoS requirements is revealed.

1 System Model and QoS Guarantees

1.1 System model

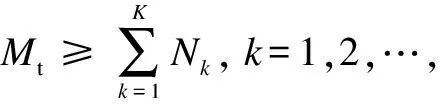
Fig.1 Multi-antenna broadcast system with precoding and perfect CSI feedback

(1)

wherenk∈CNk×1denotes the additive white Gaussian noise (AWGN) with zero mean and the covariance matrixσ2INk.

With perfect knowledge of CSI, we can cancel inter-user interference, the second term in Eq.(1), by appropriately designing the precoding matrices. After that, the multiuser multiple-input multiple-output (MIMO) channel is decomposed intoKparallel noninterfering single-user MIMO links. According to prior analysis of the MIMO channel capacity, the achievable rate of thek-th user is given by

(2)

where {pn,k,n=1,2,…,mk} denote the SNR per receiving antenna under unity channel gain for the individual data substreams of thek-th user and {σn,k,n=1,2,…,mk} are nonzero singular values of the equivalent channel matrixHkWkwithmk=rank(HkWk). The equal power allocation to the transmit antennas is adopted instead of an adaptive power distribution strategy for the purpose of simplification, replacingpn,kwithp.

1.2 Descriptions of QoS guarantees

Generally, QoS parameters at the MAC layer or upper layers are referred to delay bounds or delay jitter for a certain minimum rate, while those at the PHY layer are represented by SNR, BER at the receiver. In this paper, we assume a time-slotted packet communication model without the automatic repeat request (ARQ) protocol. For each user, packets generated by the source are sequentially stored in a queue in the transmit buffer and grouped into frames before being served in a first-come-first-serve manner. LetTbe the frame or time slot duration mentioned earlier. To characterize the burstiness of the arrival traffic, we assume that the arrival stream {At} is modulated by a discrete-time, finite state, irreducible, stationary Markov chain {Xt} with the state spaceSand the transition matrixQ=(qij),i,j∈S. Thus, the distribution ofAtat timetdepends only on the source stateXtand theAt’s are independent while in one state of the chain. Consider a two-state ON-OFF Markov chain with exponentially distributed ON and OFF period as the traffic source in this paper. The number of packets generated per time slot during ON state follows an independent Poisson distribution of rateαkand each packet has a fixed sizeNbin bits.

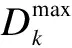
(3)

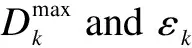
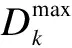
(4)

exists and is finite, differentiable for all realzk, hereE{·} is the expectation operator.

(5)

where the expectationEHk{·} is with respect to all channel states.

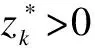
(6)

then the left-hand term of constraint (3) can be appropriately approximated as

(7)

Assume that the arrival rates of the traffic source are large enough so that the buffer is always non-empty, with Pr(Dk>0)=1. Hence, a necessary and sufficient condition for constraint (3) is

(8)

Consequently, the delay-QoS requirements of the user can be guaranteed.

2 Analysis of Frame Length Optimization

2.1 Single-user systems

We first focus on the case where the multi-antenna downlink system is single-user. According to the system model, we can derive the degenerate model in a point-to-point communication system ofMttransmit andNkreceiving antennas

yk=Hkxk+nk

forHk∈CNk×Mt,xk∈CMt×1andyk,nk∈CNk×1. With a singular value decomposition (SVD), the achievable rate of Eq.(2) can be simplified as

(9)

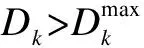
(10)

For any discrete-time Markov modulated process, letGi(z)=E{exp(zAt)|Xt=i} be the generating function of the conditional distribution ofAtwith the source stateXt=i. With the constructed matrixU(z)=[qijGi(z)], the GE limit for a Markov source is[11]

(11)

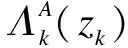
(12)

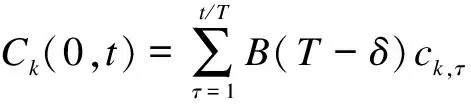
(13)

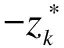
(14)

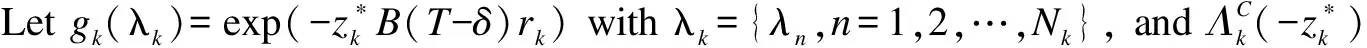
(15)

wherefk(λk) is the joint probability density function ofλk. As a result, the GE limit of the accumulative service process can be calculated by iterative methods.

2.2 Multiuser systems

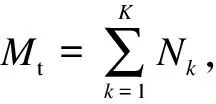
(16)

(17)

whereVk∈CNk×Mtis an upper triangular matrix andΘk∈U(Mt,Nk).U(Mt,Nk) is the collection ofMt×Nkcomplex matrices with unit-norm orthogonal columns. Without eigenmode selection performed by extra transmit antennas, we can write the precoding matrixWkas

(18)

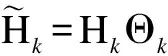
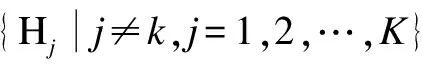
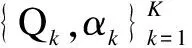
It is finally proven that the frame length optimization problem of multiuser systems is an extension of the single-user case. Thus, the optimal frame length region is defined as the intersection of allKframe length regions of each user,

(19)

whereTkis determined by Eqs.(6) and (8). The optimal frame length of multiuser systems is given by

(20)

3 Numerical Results and Simulation

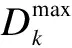
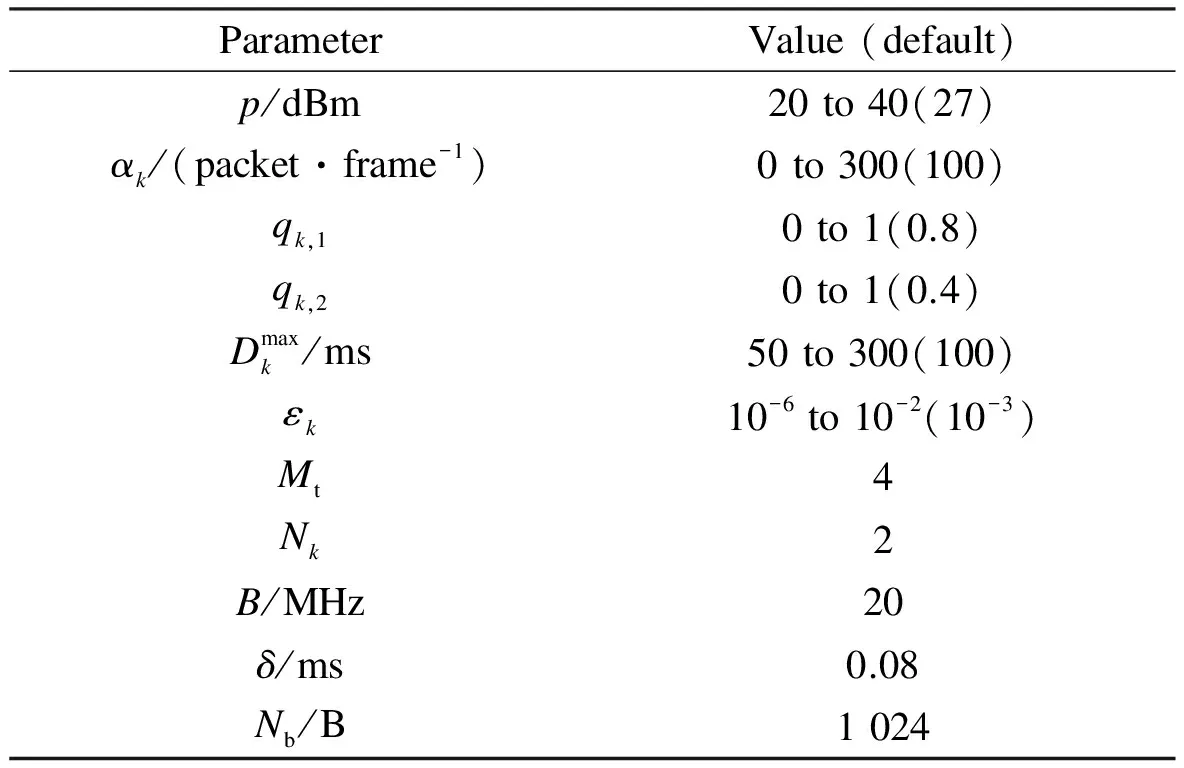
Tab.1 Simulation parameters

3.1 Effect of traffic source parameters

We validate the effect of traffic source parameters on delay-bound violation probability as a function of frame length. The theoretical values of the optimal frame length are numerically calculated by Eq.(10), as shown in Tab.2.

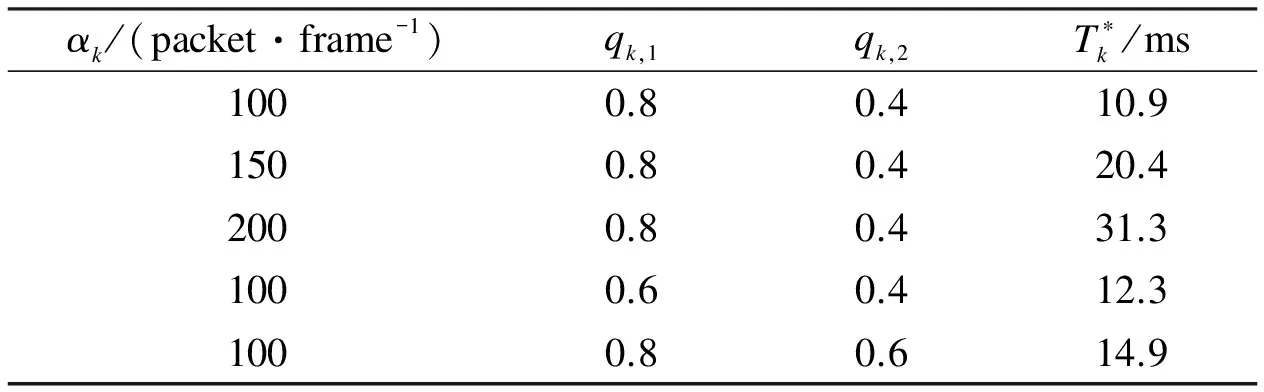
Tab.2 Traffic parameters and theoretical optimal frame length values

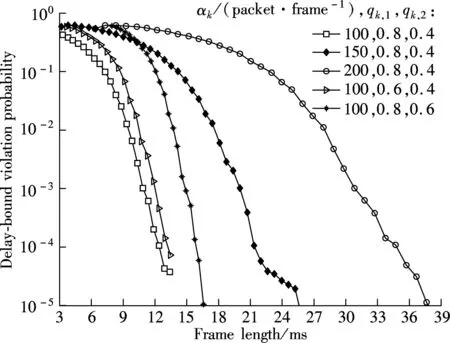
Fig.2 Delay-bound violation probability vs. frame length of traffic source parameters

3.2 Effect of delay-QoS requirements

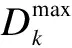
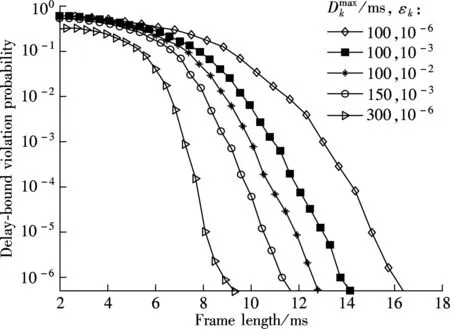
Fig.3 Delay-bound violation probability vs. frame length of different and εk

Fig.4 Delay-bound violation probability vs. frame length of different

Tab.3 Delay-QoS requirements and theoretical optimal frame length values

3.3 Delay-bound violation probabilities of different SNR

In order to validate the effects of SNR on the proposed frame length optimization scheme, the curves of the delay-bound violation probability vs. frame length are plotted with different SNR values in Fig.5. A highly acceptable agreement can be observed between theoretical results and the simulation. Similar to the results in Tab.4, the lower SNR results in a larger frame, given certain delay-bound violation probability constraints. As the frame length changes, delay-bound violation probabilities of the higher SNR become more sensitive than those of the lower SNR due to larger frames can be more efficient than smaller frames in consideration of the overhead.

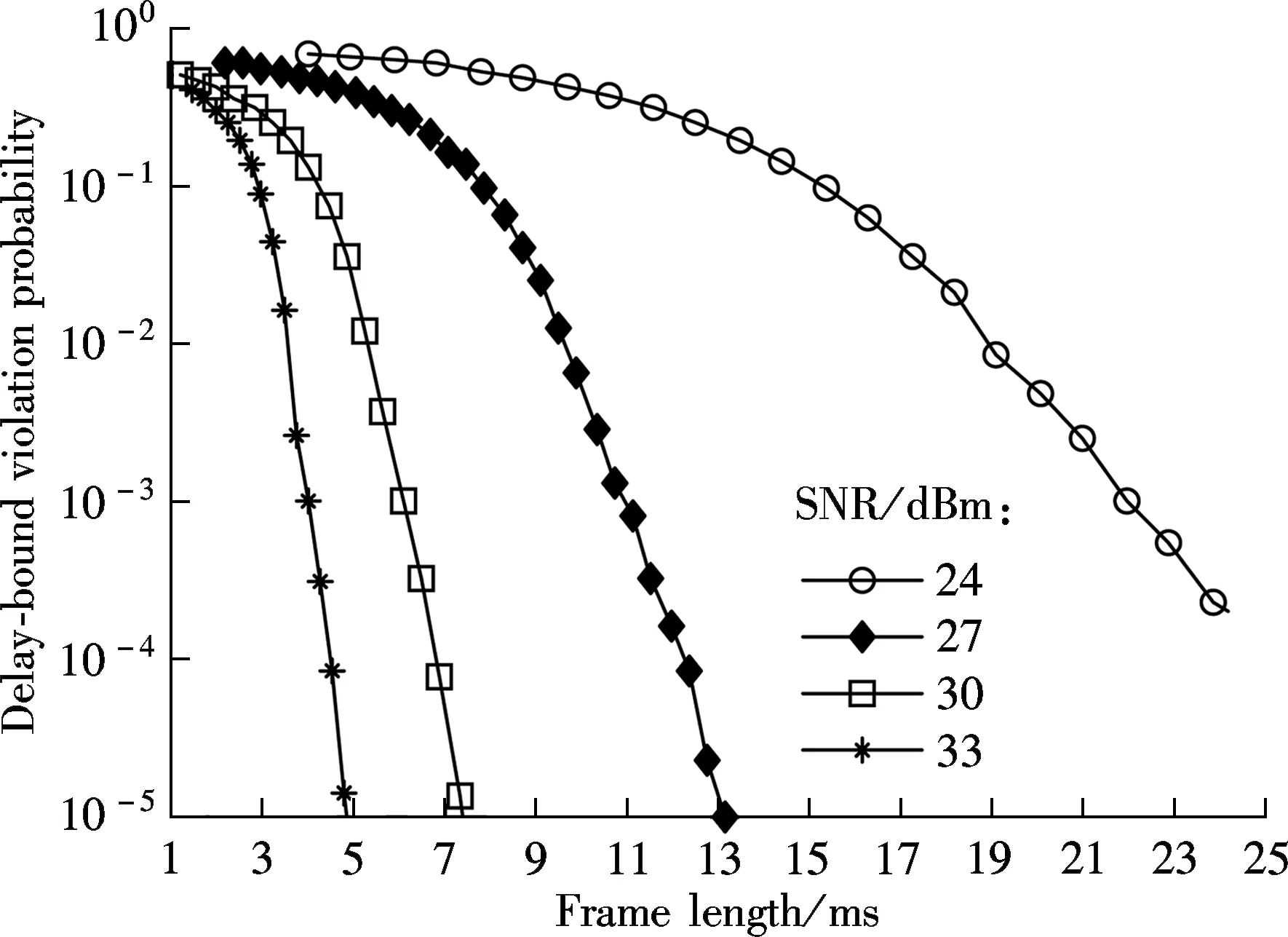
Fig.5 Delay-bound violation probability vs. frame length of different SNR

Tab.4 SNR values and theoretical optimal frame length results

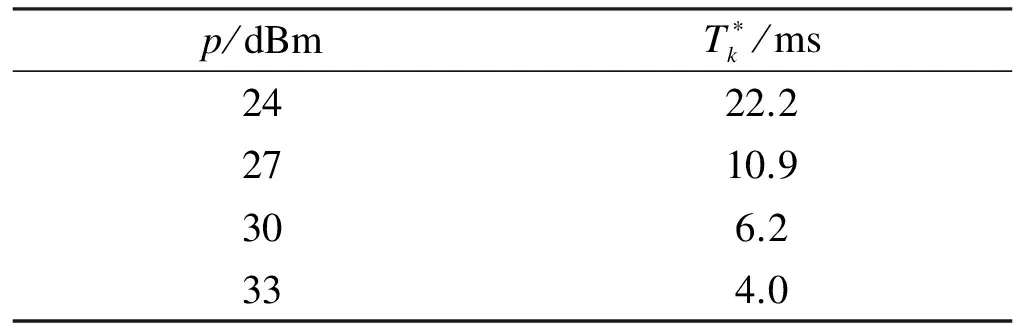
p/dBmT∗k/ms2422．22710．9306．2334．0

4 Conclusion

In this paper, a frame length optimization scheme is proposed for multi-antenna downlink systems to guarantee diverse delay-bound violation probability constraints. Concepts of effective bandwidth and effective capacity are applied to characterize the traffic source pattern and the queuing service dynamics. Different link-layer delay-QoS requirements are converted into PHY-layer data rate constraints. The cross-layer optimization of frame length is expressed as functions of traffic source parameters, delay requirements and data rates. The proposed scheme optimizes frame lengths of single-user and multiuser systems over flat Rayleigh fading channels. Theoretical analyses and simulation results show that delay-bound violation probability constraints can be well satisfied with the optimal frame lengths. Since the optimal frame length is designed without traffic scheduling, it is of interest to develop optimization schemes under overloaded scenarios.

[1]Trifonov P. Optimization of the downlink frame length in adaptive systems [C]//2005IEEE7thCASSymposiumonEmergingTechnologies:CircuitsandSystemsfor4GMobileWirelessCommunications. St. Petersburg, Russia, 2005: 50-53.

[2]Keum Seung Won, Kim Jeong Gon. Decision of frame size and radio resource allocation for OFDMA/TDD-based next generation cellular systems [C]//2007InternationalConferenceonConvergenceInformationTechnology. Gyeongju, Korea, 2007:984-989.

[3]Wu Yi, Tang Zhiqiang, Larsson E G. Optimization of frame length in OFDMA systems taking into account the control signaling cost [C]//2011IEEE73rdVehicularTechnologyConference(VTCSpring). Yokohama, Japan, 2011: 1-5.

[4]Lettieri P, Srivastava M B. Adaptive frame length control for improving wireless link throughput, range, and energy efficiency [C]//IEEE17thAnnualJointConferenceoftheIEEEComputerandCommunicationsSocieties. San Francisco, CA, USA, 1998: 564-571.

[5]Iqbal A, Qureshi H K, Saleem M, et al. On the tradeoff between reliability and frame length in wireless networks [C]//ThirdInternationalConferenceonNextGenerationMobileApplications,ServicesandTechnologies. Cardiff, Wales, 2009: 265-270.

[6]Chaudhary M H, Scheers B. Progressive decentralized TDMA based MAC: joint optimization of slot allocation and frame lengths [C]//2013IEEEMilitaryCommunicationsConference. San Diego, CA, USA, 2013: 181-187.

[7]Wu Dapeng, Negi R. Effective capacity: a wireless link model for support of quality of service [J].IEEETransactionsonWirelessCommunications, 2003, 2(4): 630-640.

[8]Davy A, Meskill B, Domingo P J. An empirical study of effective capacity throughputs in 802.11 wireless networks [C]//2012IEEEGlobalCommunicationsConference. Anaheim, CA, USA, 2012: 1770-1775.

[9]Anwar A H, Seddik K G, ElBatt T, et al. Effective capacity of delay constrained cognitive radio links exploiting primary feedback [C]//11thInternationalSymposiumonModeling&OptimizationinMobile,AdHoc&WirelessNetworks. Tsukuba, Japan, 2013: 412-419.

[10]Chang C S.Performanceguaranteesincommunicationnetworks[M]. Berlin, Germany: Springer-Verlag, 2000.

[11]Harsini J S, Lahouti F. Adaptive transmission policy design for delay-sensitive and bursty packet traffic over wireless fading channels [J].IEEETransactionsonWirelessCommunications, 2009, 8(2): 776-786.

[12]Kuo Ping Heng, Smith P J, Garth L M. Joint density for eigenvalues of two correlated complex Wishart matrices: characterization of MIMO systems [J].IEEETransactionsonWirelessCommunications, 2007, 6(11): 3902-3906.

基于超时违约概率约束的多天线系统下行帧长优化

谭雨凤 李俊超 夏玮玮 沈连丰

(东南大学移动通信国家重点实验室, 南京 210096)

为了满足数据传输的时延约束,提出一种多天线系统的下行帧长优化方案.由于传统的物理层信道模型在评估服务质量方面的局限性,该方案应用有效带宽与有效容量概念从链路层对源数据模式与队列服务动态进行统计特性建模.该链路层模型分别描述了源数据产生过程、信道服务过程与服务质量参数之间的映射关系,将超时违约概率约束转化为数据传输速率限制,将帧长优化问题转换为求解多元联合不等式组.在块衰落信道场景中,求解满足多元联合方程的帧长域下界,得到超时违约概率约束下的最佳系统帧长.理论分析和仿真结果表明,在最佳帧长设置下,用户数据传输的超时违约概率满足要求.

超时违约概率;帧长优化;有效带宽;有效容量;多天线系统;服务质量

TN92

Foundation items：The National Science and Technology Major Project (No.2012ZX03004005-003), the National Natural Science Foundation of China (No.61171081, 61201175), the Research Fund of National Mobile Communications Research Laboratory of Southeast University (No.2014A03).

：Tan Yufeng, Li Junchao, Xia Weiwei, et al.Frame length optimization for multi-antenna downlink systems based on delay-bound violation probability constraints[J].Journal of Southeast University (English Edition),2015,31(2):163-169.

10.3969/j.issn.1003-7985.2015.02.001

10.3969/j.issn.1003-7985.2015.02.001

Received 2014-11-04.

Biographies：Tan Yufeng (1988—), female, graduate; Shen Lianfeng (corresponding author), male, professor, lfshen@seu.edu.cn.