一种基于优化融合算法的机器人路径规划技术

刘传领, 韩承雪

一种基于优化融合算法的机器人路径规划技术

刘传领1, 韩承雪2

(1.商丘师范学院 计算机与信息技术学院,河南 商丘 476000； 2. 商丘职业技术学院,河南 商丘 476100)

局部最优问题是当前移动机器人路径规划算法中存在的一个关键问题. 为了解决该问题，文章提出了一种基于PSO和QGA的移动机器人路径规划算法. 该算法利用粒子群具有记忆能力、能参考局部最佳位置方向和全局最佳位置方向进行择优搜索的特点，对路径进行局部优化；然后利用量子遗传算法的收敛速度快和全局寻优能力强的特点，对最优或次优个体进行选择, 为最优或次优个体进入下一代提供了保障，提高了算法的性能. 仿真结果表明，该算法的稳定性及寻优能力均被明显改善，且有更好的收敛性以及更强的连续空间搜索能力，适合于求解复杂优化问题.

粒子群优化；路径规划；移动机器人；量子遗传算法

移动机器人路径规划是机器人领域的一项重要课题，机器人根据自身传感器对环境的感知，从起始点到目标点之间找到一条安全无碰的路径,高效完成作业任务. 依据对环境知识的了解,可分为已知环境、部分已知环境和未知环境下的路径规划[1]78，[2]279，[3]476. 智能移动机器人路径规划的研究起始于20世纪70年代，许多学者对其进行了深入地研究，取得了大量的研究成果，且已进入了政府和商业的实际应用领域[4]110，[5]1646，[6]903，[7]1356，[8]134. 2008年徐玉如等提出了一种基于遗传算法和粒子群优化算法的全局路径规划思想[5]1647，用于水下机器人导航. Casillas等人[6]907提出了一种基于模糊系统不确性的多目标遗传数据挖掘算法，该方法采用模糊规则和多目标遗传的融合算法应用于客户的行为消费模型，有效处理了客户消费行为中的许多不确定性数据. Kumar和Rao结合蚁群算法和遗传算法及基于数据挖掘的技巧，提出了一种新的混合遗传算法并应用于工作调度等问题，也取得了较好的效果[9]589，[10]39-43. 但这些算法在应用中也存在不足，例如，出现局部最小问题、运行时间长、找不到最优解等.

基于以上分析，本文提出了一种基于PSO和QGA的移动机器人路径规划技术. 该算法在量子遗传算法中融合粒子群优化算法的优点实现一种混合路径规划技术，通过粒子群优化方法来实现量子比特状态的更新,实现了对空间广泛细致的搜索. 通过仿真实验证明该算法具有更快的收敛速度和很好的实用性.

1 PSO及其改进

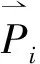
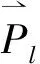
这里c1、c2被称为学习因子，根据实际情况取值，rand1()、rand2()是均匀随机函数.vij(t-1)反映了个体的运动“习惯” ，即个体具有保持自己原先运动状态的趋势；c1rand1()(Pij-xij(t-1))反映了个体对自己原先运动状态的记忆或回忆，说明个体具有向自己最佳位置逼近的趋势；c2rand2()(Plj-xij(t-1))反映了个体之间协同合作，代表个体具有向群体或邻域最佳位置逼近的趋势[11]69-73. 为了迅速找到最优解，本文对粒子群优化算法做如下改进：

1)动态探测机制的引入，使粒子个体获得能够感知环境变化的能力；

2)环境响应机制的引入，在探测到环境变化后，采用相应的响应措施来适应环境的变化.

具体的设计方案为：

1)利用探测粒子探测环境是否发生变化，若没有变化，则不改变算法；

2)若环境发生改变，把改变的环境空间划分为N1个均匀的子空间；在每个子空间内随机设置N2个敏感粒子；

3)计算每次迭代时敏感粒子适应值fi，并计算相邻2次迭代适应值的差值Δfi；

Δfi=f(i+1)-f(i) (1in)

4)对所有差值的绝对值求和F.

×

当F=0，环境不发生变化；F>0，环境发生变化，则设置响应阈值Fthreshold，当F>Fthreshold时，对粒子的位置和速度进行修改.

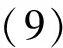
vi(t)=(vi1,vi2,…,

2 QGA及PSO和QGA的融合方法

2.1 量子比特编码

一个量子比特的状态可以取0或1，其状态表示为

|φ〉=α|0〉+β|

其中α、β为代表相应状态出现概率的两个复数，且

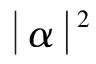
对一个具有s位量子态的数据q，构造对应数据结构p，p为长度为s的二进制串，p称为观测态[12].q和p分别为：

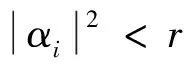
2.2 量子染色体变异操作

量子染色体变异是通过量子态的变换来实现的，即通过量子门的旋转角变换来实现量子染色体的变异操作, 加快收敛速度. 量子旋转门的调整操作如下:

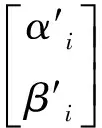
θi=s(αi,βi)Δ

θi=s(αi,βi)和Δθi分别代表量子门旋转的方向和角度,根据经验Δθi的取值一般在0.1π～0.005π之间.

2.3PSO和QGA的融合流程

PSO-QGA算法流程描述如下：

Step1 算法初始化，t=t+1；

Step3 染色体变异：根据变异概率，对染色体的量子比特的几率幅(α,β)位置对调；

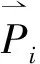
Step5 根据2.1节的粒子群优化算法进行局部优化和确定全局优化解；

Step6 判断是否满足终止条件，若满足则退出；否则t=t+1，转到step3，进入循环迭代.

3 仿真结果与分析

采用Matlab仿真软件，对上述算法进行了仿真测试. 为了便于测试，仿真试验放在10×10和20×20单位区域的环境中进行，机器人起点(Start)设在(0，0)点，目标点(End)设在(9，9)点. 算法参数为：群体规模为n=30，个体长度m=40，迭代次数t=60，学习因子c1=1.5，c2=2.0，vmax=10.

实验1 如图1所示，S点为机器人的出发点，E为机器人的终点，实验在10×10单位区域环境中进行. 实验分别给出了PSO算法、QGA算法和本文算法规划的路径，结果显示，PSO算法规划的路径是一条无效路径，QGA算法规划的路径是一条非优化路径，本文算法规划的路径是一条优化路径 . 如图2所示给出了本文算法在20×20单位区域环境中的实验，规划出了一条优化路径.

实验2 因为路径规划是在满足安全的条件下寻找一条耗时最少、距离最短的优化路径，因此，如图3所示中路径的适应值越小，则路径越优化. 图3给出种群平均适应值及最优个体的进化图，结果显示，对于个体最优来说，算法运行到18次时就基本达到最优，而对于种群的平均优化来说，算法运行到43次时才能到达基本最优. 因此，在进化过程中应该根据实际情况选择最优解进入下一代.

图1 三种算法性能的比较

图2 本文算法规划的优化路径

图3 本文算法进化图

实验3 在相同实验条件下，对遗传算法(GeneticAlgorithm，GA)、QGA算法和本文算法从可行解平均长度、获得可行解比例、平均消耗时间进行了性能比较. 实验结果表明本文算法的优化能力比较强. 见表1.

表1 三种算法的测试数据

4 结论

粒子群优化算法和量子遗传算法都是应用比较广泛的优化算法，应用于移动机器人路径规划取得了良好的效果. 本文算法融合了两种算法的优点，通过粒子群优化来实现量子比特状态的更新，从而更加方便、简洁. 此算法应用于机器人路径规划技术上，表现出了比较稳定的性能、较快的寻优速度. 仿真实验结果表明，本文所提算法在稳定性能、寻优能力和收敛性方面均优于PSO算法、GA算法和QGA算法.

[1] 刘传领，杨静宇. 复杂环境下解决势场法局部极小问题的路径规划方法[J].哈尔滨理工大学学报, 2014，31(11).

[2]XU,C.MING,A.NAGAOKA,T.SHIMOJO,M..Motioncontrolofagolfswingrobot[J].InJournalofRoboticandSystem,February2009,Vol.56.

[3] 李 磊, 叶 涛, 谭 民, 等. 移动机器人技术研究现状与未来[J]. 机器人,2002, 24(5).

[4] 徐玉如, 姚耀中. 考虑海流影响的水下机器人全局路径规划研究[J]. 中国造船, 2008, 49(4).

[5]CasillasJ，etal.Mininguncertaindatawithmultiobjectivegeneticfuzzysystemstobeappliedinconsumerbehaviormodeling[J].ExpertSystemswithApplication, 2009, 36(2).

[6]KumarS，RaoCSP.Applicationofantcolony,geneticalgorithmanddatamining-basedtechniquesforscheduling[J].RoboticsandComputer-IntegratedManufacturing, 2009, 25(6).

[7]HanKuk-Hyun,KimJong-Hwan.Geneticquantumalgorithmanditsapplicationtocombinatorialoptimizationproblem[C].Proceedingsofthe2000CongressonEvolutionaryComputation, 2000.

[8] 朱庆保, 张玉兰. 基于栅格法的机器人路径规划蚁群算法[J]. 机器人，2005，27(2).

[9] 朱庆保. 复杂环境下的机器人路径规划蚂蚁算法[J]. 自动化学报, 2006, 32(6).

[10]EberhartR,KennedyJ.Anewoptimizerusingparticlewarmtheory[A].ProccedingsoftheSixthInternationalSymposiumonMicroMachineandHumanScience[C].Nagoya:IEEEPress, 1995.

[11]ShiY,EberhartRC.Amodifiedparticleswarmoptimizer[C].ProceedingsofInternationalConferenceonEvolutionComputationAnchorage, 1998.

[12]knightP.Quantuminformationprocessingwithoutentanglement[J].Science, 2000(287).

[责任编辑 冰 竹]

A Mobile Robot Path Planning Technology Based on Optimization Fusion Algorithm

LIU Chuanling1, HAN Chengxue2

(1.DepartmentofComputerandInformationTechnology,ShangqiuNormalUniversity,Shangqiu476000,China;2.ShangqiuVocationalandTechnicalCollege,Shangqiu476100,China)

Local optimum is a key problem in current research related mobile robot path planning methods. In order to solve the problem, a novel mobile robot path planning algorithm is proposed in this paper, which uses memory ability, the ability of the best position & direction investigation of the individual and the global of particle swarm optimization (PSO) to plan path locally for mobile robot, and uses fast convergence & searching the best solution capability of quantum genetic algorithm (QGA) to select the optimal or sub-optimal path in order to protect the optimal or sub-optimal path into the next generation. It increases greatly the efficiency of the algorithm. Results of the simulation demonstrate the ability of finding the best solution and the stability of this method are greatly improved, it has better convergent property and ability of searching more extensive space and is fit for finding the solution in complex optimization problems.

particle swarm optimization (PSO); path planning; mobile robot; quantum genetic algorithm (QGA)

2015-01-28

刘传领(1969- )，男，河南商丘人，商丘师范学院副教授，博士，主要从事为模式识别、计算机智能控制研究。

1671-8127(2015)02-0012-04

TP202.7

A