最大传输功率之再探究
崔克楠,陶源盛
(电子科技大学 光电信息学院, 成都 611731)
最大传输功率之再探究
崔克楠,陶源盛
(电子科技大学 光电信息学院, 成都 611731)
在信号传输时,功率是考虑的重要因素之一。在教材中最大功率传输定理的基础上,对正弦稳态下的最大传输功率做了更深入的讨论,得出了戴维南阻抗和负载在三种特殊限制条件下的最大传输功率。介绍了在负载不能任意改变的情况下,为实现最大功率传输而通常选用的三种LC匹配网络:“L”型匹配网络、“T”型匹配网络和“π”型匹配网络,并经讨论得出三种匹配网络本质上是一种网络,即“L”型匹配网络。
最大传输功率;戴维南阻抗;LC匹配网络
在分析从电源到负载的功率传输的设计方案时,最大传输功率往往是关注的核心之一。因为通信系统和测量系统的信号源的输出功率有限,因此希望在信息或数据的传输中要求负载能达到最大传输功率。
文献[1-2]给出的最大功率传输定理仅适用于纯电阻电路、共轭匹配、模匹配等三种情况的计算。
本文将对正弦稳态系统的最大传输功率做更进一步的探讨。首先,推导戴维南阻抗与负载在受限制情况下的最大传输功率;然后,推导在不改变负载的情况下,如何通过添加匹配网络使负载达到最大传输功率。
1 电路受限制
以往的文献中,已经对纯电阻电路中的最大功率传输定理和电抗电路中共轭匹配、模匹配有了详细的推导,故在此不再赘述。本文将详细地推导在电路受限制[3]的三种情况下的最大传输功率。
由戴维南定理可知,任何一个线性电阻单口网络,就端口特性而言,都可以等效为戴维南电路。因此,工程上常把负载阻抗Z0=R0+jX0以外的线性网络等效为电压源U0和戴维南阻抗Z0=R0+jX0串联的戴维南等效电路,如图1所示。

图1 戴维南等效电路图
1.1 戴维南阻抗为感性,负载阻抗为感性
在戴维南阻抗为感性,负载阻抗为感性时,即满足这样的条件:
(1)
则电流和功率可表示为:
(2)
对P求关于PL和XL的偏导数可得:
(3)
由于XL>0,X0>0条件限制,无法满足下面的条件:
(4)
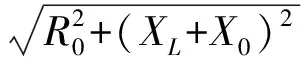
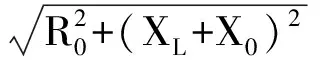
而当戴维南阻抗为容性,负载阻抗为容性时,若要达到最大传输功率,也是同样的道理。
1.2 戴维南阻抗为纯电容或纯电感
在戴维南阻抗为纯电容或纯电感,即满足这样的条件:
(5)
则电流和功率可表示为:
(6)
对P求关于PL和XL的偏导数可得:
(7)
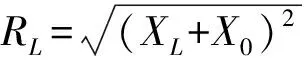
当XL=-X0,RL越趋近于零,负载所得到的传输功率便越大。
故此类也是一种极限问题。在此种情况下,负载的传输功率没有最大值。只有当XL=-X0,RL越趋近于零,负载获得的传输功率越大。
1.3 负载为纯电容或纯电感
当负载为纯电容或纯电感时,满足以下条件:
(8)
(9)
由式(9)可见,当负载为纯电感或纯电容时,负载的传输功率一定为零。
在通信和电子设备的设计中,常常需要满足共轭匹配或模匹配,以便使负载获得最大传输功率。那么在负载不能任意变化的情况下,应该怎样才能提高负载所获得的传输功率呢?
2 匹配网络
在含源单口网络与负载之间插入一个由异性电抗元件构成的“阻抗变换电路即匹配网络”[5],可以满足负载获得最大传输功率的条件。下面介绍4种常用的LC匹配网络。
2.1 “L”型匹配网络
在纯电阻电路中,通常选用“L”型匹配网络来实现最大功率传输。
根据R0与RL的大小关系分为两种情况讨论。
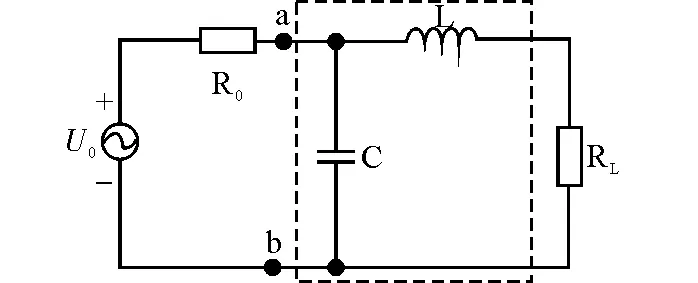
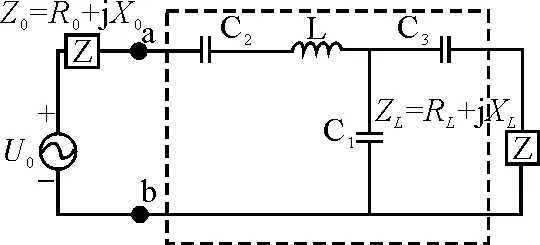
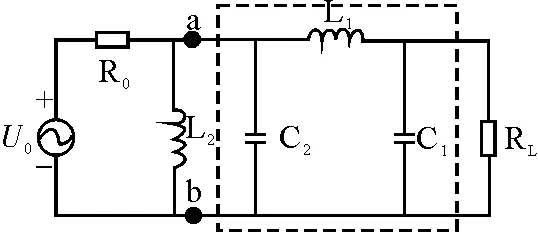
1)R0 在这种情况下常用转置“L”型匹配网络[6]。该匹配网络由适当规格的电感元件与电容元件组成,电路如图2所示,虚线框内为转置“L”型匹配网络。 图2 R0 为了计算方便,将电容与电阻的并联单口等效转换为串联单口,再写出由LC匹配网络和负载电阻共同形成的单口网络ab端的输入阻抗,并令它等于戴维南阻抗的共轭复数[7]。 电感与电容元件的具体数值推导如下: R0-jX (10) 令式(10)的实部等于R,其虚部为零可得: (11) (12) 2)R0>RL 在这种情况下选用倒“L”型匹配网络,仍由适当规格的电感与电容元件组成,电路如图3所示,虚线框内即为倒“L”型匹配网络。 图3 R0>RL的“L”型匹配网络图 电感与电容的数值推导过程与2.1类似,此处不再赘述,直接给出L与C的计算公式: (13) 2.2 “T”型匹配网络 在纯电阻电路中可采用“L”型匹配网络,在电抗电路中,通常采用“T”型匹配网络来实现最大功率传输[8]。 例如:戴维南阻抗与负载阻抗分别为Z0=R0+jX0,ZL=RL+jXL,且X0,XL>0,即戴维南阻抗与负载阻抗均为感性,要实现最大功率传输,可以设计一个“T”型匹配网络。电路如图4所示,虚线框内为“T”型匹配网络。 图4 “T”型匹配网络图 匹配网络中的两个电容元件C2、C3分别抵消了戴维南阻抗、负载上的电感分量X0、XL。完全抵消后的电路可以等效为2.1中图1的情形,即可看作纯电阻电路。接着按照2.1中的设计方法选取适当规格的电感与电容元件构成“L”型网络就可以实现最大功率传输。 电容C2、C3抵消电感分量X0、XL,故有: (14) (15) 电感L与电容C的具体数值可以利用式(11)与式(12)进行计算 2.3 “π”型网络 在电抗电路中,也可以选用“π”型匹配网络实现最大功率传输[9]。 例如:戴维南阻抗为纯电阻R0与电感L2并联,负载为纯电阻RL,我们就可利用“π”型匹配网络来实现最大功率传输。电路如图5所示,虚线框内为“π”型匹配网络。 图5 “π”型匹配网络图 电容C2的作用是完全抵消电感L2在电路中所起的影响,这时的电路就可以等效为2.1节中图1所示的情形。匹配网络余下的L1、C1构成“L”型网络并实现最大功率传输。 电容C2完全抵消电感L2在电路中所起的影响,故有 (16) 解得 (17) L1、C1的数值同样可以利用式(11)与式(12)计算,此处不再赘述。 2.4 “L”型、“T”型、“π”型匹配网络的一致性 “L”型、“T”型、“π”型三种匹配网络的形式虽然不同,但本质是相同的。 “T”型、“π”型匹配网络都是在“L”型网络的基础上改进而来的。当电路为纯电阻电路且戴维南等效电阻与负载不相等时,根据两者的大小关系分别选用两种“L”型匹配网络。 当电路为电抗电路,根据电路的实际情况,只需在“L”型网络基础上添加相应的电抗元件抵消掉戴维南阻抗与负载的电抗分量即可,增加的电抗元件和原有“L”型网络就构成了“T”或者“π”型网络型匹配网络。 由此可见,三种网络本质上是一种网络,即“L”型匹配网络。 本文从教材中已给出的纯电阻电路最大功率传输定理和共轭匹配、模匹配出发,对电路在限制条件下达到最大传输功率做了更为深入的讨论,从数学的角度推导出了戴维南阻抗为感性且负载阻抗为感性、戴维南阻抗为纯电容或纯电感、负载为纯电容或纯电感等三种特殊情况时的最大传输功率。当戴维南阻抗和负载阻抗不能任意改变时,根据电路的实际情况,通过设计添加“L”型、“T”型、“π”型三种匹配网络,使负载获得最大传输功率,并分别通过推导说明如何添加电抗元件来构成匹配网络。 [1]胡翔骏.电路分析[M].2版.北京:高等教育出版社,2007. [2]张伟,张蛟龙,韩素敏.重视电路中最大功率传输定理的使用条件[J].中国电子教育,2009(3):55-57. [3]左全生.负载阻抗受限制情况下的最大功率传输的研究[J].常州工学报,2008,21(2):32-34. [4]傅英定.微积分(下册)[M].2版.北京:高等教育出版社,2009:11-14,66-67. [5]拉巴次仁.正弦稳态电路中负载获得最大平均功率情况分析[J].西藏大学学报,2012,27(1):107-110. [6]鲁业频.基于匹配网络若干问题的推论[J].大学物理,1997,16(7):11-12. [7] 胡翔骏.电路分析[M].2版.北京:高等教育出版社,2007:411-412. [8] 刘秀成,黄松岭,于歆杰,等.关于最大功率传输问题的讨论[J].电气电子教学学报,2008,30(1):19-22. [9] 刘岚,聂丹.分立元件的匹配网络设计与仿真[J].信息技术,2004,28(4):58-60. Reconsideration of Maximum Power Transfer Law CUI Ke’nan, TAO Yuansheng (School of Optoelectornic Information, University of Electronic Science and Technology of China, Chengdu 611731, China) In the signal transmission, power is one of the most important factors to be considered. The first part of the paper discusses on sinusoidal steady-state maximum power transmission on the basis of the maximum power transfer theorem, and works out the maximum power transfer of Thevenin’s equivalent resistance under three specific boundary conditions. The second part of the paper introduces three typical LC matching networks used to achieve maximum power transfer under the circumstances in which the load cannot be changed arbitrarily: the “L” matching network, the “T” matching network and “π” matching network, and discuss the three matching networks are essentially a network that is “L” matching network. maximum power transfer; Thevenin impedance; LC matching network 2014-07-16;修改日期: 2014-09-08 崔克楠(1995-),男,本科在读,专业方向:光电信息显示专业。 TM131 B 10.3969/j.issn.1672-4550.2015.04.068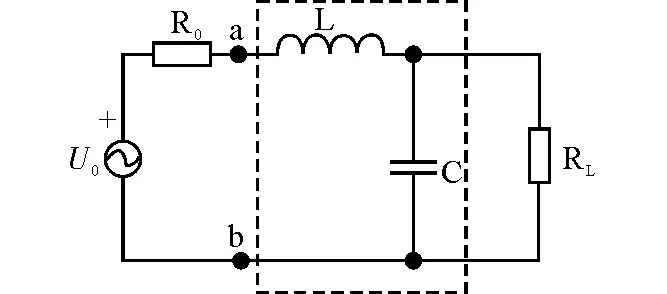
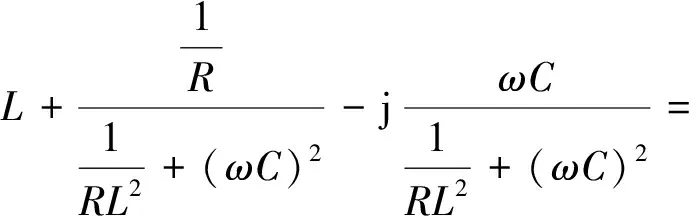
3 结束语

