基于AIUKF的WSN节点定位算法*

欧县华,武宪青,何熊熊

(浙江工业大学信息工程学院,杭州 310023)



基于AIUKF的WSN节点定位算法*

欧县华,武宪青,何熊熊*

(浙江工业大学信息工程学院,杭州 310023)

针对无线传感器网络节点定位精度不足的问题,在无迹卡尔曼滤波(UKF)的基础上,结合迭代约束条件和自适应因子,提出了一种自适应迭代无迹卡尔曼滤波(AIUKF)算法。根据基于测距的节点定位模型,采用RSSI进行测距,以极大似然估计法进行节点初步定位,利用AIUKF算法对节点进行精确定位,并且直接以RSSI作为系统的观测量。仿真结果表明,本文提出的基于AIUKF的定位算法相比EKF和UKF算法具有更高的定位精度。

无线传感器网络;节点定位;AIUKF;UKF;自适应因子

无线传感器网络作为一个新型的网络,现已被广泛应用于国防军事、环境监测、医疗看护等诸多领域,被认为是21世纪影响人类生活的21项技术之一。在无线传感器网络的相关研究与应用中,节点定位技术不仅是研究中基础和热点问题,也是决定应用有效性的关键技术之一[1-2]。

无线传感器网络节点定位算法常见的分类是基于测距的定位算法(Range-Based)和无需测距的定位算法(Range-Free)[3]。前者根据信标节点位置信息以及未知节点与信标节点之间的距离或角度信息来实现对未知节点的定位,常用的测距方法有[4]:TOA、TDOA、AOA、RSSI;后者仅根据网络的连通度来确定未知节点的位置信息。

鉴于基本算法实现的定位精度有限,国内外许多学者将滤波技术应用到WSN节点定位中,取得了大量的研究成果。对于非线性系统,最常用的是扩展卡尔曼滤波(EKF)算法[5]。文献[6]首次将扩展卡尔曼滤波技术应用于节点定位修正阶段中,相比基本的定位算法,定位精度有了较大程度的提高。然而,EKF使用泰勒展开式近似代替非线性系统时,往往忽略一阶以上的高阶项,在计算过程中可能会引入较大的误差,造成估计精度的降低,严重时会引起滤波器发散;同时,标准EKF及其衍生算法都需要计算雅可比矩阵,这个在许多实际问题中可能很难甚至无法求得。为避免上述问题,Julier等人提出了基于无迹变换的无迹卡尔曼滤波(UKF)算法[7-8],相比EKF,UKF无需计算雅可比矩阵,且对任意系统,利用无迹变换得到的近似状态的均值和方差可以精确到二阶或更高阶,具有更高的估计精度。文献[9]将加权最小二乘估计和UKF用于WSN节点定位中,取得了比EKF更好的定位性能。但是UKF仍存在对初始值的波动以及观测噪声比较敏感等问题,初始值的波动会造成UKF的估计结果不稳定,精度变差。为此,文献[10]提出迭代无迹卡尔曼滤波算法(IUKF),改善了UKF算法存在的一些问题,应用到WSN定位中得到了较好定位性能,但是,数值稳定性等问题仍然存在,为了改善上述问题,本文在IUKF算法的基础上,结合自适应抗差滤波理论[11-12]提出一种自适应迭代UKF算法,提高定位精度,增强算法的稳定性。

1 节点初始定位

1.1 RSSI测距模型

在基于RSSI的节点定位算法中,测距是节点定位算法的基础。RSSI测距是根据已知的未知节点发射信号强度和信标节点接收到的信号强度,得到能量损耗值,并使用理论或经验模型将其转化为距离值。在实际应用中,最常用的理论测距模型是对数-常态分布模型[13]。

Pr(dr)=Pr(d0)-10·δ·log(dr/d0)+χσ

(1)

式中,Pr(dr)为经过距离dr后的信号接收能量值;d0为参考距离,一般取1 m;Pr(d0)为经过距离d0后的信号接收能量值;δ为路径损耗因子,与信号传输环境相关;χσ为均值等于0的高斯随机变量。

1.2 节点初始定位

在基于测距的定位算法中,常见的基本定位方法有三边测量法、三角测量法和极大似然估计法。当信标节点的数目较小时,三边测量法的定位精度较高,但当信标节点数目超过6个时,极大似然估计法的精度更高[14]。本文采用极大似然估计法作为初始定位方法。

设(x1,y1)、(x2,y2)、…、(xn,yn)表示n个位置信息已知的信标节点的坐标,每个信标节点与未知节点之间的距离对应为d1、d2、…、dn,根据极大似然估计法的原理使用MMSE法求得未知节点初始定位坐标(xMLE,yMLE)为:

(2)

式中,X=[xy]T,

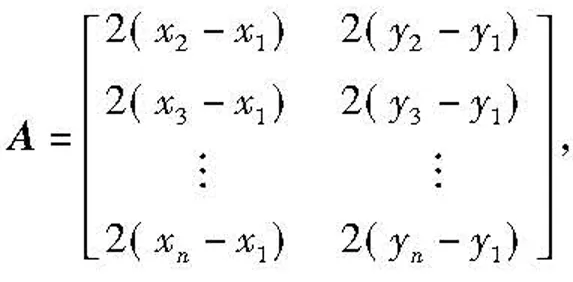
2 自适应迭代UKF算法

2.1 定位算法模型

在引入卡尔曼滤波技术估计的WSN节点定位算法模型中,离散时间非线性系统的一般形式为:

(3)

式中,X为系统状态向量;Y为系统的观测量;uk-1为确定控制项;wk和vk分别为系统的过程噪声和观测噪声,其协方差矩阵分别为Qk和Rk。

将未知节点的坐标作为系统的状态量,而关于观测量的选取,文献[9]将未知节点与信标节点之间的距离值作为系统的观测量,但是需要求解雅可比矩阵,并有可能造成距离计算过程中的误差累积,故在本文中,直接采用RSSI值作为观测量。因此,引入卡尔曼滤波的WSN节点定位算法中的状态方程和观测方程为:

①状态方程:

Xk+1=f(Xk,uk-1)+wk=AXk+wk

(4)

式中,Xk=[xk,yk]T表示未知节点在第k时刻滤波计算的状态向量;A为状态转移矩阵,由于实现的是静态节点定位,故A为单位矩阵。

②观测方程

(5)

2.2 标准UKF算法实现:

标准UKF算法流程如下:

①初始化:

(6)

②样点计算:

(7)

式中:λ=α2(L-κ)-L;α决定样点的散布程度,取值范围为10-4≤α≤1,一般取0.01;L为系统状态变量X的维数;κ为调整参数,一般取0。

③时间更新:

(8)

(9)

(10)

(11)

(12)

(4)量测更新:

(13)

(14)

(15)

(16)

(17)

2.3 迭代策略与自适应因子的选取

虽然UKF算法对EKF算法存在的一些问题有了明显的改善,但是UKF算法的基础也是卡尔曼滤波,因此,其仍存在着受初始值波动、可观测性弱、观测噪声不确定性等因素影响而造成滤波精度和鲁棒性降低等问题。在基于RSSI的WSN节点定位中,RSSI易受各种干扰因素影响使其值具有较大的误差,同时造成测距阶段可能产生较大误差而使得采用MLE法获得的结果具有较大的波动性,这些因素都会造成基于UKF的定位算法的性能变差。为改善上述问题,本文在标准UKF算法的基础上,结合文献[10]提出的迭代策略,同时引入自适应因子,以抑制初始值波动和观测量异常值等因素的影响,提高定位算法定位精度和稳定性。

①迭代策略

文献[10]提出的IUKF算法迭代策略的判断准则如下:

(18)

②自适应因子δk的选取

确定自适应因子常用的几种误差判别统计量分别是状态不符值统计量、预测残差统计量和方差分量比统计量[11]。由于本文采用RSSI作为观测量是已知的,且使用预测残差向量能较好的反应系统中的异常扰动,也无需在滤波前计算状态向量参考值,故采用预测残差统计量作为判别统计量,参照两段式函数提出的自适应因子定义如下:

(19)

将标准UKF方程中的式(10)、式(13)～式(17)更新为下面的式(20)～式(24),即可得到自适应迭代UKF算法方程。

(20)

(21)

(22)

(23)

(24)

式中,g=ηg,η为衰减因子,其取值范围为:0<η<1。

2.4 基于AIUKF的节点定位算法流程

Step 1:使用极大似然估计(MLE)法求得节点初始定位坐标值(xMLE,yMLE)。

Step 3:计算并更新自适应因子δk。

3 算法仿真与分析

利用MATLAB对本文提出的定位算法进行仿真分析,并与相关方法进行对比,验证该算法的性能。仿真区域设置为30 m×20 m,根据式(1)生成RSSI数据,并在数据中添加零均值的高斯白噪声,来代替实际环境中的多种干扰因素的影响。分别考虑两种仿真场景:①利用3个信标节点对单一未知节点进行定位;②未知节点数目与位置固定,改变信标节点的数目,对未知节点进行定位。

3.1 仿真场景1

仿真中的参数初始化设置如下:系统噪声协方差矩阵Q=diag([0.2,0.2]),观测噪声协方差矩阵R=diag([0.25,0.25,0.25]),UKF算法中的参数α=0.01,β=2,κ=0,初始状态误差协方差矩阵P0=diag([0.001,0.001])。AIUKF算法中的最大迭代次数限制设置并不需要过大,在仿真中设为3次。

仿真中三信标节点的坐标为:(26,0),(14,20),(0,10),未知节点的真实位置为(14,12)。针对基于EKF,UKF,AIUKF的3种定位算法独立仿真100次,该仿真情形中采用节点定位误差和平均定位误差来衡量算法的性能。

(25)

式中,(x,y)表示未知节点的真实坐标值,(xi,yi)表示第i次迭代获得的未知节点坐标值。

(25)

式中:M代表仿真的次数。

假定定位误差ε<1.2·εm视为收敛,3种定位算法的节点定位误差的数据统计特性如表1所示。

表1 定位误差数据统计表

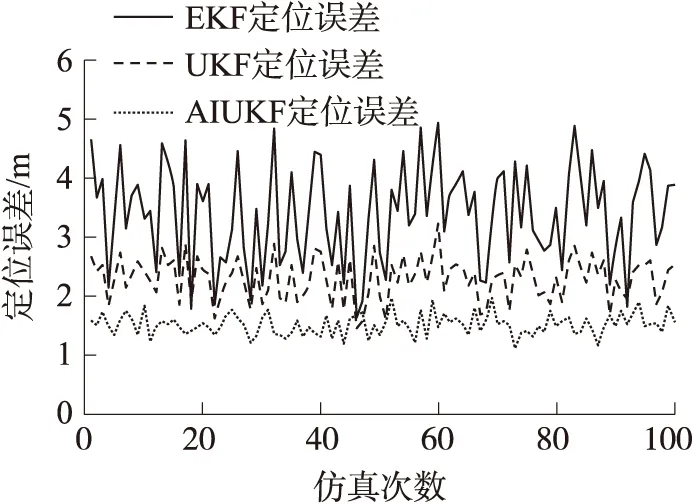
图1 3种算法下的定位误差曲线对比图

仿真的定位误差对比曲线图如图1所示。

从图1中可以看出,基于AIUKF的定位算法相比UKF算法和IUKF算法不仅在精度上有了明显的提高,并且呈现较好的收敛性。由表1可知,基于EKF、UKF和AIUKF的3种算法的平均定位误差分别为:3.399 3m,2.289 3m,1.512 6m。AIUKF算法较EKF和UKF算法其定位精度分别提高55.5%,33.9%。同时AIUKF算法精度的波动范围仅为EKF算法的25.7%,UKF算法的48%。因此,在相同的条件下,基于AIUKF的定位算法具有更高的定位精度和较好的收敛性。

3.2 仿真场景2

为了进一步对比验证3种定位算法的性能,固定未知节点位置,信标节点的数量从3个依次增加到9个,进行仿真,采用平均定位误差来衡量3种定位算法的性能。不同信标节点数目下3种算法的平均定位误差对比曲线图如图2所示。

图2 不同信标节点数下平均误差对比曲线图

从图2中可以看出,3种算法中,AIUKF算法的平均定位误差最低。3个信标节点时,EKF、UKF、AIUKF算法的平均定位误差分别为:3.399 3m、2.289 3m、1.512 6m,9个信标节点时,三算法的平均定位误差分别为1.613 2m、0.753 9m、0.437 7m。AIUKF算法相对EKF算法精度分别提高了55.5%和72.87%,相对UKF算法分别提高了33.93%和72.24%。同时,平均定位误差随着信标节点数目的增加定位误差逐渐降低,但当信标节点数目达到一定数目后,变化趋于平缓。因此,在应用中,在一定范围内增加信标节点数目可提高定位精度,但无限增加信标节点的数目却无助于提高定位精度,反而会增加算法的复杂度和成本,没有实际意义。

4 结论

本文在标准UKF的基础上,结合迭代UKF和自适应抗差滤波理论,提出了一种基于AIUKF的WSN节点定位算法。采用极大似然估计法进行初始定位,作为AIUKF算法的初始值,并且直接以信标节点接收到的信号能量值作为观测方程的观测量。仿真结果表明,在固定未知节点和增加信标节点数目的情况下,本文的算法不仅在定位精度,而且在稳定性方面都明显优于其他算法,具有很高的应用价值。

[1] Chong C Y,Kumar S P.Sensor Networks:Evolution,Opportunities,and Challenges[J].Proceedings of the IEEE,2003,91(8):1247-1256.

[2]陈锡剑,程良伦.基于RSSI的功率匹配定位算法的研究与实现[J].传感技术学报,2013,26(5):709-714.

[3]Bal M,Liu M,Shen W,et al.Localization in Cooperative Wireless Sensor Networks:A Review[C]//Proceedings of 19th International Conference on Computer Supported Cooperative Work in Design,2009:438-443.

[4]Blumrosen G,Hod B,Anker T,et al.Enhancing RSSI-Based Tracking Accuracy in Wireless Sensor Networks[J].ACM Transactions on Sensor Networks,2013,9(3):29.

[5]Jiang Z,Song Q,He Y,et al.A Novel Adaptive Unscented Kalman Filter for Nonlinear Estimation[C]//Proceeding of 46th IEEE Conference on Decision and Control:IEEE,2007:4293-4298.

[6]Savvides A,Park H,Srivastava M B.The Bits and Flops of the N-hop Multilateration Primitive for Node Localization Problems[C]//Proceedings of the 1st ACM International Workshop on Wireless Sensor Networks and Applications:ACM,2002:112-121.

[7]Julier S J,Uhlmann J K,Durrant H F.A New Approach for Filtering Nonlinear Systems[C]//Proceedings of the 1995 American Control Conference,IEEE,1995,3:1628-1632.

[8]Julier S J,Uhlmann J K,Durrant H F.A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators[J].IEEE Transactions on Automatic Control,2000,45(3):477-482.

[9]梁玉琴,曾庆华,刘建业.基于UKF滤波的WSN节点定位研究[J].传感技术学报,2010,23(6):878-882.

[10]Zhan R,Wan J.Iterated Unscented Kalman Filter for Passive Target Tracking[J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(3):1155-1163.

[11]杨元喜,任夏,许艳.自适应抗差滤波理论及应用的要进展[J].导航定位学报,2013,1(1):9-15.

[12]高为广,何海波,陈金平.自适应UKF算法及其在GPS/INS组合导航中的应用[J].北京理工大学学报,2008,28(6):505-509.

[13]袁鑫,吴晓平,王国英.线性最小二乘法的RSSI定位精确计算方法[J].传感技术学报,2014,27(10):1412-1417.

[14]彭宇,王丹.无线传感器网络定位技术综述[J].电子测量与仪器学报,2011,25(5):389-399.

Adaptive Iterated UKF Based Node Localization for WSN*

OUXianhua,WUXianqing,HEXiongxiong*

(College of Information Engineering,Zhejiang University of Technology,Hangzhou 310023,China)

In this paper,by combining iterative constraint conditions and adaptive factor,an adaptive iterated unscented Kalman filter(AIUKF)algorithm is presented to improve the node localization accuracy in Wireless Sensor Network(WSN),which is based on the unscented Kalman filter(UKF).According to the model of range-based localization algorithm,RSSI is used to measure the distance;the maximum likelihood estimation method is utilized to realize node initial location;by using AIUKF algorithm to achieve the accurate positioning of the node finally and RSSI is applied as the measurement values of observation equation directly.The simulation results show that the proposed algorithm based on AIUKF has the best positioning precision than EKF algorithm and UKF algorithm.

WSN;node localization;AIUKF;UKF;adaptive factor

欧县华(1990-),男,硕士研究生,主要研究方向为无线传感器网络节点定位算法,oxhzjut@163.com;

武宪青(1987-),男,博士研究生,主要研究方向为欠驱动桥式吊车系统控制、TORA系统控制,wux.zjut@gmail.com。

何熊熊(1965-),男,教授,博士生导师,主要从事迭代学习控制、信号处理等方面的研究,hxx@zjut.edu.cn;

项目来源:“十二五”国家科技支撑计划项目(2013BAF07B03);国家自然科学基金项目(61473262);浙江省重大科技专项项目(2011C13011)

2014-10-30 修改日期:2014-11-29

C:6140B;6150P;7230

10.3969/j.issn.1004-1699.2015.02.015

TP393

A

1004-1699(2015)02-0234-05