基于集中质量法的深水S型铺管动力响应研究
孙丽萍, 宋环峰, 艾尚茂
(1. 哈尔滨工程大学,哈尔滨 150001; 2.中国船舶科学研究中心上海分部,上海 200011)
基于集中质量法的深水S型铺管动力响应研究
孙丽萍1, 宋环峰2, 艾尚茂1
(1. 哈尔滨工程大学,哈尔滨 150001; 2.中国船舶科学研究中心上海分部,上海 200011)
深水S型铺设时,管线承受巨大的环境载荷,需要准确地模拟管线受力,以保证管线安全。基于集中质量法,推导管线受力计算公式,建立考虑海床、托管架以及海流影响的S型铺管的三维管线数值模型,用广义α积分对铺设系统进行动力迭代求解,采用Fortran语言编写程序,将静力分析结果与Orcaflex计算结果对比,验证了理论模型的正确性。最后结合算例分析了垂荡和纵荡运动下,张紧器张力变化情况,以及垂荡运动时管线的有效张力、弯矩、速度和加速度的变化情况。
集中质量法;S型铺管;广义α积分;离散型托管架
0 引言
深水S型管线铺设时,由于管线受到巨大的环境载荷,因此安全问题备受人们的关注[1、2]。近年来,人们对管线铺设分析做了很多研究,由于管线受到的载荷非线性、边界条件非线性以及管线本身材料的非线性等因素,所以难以求得解析解[3、4],因此许多学者提出相应的理论模型和数值方法来解决该问题。
Li Z G[5]和龚顺风[6]基于刚悬链线理论建立管线单元的静态平衡控制方程,推导出从铺管船到海床整个管线形态方程的解。在此基础上对铺管参数敏感性进行分析,包括水深、管径、托管架长度对整个S型铺设系统的影响,同时考虑不同参数对张紧器张力、管线极限铺设水深、管线弯矩和轴力的影响,并提出指导性意见。
Gullik A J[7]采用非线性动力偏微分方程求解从船上到海底段的悬跨段管线安装时,模型使用承受有限拉伸、剪切、扭转以及弯曲的三维梁单元,并考虑铺设过程中的恢复力、水动力的拖曳力和海底接触的影响,该模型还可以计算动力定位和低航速铺管船的动力响应。
Pollio A, Langley R L, Low Y M[8]基于集中质量法理论,建立大变形柔性立管的受力模型,模型考虑了立管上由于波浪和水动力载荷引起的外力,立管上端点的位移由铺管船决定,此外还考虑了立管的剪力。在此基础上对比分析了时域和频域下的计算结果,证明了频域计算结果更高效,且与时域计算结果相近。Chai Y T, Varyani K S[9]采用集中质量法理论,建立海底管线受力模型,用于分析不规则海底的影响。将海底看成带阻尼的弹簧模型,用有限差分法离散方程并求解,该方法还可以很好的用于分析系泊缆、刚性和柔性立管。
集中质量法由于其数学模型简单、易收敛,一经提出就收到广泛的关注,但是学者多将该理论用于计算悬垂段管线,少有将该理论用于计算包括托管架在内的整个S型管线铺设的分析计算。该文采用集中质量法原理,忽略阻尼、摩擦和扭转,推导S型铺设时管线的受力平衡方程,考虑了海床、托管架和海流对管线的影响,建立离散型托管架的三维管线有限元模型,用Fortran语言编写计算程序对管线进行动力分析。
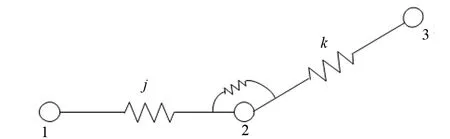
图1 集中质量法单元简化示意图
1 集中质量法模型

1.1 轴向拉力和弯曲剪力
根据集中质量法原理,分别用一个拉伸弹簧和弯曲弹簧来模拟管线受到的轴向拉力和弯曲剪力,则拉伸的应变能和弯矩弹簧的势能可写成[10]:

式中:lj为单元j原长;E为杨氏模量;A为管道横截面积;θ为单元j和k的夹角;I为惯性矩。
将能量对位移求导就能得到轴向拉力和弯曲剪力的计算式:


1.2 海床接触力
为了模拟管线与海床接触时的作用力,该文将海床接触力用一组无质量的弹簧代替(如图2所示)。
假设海底刚度ksb是线性的,管道直径为D,那么单元j中,对于节点i(i=1,2),海床接触力可写成:
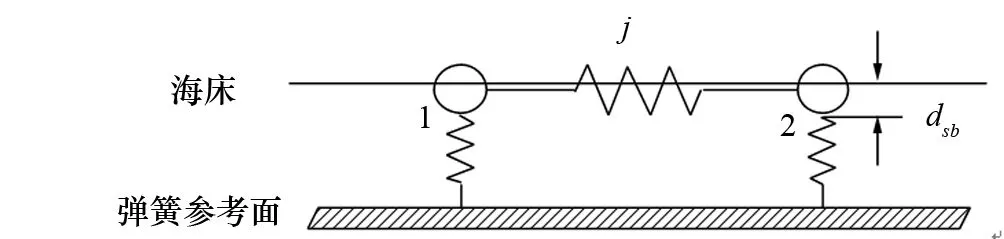
图2 海床模型示意图
式中:Asb为与海床接触面积,近似的可以用公式Asb=D·lj来计算;dsb为渗入海床深度,dsb=0.5D-yi3。
1.3 托管架接触力
管线和托管架的滚轴接触示意图如图3所示:

图3 管线和托管架的滚轴接触示意图




假设管线和滚轴间的接触刚度记为ks,则接触力Fs为:
ν)·
式中:Rr为滚轴的半径。
2 动力分析
在动态的时域分析时必须先进行静态的分析,由于是非线性、大位移问题,所以必须进行迭代求解。用自然悬链线理论计算出一个初始形态,并在此基础上进行求解,具体的计算过程与动态迭代计算相似,但是忽略了惯性力和附加质量,并且不考略管线自身的速度与加速度。

Δ
不考虑阻尼项,则动态迭代平衡方程可写为:
式中:M=Ms+Ma,Ms为管线自身的质量矩阵,Ma为附加质量矩阵。
为了计算出Δy,用Newton-Raphson法对f进行泰勒展开并保留一阶项,这样就有:
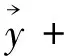
式中:ε为迭代过程中对Δy的修正值;J为雅克比矩阵,其值为:
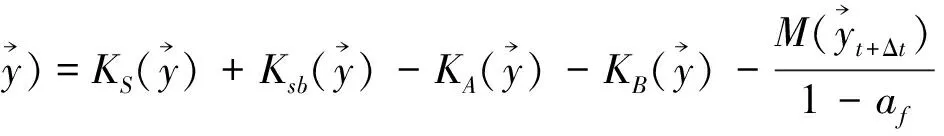
Ks(y),Ksb(y),KA(y),KB(y)分别为托管架总刚度矩阵、海底总刚度矩阵、拉伸和旋转的总刚度矩阵,求解方程(14)就能解决该问题。
3 算例
以某深水S型铺管船为例,管线外径D=0.609 6m,干重We=436.94kg/m,弯曲刚度EI=4.959×108N·m2,轴向EA=1.18×1010N·m2,海床刚度ksb=105N/(m·m2),海流阻力系数CD=1.2,管线总长L=2 390m,管线两端水平距离Ht=1 800m,海水深度hw=1 175m,滚轴与管线的接触刚度ks=1.5×104KN/m,流剖面如图4所示。规定海底的向坐标值为0,数值向上为正,管线与海底接触一端端点向坐标值为0,建立笛卡尔坐标系,那么滚轴位置如图5所示。

图4 流剖面 图5 托管架滚轴位置图
图6~图9为静力计算结果,管线的形态、弯矩和张力与软件计算结果都吻合的非常好,这说明了该文数值模型建立的正确性。

图6 静力计算管线形态 图7 静力计算管线弯矩

图8 静力计算托管架段管线弯矩 图9 静力计算管线有效张力
动力分析过程中,假设张紧器与托管架运动情况相同,没有相对运动。由于波浪对管线的作用力很小,只是集中在海平面附近,随着海水深度增加,波浪对管线的作用力迅速减小为0,而在海平面附近,由于有托管架的存在,波浪力引起的管线变形基本被托管架的支反力抵消,所以波浪力对管线的作用力很小,而且由其引起的管线变形几乎可以忽略[12],所以该文不考虑波浪对管线的直接作用。为了研究铺管船垂荡和纵荡运动对管线和张紧器的影响,假设垂荡和纵荡运动周期都为4π,振幅为1m。取稳定段90s的运动情况如图10所示。
图11为张紧器张力变化的时历曲线,可见当垂荡和纵荡为简谐运动时,张紧器的张力变化也近似是简谐的,运动周期与托管架运动周期相同,相位角相差π,而且垂荡运动时,张紧器的张力变化更剧烈,算例中变化幅度是纵荡运动的2.4倍,这表明张紧器张力对于垂荡运动更敏感。

图10 托管架运动时历曲线 图11 张紧器张力变化时历曲线
图12、图13为垂荡运动弯矩、轴向张力的包络线。对整个管线来说,轴向张力变化比较均匀,除了触底段与离开托管架段管线弯矩变化剧烈外,其它位置弯矩几乎不变,而且垂荡运动的变化幅度更大。离开托管架段管线弯矩变化大于其它地方,容易发生破坏,需要格外注意。

图12 垂荡运动有效张力包络线 图13 垂荡运动弯矩包络线
图14、图15是垂荡运动管线的速度变化包络线。从图中可以看出,加速度的最值包络线变化趋势与速度基本一致,海底段管线由于海底的约束作用,速度变化较小,在触地点处,管线的速度呈现出较大的波动性,速度的最大值达到了0.93m/s,之后速度最大值慢慢减小,在托管架段由于滚轴的约束,管线速度变化的最值基本等于托管架运动的速度最值,即最小值为0,最大值为0.5m/s。加速度与速度类似,海底段管线加速度变化较小,触地点变化最大,最大值为0.64m/s,托管架段管线加速度最小值为0,最大值为0.25m/s。

图14 垂荡运动速度变化包络线 图15 垂荡运动速度变化包络线
在研究不同运动周期对张紧器受力影响时,运动依然是简谐的,运动幅值为1m,运动的圆频率分别取0.5rad/s、0.562 5rad/s,0.62 5rad/s,0.678 5rad/s,0.75rad/s、0.812 5rad/s,仍取稳定段90s的运动作为研究对象,图16为张紧器张力的最大值和最小值随圆频率变化的曲线。当铺管船运动的圆频率越来越大时,张紧器张力的最大值越来越大,张力最小值越来越小,呈线性变化趋势。铺管船垂荡运动幅值变化对张紧器张力的影响如图17所示,运动的圆频率取0.5rad/s,运动幅值分别取0.5m、0.75m、1m、1.25m、1.5m,
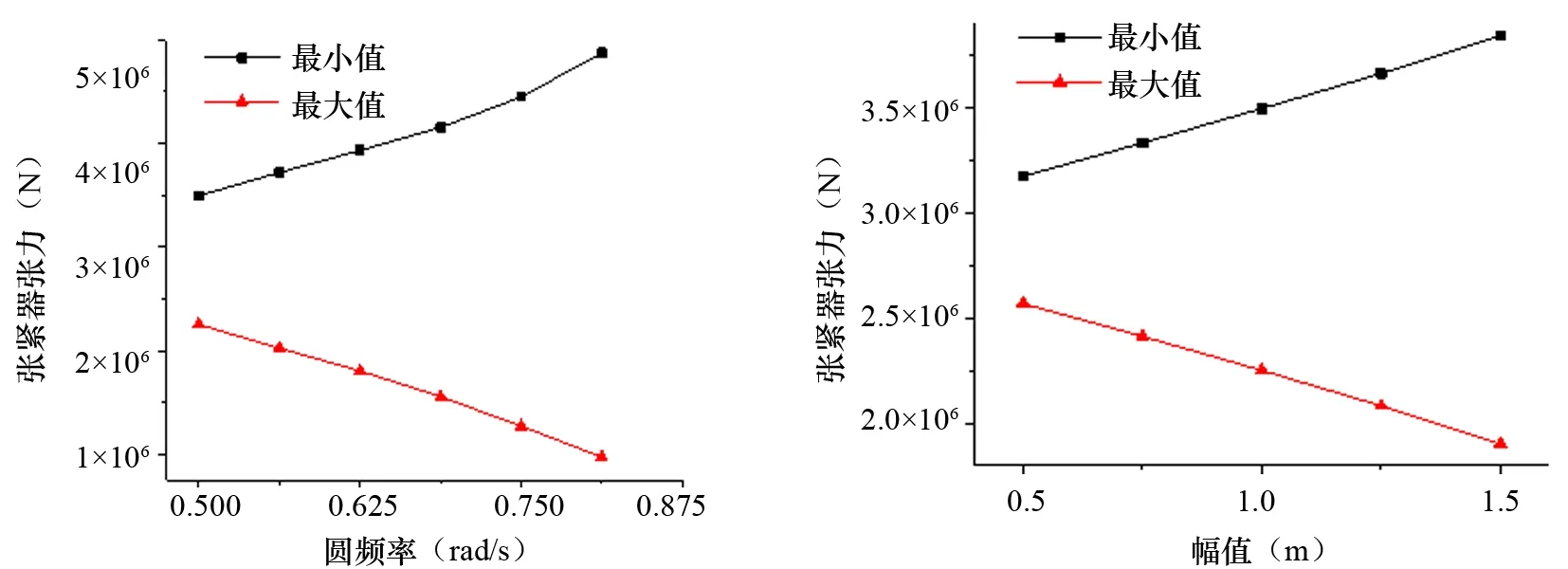
图16 张紧器张力随圆频率变化曲线图 图17 张紧器张力随运动幅值变化曲线
与圆频率变化规律类似,当垂荡的幅值不断增大时,张紧器张力最大值越来越大,而张力最小值则越来越小,变化趋势为线性的。所以实际铺管过程中,需要减小铺管船垂荡的运动周期和运动幅度,这就对动力定位系统提出了较高的要求,同时这也是铺管作业需要在海况良好的条件下进行的原因之一。
4 结论
该文基于集中质量法,推导深水S型铺管的管线受力计算公式,建立三维数值模型,并用广义α积分求解方程,将静力计算结果与商业软件结果对比,两者十分吻合,这说明了程序的正确性。最后结合算例进行动力响应研究,得出结论如下:
(1) 托管架作垂荡和纵荡简谐运动时,张紧器的张力变化也近似为周期相同、相位相差的简谐变化。和纵荡运动相比,垂荡运动对张紧器张力的影响更大。垂荡运动时,整个管线张力变化幅度与张紧器张力变化相同,除了触底段和与离开托管架段管线弯矩变化较大外,其它位置弯矩几乎不变。
(2) 垂荡运动时,悬垂段管线的速度和加速度波动性较大,运动剧烈,其中触地点附近管线运动速度和加速度变化最大。
(3) 张紧器张力对运动的圆频率和运动幅值较为敏感,圆频率越大,周期越小,张紧器需要提供张力的最大值就越大,且张力变化幅度越大;运动幅值越大,张紧器的张力值就越大,张力变化幅度也越大。
(4) 在铺管船发生垂荡运动时,张紧器张力和弯矩变化较纵荡运动大,因此要尽量避免铺管作业时船舶发生垂荡运动,并且离开托管架段的管线弯矩变化较大,更易发生破坏。
[ 1 ] Sun Li-ping,Wang De-jun, Ai Shang-mao.The Simulation and Sensitivity Analysis of S-Lay Installation in Deep Water[J], Applied Mechanics and Materials, 2012,(12):59-64.
[ 2 ] Stelios K, Edmundo C. Mechanics of Offshore Pipelines[M].Elsevier Science Ltd,2007.
[ 3 ] 党学博.海底管道铺设技术研究进展[J]. 中国海洋平台, 2010,25(05):5-10.
[ 4 ] Bai Yong,Bai Qiang . Subsea Pipelines and Risers[M]. Elsevier Science Ltd, 2005.
[ 5 ] Li Z G.Configuration of Submarine Pipeline for Deepwater S-lay Technique[C]. in International Offshore and Polar Engineering Conference.Beijing China,2010.
[ 6 ] 龚顺风,何勇. 深水海底管道S型铺设参数敏感性分析[J].海洋工程,2009,27(4):87-95.
[ 7 ] Gullik A J. A Nonlinear PDE Formulation for Offshore Vessel Pipeline Installation[J]. Ocean Engineering, 2010,37:365-377.
[ 8 ] Pollio A,Langley R L,Low Y M. A Comparison of Time Domain and Frequency Domain Analysis of a Flexible Marine Riser undergoing Large Deformation by Using a lumped mass approach[C]. International Offshore and Polar Engineering Conference,2006.
[ 9 ] Chai Y T, Varyani K S, Barltrop N D P. Three-dimensional Lump-Mass formulation of a catenary riser with bending, torsion and irregular seabed interaction effect[J]. Ocean Engineering,2002,29:1503-1525.
[10] Low Y M, Robin S L. Dynamic Analysis of a Flexible Hanging Riser in the Time and Frequency Domain[C].In: Proceedings of the 25th International Conference on Offshore Mechanics and Arctic Engineering. Hamburg, Germany: ASME,2006.
[11] Chung L, Hulbert G M. A Time Integration Algorithm for Structural Dynamics with Improved Numerical Dissipation: The Generalized-α Method[J].Journal of Applied Mechanics, 1993,(6):371-375.
[12] 党学博. 深水海底管道S型铺设设计理论与计算分析方法研究[D].浙江:浙江大学.2010.
[13] 聂武,孙丽萍. 船舶计算结构力学[M]. 哈尔滨:哈尔滨工程大学出版社,2003.
Dynamic Response of S-lay Method for Deepwater Pipeline Based on Lumped Mass Method
SUN Li-ping1, SONG Huan-feng2, AI Shang-mao1
(1. Harbin Engineering University, Harbin 150001, China; 2. China Ship Scientific Research Center, Shanghai 200011, China)
When pipelaying by S-lay method in the deepwater, pipeline suffers from a huge environmental load. It’s necessary to simulate the pipeline’s force to guarantee the safety of the pipeline. Pipeline equilibrium equation is derived based on the lumped mass method. Considering the seabed,stinger and current, a three-dimension force model for S-lay method in the deepwater is built. Generalized-α is used to solve the dynamic analysis with a discrete stinger, using Fortran program. Comparison of the static results with Orcaflex’s results shows that the correctness of the theoretical model. The change of tensioner force is calculated in heave and surge, and the range of pipeline’s effective force , bending moment velocity and acceleration is calculated in heave.
lumped mass method; S-lay method; generalized-α; discrete stinger
2014-03-29
3000米水深大型起重铺管船自主研发项目(COOEC),深海工程科学与技术创新引智基地计划基金(B070019)。
孙丽萍(1962-),女,教授。
1001-4500(2015)02-0070-07
P75
A

