我国极端降水阈值确定方法的对比研究*
迟潇潇,尹占娥,王 轩,孙钰科
(上海师范大学 旅游学院 地理系, 上海 200234)
我国极端降水阈值确定方法的对比研究*
迟潇潇,尹占娥,王 轩,孙钰科
(上海师范大学 旅游学院 地理系, 上海 200234)
在全球变暖趋势下,极端降水频发,引起了国内外学者的广泛关注,而极端降水阈值的确定是研究极端降水事件的起点。基于中国499个气象站点1960-2009年的逐日降水数据,采用DFA法、百分位法和Pearson-III概率分析法,对中国各站点及区域的极端降水阈值进行对比分析。结果表明:DFA法确定的极端降水阈值远大于百分位法确定的极端降水阈值,约为Pearson-III两年一遇情景下的极端降水;中国极端降水阈值从东南沿海向西北内陆递减,其中四川盆地边缘地区、长江中下游流域地区和华南地区南部极端降水阈值最大;南方地区、北方地区、青藏地区和西北地区的建议极端降水阈值分别为80 mm、50 mm、25 mm和20~25 mm。
极端降水;阈值;DFA;中国
20世纪末期以来,全球气候变化显著,因极端降水引发的洪水、泥石流等自然灾害频发,对社会稳定、经济发展和人民生活产生了严重影响[1-2]。根据国际政府间气候变化组织(IPCC)第五次评估报告显示,由于全球变暖和大气水汽增加,极端降水的频次和强度均有所增加,并有持续增加的趋势,降水将更趋于集中[3]。近年来很多国家遭受了暴雨袭击,并由此引发了一系列灾难性的后果。由于人口密度大,排水设施不健全,土地利用不完善等原因,极端降水对发展中国家的影响更为显著[4]。例如,2012年北京暴雨,造成79人死亡,直接经济损失116.4亿元;2013年台风“菲特”引发强降雨,导致浙江435.1万人受灾,经济损失47.37亿。确定极端降水阈值是研究极端降水的起点。确定极端降水阈值的方法有很多,最常见的是固定阈值法、参数法和非参数法。固定阈值较适用于气候变化较小的范围,不适用于跨度广泛的研究区域[5]。我国一般采用中国气象局确定的国家标准定义不同等级的降水。目前国际上在气候极值变化研究中最常见的是采用某个百分位值作为极端降水阈值,超过这个阈值的降水称为极端降水,常用的百分位有第90、95和第99个百分位[6]。在水文领域最常用的是概率分析法,如Pearson-III概率分析法。该方法具有广泛的概括和模拟能力,在气象上常用来拟合最大日降水量等级分布,推求最大日降水量的重现期[7-9]。
气候系统的变化具有自记忆特征,因而在表征气象要素的时间序列中蕴含着长程相关性,即系统的演化具有持续性[10]。由于极端气候事件是系统演化的极端状态或是系统受到外界扰动的异常状态,偏离系统自身演化的范畴,去趋势波动分析(Detrend Fluctuation Analysis, DFA)得到的DFA指数可以衡量系统在某一时间尺度内演化的长程相关,理论来说系统整体的长程相关性不受极端气候事件的影响或影响很小[11]。近年来,DFA法被成功地用于研究气候和极端事件的长程相关性[12-14]。
因此,本文基于中国1960-2009年499个气象站点的逐日降水数据,采用DFA法、百分位法和Pearson-III概率分析法确定各站点的极端降水阈值,通过分析它们的空间分布规律,以期为中国各站点及区域提供一个更加准确可靠的极端降水阈值标准。
1 数据来源与研究方法
1.1 数据来源及预处理
本文研究数据是由“中国气象科学数据共享服务网”提供的756个站点1960年1月至2009年12月的逐日降水数据(http://cdc.cma.gov.cn),考虑到时间序列的连续性,剔除数据缺失及数据不连续的站点,最终选取499个站点日降水量数据用于数据分析(图1)。
应用Matlab软件对499个站点的数据做了如下处理:筛选降水量不等于零的数据,按DFA法、百分位法计算极端降水事件阈值,挑选出每年最大日降水量,用Pearson-III概率分析法确定不同重现期下的极端降水阈值,计算年均降水量。将处理后的站点数据导入ArcGIS10.1中,并与中国政区图(1:25 000 000)进行叠加,用Kriging插值得到DFA阈值、百分位阈值、Pearson-III不同重现期下阈值、年均降水量的空间分布,将空间分布图与中国立体DEM图进行叠加。根据中国自然地理区划,将研究区域划分为四个地区——西北地区、青藏地区、北方地区和南方地区(图1)。

图1 中国四大自然地理区划及气象站点分布图
1.2 研究方法
1.2.1 DFA法
去趋势波动分析法是Peng等一些生物学家在探测DNA内部分子链的相关可能性程度时提出的[15],并广泛应用于生物、物理、气候等多个领域。它是基于随机过程理论和混沌动力学的一种分析方法,计算基本步骤如下所示。
第一步 建立一个时间序列xk(k=1,…,N),得到一个新序列:

(1)
式中:
第二步 将新序列y(i)划分为长度为s的不重叠等长度子区间,长度为N的序列共被分为Ns=int(N/s) 个字区间。因序列长度N不一定被子区间长度s整除,为保证原序列信息不丢失,可以从序列末端开始反向前再划分一次,这样可得到共2Ns个子区间。
第三步 对每个子区间v(v=1,2,…,2Ns) 的数据进行多项式回归拟合,得到局部趋势函数yv(i)。yv(i)可以是一阶、二阶或更高阶的多项式,分别记为DFA1,DFA2等。消除各子区间内趋势,计算其方差均值:
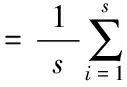
(2)
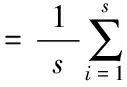
(i=Ns+1,Ns+2,…,2Ns)。
(3)
第四步 确定全序列的q阶波动函数:
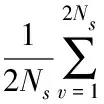
(4)
式中:q可以取为任何非零实数。q=0时,式(4)变为:

(5)
第五步 通过分析双对数坐标图Fq(s)∝shq的关系,可以确定波动函数的标度指数hq,即存在幂律关系:
Fq(s)∝shq。
(6)
研究表明标度指数hq和系统的长程相关性相关。当0.5 1.2.2 百分位法 本文采用国际学术界较为通用,且在国内研究中常用的百分位法来定义极端降水阈值,当某站某日的日降水量超过该阈值时就认为该站该日出现了极端降水[17]。常用的百分位有第90、95和99个百分位。其具体做法是把1961-2009年逐年的日降水量按升序排序,将第90、95或99个百分位值的50年平均值定义为极端降水事件的阈值。 1.2.3Pearson-III型概率计算 极端事件可以根据重现期来描述[18]。频率分析被广泛地用来计算极端降水事件的重现期,本文采用的是频率计算法中在美国和中国最常用的Pearson-III型概率计算方法。考虑到DFA法和百分位法确定阈值最可能的重现期,本文选取了计算结果中重现期为1年和2年情景下的极端降水事件阈值进行对比分析。 2.1 极端降水阈值对比 通过对比中国降水强度等级划分标准(表1)与百分位法、Pearson-III概率分析法和DFA法确定的部分省会城市的极端降水阈值(表2)可知,第90个百分位(90th)与第95个百分位(95th)确定的极端降水阈值较为接近,均小于50mm,大都介于国家标准的中雨至大雨强度。第99个百分位(99th)确定的阈值远大于90th与95th百分位法所确定的,大部分站点大于50mm,为国家标准的暴雨强度。Pearson-III概率分析法确定的阈值远大于90th、95th百分位法所确定的阈值,且10年重现期下的极端降水阈值几乎为99th百分位法所确定阈值的两倍,这种差异主要是由于统计方法的不同所引起的。DFA法确定的阈值跨度范围大,从大雨到大暴雨均有出现,且大于百分位法所确定的阈值,与两年一遇极端降水阈值大小相近。 表1 降水强度等级划分标准(内陆部分) 表2 百分位法、概率分析法、DFA法确定的极端降水阈值 mm 2.2 极端降水阈值空间分布对比 极端降水与年降水量之间存在较好的相关性,本文选用DFA阈值、99th百分位法阈值、Pearson-III两年一遇情景下极端降水阈值和年均降水量的空间分布来探索中国极端降水的空间变化规律(图2)。我国的年降水量自东南沿海向西北内陆递减,DFA法、百分位法和Pearson-III概率分析法确定的极端降水阈值的空间分布规律与我国年降水量的空间分布规律总体一致。 在同一区域内,DFA法确定的极端降水阈值大于99th百分位法确定的,大部分地区的差值在25mm左右,东南地区尤为明显,这主要是由于我国东南地区距离海洋较近,长期受到来自海洋的季风(西南季风和东南季风)影响。DFA法确定阈值的大值区域主要位于华南南部,长江中下游流域以及四川盆地,均大于100mm;在西部阈值较小的地区大值主要出现在天山山脉乌鲁木齐以及北塔山地区,大于25mm(图2a)。百分位法确定的阈值在海南省、广西南部和广东南部的极小部分区域大于100mm,在西部地区未出现阈值较大的区域(图2b)。在四川盆地边缘地区,DFA法确定的阈值与99th百分位法确定的阈值差值大于50mm。这主要是由于四川盆地位于长江上游,特殊的地形和地理位置使该地区长期受对流天气以及水文系统的长程相关性影响,边缘地区多高山,所受影响更大。可见DFA法与百分位法所确定阈值的差异,主要是由于DFA法考虑了气候系统的长程相关性。 (a) DFA法阈值 (b) 99th百分位法阈值 (c) Pearson-III阈值(重现期2年) (d) 年降水量 DFA法确定极端降水阈值的空间分布与Pearson-III重现期为两年情景下的极端降水阈值空间分布极为吻合(图2c),与年降水量的空间分布较为吻合(图2d)。因此用DFA法来定义中国的极端降水阈值更具合理性。 2.2 四大自然区划建议阈值 确定一个站点或区域的极端降水阈值不仅要考虑日降水量,还需要考虑地形、排水能力等影响因素。为了提出合理的中国极端降水阈值标准,我们将研究区按照自然地理区划划分为四个区域——西北地区、青藏地区、北方地区和南方地区。南方地区阈值为41~225mm(表3),大部分地区介于75~100mm之间,虽然南方地区地形较低,但整体排水能力较强,所以80mm可为南方地区的极端降水阈值。青藏地区阈值为13~37mm(表3),青藏地区地势较高、排水能力一般,25mm可为青藏地区的极端降水阈值。西北地区大都为高原地区,排水能力较弱,且日极端降水量较小,大部分区域小于25mm,因此20~25mm可为西北地区的极端降水阈值。北方地区阈值为32~132mm跨度较大,且地形变化多样,使该地区的阈值较难确定,由于50mm左右区域面积较大,所以50mm可为北方地区的极端降水阈值。 表3 DFA法确定的四个地区的极端降水阈值 mm 本文以中国为研究区域,采用DFA法、百分位法、Pearson-III概率分析法确定极端降水阈值,结合年降水量的分布规律,通过对比分析,认为用DFA法确定中国的极端降水阈值更具合理性,可以在全国尺度上更好地理解极端降水。DFA法确定的极端降水阈值远大于百分位法确定的阈值,约是重现期两年一遇情景下的极端降水。与许多学者在区域尺度上研究极端降水结论一致[14]。极端降水的空间分布与年降水量的空间分布规律一致,表现出从东南沿海向西北内陆递减的规律,其中四川盆地边缘地区、华南地区和长江中下游流域极端降水阈值最大。根据各区降水、地形和排水能力,我们给出中国四大区划的建议阈值为:南方地区80mm、北方地区50mm、青藏地区25mm、西北地区15~25mm。四大区划极端降水阈值的建议,可以为各地区强降水预警提供参考。 尽管应用DFA法已得到各站点的日极端降水阈值,但仍然存在一些问题。有时DFA法的收敛值很难确定,这可能会导致个别站点阈值的不确定性,后期可将DFA法与替代数据法相结合[19],更加准确地确定收敛点,进而定义更加精确的极端降水阈值。并且该方法需要在不同区域进行验证。为了更好地探索中国极端降水的变化规律,今后可根据已确定的阈值着重研究极端降水在中国的时空变化趋势。 [1]ChangnonSA,PielkeJrRA,ChangnonD,etal.Humanfactorsexplaintheincreasedlossesfromweatherandclimateextremes[J].BulletinoftheAmericanMeteorologicalSociety, 2000, 81(3): 437-442. [2] 尹占娥, 许世远. 城市自然灾害风险评估研究[M]. 北京: 科学出版社, 2012. [3]IPCC2013.Climatechange2013:Thephysicalsciencebasis.contributionofworkinggroupItothefifthassessmentreportoftheintergovernmentalpanelonclimatechange[M].CambridgeUniversityPress, 2013. [4]MirzaMMQ.Climatechangeandextremeweatherevents:candevelopingcountriesadapt? [J]Climatepolicy, 2003, 3(3): 233-248. [5] 杜海波, 吴正方, 张娜, 等. 近60a丹东极端温度和降水事件变化特征[J]. 地理科学, 2013(4): 473-480. [6] 翟盘茂, 潘晓华. 中国北方近50年温度和降水极端事件变化[J]. 地理学报, 2003, 58(Supp.1): 1-10. [7] 高绍凤, 陈万隆, 朱超群, 等. 应用气候学[M]. 北京: 气象出版社, 2001. [8] 林两位, 王莉萍. 用Pearson-III概率分布推算重现期年最大日降雨量[J]. 气象科技, 2005, 33(4): 314-317. [9] 陈海泉, 罗碧瑜, 李凌志, 等. 用Pearson-III分布推算梅州最大一日降水量的重现期[J]. 中国防汛抗旱, 2008(4): 24-26. [10]王启光, 张增平. 近似熵检测气候突变的研究[J]. 物理学报, 2008(3): 1976-1983. [11]封国林, 侯威, 杨萍. 极端气候事件的检测、诊断与可预测性研究[M]. 北京: 科学出版社, 2012. [12]KurnazML.Applicationofdetrendedfluctuationanalysistomonthlyaverageofthemaximumdailytemperaturestoresolvedifferentclimates[J].Fractals, 2004, 12(4): 365-373. [13]ChenX,LinG,FuZ.Long-rangecorrelationsindailyrelativehumidityfluctuations:AnewindextocharacterizetheclimateregionsoverChina[J].Geophysicalresearchletters, 2007, 34(7): 1-4. [14]ZhangQ,ZhangJ,YanD,etal.Extremeprecipitationeventsidentifiedusingdetrendedfluctuationanalysis(DFA)inAnhui,China[J].TheoreticalandAppliedClimatology, 2014, 117(1/2): 169-174. [15]PengCK,BuldyrevSV,GoudbergerAL,etal.FinitesizeeffectsonlongrangecorrelationimplicationsforanalyzingDNAsequences[J].Nature, 1999, 397(11): 498-500. [16]杨萍, 侯威, 封国林. 基于去趋势波动分析方法确定极端事件阈值[J]. 物理学报, 2008(8): 5333-5342. [17]BonsalBR,ZhangX,VincentLA,etal.CharacteristicsofdailyandextremetemperaturesoverCanada[J].JournalofClimate, 2001, 14(9): 1959-1976. [18]Goubanova,K.,Li,L.ExtremesintemperatureandprecipitationaroundtheMediterraneanbasininanensembleoffutureclimatescenariosimulations[J].GlobalandPlanetaryChange, 2007, 57(1), 27-42. [19]侯威, 章大全, 周云, 等. 一种确定极端事件阈值的新方法: 随机重排去趋势波动分析方法[J]. 物理学报, 2011(10): 790-804. AComparisonofMethodsforBenchmarkingtheThresholdofDailyPrecipitationExtremesinChina Chi Xiaoxiao, Yin Zhan’e, Wang Xuan and Sun Yuke (CollegeofTourism,ShanghaiNormalUniversity,Shanghai200234,China) Precipitationextremeshavebecomemorefrequentunderglobalwarming,whichattractwidelyattentionofscholarsathomeandabroad,andtheappropriatethresholdisthefirststepofstudyingprecipitationextremes.Inthispaper,weusedatasetsofdailyprecipitationrecordedin499meteorologicalstations,throughthecomparisonofDFAmethod,percentilemethodandPearson-IIIdistributiontodefinetheproperthresholdforeachstationandeachregion.Resultsshowthat:ThresholdscalculatedbyDFAaremuchhigherthanthepercentilemethodandthevaluesarearoundthereturnperiodoftwoyears.ThresholdsdecreasingfromsoutheasterncoastalareastonorthwesterninlandsandthresholdsarethehighestinSichuanBasin,middleandlowerYangtzeRiverandsouthernpartofSouthChina.Oursuggestthresholdsinfourmajorregions-SouthChina,NorthChina,Qinghai-TibetRegionandNorthwestChinaare80mm, 50mm, 25mmand15~25mm. precipitationextremes;thresholds;DFA;China 2015-01-29 2015-03-11 国家自然科学基金(41371493, 41201550, 41071324);上海市教委科研创新项目(13YZ061);上海师范大学研究生优秀成果(学位论文)培育项目(A-6001-14-001210) 迟潇潇(1990-),女,山东青岛人,硕士研究生,主要从事极端天气及风险研究. E-mail:myxiaoxiaoer@163.com 尹占娥(1963-),女,山西兴县人,博士,教授,主要从事城市地理与公共安全研究. E-mail:zhaneyin@126.com P468;X43 A 1000-811X(2015)03-0186-05 10.3969/j.issn.1000-811X.2015.03.034 迟潇潇,尹占娥,王 轩,等. 我国极端降水阈值确定方法的对比研究[J].灾害学, 2015,30(3):186-190. [Chi Xiaoxiao, Yin Zhan’e, Wang Xuan,et al. A comparison of methods for benchmarking the threshold of daily precipitation extremes in China[J].Journal of Catastrophology, 2015,30(3):186-190.]2 结果分析





3 结论与讨论

