灌区计量弧形闸门参数化有限元分析及结构改进

尚恒建， 徐宏海

（北方工业大学 机电工程学院，北京 100144）

0 引言

我国是水资源严重紧缺国家，农业用水特别是渠灌区水资源利用率低，浪费严重，其主要原因是没有具有计量功能的闸门。为此，我国山西运城等地区在水利部“948”计划资助下，从澳大利亚引进了FlumeGate等产品，但价格昂贵、安装条件苛刻，而且从其运行状况来看，存在以下问题：一是不能实现闸门的远程控制；二是分水信息数据通过局域无线网进行传输，灌区范围小于方圆10km；三是无手动功能。目前，国内尚无此类定型产品。为此，采用APDL对弧形闸门门板进行参数化建模并进行有限元分析，找出加强筋间距、板厚等关键结构参数对闸门变形的影响规律，对于弧形闸门的国产化设计具有较大的参考价值。

1 弧形闸门的结构分析及参数化建模

1.1 结构及分析

闸门体是由3块铝合金复合板组成。门板的重量对启闭传动系统的输出力矩有重要影响，为减轻门板的重量，同时满足门板在水压作用下的强度和刚度要求，设计了一种基于蜂窝技术的轻型高强铝合金复合门板，门板主体框架和加强筋（截面如图1所示，图中H为加强筋间距，B为框架宽度，R为弧形板半径，S为闸门跨度）由高强铝合金制作，型腔内填充铝蜂窝,然后压粘铝合金面板，具有重量轻、刚度好、不生锈等优点。两侧的扇形铝合金板依靠驱动装置对钢丝绳的传动力来改变闸门开度的大小，从而将闸门开启或者关闭。弧形板与挡水板由螺栓连接，门板内侧用螺栓固定支架，从而保证挡水板和弧形板的可靠连接。闸门外框架固定在预制闸室内，内框架和闸门的其他组成部分作为一个整体嵌入外框架［1］。

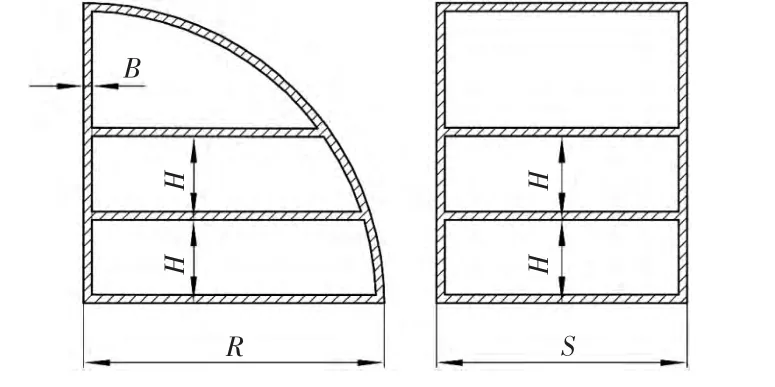
图1 弧形板、挡水板的门框截面图

1.2 参数化建模

1.2.1 ANSYS建立简化有限元模型

ANSYS有限元模型的建立主要有3种方法：一是在ANSYS中直接构建实体模型；二是导入由其他平台建立的CAD模型；三是直接生成节点和单元［2］。本例中，由于模型比较复杂，而且需要进行多次有限元分析，故选择第一种方法，采用APDL进行弧形闸门的参数化建模，只需要修改相应的参数即可完成整个分析过程。闸门三维参数化建模时，所做的简化如下：由于在实际应用中，两侧的弧形板和挡水板之间并无脱离现象，并且着重分析门板的变形，所以门板之间的螺栓连接均做固结处理，从而简化了计算，避免了复杂的接触分析以及可能由此出现的结果不收敛。另外，去掉对我们的分析不重要的圆角、支架，降低了参数化建模的难度。总之，建模一定要综合考虑前后处理参数化的可行性和方便性。

1.2.2 蜂窝板的建模

弧形闸门门体可以看作是经加强筋加固的铝蜂窝板。铝蜂窝板采用高强度铝合金板作为面板与底板，涂覆以耐腐蚀环保黏合剂，中间用铝蜂窝芯复合制造而成（这里采用正六边形蜂窝夹芯，用料省、制造简单、结构效率高），具有重量轻、刚性好、强度高、寿命长、不易变形、综合功能突出、加工适应性好等优点。此外由于不采用大面积铆接，可以减少应力集中，从而使疲劳强度有较大的提高。由于在ANSYS中没有蜂窝结构的单元库，因此需要对铝蜂窝复合板结构进行等效处理。目前，对正六边形蜂窝板的等效方法主要有3种：三明治夹芯理论、蜂窝板理论和等效板理论［3-6］。其中，等效板理论是指将整个蜂窝夹层板结构等效成等刚度的各向同性的简单板，然后根据刚度相等推导出等效板的弹性模量和厚度。按照等效板理论得到适合实际工程应用的等效弹性模量的工程计算公式为

考虑本例的实际情况，采用等效板理论进行分析。这样，在分析铝蜂窝夹层板的各种问题时，只需分析对应的等效板，因此很大程度上简化了分析，便于各种工程计算，有较高的应用价值。所设置的弧形闸门的初始尺寸为：闸门跨度S=1.5 m；弧形板半径R=1.8 m；加强筋间距H=65 mm；弧形板总厚度T1=75 mm；挡水板总厚度T2=50 mm；铝蒙皮厚度hf=2 mm正六边形蜂窝芯尺寸t×l=0.075 mm×6 mm，其中t为铝箔的厚度，l为正六边形的边长，高度hc=71 mm；材料的弹性模量Ef=70 GPa。代入公式中计算，得到弧形板和挡水板的等效弹性模量分别为3.73 GPa、5.6 GPa。

在记事本中直接编写闸门参数化有限元模型以及分析过程的命令流。首先，建立框架和加强筋的几何模型，因为两者是焊接在一起的，所以使用VADD命令使两者成为一体；其次，建立等效蜂窝板填充，生成简化的有限元分析模型，如图2所示。

1.2.3 框架与等效蜂窝板的连接

分别对主体框架、加强筋和等效蜂窝板进行网格划分。由于模型比较复杂，采用了自由网格划分方式，如图3所示。由于框架与等效蜂窝板是不同的材料，网格划分完毕后，需要对框架和等效板进行连接。它们之间的连接可以选择传统的耦合自由度法和MPC法（多点约束算法）。耦合自由度和约束方程法有一定的局限性，其结果可能依赖于接触刚度，而且即使对小变形问题也需要大量迭代才能达到满意的平衡。MPC法的原理是将不连续、自由度不协调的单元网格连接起来，不需要连接边界上的节点完全一一对应。它提供了一个极为有效的接触模拟算法，接触表面的节点自由度将被自动消除，从而提高求解效率［6］。所以，在这里采用MPC方法连接，从而克服了传统方法对大量节点逐一建立约束方程的缺点，省时省力，计算速度快、精度高。另外，划分网格时，应尽量保证接触面和目标面的网格相似，这样，MPC方法才能给出与连续网格相似的结果。至此，ANSYS的前处理过程基本完成。

图2 闸门的有限元简化模型

图3 闸门的有限元网格

2 求解及后处理

前处理过程完毕后，进入求解器。按照弧形闸门的实际工况，对门板施加约束和载荷（水压力梯度载荷）。选择求解类型为静态分析，其余所有的求解选项使用ANSYS的默认设置。在求解完成之后，ANSYS会出现提示“Solution is done！”。然后进入后处理器。后处理的主要功能是要做到“图文并茂”，既能方便地查找计算结果，又能形象生动地显示出分析对象的各种物理量［6］。

3 结果分析

当闸前水位为1.5 m，闸门关闭挡水时，显示门板的总位移云图如图4所示。由图4可知，左右两侧弧形板边缘处最大变形量达到了0.981 mm，出现在弧形板下边缘处，而挡水板的最大变形为0.819 mm，出现在挡水板2根加强筋中间偏下的位置。为了减小弧形板的变形，同时为了避免钢丝绳的拉力引起弧形板发生轴向变形，在弧形板的外缘加上了两根拉杆。这样，在相同的工况条件下，门板总变形云图如图5所示。门板的最大变形量为0.696 mm，出现在挡水板大约中间的位置。而弧形板的最大变形量为0.116 mm。当闸门由关闭挡水状态（开度为6°）逐渐开启时，门板的受力状态逐渐发生变化，当挡水板顶部开始进入水面后，水开始自由流出。由于闸门开启速度很慢，可以认为挡水板始终受到静水压强的作用。此闸门的最大开度为84°，通过改变闸门的开度，查看变形图，将挡水板的最大变形量绘制曲线图如图6所示。可见，闸门开度越大，挡水板的变形量越大，最大变形量变化范围0.65～1.86 mm。因此，在改变其他参数进行分析时，只需分析这种最危险工况（闸门开度为84°）即可。

图4 无拉杆时门板变形图

图5 加上拉杆后门板的变形图

图6 闸门开启角度对门板最大变形量的影响

3.1 加强筋间距对门板变形的影响

通过改变命令流文件中加强筋间距H，可以方便地得到门板各部位的变形及应力状态云图。当H从0.4m～0.75m变化时，挡水板最大变形的位置逐渐从顶部的蜂窝板向中间的蜂窝板移动。绘制门板加强筋间距与挡水板最大变形量之间的关系曲线，如图7所示。从曲线图7可以看出，当2根加强筋间距在580 mm左右时，挡水板的最大变形量达到最小，约为1.85 mm。

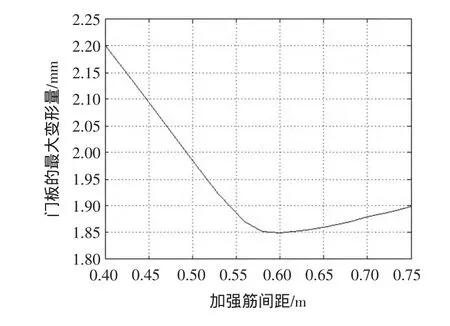
图7 加强筋间距H对门板最大变形量的影响

3.2 板厚对门板变形的影响

取加强筋间距为580 mm，分别改变弧形板和挡水板的厚度，记录每次门板的最大变形量，绘制曲线图，如图8、图9所示。

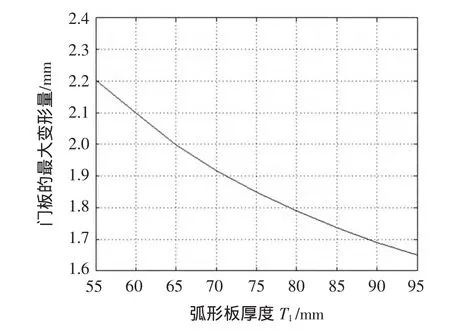
图8 弧形板厚度T1对门板最大变形量的影响

图9 挡水板厚度T2对门板最大变形量的影响

由图8、图9可知，随着弧形板、挡水板厚度的增加，门板的最大变形量逐渐减小，但同时也增加了材料的使用，从而增加了门板的重量。一般取弧形板厚度为75 mm，挡水板厚度为50 mm即可，此时挡水板的最大变形量为1.8 mm左右，弧形板的最大变形量仅为0.3 mm左右，而且保证闸门不至过于笨重。从等效应力云图可知，最大应力为45.7 MPa，出现在闸门的框架上。框架的材料为6063-T5工业铝型材（≥160 MPa），取闸门材料的安全系数为2，则其许用应力为80 MPa，所以满足强度要求。参考《水利水电工程钢闸门设计规范》（DL/T5013-95）规定，闸门的容许挠度值为L/600，则本闸门的容许挠度值为1 500 mm/600=2.5 mm。由图形知弧形板和挡水板的最大形变量分别为0.308 mm和1.849 mm，同样满足刚度要求。为验证上述计算方法的正确性，对此型号的弧形闸门闸前满水位1.5 m情况下门板的变形情况进行实际测试，最大变形在1.8 mm左右，其位置与仿真结果相吻合。实际使用情况表明，1.5 m宽闸门产生2 mm左右挠度并不影响正常使用。

4 结语

采用APDL进行了渠灌区计量弧形闸门的三维有限元整体建模，通过改变参数，得出跨度为1.5 m、弧形板半径为1.8 m的弧形闸门，当2根加强筋间距为580 mm，弧形板和挡水板的厚度分别为75 mm、50 mm时，闸门的最大变形量不足2 mm，同时闸门的用料较少，质量较轻，结构最为合理。

［1］ 杨鲲鹏.测控一体化闸门在汾河灌区的应用［J］.山西水利,2011（9）：40-41.

［2］ 曾攀，雷丽萍，方刚 .基于ANSYS平台有限元分析手册：结构的建模与分析［M］.北京：机械工业出版社，2011.

［3］ 陈昌亚，郑晓亚，姜晋庆.卫星结构优化设计的建模问题［J］.机械科学与技术，2005，24（1）：66-69.

［4］ 赵金森.铝蜂窝夹层板的力学性能等效模型研究［D］.南京：南京航空航天大学，2006.

［5］ 胡玉琴.铝蜂窝夹层板等效模型研究及数值分析［D］.南京：南京航空航天大学，2008.

［6］ 张会杰，祝兵，高飞.Ansys多点约束技术的应用［J］.甘肃科技，2007（2）：169-170.