大型衬套零件加工刀具选择与改制技术

李琦

（渤海船舶职业学院，辽宁葫芦岛125105）

0 引言

不锈钢衬套类零部件是大型柴油机的关键零部件之一，加工存在一定困难，主要在于工件为大型衬套件，且壁厚较薄，具体尺寸为工件直径为φ750mm，长度925mm，壁厚仅25 mm。在加工时一般选用重型卧式车床，易发生加工变形；工件材料一般为1Cr18Ni9Ti，材料韧性较大，易发生粘刀现象，加工材料硬化严重。而且大型车床加工时不易冷却，加工过程中刀具在工件上行走近14 km，在加工后期刀具磨损情况加剧。

为解决此类零件的加工难点，笔者在实践中经过研究发现可以从加工刀具入手加以解决，通过对加工刀具各几何参数进行合理选择与修磨，并采用合理的切削用量，可以获得较好的加工精度及表面粗糙度。

1 刀具几何参数刃磨技术分析

1）主偏角与切削力的关系。对主切削力FZ的影响：当切削面积Ae不变时，主偏角增大，切削厚度增大，而切削宽度减小，切削层形状变为厚而窄，切削力减小。当主偏角增大到60°～75°之后，由于刀尖圆弧半径部份参与切削的比例增大，切削层变薄而宽，主切削力又逐渐增加。对进给抗力和切深抗力的影响，由进给抗力=FMsinKr和切深抗力=FMcosKr（FM在基面中垂直于切削刃的切削分力）两公式可知，进给抗力随主偏角的增大而增大，切深抗力则减小。当Kr=90°时，切深抗力为0。但上两公式是在刃倾角等于零情况下导出的，当不等于零时，即使Kr=90°，切深抗力也不为0，因为刃倾角对进给抗力和切深抗力也有影响。并且在实际切削时，由于具有刀尖圆弧半径和副切削刃参与切削，即使副偏角等于90°时，也存在切深抗力。

2）主偏角、副偏角对刀尖强度和散热的影响。刀尖角加大刀具强度增大，并且散热面积增大，使切削热减小，也减小刀具的耐磨。主偏角增大，刀尖角减小，副偏角加大，刀尖角减小。主偏角减小，刀尖角增大，副偏角减小，刀尖角增大。因此选用60°主偏角和15°副偏角。

3）修光刃与加工表面质量的关系。在精车中修光刃是提高表面粗糙度的首选。但是在车削长孔时修光刃的选择要适中，修光刃过长易引起刀具振动，修光刃小于走刀量又起不到修光作用。在加工此工件时，刀具在工件上行走时间长，选用走刀量过小会使刀具在加工后期产生急剧磨损，选用走刀量大会使表面质量不好，经过计算选用走刀量为0.25 mm，选用修光刃为0.5～0.6 mm。

4）刀具耐磨性与后角及修光刃的关系。后角的存在可以使刀具主后刀面和工件表面的摩擦减小，后角的过分增大会降低刀刃的强度。随着后角的增加，刀具切削刃会锋利，但耐磨性差，后角太小则会与工件产生相互摩擦，产生振动，合理选择后角对此工件加工十分关键。修光刃不光对表面粗糙度有影响，对于刀具耐磨性也有一定的影响。修光刃小，磨损快；修光刃长增加刀具耐磨性，但易引起振动。

5）刀具几何参数与振动的关系。加工中因镗杆刚性差，刀具几何参数选择不合理会产生振动造成工件无法加工。前角增大，切削轻快，不易引起振动。在切削刚性差的工件时采用小的后角和副后角能增加阻尼,防止或减轻振动。主偏角增大，减小切削力，减轻振动。

6）刃倾角和断槽宽度对断屑的影响。刃倾角主要影响刀头的强度和排屑方向，断屑槽的宽窄和方向也决定切屑的排屑方向和断屑问题。因为此工件为不易断屑的不锈钢材料，尤其是精车时，切屑不断绕到车刀上会挤伤工件表面，使表面粗糙度达不到图纸要求，所以经过反复试验用如表1所示精车刀角度。在精车时切削会因重力和刀具挤压变形，在一定长度断屑。

工件毛坯由两半圆型不锈钢板焊接而成，在实际加工中刀杆伸出端近1 m长，故加工刚度较差，在加工中容易产生刀具振动，且很容易损坏刀尖。综合考虑加工过程中各种因素的影响，经过多次试切削，最终通过将YG8螺纹车刀改制成为所需刀具，根据刀具几何参数合理修磨，使加工效率得到提高，工件加工质量达到理想效果。刀具改制的几何参数如表1所示。

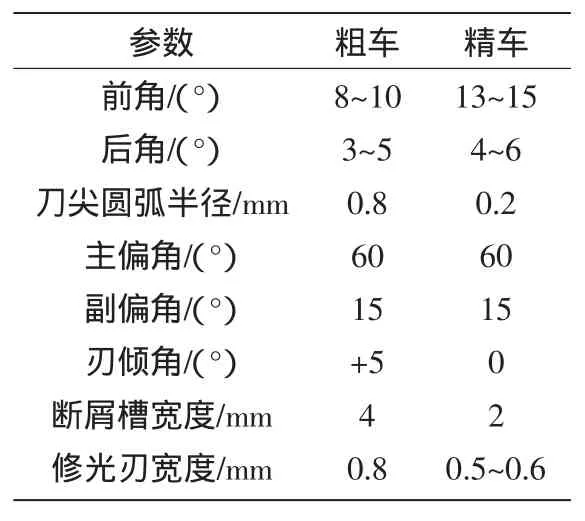
表1 YG8精车刀的几何角度选择

表2 实际加工切削参数

2 切削用量

经过实际加工检验，选择如表2所示的切削参数可以获得较好的加工效果。

3 结论

针对大型衬套类零件的加工难题，通过对YG8螺纹车刀进行改制，采用合理的刀具刃磨技术，修磨出适当的刀具角度，并在实际加工中采用合理的切削参数，可以获得较好的表面质量及加工效果。