金属切削刀具剩余使用寿命的可靠性研究

陈剑， 魏小钧， 张一帆

（中国铁道科学研究院机车车辆研究所，北京100081）

0 引言

金属切削过程中，刀具在切除金属的同时，其本身也逐渐被磨损。当磨损到一定程度时，刀具便失去切削能力，刀具磨损的快慢通过使用寿命也称刀具耐用度来衡量。当刀具磨损到磨钝标准仍继续使用时，会影响加工质量，降低生产率，增加成本［1］。所以，通过刀具使用寿命的合理选择，以及刀具在已累计工作t时间后能继续正常加工的时间（剩余使用寿命）的确定，是保证切削过程中加工质量的重要因素。

可靠性设计的方法是使用概率统计来求解，并通过失效概率的计算，定量地计算产品在工作中的可靠程度［2］。

本文采用洛必达方法对刀具剩余使用寿命的分析，进行切削过程中刀具可靠性研究，从而提高加工质量和可靠性，可避免由于刀具磨损造成的经济损失。

1 刀具使用寿命及耐用度

金属切削过程中，切削速度vc，进给量f，背吃刀量ap的选择与不同的工件材料对于刀具寿命都有不同程度的影响，由式（1）可得刀具使用寿命T的经验公式：

式中：m为切削速度的指数，与刀具材料有关；n为进给量的指数；p为背吃刀的指数；CT为工件材料和其他切削条件有关的系数［1］。

对于不同的工件材料和刀具材料，在不同的切削条件下，式（1）中的系数和指数可在有关资料中查出，所以此经验公式对于刀具使用有一定的预测作用。

式中，m、n、p、CT通过大量实验得到，具有随机变量的离散性质，所以对于根据式（1）得出的T，配合概率统计的方法进行刀具剩余寿命评估（刀具使用时间t后仍能正常使用的可靠度）。对于刀具剩余寿命本文洛必达方法进行分析和计算［3］。

2 金属切削刀具剩余寿命及其分布

设金属刀具使用寿命T为连续型正随机变量，分布函数为F（t）,其概率密度函数f（t）。假定刀具在切削过程中已积累使用过t时间，则由条件概率可求得剩余寿命的分布,记为：

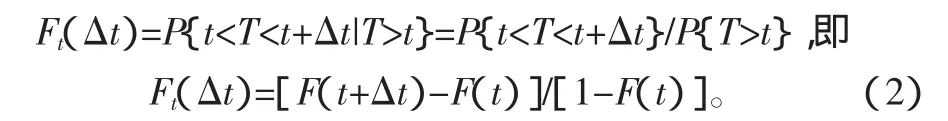
可见，金属切削刀具剩余寿命分布是初始寿命分布的截尾分布，所以其切削过程中的寿命分布实际上就是剩余寿命分布。记系统的剩余寿命为 u（t）［3］，则

式中，R（t）=1-F（t）为系统的可靠度函数。u（t）与失效率函数 λ（t）有以下关系：

3 金属切削刀具剩余寿命抽样的洛必达方法

金属切削刀具剩余寿命抽样的困难在于随着t的增大，F（t）≈1，关键问题是解决剩余寿命的抽样。设寿命分布具有概率密度函数f（t），当F（t）=1时，由求极限的洛必达法则，得到

式（7）是代数方程，不包含对时间的积分，很容易解出使用时间t后在经过Δt时间后可靠度u。

以正态分布函数N（μ，σ2）剩余分布抽样为例，使用时间t后在经过Δt时间后可靠度u。

式（8）为正态分布函数的概率密度函数［4］。

例如硬质合金刀具,其使用寿命服从参数μ=400 min，σ=60 min的正态分布，设该刀具已累积工作640 min，求该刀具在继续使用30 min内失效的概率。

解得，u=0.877。

4结语

从实际应用的角度讲,金属切削过程中刀具的使用寿命完全符合损耗型寿命分布，所以在刀具使用上可以结合刀具寿命的经验公式配合可靠性设计，提高加工过程中可靠性与经济性。在粗加工或者非关键尺寸的加工时可以适当延长使用时间，降低刀具成本，当精加工时采用较高的可靠度保证剩余使用寿命中刀具的可靠性。

［1］ 韩秋实.机械制造技术基础［M］.北京：机械工业出版社，1998.

［2］ 赵松年，佟杰新，卢秀春，等.现代设计方法［M］.北京：机械工业出版社，2011.

［3］ 张宏斌，王进才.直升机机载设备剩余寿命可靠性评估［J］.电子产品可靠性与环境试验，2006，24（1）：6-8.

［4］ 中国人民大学数学教研室.概率论与数理统计［M］.北京：中国人民大学出版社，1985.