基于背景值和初始值改进的灰色预测模型

刘俊峰，夏爱生，夏军剑

(军事交通学院基础部，天津300161)

GM(1，1)模型(灰色预测模型)［1］自 20 世纪80年代提出以来，由于其所具备的所需样本少、计算简单、可检验等特点，现已广泛应用于国民经济、工农业生产等各个领域，并成功解决了大量实际问题。但GM(1，1)模型本身存在一定的局限性，主要表现在两个方面:一是背景值的构造，由于发展系数a和灰色作用量b对模型的预测精度有深刻的影响，而a、b的取值与背景值的构造方法有关联，当a的预测值比较大时，传统的预测模型预测误差相对来说较大［2］;二是初始值的确定，传统的灰色预测对于参数C的处理方法是曲线X(1)(t)过点(1，X(1)(1))，代入通解可以解出 C值，这样做虽然可以使模型的计算过程简单，但由于最优的拟合曲线并不一定经过历史数据中的某一点，从而不能保证模拟序列和原始序列的最优拟合:这些因素导致了传统预测模型相对不稳定。基于这种情况，本文提出了一种改进的GM(1，1)模型，并结合实例进行预测。

1 灰色预测模型原理

令 X(0)为 n元序列，X(0)={X(0)(1)，X(0)(2)，…，X(0)(n)}，X(1)为 X(0)一次累加生成，X(1)={X(1)(1)，X(1)(2)，…，X(1)(n)}。

于是X(1)的GM(1，1)白化形式的微分方程为

假设拟合曲线X(1)(t)过累加序列的第一个点，即当t=1时，^X(1)(t)=X(1)(1)代入式(3)，离散化可得GM(1，1)的时间相应序列:

还原到原始序列可得灰色预测模型

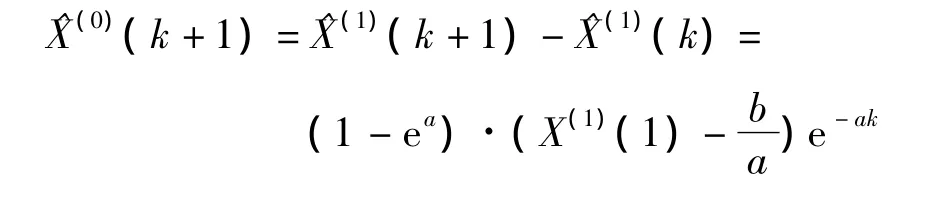
2GM(1，1)模型的改进

2.1 对背景值的改进

通过分析传统的GM(1，1)模型的建模过程，发现发展系数a和灰色作用量b对模型的预测精度有深刻影响，a、b的取值与背景值的构造方法有关联，传统的背景值Z(k)(t)dt=(k+1)+X(1)(k))。经过预测发现当a比较小时，预测的误差偏小;当a越大时，预测误差就越大。本文提出修改背景值的权值λ，即令

根据微分方程解的形式，可求出权值λ，并可进行多次迭代，以达到减小误差的目的。对式(1)在［k，k+1］上进行积分:

从上式可以看出，当a较小时，λ取1/2较合理，当a比较大时，λ取1/2会导致预测误差加大。

由式(4)可得

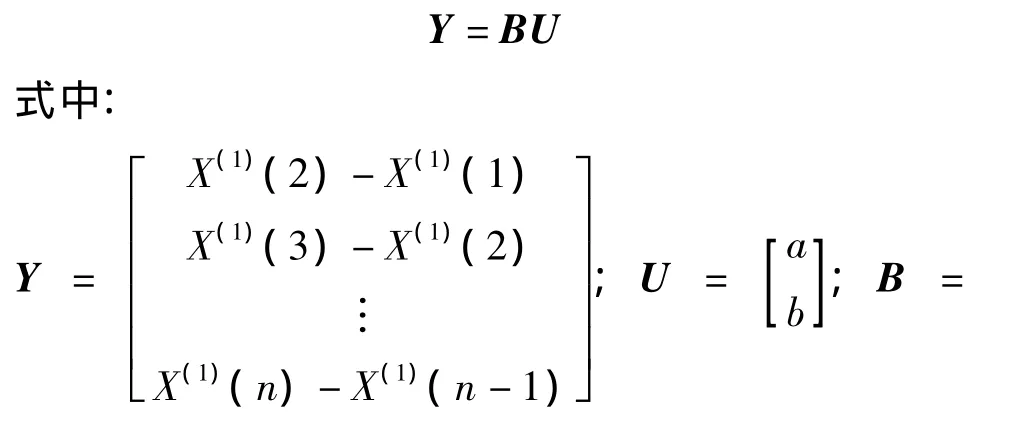
在预测过程中发现矩阵B中含有待估参数a的函数λ，这里赋初始值λ=1/2，进行最小二乘估计，得到a的一次估计值a1，把a1代入式(5)，改变矩阵B，重新进行最小二乘估计，得到a的二次估计值a2，可逐步进行下去得出a的最优值。

2.2 对初始值的改进

对于白化微分方程式(1)的通解为式(3)，传统的灰色预测对于参数C的处理方法是曲线X(1)(t)过(1，X(1)(1))点，代入通解可以解出 C值。这样做虽然可以使模型的计算过程简单，但由于没有对白化方程的时间响应函数进行优化，从而不能保证模拟序列和原始序列的最优拟合。因为最优的拟合曲线并不一定经过历史数据中的某一点。

针对GM(1，1)模型检验的一般方法，运用最小二乘法原理优化模型的时间响应函数，以X(1)序列的模拟值和X(1)序列的观测值的残差平方和最小为条件［3-4］，确定时间响应函数中的常数C，从而建立起相应的最优时间响应函数，大大提高了模型的预测精度。

(1)白化微分方程=b的解亦称时间响应函数，表达式为

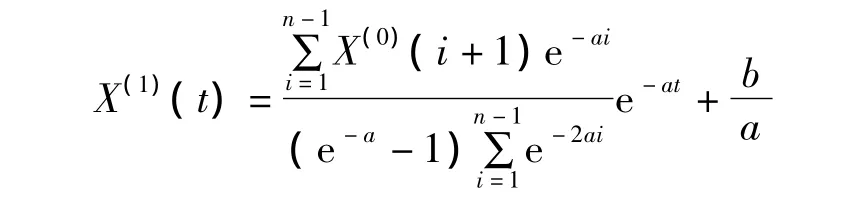
(2)灰色微分方程X(0)(t)+aZ(t)=b的时间相应序列为

证明

为了求C，利用最小二乘原理，构造X(0)序列的模拟值和X(0)序列的观测值的残差平方和函数:

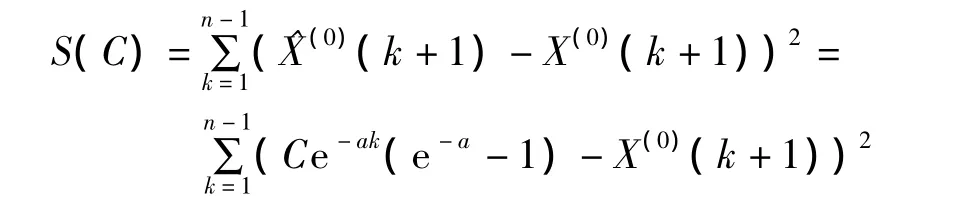
求C使得S(C)达到最小。令S'(C)=0，求得唯一驻点:

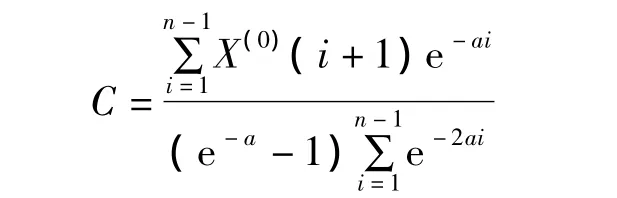
根据问题的实际情况，得知残差平方和S(C)在此驻点处取最小，故

(2)令 t=k+1，可以得到灰色微分方程X(0)(t)+aZ(t)=b的时间相应序列为

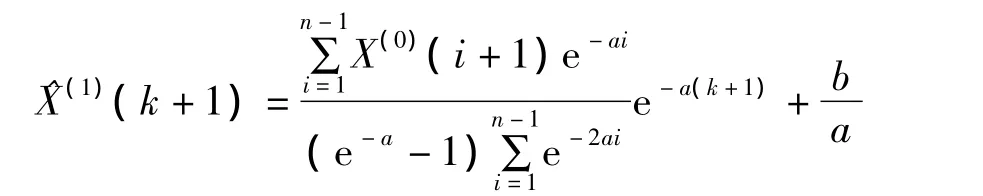
(3)对X(1)累减后化简可还原原始数据。

3 实例分析与对比

为检验改进模型的性能，以文献［5］中2003—2011年我国原煤总产量实测数据为例(见表1)，建立本文改进的GM(1，1)模型，对2009—2011年原煤总产量进行预测，并与文献［5］中预测数据进行对比(见表2)。具体步骤:

(1)对原始序列进行累加处理，得到它的累加生成序列;

(2)利用经典模型预测初值，代入式(5)，利用式(6)进行预测;

(3)把预测出来的值再次代入式(5)，利用式(6)进行预测，得出时间相应式(1)的具体形式;

(4)把C值代入式(1)中预测出2009年的原煤总产量，并把预测值加入到原序列，重复以上步骤，直至把2009—2011年原煤总产量都被预测出来。

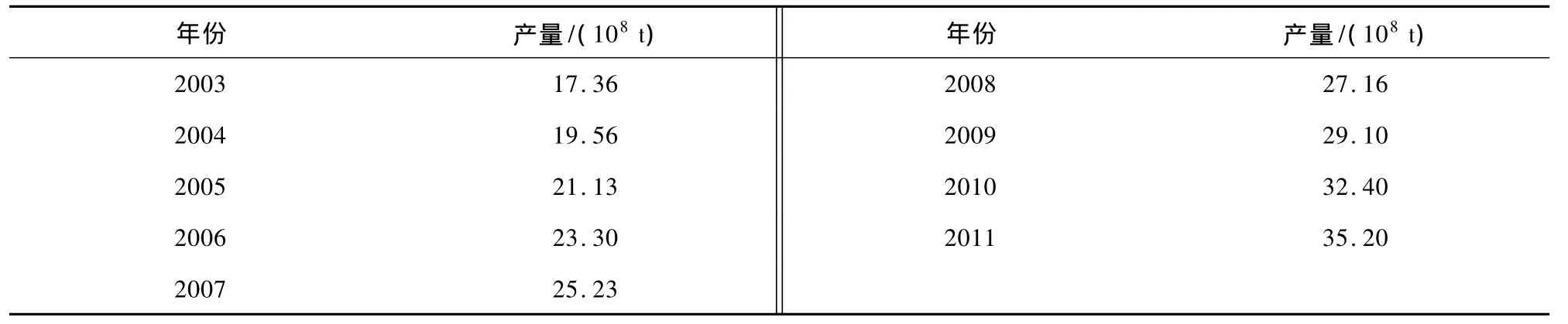
表1 2003—2011年我国原煤总产量

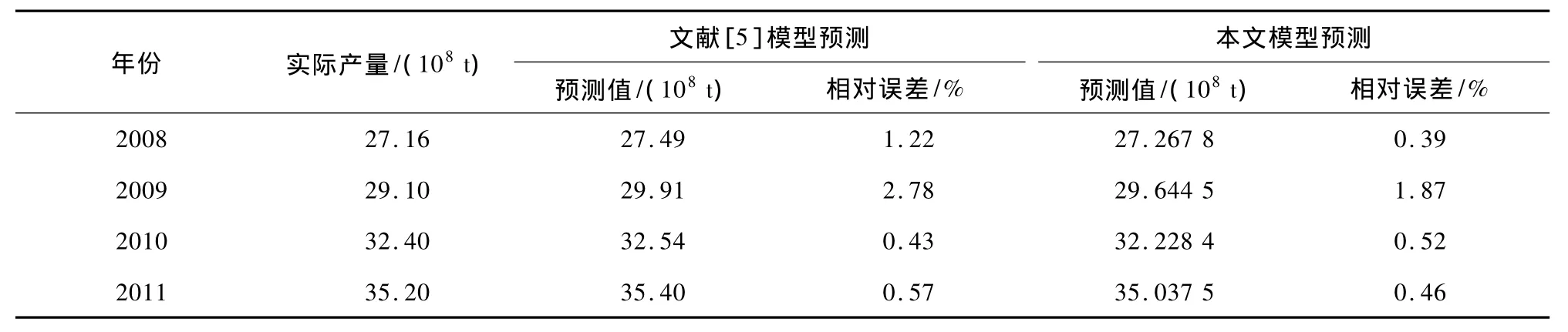
表2 2008—2011年我国原煤总产量预测值与相对误差值对比

由表2可以看出，2008—2011年文献［5］模型预测结果的平均误差为1.25%;本文改进的GM(1，1)模型预测结果的平均误差为0.81%，而2003—2011年本文预测结果的平均误差为0.683%。可见本文改进的预测模型精度有了明显的提高。

4 结语

在传统的GM(1，1)模型中通常将背景值取为相邻两个数的算术平均值，对于不同的数据势必导致误差的精度不同，当a比较大时，预测的误差较大。另外，直接将 ^X(1)(1)=X(1)(1)作为已知条件，求解模型的时间响应函数，这些都导致得出的预测数据精度不高。本文首先对背景值进行加权处理，从而得到精度较高的权值，同时根据最小二乘原理确定时间响应函数中的常数C，建立起相应的最优时间响应函数，并通过实例表明，改进的模型可以提高预测精度。

［1］ 邓聚龙.灰色系统［M］.北京:国防工业出版社，1985:1-25.

［2］ 王叶梅，党耀国，王正新.非等间距GM(1，1)模型背景值的优化［J］.中国管理科学，2008，16(4):159-161.

［3］ 王健.一类改进的灰色预测模型及其应用［J］.数学的实践与认识，2013，43(9):181-185.

［4］ 陈友军，何洪英.利用非线性规划方法最优化灰色预测模型［J］.计算机工程与应用，2014，50(10):61-63.

［5］ 罗迪，马新.基于Gauss－Legendre公式改进的煤炭产量灰色预测模型研究［J］.煤炭工程，2014，46(4):90-93.