利用GNSS水准实现跨河高程传递的方法及精度分析
张兴福,张永毅
利用GNSS水准实现跨河高程传递的方法及精度分析
张兴福,张永毅
(广东工业大学 测绘工程系,广州 510006)
针对国家一、二等水准测量规范(2006)对利用GNSS水准技术实现跨河高程传递的要求展开研究,本文采用规范方法和基于移去恢复技术的高差拟合法对利用GNSS水准实现二等跨河高程传递进行有关实验,实验结果表明:在海拔较低(小于500 m),且高程异常变化平缓的测区,按照规范较容易达到二等水准测量精度要求,而对于海拔较高,且高程异常变化较大测区,虽然规范不建议进行GNSS跨河水准测量,但采取基于移去恢复技术的高差拟合法同样可以达到二等水准测量要求。
GNSS水准;跨河;高程传递;精度分析
0 引言
常用的跨河高程传递方法有:光学测微法、倾斜螺旋法、三角高程法以及全球卫星导航系统(global navigation satellite system,GNSS)水准法[1-8],光学测微法是使用一台水准仪并配备专用的照准觇板进行跨河高程传递,最长跨距小于500 m;倾斜螺旋法也是常用的跨河高程传递的方法之一,需要使用2台水准仪对向观测,用倾斜螺旋来测定水平视线两标志的倾角,从而求出两岸高差,跨距不超过1 500 m;随着测量机器人技术的发展,三角高程法备受关注,大量实验结果表明该方法可达到很高的精度,但需要对向同步观测,跨距不超过3 500 m;GNSS水准法由于方法简便,工作量较少,也广泛用于跨河高程传递,跨距不超过3 500 m。在这4种方法中,GNSS水准法受外业观测条件影响较小,其它3种方法受外业观测条件影响较大[9]。
本文主要探讨GNSS水准法用于跨河高程传递的方法与精度分析,并对2个项目跨河高程传递进行了分析,获得的结论对采用GNSS技术进行跨河高程传递有较好的参考价值。
1 原理与方法
1.1 由高程异常变化率直接计算正常高差
GNSS跨河水准测量应选择在地形较为平坦的平原、丘陵且两岸地貌形态基本一致的地区进行,且海拔高不宜超过500 m,当地形起伏超过130 m/km时不宜进行二等跨河水准测量,并尽量使得跨河点和非跨河点在同一条直线上。GNSS跨河水准测量工作示意图见图1,其中A1、A2、D1和D2为非跨河点,而 B和C为跨河点[9]。

图1 GNSS跨河水准工作示意图
地面上任意i,j两点间的高程异常变化率可写为
αij=(ΔHij-Δhij)/Sij
(1)
式(1)中,αij为ij方向的高程异常变化率,单位为m/km;Sij为i、j点间的平距,单位为km;ΔHij为i、j点间的大地高差,单位为m;Δhij为i、j点间的正常高高差,单位为m。
根据式(1)由每一个非跨河点与最近跨河点计算得到一个α值,最后将河流两岸得到的不同的αAB与αCD取平均值作为跨河河段的高程异常变化率αBC,见图1。河流两岸得到的不同的α值较差应满足表1中的有关规定。

表1 高程异常变化率限差表/(m·km-1)
跨河线路BC之间的跨河水准高差可由下式计算:
ΔhBC=ΔHBC-αBC×SBC=ΔHBC-ΔζBC
(2)
式(2)中,ΔhBC为待求的BC间的正常高差,单位为m;ΔHBC为BC间的大地高差,单位为m;αBC为BC方向的高程异常变化率,单位为m/km;SBC为BC点间的平距,单位为km;ΔζBC为BC点间的高程异常差,单位为m。
1.2 高差拟合计算
区域大地水准面变化的不规则性使得不同GNSS水准点之间的高程异常差变化率存在差异,当这种差异小于规范要求时,利用规范很容易达到设计精度要求,但当这种差异超出规范要求时,我们将分析采用高差拟合方法能否达到设计精度要求。结合规范要求跨河控制点必须布置在同一条直线上,为了提高高差拟合精度,并简化拟合模型,需建立跨河线路独立坐标系。
1.2.1 跨河线路坐标系的建立
以某一跨河点或非跨河点作为独立坐标系坐标原点o′,以跨河点连线的延伸方向作为x′,过坐标原点o′且与x′轴垂直方向为y′轴,建立跨河线路坐标系[10],如图2所示。由于跨河点与非跨河点基本沿x′轴分布,故可以忽略y′轴方向高程异常的变化,而仅考虑沿跨河方向的高程异常变化,常用的拟合模型有直线、二次曲线及三次曲线等[11-12]。
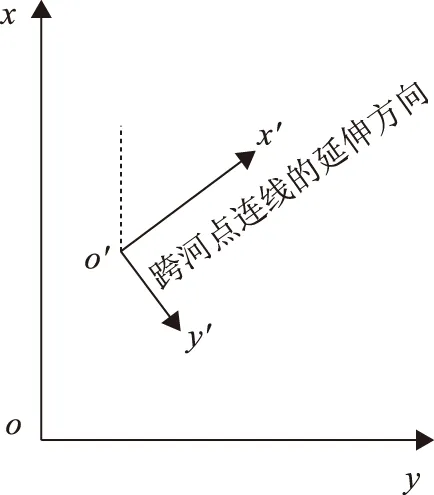
图2 跨河线路坐标系示意图
1.2.2 拟合模型
三次曲线GNSS高程拟合的计算公式为:
ζ=a0+a1x+a2x2+a3x3
(3)
由于在GNSS跨河高程传递中,两岸水准测量仅能获得同岸控制点间的正常高差,故高程拟合并不适用,式(3)可改为高差拟合模型,即:
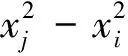
(4)
式(4)中,ai为拟合系数,Δζij为i,j两点间的高程异常差,进行三次曲线拟合至少需要3段高差,式(4)中,若只考虑右式第1项,则式(4)退化为直线拟合模型,若只考虑前2项,则式(4)为二次曲线拟合模型。
利用式(4)建立高差拟合模型后,即可求取两跨河点间的正常高差,由于规范要求跨河两端各需要3个控制点,故可以进行三次曲线拟合。
2 结果与精度分析
2.1 松花江高程传递实验及精度分析
跨河实验1为跨越松花江的某条客运专线,高程传递距离约1 km,测区平均海拔118 m,见图3,其中SHJ3和SHJ4为两个跨河点,SHJ1、SHJ2、SHJ5和SHJ6为非跨河点,点号自北向南依次排列,点间高差采用二等水准联测,大地高差采用GNSS技术获得,观测时间为2 h,共4个时段,平差后大地高精度优于5 mm。
按照规范计算方法计算结果见表2,其中3-4段结果中,除大地高差为观测值外,其余结果均为计算结果,表2结果显示,同岸高程异常变化率和不同岸高程异常变化率均不超过表1中的有关规定,算得跨河点间的高程异常变化率为0.028 995 m/km,高程异常差为0.029 0 m,从而算得跨河点间正常高差为2.178 6 m,由于各项指标均满足规范要求,故我们认为本次实验结果满足二等水准测量要求。为了进一步对该结果进行分析和检核,我们采用简单直线拟合法,即以SHJ1到SHJ2、SHJ2到SHJ3、SHJ4到SHJ5及SHJ5到SHJ6的正常高差及大地高差为已知数据来拟合SHJ3到SHJ4跨河段的正常高差,拟合结果为2.179 2 m,与规范方法计算结果仅相差0.6 mm,两者的计算结果是一致的。
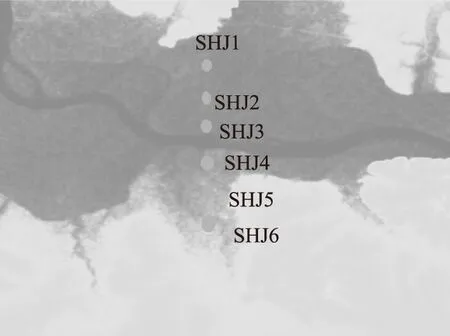
图3 跨河实验1点位示意图

图4 跨河实验2点位示意图
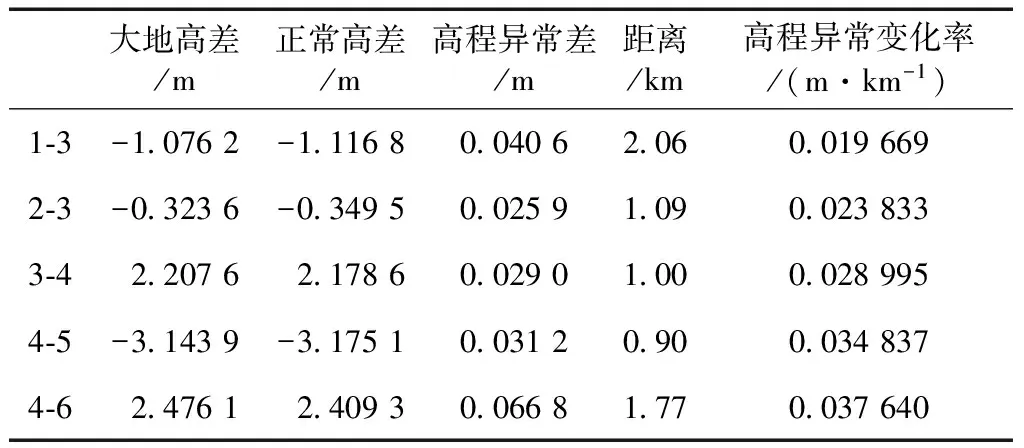
大地高差/m正常高差/m高程异常差/m距离/km高程异常变化率/(m·km-1)1⁃3-10762-111680040620600196692⁃3-03236-034950025910900238333⁃422076217860029010000289954⁃5-31439-317510031209000348374⁃62476124093006681770037640
2.2 黄河高程传递实验及精度分析
跨河实验2为跨越黄河的某条客运专线,高程传递距离约0.7 km,测区平均海拔970 m,见图4,其中hh3和hh4为两个跨河点,hh1、hh2、hh5和hh6为非跨河点,点号自北向南依次排列,点间高差采用二等水准联测,大地高差采用GNSS技术获得,观测时间为4 h,共6个时段,平差后大地高精度也优于5 mm。由于该测区平均海拔超过500 m,故规范不建议进行二等GNSS跨河高程传递,为了更好地对本文结果进行分析,采用常规二等水准通过附近桥梁联测了跨河点间的正常高差,以用作结果比较。
按照规范计算方法计算结果见表3,其中3-4段结果中,除大地高差为观测值外,其余结果均为计算结果,表3结果显示,北岸控制点间高程异常变化率差异略微超过了规范要求,而南岸控制点间高程异常变化率差异超过了规范要求,故按照规范要求本次联测即使大地高精度很高,也无法满足二等水准精度,若按照规范方法计算跨河点间正常高差,则结果为3.572 4 m,而通过水准联测的两点的正常高差为3.590 7 m,差值为18.3 mm,远远超过了二等水准测量的限差要求(跨河段二等限差要求为3.2 mm)。

表3 实验2高差计算结果
为了进一步分析拟合方法是否可以达到二等水准测量精度要求,现采用直线、二次曲线、三次曲线拟合方法对跨河段的高差进行拟合,即以hh1到hh2、hh2到hh3、hh4到hh5及hh5到hh6的正常高差及大地高差为已知数据来拟合hh3到hh4跨河段的正常高差,拟合结果与水准测量结果差值分别为12.4 mm、12.4 mm和13.2 mm,均超过了二等水准测量的限差要求。基于2 190阶的EIGEN-6c4重力场模型,采用移去-恢复法重新进行拟合[12-13],则三种方法获得的正常高差与实测结果的差值分别为4.2 mm、4.2 mm和2.4 mm,可以说明,基于2 190阶的EIGEN-6c4重力场模型的移去-恢复法能显著提高跨河段高差拟合精度,其中三次曲线拟合精度能满足二等水准测量的精度要求。
3 结束语
本文采用两个客运专线的GNSS水准数据对跨河高程传递进行研究,获得结论如下:
(1)严格按照规范要求采用GNSS水准技术可以达到二等跨河水准的精度要求。另外可以采用高差拟合方法对规范计算方法进行检核,为了更好地进行拟合,并简化拟合模型,可以考虑建立跨河独立坐标系,以忽略垂直线路方向的高程异常变化。
(2)在海拔较高的测区,规范计算方法无法达到精度要求,可以考虑采用基于移去-恢复技术的三次曲线拟合方法,参考模型可以选择2 190阶的EIGEN-6c4重力场模型。
[1] DENG Xing-sheng,HUA Xiang-hong,YOU Yang-sheng.Transfer of Height Datum Across Seas Using GPS Leveling,Gravimetric Geoid and Corrections Based on a Polynomial Surface[J].Computers & Geosciences,2013,51(2):135-142.
[2] LI Jian-cheng,JIANG Wei-ping.Long Distance Transference of Height Datum Across Seas[J].Geo-spatial Information Science,2002,5(3):1-5.
[3] 陈功亮,赵峰.跨海大桥的三种高程控制测量方法[J].测绘通报,2008(12):42-44.
[4] 林明华,苏志坚,侯飞.精密三角高程测量用于跨河高程传递的实验研究[J].测绘科学学,2012,37(5):209-211.
[5] 时学军.二等跨河水准测量在狮子洋水下隧道工程测量中的应用[J].铁道勘察,2007,33(5):39-40.
[6] 郭建东,陈红权,朱小毛,等.南京长江二桥跨河精密高程控制测量[J].测绘工程,2006,15(3):38-41.
[7] 胡兴树,欧小善,李伟,等.琼州海峡精密高程传递方法研究与试验[J].测绘通报,2012(增刊1):154-158.
[8] 熊伟,吴迪军,李剑坤.GPS在桥梁跨河水准测量中的应用研究[J].测绘科学,2012,37(2):100-102.
[9] GB/T 12897-2006,国家一、二等水准测量规范[S].北京:中国标准出版社,2006.
[10]谭衍涛,张兴福,王兵海,等.利用 GNSS /水准实现长大隧道群高程传递的方法研究[J].测绘通报,2015(3):61-65.
[11]郭春喜,聂建亮,王斌,等.区域似大地水准面拟合方法及适用性分析[J].大地测量与地球动力学,2013,33(1):103-107.
[12]张兴福,刘成.综合EGM2008模型和SRTM/DTM2006.0剩余地形模型的 GPS高程转换方法[J].测绘学报,2012,41(1):25-32.
[13]张兴福,李博峰,魏德宏,等.多类重力场模型的精度分析及联合确定GPS点正常高的方法[J].测绘学报,2013,42(1):6-12.
The Method and Accuracy Analysis of River-crossing Leveling Based on GNSS Leveling
ZHANGXing-fu,ZHANGYong-yi
(Department of Surveying and Mapping,Guangdong University of Technology,Guangzhou 510006,China)
The requirements of river-crossing leveling based on GNSS leveling are investigated according to specifications for the first and second order leveling(2006),the experiments of second order river-crossing leveling are carried out using standard method and level difference fitting method based on remove-restore technology,the results show that the second order leveling can be achieved according to the specifications at the lower altitude (less than 500m)and smooth height anomaly area,and for high altitude and height anomaly changes larger area,although the GNSS river-crossing leveling is not recommended in specifications,but if level difference fitting method based on remove-restore technology can be adopted,the second order leveling can also be achieved.
GNSS leveling;River-crossing;Height transfer;Accuracy analysis
张兴福,张永毅.利用GNSS水准实现跨河高程传递的方法及精度分析[J].导航定位学报,2015,3(3):135-138.(ZHANG Xing-fu,ZHANG Yong-yi.The Method and Accuracy Analysis of River-crossing Leveling Based on GNSS Leveling[J].Journal of Navigation and Positioning,2015,3(3):135-138.)
10.16547/j.cnki.10-1096.20150327.
2015-05-18
国家自然科学基金(41104002),地球空间环境与大地测量教育部重点实验室开放基金(10-01-07)。
张兴福(1977—),山东临沂人,副教授,主要从事卫星重力及GNSS数据处理等。
P228
A
2095-4999(2015)-03-0135-04

