PWM整流器基于虚拟磁链的新型直接功率协调控制研究

朱鹏程，黄文新

（南京航空航天大学自动化学院，江苏 南京210016）

0 引言

PWM整流器具有越来越好的发展前景，其性能要求也越来越严，这就对PWM整流器的控制技术提出了更高的要求［1］。

近年来，直接功率控制以其控制算法简单，动态响应快等优点得到了许多学者的关注。传统的直接功率控制采用滞环控制，它的优点是控制算法简单，但具有开关频率不固定，采样频率要求高等缺点［2－3］。为了解决这个问题，近年来国内外一些学者提出一种恒频直接功率控制策略［4］，它主要根据功率误差和电网电压电流计算出交流侧输入电压，简化了系统结构。传统PWM整流器控制大多数采用单独控制，这使得母线电容很大。另外，当负载突变时，系统控制性能恶化。针对这种情况，很多学者提出了协调控制策略［5－8］。

在此，提出了一种新型PWM整流器控制策略。该策略先将负载功率前馈到电容功率后得到有功功率，然后利用功率误差和电网电流计算产生整流器参考电压，经过SVPWM调制得到驱动信号，从而在功率内环省去了PI调节器，简化了系统结构。另外，该控制利用开关信号、直流母线电压和交流电流计算虚拟磁链，从而省去电网电压传感器，降低了硬件成本的同时又提高了系统的可靠性。最后，通过仿真和实验，证明了该控制策略的可行性和优越性。

1 三相PWM整流器数学模型

三相PWM整流器主电路结构如图1所示。

在图1中，ea，eb，ec为电网电压；ia，ib，ic为交流侧相电流；ua，ub，uc为整流器相电压；udc为直流母线电压。

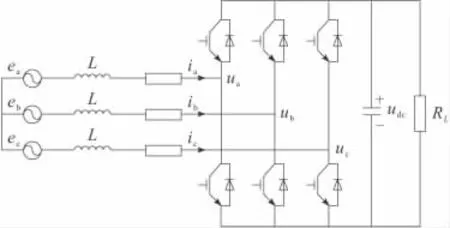
图1 三相PWM整流器主电路结构

设三相电网电压平衡，则可得到在dq坐标系中，三相PWM整流器的数学模型：

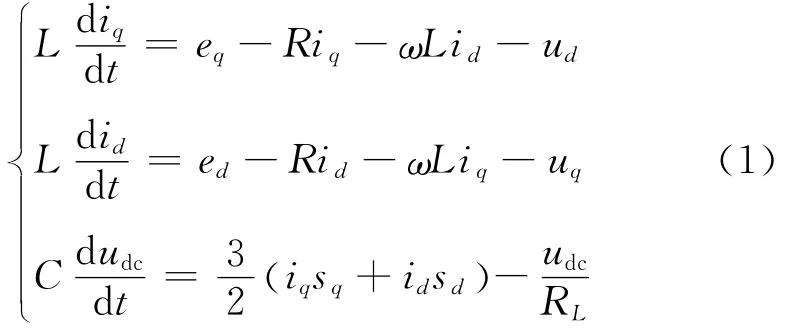
R，L为交流侧输入电感的电阻和电感值；sd，sq为开关信号在dq轴上的分量。根据瞬时功率原理，系统瞬时有功和无功功率在αβ坐标系可表示为：

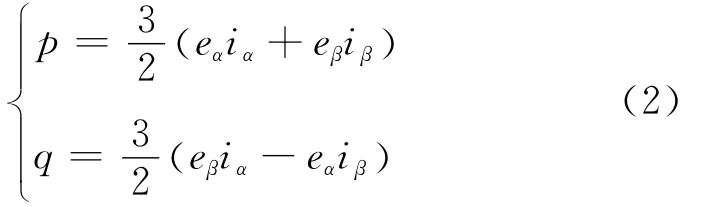
通过坐标变换，可以得到在dq坐标系中瞬时有功和无功功率的表达式：

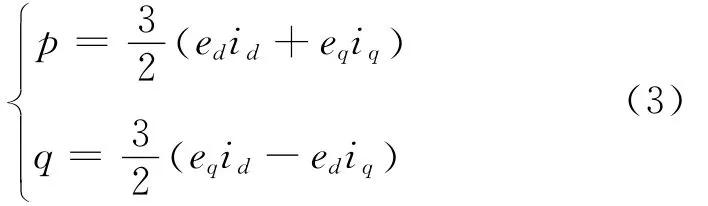
在直流侧，母线上电容功率为：

若忽略整流器的损耗，可以得到网侧瞬时有功功率流动的表达式为：

由虚拟磁链的概念，可得虚拟磁链αβ分量为：

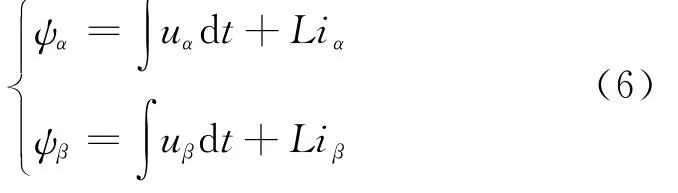
uα，uβ为整流器电压，可用直流侧电压udc和开关信号Sa，Sb，Sc表示为：

从式（6）～式（7）可知，通过检测直流电压、开关信号及三相交流电流，就可以得出虚拟磁链，进而计算出瞬时功率，从而省去电网电压传感器。

2 基于虚拟磁链的直接功率协调控制策略

根据磁链和电压的关系，可得：

将虚拟磁链定向于dq坐标系的d轴上，有ψq＝0，ψd为常量，那么可得：

因为ψd为常量，因此有ed＝0。将式（9）代入式（3），可得：

对式（10）两边进行求导，可以得到：

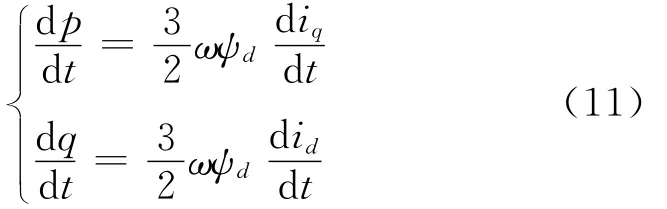
将式（1）前2个公式和式（9）代入式（11），并在单个采样周期内将之离散化可得：

Ts为系统采样周期。

由式（12）可以得到在dq坐标系中下个周期整流器参考电压表达式为：

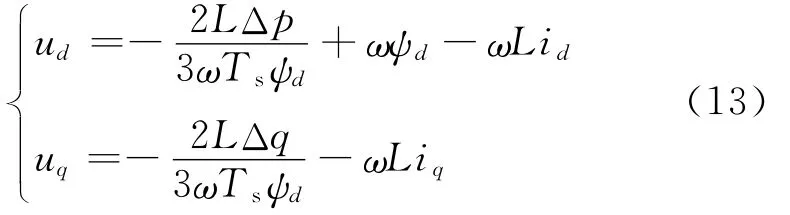
由式（13）可知，通过功率误差、虚拟磁链和电网电流，可以计算出整流器参考电压。从而省略了PI调节器，降低了控制系统的复杂性。

设瞬时有功功率和无功功率参考值为p＊和q＊，则在每个离散周期内系统功率参考值和实际值之间的误差为：

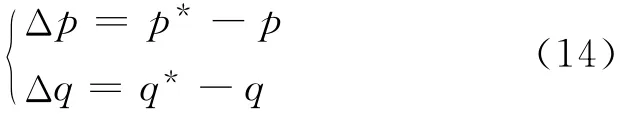
由式（5）可知，p＊是电容功率和负载功率相加得到，因此有功功率参考值p＊要分成电容功率和负载功率2项分别计算。

设uD＝，则对于式（4）整理得：

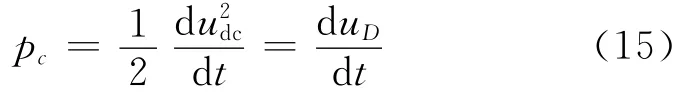
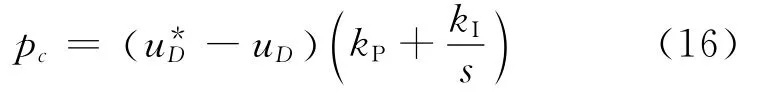
根据式（5），电容侧功率pc加上负载功率pload得到有功功率参考值p＊，具体框图如图2所示。

写成PI控制器形式为：

3 整体控制结构

整体控制结构如图3所示。控制系统首先采样三相输入电流，通过开关信号、母线电压和交流电流计算出虚拟磁链和角度，得出瞬时有功和无功功率；通过电压外环得到有功功率参考值，计算出整流器参考电压；最后经坐标反变换输入到SVPWM调制后输出。

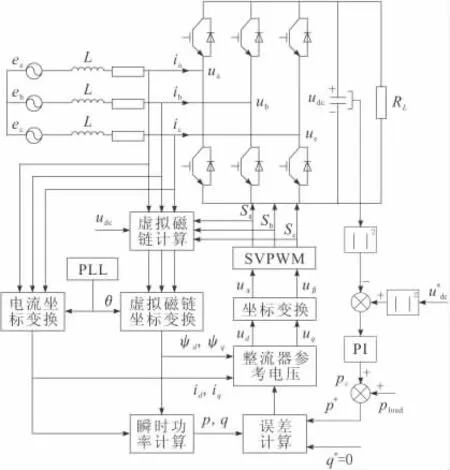
图3 整体控制结构

4 仿真与实验

4.1 仿真分析

在Matlab／Simulink里搭建仿真模型，对本文提出的控制策略进行验证，并在负载突变时对传统控制策略和新型控制策略进行比较。系统的主要仿真参数如表1所示。

表1 仿真参数

PWM整流器负载设为RL感性负载，负载电阻R＝80Ω，电感L＝8mH。从图4可以看出，PWM整流器可近似在单位功率因数下运行，直流电压输出稳定，电网侧电流正弦程度较好，谐波较少，证明了本文所提控制策略的可行性。

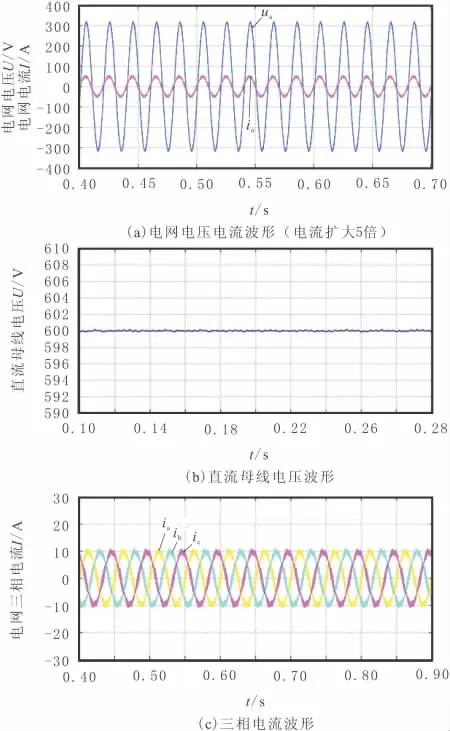
图4 系统仿真波形

负载增大1倍时，在传统控制策略和新型控制策略下，PWM整流器的直流母线电压对比如图5所示。从图5可以看出，当负载突变时，采用新型控制策略的直流母线电压脉动比采用独立控制策略的脉动大幅减少，并且响应速度更加快速。还通过实验得知，采用新型控制策略的电网电流THD含量更小，可知电网电流正弦化程度更高，谐波含量更少。这证明了新型控制策略的优越性。

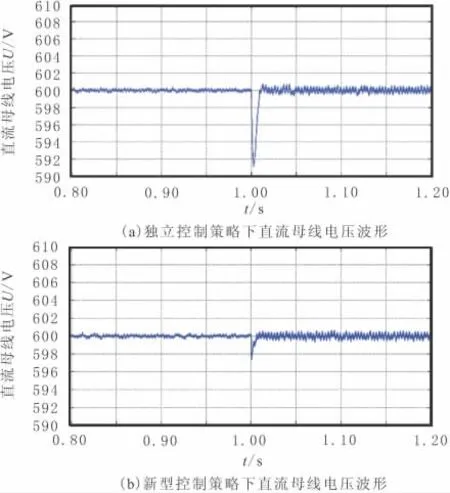
图5 直流母线电压对比

4.2 实验结果分析

为验证控制策略的有效性和优越性，搭建了硬件平台进行实验验证。系统采用飞思卡尔公司的基于增强型56800E内核的MC56F8346控制芯片作为核心控制器，实验主要参数如表2所示。

表2 实验参数

从图6～图8可以看出，PWM整流器可近似在单位功率因数下运行。电网侧电流正弦化程度较好，谐波含量较少。实验结果和仿真一致，证明了该策略的可行性。

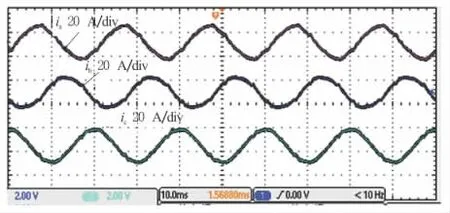
图6 三相电流实验波形

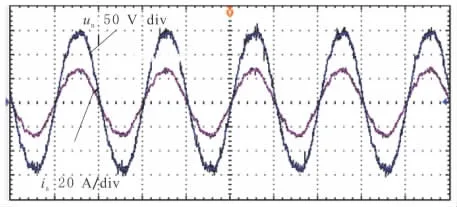
图7 A相电压电流实验波形

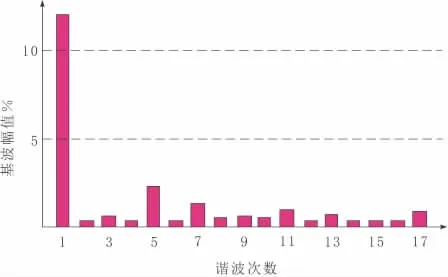
图8 A相电流频谱

图9 是负载突变（增大1倍）时，采用2种控制策略下的直流电压变化对比图。可以看出，在相同的负载波动下，采用新型控制策略的直流电压振荡幅度更小，响应更加快速。

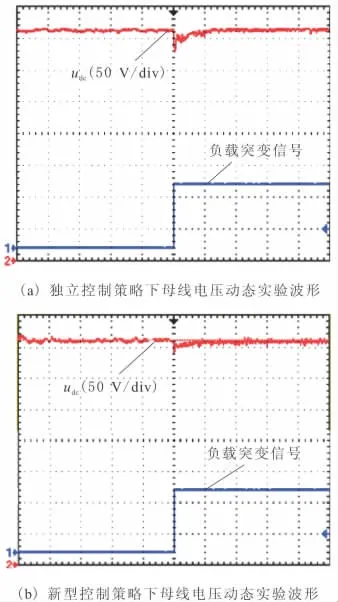
图9 2种策略下直流母线电压实验对比

5 结束语

提出了一种PWM整流器新型协调控制策略。介绍了PWM整流器数学模型，通过详细的公式推导得出控制策略，给出整体控制框图，并通过仿真和实验验证了可行性。该控制策略可有效抑制在负载突变时直流电压的波动，提高系统动态性能。另外，该控制不需要多个PI调节器进行控制，控制较为简单。最后，通过计算虚拟磁链，可省去电网电压传感器，降低硬件成本，提高系统稳定性。

［1］ 杨勇，吴国祥，谢门喜.基于滤波电感在线估算的并网逆变器直接功率预测控制［J］.电力系统保护与控制，2011，39（12）：84-89.

［2］ 程启明，程尹曼，薛阳.三相电压源型PWM 整流器控制方法的发展综述［J］.电力系统保护与控制，2012，40（3）：145-155.

［3］ 丁奇，严东超，曹启蒙.三相电压型PWM整流器控制系统设计方法的研究［J］.电力系统保护与控制，2009，37（23）：84-87.

［4］ 耿强，夏长亮，阎彦，等.电网电压不平衡情况下PWM整流器恒频直接功率控制［J］.中国电机工程学报，2010，30（36）：79-85.

［5］ Gu B G，Nam K.A DC link capacitor minimization method through direct capacitor current control［J］.IEEE Transactions on Industry Applications，2006，42（2）：573-581.

［6］ 王久和，杨微，李华德.功率前馈电压型PWM 整流器直接功率解耦控制［J］.辽宁工程技术大学学报，2007，26（2）：238-241.

［7］ 黄守道，陈继华，张铁军.电压型PWM 整流器负载电流前馈控制策略研究［J］.电力电子技术，2005，39（4）：53-55，62.

［8］ 李明水.双PWM变换器负载功率前馈直接功率控制［D］.天津：天津大学，2011.