TX1600G数控镗铣加工中心滚珠丝杠热特性分析

孙 军，秦显军，钱彬彬，黄 圆

（沈阳建筑大学机械工程学院，辽宁 沈阳110168）

0 引言

滚珠丝杠具有传动精度高、传动效率高、传动精度高、传动可逆性、同步性好和使用寿命长等优点，被广泛用于数控机床及加工中心。但是其热变形严重影响机床的加工精度［1］。为了保证机床的加工精度，需要对滚珠丝杠进行热误差补偿。利用ANSYS对在实际工况下的滚珠丝杠进给系统进行热仿真分析，为滚珠丝杠进给系统建立热误差补偿模型，提供理论依据。国内外已对滚珠丝杠进给系统热分析进行很多相关的研究。如美国佛罗里达大学的Ziegert［2］等用人工神经网络（ANN）方法，在一个双轴数控车床上建立了运动误差模型去预测误差的大小，并通过实验验证结果，表明神经网络能够较好预测误差，显著降低零件的尺寸误差。易学平［3］对丝杠机构在工作过程中，摩擦引起的温升和热变形进行分析，得出了适用于实际工况的温度场经验公式。何震［4］以滚珠丝杠进给系统的有限元热分析结果，建立了三维温度场数学模型，分析了进给系统的内部热源，确定有限元分析的边界条件，对温度场进行ANSYS仿真。夏军勇［5］等通过研究滚珠丝杠受周期变化热源影响而产生的温度场、热变形及其变化特性，进行理论分析和仿真，并用叠加法求解了多变化热源下的温度场函数，进一步为研究机床的热动态特性提供了理论基础。

1 滚珠丝杠进给系统热分析模型

在滚珠丝杠进给系统中，电机产生的热量要通过电机架和联轴器才能传递到滚珠丝杠上；工作台在导轨长度方向的摩擦力很小，产热不多；切削产生的热量及时被切削屑和冷却液带走，这些热量在分析过程中都可以忽略。因此进给系统的主要热源是轴承、螺母和滚珠丝杠旋转时的摩擦发热。

1.1 滚珠丝杠导热的理论模型

丝杠工作过程中没内热源，靠摩擦生热。当进给系统的热量流入和流出相等时，系统的温度不再随着时间变化，此时系统进入热平衡状态［6］。由于机床上的丝杠长径比很大，为了方便以后的研究，忽略径向的温度变化，而且丝杠是轴对称的，所以将进给系统丝杠轴的传热模型简化成一维传热模型。满足热传导微分方程：

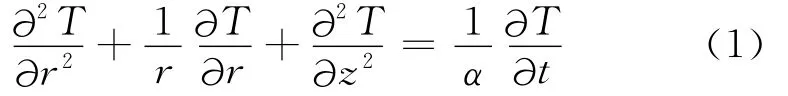
丝杠温度分布初始条件为：

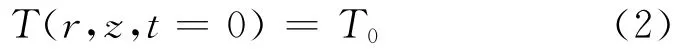
T0为初始温度，丝杠与工作环境的初始温度设定为20℃。

1.2 发热量的计算及边界条件的确定

根据传热学理论［7］，辐射散热的热量较少，故一般只考虑热传导和热对流。滚珠丝杠副的热源包括摩擦热、环境温度和热辐射等，但主要是摩擦热，摩擦发生在丝杠与支承轴承、螺母之间。为了确定热源强度，需要计算摩擦力矩，根据摩擦力矩再计算热流密度参数。

1.2.1 发热量分析

轴承的发热量主要是由轴承的摩擦力矩引起的，其发热量为［8］：

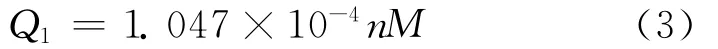
发热量Q是无法直接加载到有限元模型上，必须转换成热流密度形式，其计算公式为：

S为热源面积。

1.2.2 丝杠轴与螺母的热源分析

丝杠与螺母之间的摩擦主要通过滚珠与滚道面的接触摩擦。滚珠和滚珠面近似看作点接触，摩擦是发生在滚道面上的局部区域，而非整个滚道面。

丝杠轴与螺母的摩擦引起螺母发热，其发热量为：

Qlm为丝杠轴与螺母间的发热量；n为丝杠的转速；M为丝杠与螺母间的摩擦力矩。

由于丝杠轴与螺母间的摩擦热量分配于滚珠、螺母和丝杠轴，其中摩擦热量43%是经过滚道面传导到丝杠轴上，那么热流密度q2为：

1.2.3 滚珠丝杠副的对流换热

流体与滚珠丝杠副表面接触时，会发生热量交换，这是滚珠丝杠副主要的散热方式。流动介质流动起因主要分为2大类，其一是由于流动内部密度差引起的，如丝杠停止运转且空气流转时空气冷却，称其为自然对流换热；其二是由于外部动力源所造成的，如冷却介质流经中空丝杠的孔道，称为强制对流换热。

分析对流换热系数的众多影响因素，根据相似性分别分成若干个无量纲参数，然后通过实验确定这些相似性间的关系，即准则公式。根据上述方法，可获得所有对流换热的努谢尔特准则：

Nu为努谢尔特数；k为流体的热传导系数；L为特征长度。

滚珠丝杠高速旋转，则会带动周围的空气加速运动，从而形成强迫对流换热h1。所以丝杠滚道面的努谢尔特准则为：

Re为空气的雷诺系数；ω为丝杠轴的角速度；d0为丝杠轴的公称直径。

对于管内湍流强制对流换热系数h2，常采用以下表达式：

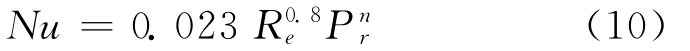
2 滚珠丝杠副有限元模型

2.1 滚珠丝杠副建模及网格划分

由图1可知，滚珠丝杠高速旋转，导致丝杠螺母、支持轴承与丝杠摩擦产生大量的热，引起热变形，降低传动与定位精度，特别是在高速运转的情况下丝杠系统有可能产生噪声和震颤。

图1 TX1600G数控机床镗铣加工中心

如果将模型全部导入ANSYS中，则影响建模速度，增大计算量，影响计算精度。所以应简化模型，在发热量不变的条件下，用等直径的光杆圆柱体来代替丝杠轴，轴承和螺母则用等直径的空心圆柱体来简化。利用UG建立三维实体模，将三维模型导入ANSYS中。

选择单元SOLID90划分网格。采用具有热结构CONTA174和TARAE170，来模拟滚珠丝杠副中丝杠与螺母及轴承之间的热传导。因为丝杠具有不规则性，所以采用自由法划分网格。

2.2 滚珠丝杠副的移动热载荷［9］

机床在空载进给时，螺母在丝杠上往复移动，为了得到真实的温度场，则需要在ANSYS中运用APDL语言在丝杠上施加往复移动的热源载荷。

在ANSYS中，对流系数与热流密度同时加载在同一位置时，只默认读取最后施加的边界条件，螺母在丝杠的有效工作行程内每移动1次，在前一位置处删除热流密度，施加对流载荷，再在新的位置处删除对流载荷，并施加热流密度，进行求解。如此往复进行，直到滚珠丝杠副中的丝杠、螺母和轴承温度不再升高，达到热平衡。

3 滚珠丝杠热特性分析

3.1 热平衡评定标准

在滚珠丝杠副中，单位时间内流入的热量和流出的热量相等，系统达到热平衡状态，其热态几何精度达到稳定值。如果滚珠丝杠副以某一恒定进给速度空载进给时，当温升达到最大温升的95%时，可以判定系统达到热平衡状态。在实际工况下，丝杠达到热平衡的时间与丝杠的传热系数、丝杠周围空气的流动速度，丝杠两端轴承的润滑冷却系数等因素有关。

3.2 丝杠转速对系统热平衡的影响

由图2和图3可知，在未通冷却液的情况下，当空载进给系统转速为800r／min时，滚珠丝杠热平衡时间为3 500s，热平衡温度为36.6℃，丝杠在前2 000s内温升比较大。前轴承热平衡时间为3 300 s，前1 500s，温度变化比较大，其平衡温度是31.3℃。后轴承热平衡时间是2 800s。后轴承的整体温升变化不明显，其平衡温度是21.2℃。

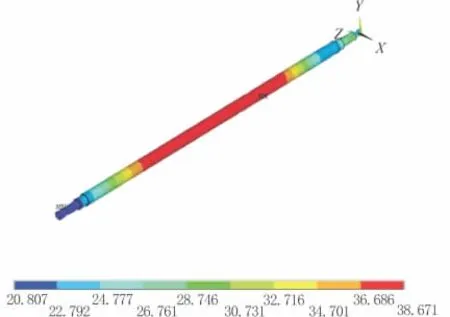
图2 滚珠丝杠进给系统温度分布

图3 进给系统的温升曲线

由图4和图5可知，当进给系统的转速为1 000 r／min时，滚珠丝杠热平衡时间为2 900s，在2 000 s前丝杠温升明显，其平衡温度为38.2℃。前后轴承的热平衡时间分别为2 600s和2 400s，其平衡温度分别为32.1℃和24.2℃，但是前轴承温升变化比较大。

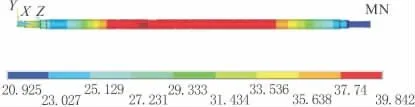
图4 滚珠丝杠进给系统温度分布

图5 进给系统的温升曲线

当丝杠转速分别为500r／min，800r／min和1 000r／min时，提取丝杠上某一点进行分析。通过图6可知，在进给系统中，滚珠丝杠的转速越高，摩擦产生的热量也就越多，达到热平衡的时间就会缩短。所以增大进给速度可以缩短热平衡时间，但达到热平衡的温度变高。

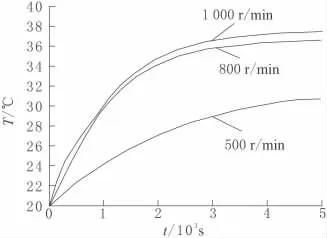
图6 不同进给速度丝杠一点温升曲线

3.3 冷却液对系统热平衡的影响

中空丝杠不仅具有质量小的特点，也可以降低丝杠在工作时的热效率，并且可以高精度运行。本次模拟主要讨论中空丝杠冷却液对丝杠温度场的影响。当丝杠空载转速为1 000r／min进给时，通入2L／min流量的冷却液，经过加载移动热源载荷，得到丝杠上一点的温升曲线，如图7所示。

由图7可以看出，冷却液对丝杠的温度变化有影响，在冷却液的作用下，丝杠的热平衡温度降低，而且缩短热平衡时间。当冷却液流量为2L／min时，达到稳态的时间大致为1 600s，此时的稳态温度为13.1℃。

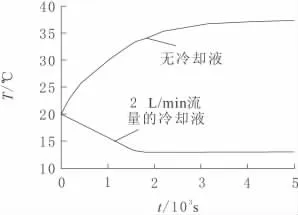
图7 不同冷却液下丝杠温升曲线

4 建立热误差模型

用灰色关联以及模糊聚类分析，选出对TX1600G数控镗铣加工中心工作方向X轴的热变形影响最大的测温点。根据经验，在进给系统中选取的测温点依次为：丝杠两端的轴承以及丝杆上一点。

机床进给系统的热变形是一个非线性的、随温度变化的时变过程。BP神经网络［10］具有并行性、冗余性以及本身的非线性自适应等特点，并且容错能力强，广泛使用在实际中。BP网络结构包括输入层、输出层以及隐含层，其中隐含层可分为单层和若干层。每层之间由权值对各个神经单元进行连接，而层内的神经元之间彼此独立。

由于进给系统热误差机理十分复杂，单一的模型难以全面考虑进给系统热误差的变化趋势和影响因素，所以单一模型在实际预测中的精度较低。灰色神经网络是将灰色系统和BP神经网络综合起来，使得预测精度提高，可以更好地预测热误差变形。具体的建模步骤为：

a.经过灰色关联分析模型，并经过筛选准则，建立温度变数列组成矩阵P，对矩阵P和滚珠丝杠X方向变形建立GM（1，K）模型；得到的实测值进行相减得残差e（0）（t）为：

b.把矩阵P前20组数据作为BP神经网的输入，同时把残差序列e（0）（t）作为输出，则BP神经网络模型具有了残差序列的多输入单输出的特点。用训练好的BP神经网络模型预测出的残差序列为＾e（0）（t｛｝），那么灰色神经网络组合模型的热误差结果为：

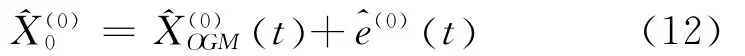
假设滚珠丝杠进给方向（X方向）的热误差X0，和经灰色关联分析筛选出来的温度变量X1，X2，…，Xk，组成原始数列。

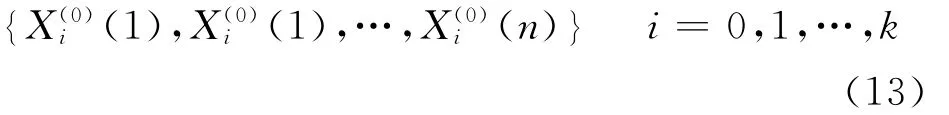
将上述数列分别作1次累加生成，得到新的数列：

灰色系统模型的还原值为：

5 结束语

TX1600G数控镗铣加工中心结合镗床和铣床的结构特征，具备立式铣床和卧式镗床的双重功能，可以实现X、Y、Z轴按一定规律联合运动。而滚珠丝杠热变形影响加工精度和定位精度。利用ANSYS分析滚珠丝杠转速为500r／min，800r／min，1 000r／min时，丝杠的温度场和冷却液对滚珠丝杠温度场的影响，得到以下结论：

a.在不同进给速度条件下，滚珠丝杠转速越高，摩擦产生的热量也越多，热平衡温度变高，但系统达到热平衡的时间缩短了。

b.分析冷却液对滚珠丝杠热平衡的影响，冷却液可以有效地缩短滚珠丝杠的热平衡时间，可以降低热平衡温度，减小滚珠丝杠的热变形。

［1］ Du D，Liu Y，Yan C，et al.An accurate adaptive parametric curve interpolator for NURBS curve interpola-tion［J］.International journal of advanced manufacturing technology，2007，32（9／10）：999-1008.

［2］ Ziegert J C，Kalle P.Error compensation in machine tools：a neuralnetwork approach［J］.Journal of Intelligent Manufacturing，1994，5（3）：143-151.

［3］ 易学平.丝杠结构热变形及近似估算探讨［J］.机械工程与自动化，2011，166（3）：170-171.

［4］ 何振.机床滚珠丝杠系统特性分析及其热变形补偿［D］.成都：西南交通大学，2005.

［5］ 夏军勇，吴波，胡友民.多变化热源下的滚珠丝杠热动态特性［J］.中国机械工程，2008，19（8）：955-958.

［6］ 黄俊，袁军，汪振华，等.基于有限元法的滚珠丝杠进给系统热特性分析［J］.组合机床与自动化加工技术，2014（3）：5-8.

［7］ 杨世铭，陶温铨.传热学［M］.北京：高等教育出版社，2006.

［8］ 张伟，叶文华.基于灰色关联和模糊聚类的机床温度测点优化［J］.中国机械工程，2014，25（2）：456-460.

［9］ 万长鑫，滚珠轴承的分析方法［M］.北京：机械工业出版社，1985.

［10］ 汪样兴，王树林，张云峰，等.数控机床热误差灰色神经网络补偿应用究［J］.机械设计与制造，2014（7）：236-239.