LCL型并网逆变器双闭环控制方法的研究

杜志华

（煤炭工业太原设计研究院，山西 太原 030001）

引言

随着世界经济的迅猛发展，世界各国对能源需求急剧增长，导致以煤、石油、天然气为主的传统能源面临枯竭，而以太阳能、风能、生物能为主的可再生能源清洁无污染，只要合理利用就能够满足全球50%的能源需求。并网逆变器是新能源并网的接口装置［1－2］，将可再生能源转换为电网能接纳的电能。理想的入网电流是完美的正弦波，较 低 的 总 谐 波 失 真 （total har monic distortion，T HD）是并网逆变器控制所追求的目标。

为了降低入网电流的T HD，逆变器拓扑需包含滤波环节。并网逆变器滤波器一般有L和LCL两种类型［3－6］。单L滤波器结构简单，控制容易，但高频谐波衰减能力不强；LCL滤波器对高频分量呈高阻抗，能够很大地衰减高频谐波电流，但该系统为三阶系统，存在谐振峰，对系统的控制策略提出更高的要求。采用单环入网电流直接来对并网逆变器进行控制，系统存在谐振尖峰，导致系统不稳定［7－8］。电容两端串联电阻的方法，可以有效抑制谐振尖峰，但降低了滤波器的高频滤波效果，增加了系统的损耗［9］。采用逆变侧电流反馈控制方法，可以增强系统稳定性，但不能实现对并网电流的直接控制［10］。

本文提出并网电流外环电容电流内环的双环控制策略，该方法内环采用电容电流反馈控制来抑制系统谐振峰，外环采用入网电流直接反馈控制，能够降低并网电流的谐波畸变率，提高并网逆变器输出电能质量。

1 并网逆变器拓扑

LCL型单相并网逆变器拓扑如图1所示。

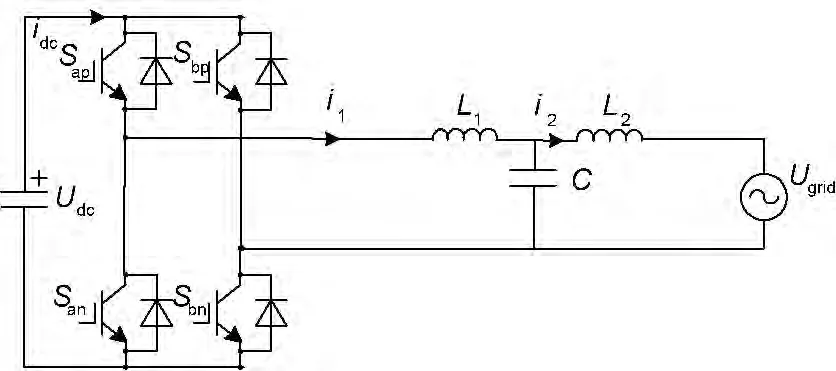
图1 LCL型并网逆变器电路拓扑

图1 中：Udc为直流侧电压；idc为直流侧输出电流；San、Sap、Sbn、Sbp为构成全桥逆变电路的四个开关管；L1、L2、C分别为LCL滤波器的滤波电感及滤波电容；i1为逆变器逆变侧的电流；i2为逆变器并网侧电流；Ugrid为单相电网电压。当开关频率远高于输出滤波器的截止频率时，逆变桥可等效为比例环节KPWM。

忽略滤波电感的电阻和电容的寄生电阻，由图1的拓扑可得出如图2 LCL滤波结构图。

图2 LCL滤波的结构图

通过LCL滤波结构图，可以得出其幅频特性如图3所示。从图中可以看出LCL型滤波器较L滤波具有更好的高频滤波性能，但LCL滤波器为三阶结构，在谐振频率处有较高的谐振尖峰，造成系统不稳定，所需要进行阻尼抑制。

图3 L型滤波与LCL型滤波的频率特性图

2 谐振阻尼抑制

图4为单环入网电流直接反馈控制闭环控制框图。由系统控制框图可推导出系统的开环传递函数为公式（1）。

图4 入网电流反馈控制框图

由公式（1）画出系统频率特性图，如图5所示。可以看出该系统在谐振频率处仍存在谐振尖峰，容易造成系统不稳定。由系统传递函数可看出，该系统有位于S平面右半部分的极点，可见对于LCL型并网逆变器系统，单环并网电流反馈控制闭环控制会导致系统不稳定。

电容电流反馈能实现谐振的抑制，电容电流反馈控制如图6所示。

图5 单环并网电流反馈控制系统开环频率特性

图6 电容电流反馈控制框图

电容电流反馈控制与单环并网电流反馈控制对比图，如图7所示。从图中可以看出，电容电流反馈控制能够很好地抑制谐振尖峰，并且在高频段并没有降低滤波器性能。

图7 电容电流反馈控制与单环并网电流反馈控制幅频特性图

3 双闭环控制策略的设计

由上述可知，电容电流反馈能够抑制谐振，增强系统稳定性。本文提出一种入网电流外环电容电流内环的双环控制策略，如图8所示，利用电容内环来抑制系统谐振，增强系统稳定性，外环在内环闭环的基础上能够直接对并网电流进行控制，提高系统的控制精度。

图8 双环控制系统框图

3.1 闭环系统设计

双环控制系统由外环和内环构成。首先需要设计内环参数，在内环设计的基本上进行外环的设计。

3.1.1 内环设计

由图8可得出电容电流内环的闭环传递函数为：

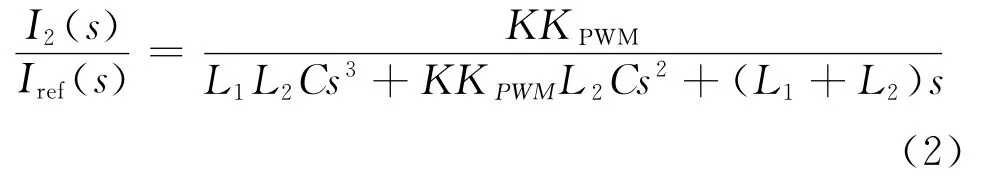
系统的阻尼比：

从公式（3）可看出系统阻尼比与内环控制参数成正比，系统阻尼比越大，对谐振尖峰的抑制能力越强，但过大的阻尼比将导致系统的动态响应能力较差。为同时兼得系统动态响应能力和谐振尖峰的抑制效果，一般工程经验值［12］ζ＝0.707。

3.1.2 外环设计

由于控制对象模型本身是由全控型开关器件以及二极管组成，系统为非线性系统，在建模时将其线性化，所以控制系统参数与真实值有一定的偏差。为解决上述问题，在设计系统调节器，必须留有足够的域量，一般工程经验为相角裕度MP＝30°～70°，幅值裕度MG＝6～8 d B。

图9双闭环控制系统的等效框图。公式（4）所为双闭环控制系统的开环传递函数，由传递函数可看出系统为Ⅱ阶系统，根据自动控制原理，针对二阶系统一般采用“振荡指标法”进行系统整定。增大积分系数能够提高系统跟踪给定的能力，但也会给系统带来不利影响，能够降低系统的相角裕度，同样，较大的比例系数能够增加系统带宽，增强系统的动态响应能力，但会减少系统幅值裕度，使系统不稳定。所以需要进行参数的合理设计，既保证系统具有稳态控制精度高，又要满足系统的动态响应速度快的能力。

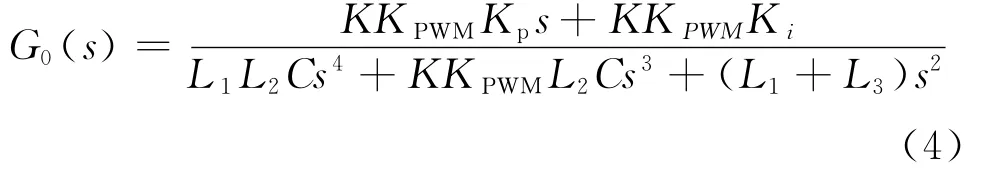
3.2 稳定性分析

由双闭环系统等效框图可得到系统闭环传递函数为：

图9 双闭环等效框图

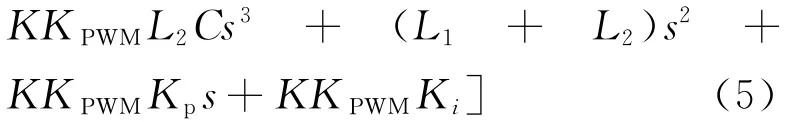
双闭环控制系统的特征方程为：

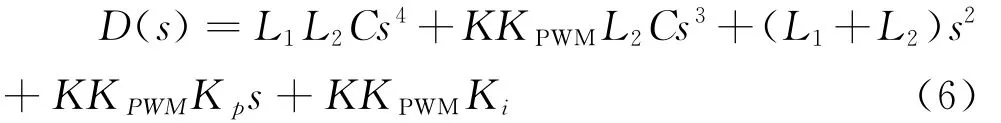
根据劳斯判据，系统稳定性条件为：

并网电流外环电容电流内环的双闭环系统的稳定条件如公式（7）。从公式（7）可看出，不等式中含有电容项，当积分系数较小时，KKPWMKiL2C忽略不计，比例系数Kp＜1＋L2／L1。当积分系数较大时，KKPWMKiL2C就不能忽略，但电容容值非常小，所以KKPWMKiL2C也非常小，Kp取值有所变化。

4 仿真和实验验证

经过上述双闭环系统的设计，在Simulink仿真环境中搭建了控制系统的仿真模型。图10、下页图11分别为并网电流电压稳态波形和并网电流的谐波失真率。从图中可看出入网电流能够完美地与电网电压保持同频同相，并且系统的稳态精度较高，谐波失真率仅为0.89%。

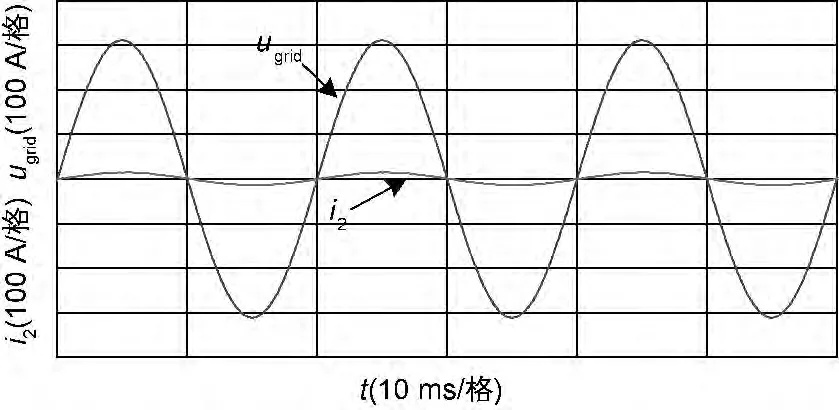
图10 并网电流电压仿真波形

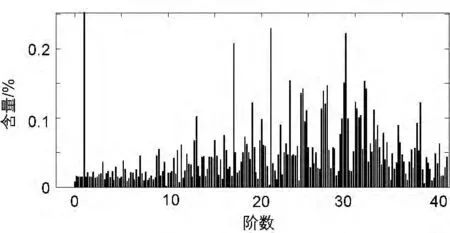
图11 并网电流仿真的THD

本文研制了一台2.2 k VA实验样机，在该样机上验证了该算法。图12、图13为并网的实验电流电压波形和电流的谐波失真率波形图。从图中可以看出LCL滤波器对并网电流起到了很好的高频衰减作用，抑制了开关频率处的谐波分量，而且电容电流反馈很好地抑制了谐振尖峰，降低了入网电流的谐波失真率，提高了系统的稳态精度。

图12 并网电流电压实验波形

图13 并网电流实验的谐波失真率

5 结语

LCL型并网逆变器存在固有的谐振尖峰，采用传统单环并网电流反馈控制，不能对谐振峰进行阻尼作用，因而系统不稳定。针对该情况，本文提出了一种电网电流外环电容电流内环的双闭环控制方法，详细推导了系统的传递函数，并对控制系统内外环进行详细设计，在Simulink仿真环境中搭建了仿真模型，最后在2.2 k VA并网逆变器试验台上进行实验，实验结果证明本文所提的双闭环控制方法能够大大抑制系统谐振尖峰，并提高了系统的稳态控制精度，改善了入网电能质量。

［1］ Bull S R.Renewable ener gy today and tomorrow［J］.Pr oceedings of the IEEE，2001，89（8）：1 216-1 226.

［2］ 由世俊，杨洪兴，娄承芝，等.建筑物用光伏集成系统在中国应用的前景［J］.太阳能学报，2000，21（4）：434-438.

［3］ 王飞，余世杰，苏建徽，等.光伏并网发电系统的研究及实现［J］.太阳能学报，2005，26（5）：605-608.

［4］ 赵清林，郭小强，邬伟扬.单相逆变器并网控制技术研究［J］.中国电机工程学报，2007，27（16）：60-64.

［5］ Serpa L A，Ponnaluri S.A.Modified direct power control strategy allowing the connection of three-phase inverters to the grid through LCL filters［J］.IEEE Transactions on Industry Applications，2007，43（5）：1 388-1 400.

［6］ Bueno E J，Espinosa F，Rodriguez F J，et al.Current control of voltage source converters connected to the grid through an LCL-filter［C］.IEEE PESC，Aachen，Ger many，2004.

［7］ ZuéA O，Chandra A.Simulation and stability analysis of a 100 k W grid connected LCL photovoltaic inverter for industry［C］.IEEE Power Engineering Society General Meeting，Montreal，Canada，2006.

［8］ Twining E，Holmes D G.Grid current regulation of a three-phase voltage source inverter with an LCL input filter［J］.IEEE Transactions on Po wer Electronics，2003，18（3）：888-895.

［9］ 张承慧，叶颖，陈阿莲，等.基于输出电流控制的光伏并网逆变电源［J］.电工技术学报，2007，22（8）：41-45.

［10］ 张强，张崇巍，张兴，等.风力发电用大功率并网逆变器研究［J］.中国电机工程学报，2007，27（16）：55-59.