基于浅层地震的三维训练图像获取及应用

张文彪，段太忠，郑 磊，刘志强，许华明，赵 磊

(中国石化 石油勘探开发研究院,北京 100083)

基于浅层地震的三维训练图像获取及应用

张文彪，段太忠，郑 磊，刘志强，许华明，赵 磊

(中国石化 石油勘探开发研究院,北京 100083)

多点地质统计学是当前研究的热点，其中训练图像的获取是关键环节，直接决定了储层模拟的精度和可靠程度。基于浅层高频地震信息，对浅层水道沉积的形态特征及定量规模展开研究，并通过相似性类比作为原型模型，指导深层油田区水道砂体形态规模统计，并在高精度反演数据基础上建立了具有代表性的定量化三维训练图像；以此为基础，借助petrel软件平台，通过设置训练图像不同网格大小，分析了其对多点地质统计模拟结果的影响。研究表明：该方法得到的训练图像真实可靠，模拟结果均忠实于井点数据，且砂体整体分布特征具有受训练图像约束的特点，当三维训练图像与实际模拟区网格大小一致时，模拟结果最能体现不同微相间的空间结构与几何特征。本文提供了一个训练图像获取的新思路，对具有相同地质条件的其他深水沉积微相类型的模拟具有借鉴作用。

三维训练图像；原型模型；多点地质统计学；深水水道;储层模拟

建立符合实际的地质模型一直是石油地质工作者们追求的目标，国内外学者多基于密井网资料、野外露头以及现代沉积获取先验认识，然后采用传统地质统计学方法开展沉积微相随机模拟研究，但都具有一定局限性[1-4]。多点地质统计学(MPS:Multiple-Point Statistics)在这种情况下应运而生，该方法综合了基于目标和两点地质统计学的优势，可以描述具有复杂空间结构的地质体，也是今后地质统计学发展的一个热门方向。

多点地质统计学应用难点在于训练图像的获取，以往训练图像制作多以密井网区资料为基础[5-9]，通过单井内插和外推进行模式拟合，获取不同微相的平面形态特征，得到二维训练图像。该方法制作的训练图像很大程度上依赖于地质人员推测，不确定性较大，且仅能反映平面二维空间的相带变化，对于三维的空间结构难以描述，尤其对于摆动频繁的水道(河道)沉积类型，常规二维训练图像显然更难以描述水道变化频繁的沉积过程，需要能够表征空间结构关系的三维训练图像。三维训练图像的获取是核心问题，高频地震资料是其重要来源之一，海上油田往往具有高品质地震资料，尤其是浅层沉积的地震主频能达到70 Hz，为训练图像的研究提供了较好的资料基础。

本文以西非海上B油田为例，首先论证了浅层沉积作为原型模型的可行性，通过剖析浅层水道沉积的高频地震信息，确立了单一水道的形态规模及迁移模式，建立了定量且符合沉积模式的三维训练图像；然后，基于该训练图像，采用多点地质统计学方法对实际油田区渐新统O73(渐新统第7油组下的第3砂组)砂组进行水道沉积模拟应用；最后，分析了建立训练图像时不同网格大小对实际模拟结果的影响。

1 研究区概况

研究区B油田位于西非下刚果盆地南端，现今大陆斜坡的中部位置，水深1 300～1 500 m。该油田2007年投产，目前有直井24口，平均井距1 000 m。主力含油层系为古近系渐新统O73砂组，为典型的深水水道沉积体系，主要发育水道和天然堤微相，相带分布稳定，无明显突变，适应于训练图像的平稳性。目的层系受深度及盐棚遮挡影响，地震成像模糊，分辨率较低(主频25 Hz)，难以清晰刻画单一水道砂体空间分布。

研究区浅层(上新统)同样沉积了一套水道砂体，沉积期构造稳定，形态保存完整，地震分辨率高(主频70 Hz)。浅层沉积是目前研究深水沉积原型模型的一个重要来源，在沉积背景相似度高的情况下具有很好的指导作用，同时较其它类型原型模型(露头、现代沉积、密井网)具有一定优势[10-14]：①资料精度有保障(海上高密度采集、高分辨率处理)；②工区范围足够大，容易把握并分析完整沉积形态；③可从平面、剖面及三维空间描述沉积形态特征；④能提供较充分的定量关系研究样品点。

该区充分依托浅层高频地震的优势，通过反射结构分析、地震反演以及多属性提取对水道特征开展定量研究。本文就浅层与深层水道沉积特点进行了相似性类比：地理位置相同，均位于西非安哥拉深水区，区域构造上，均位于挤压构造和拉张构造的转换带(过渡区)上，沉积物源同为北东方向刚果河水系，沉积背景为典型的深水浊流沉积环境，水体整体表现为水退背景；从盆地背景上看，均属于被动大陆边缘盆地(下刚果-刚果扇盆地)，沉积相类型都属于水道型海底扇浊流沉积，沉积地形均位于中陆坡位置(发育中-高弯度水道)。由此可见，浅层与深层待研究区沉积环境极为相似，可利用浅层水道作为原型模型指导B油田渐新统O73砂组储层研究。

2 多点地质统计学优势

传统基于象元的两点统计算法很难综合更多的形态信息，因此美国斯坦福大学研究者提出了多点地质统计随机模拟，目前代表性算法包括两种[15-16]：Snesim算法和Simpat算法，其中Snesim算法在目前商业软件(Petrel和RMS)中最为常用。多点统计应用“训练图像”取代变差函数来表达地质变量的空间结构性，综合了基于象元和目标的算法优势，一定程度上克服了传统地质统计学描述复杂空间结构和几何形态地质体的不足，而且模拟过程仍然以象元为模拟单元，采用序贯(非迭代)算法，容易忠实井点硬数据且模拟速度快。

多点地质统计学在建模中的优势主要体现在以下几个方面[1,17-18]：①在模拟具有复杂形状地质体分布时可以联合反映空间多个位置点的几何形状和配位关系；②考虑了储层在特定水动力条件下的沉积模式、沉积过程与沉积响应；③模拟过程综合了地质学家经验以及模拟对象的先验认识，较其他建模方法更真实反映地下储层分布；④多点地质统计学模拟算法快速灵活，易于多次模拟进行模型优选。

3 训练图像获取研究

建立训练图像是多点地质统计学的关键环节和基础。首先，基于研究区浅层地震资料分析，获取水道的形态特征、规模分布及定量关系；然后通过定量关系类比，指导B油田目的层单井钻遇水道砂体规模分析；最后在浅层高频地震反演资料中提取三维水道目标地质体，建立定量化三维训练图像。

3.1 深水水道沉积模式

单一水道是水道体系形成过程中的基本成因单元[19-20]，单一水道的侧向、垂向迁移形成了不同规模的复合水道分布。先验认识(三维训练图像)不仅要能反映出单一成因单元的定量几何形态，而且要有各成因单元的定量组合模式，并能体现出不同演化阶段的储层构型特点。因此，开展单一水道的形态及演化研究有助于更加深入了解复合水道的形成过程，指导实际生产，有效降低开发风险。然而，单一水道属小尺度单元，稀井网很难控制住水道砂体边界。为此，基于浅层高频地震反射结构分析，从剖面和平面上分析水道迁移模式。

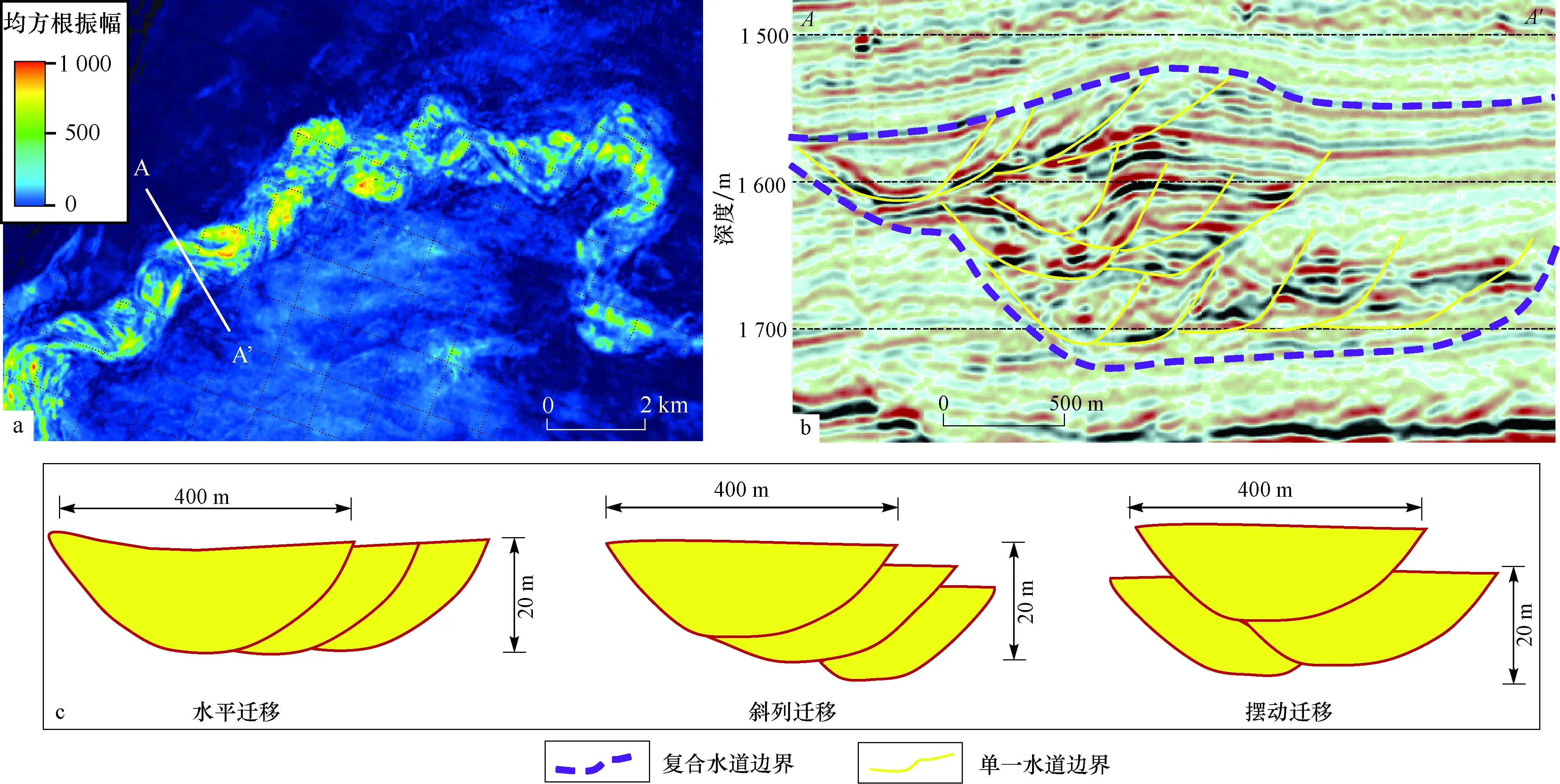
图1 浅层水道平面、剖面形态特征Fig.1 Shallow turbidity channel morphological characteristics on plane and sectional viewsa.浅层水道平面分布特征；b.水道剖面反射特征；c.单一水道摆动模式

单一水道为一次性成因单元，砂体厚度由水道中部到边部逐渐减薄，反映在振幅能量特征上则中部强、边部弱。图1a为浅层地震均方根振幅(RMS)地层切片，能清晰反映出水道的平面形态，且复合水道内部单一水道呈现出整体迁移特征[21-22]。从地震反射剖面来看受水道迁移特征及内部泥质含量变化的影响，单一水道边界处振幅发生明显变化，多数表现为振幅减弱，局部受切叠影响呈现出振幅增强特点，且地震剖面上呈现出一定的叠瓦状特征。从图1b和图1c可以看出单一水道剖面迁移模式可分为侧向、斜列和摆动三种类型，侧向迁移造成水道间侧向拼接，砂体垂向厚度与单一水道深度接近；而斜列和摆动迁移造成水道在垂向上叠置，砂体厚度多大于单一水道深度(厚度)。

3.2 深水水道形态规模

关于水道(河道)的定量规模关系，以陆相曲流河的研究最多也最为成熟，而且具有经验公式供借鉴[23]。对于深水水道的规模及定量关系研究仍然是当前的热点[24-26]。本文从最小沉积单元(单一水道)入手，提取了研究区浅层地震属性(RMS)大量地层切片，选择8条典型单一水道作为样本(图2a)，从深度域地震剖面上直接对其宽、深进行测量(图2b)，测量样品点52个，统计结果可作为该地区经验数据用于指导地下古水道储层构型规模认识。

对测量数据进行统计分析，结果表明：①单一水道的深度一般介于13～34 m，平均为22 m，深度为20～30 m的水道占60%(图3a)；②单一水道的宽度一般介于170～430 m，平均为290 m，宽度为200～350 m的水道占72%(图3b)；③单一水道的宽深比一般介于11～22，平均为14(图3c)。

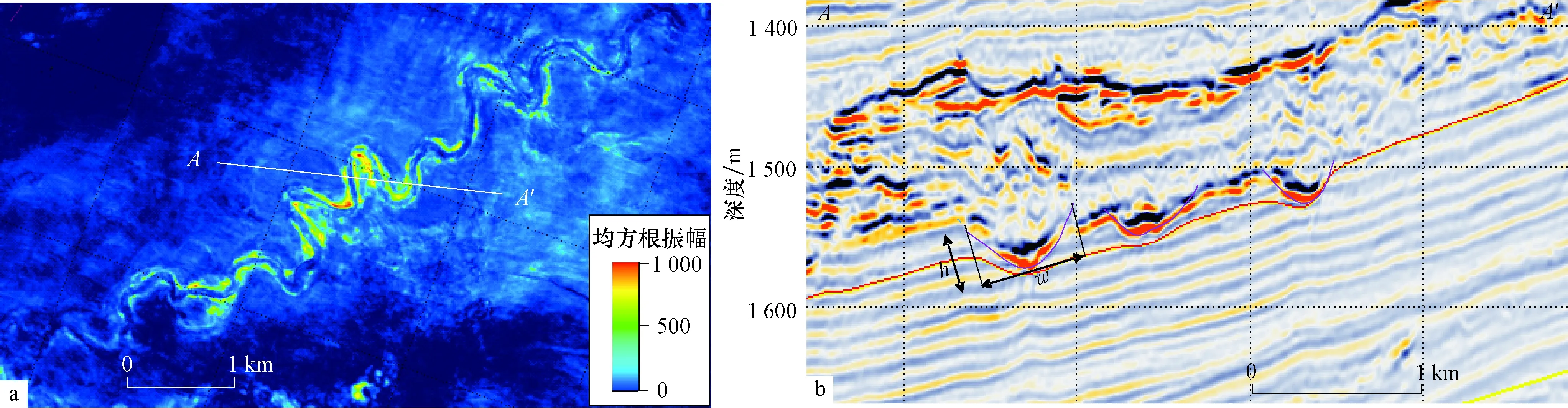
图2 浅层单一水道规模测量Fig.2 Measurement of single shallow turbidity channel scalea.浅层单一水道地震提取；b.单一水道宽度、深度测量

在对单一水道宽、深统计的基础上，进一步分析了两者相关性。分析认为，单一水道深度(h)与宽度(w)之间存在明显的线性正相关关系(图3d)，关系式为：h=0.069 7w+1.710 5，复相关系数(R2)为83%，即在单一水道形成过程中随着深度增加，其宽度也在增加。

3.3 应用区水道定量特征

研究区储层主要为水道沉积并伴有天然堤发育。受岩性分布规律影响，单井上测井曲线特征明显，水道呈钟形或箱型，天然堤以齿化箱型为主，均相对易识别(图4)。根据研究区开发井钻遇的水道砂体资料(厚度)，可以借助原型模型统计的经验公式确立实际模拟区单一水道发育规模。首先，对各单井微相类型进行解释，并统计单井解释的单一水道砂体厚度分布范围为8～23 m，平均为13 m；根据上述经验公式计算得到单一水道砂体宽度分布范围为91～305 m，平均为162 m；通过类比浅层水道的规模参数分布，认为计算结果可信。

3.4 训练图像产生

训练图像是能够表述储层结构、几何形态及其分布模式的数字化图像。它反映了地质学家对地下储层分布情况的定量化认识，训练图像相当于定量的相模式，是对实际储层先验认识的体现。本次基于浅层地震的波阻抗反演数据，通过地球物理雕刻技术提取浅层水道三维目标体(图5)，将该目标体在petrel软件中进行网格化，并依据目标体波阻抗绝对值分布范围将沉积微相划分为水道和天然堤两类，背景相为泥岩。图6为本次建立的反映水道、天然堤砂体与水道间泥岩分布的三维训练图像。从平面能体现出水道的展布形态，天然堤沿水道两侧边部分布；三维栅状图剖面上水道呈“顶平底凸”状，且单一水道间的迁移、叠置关系明显，符合地质模式，说明该训练图像比较可靠。三维训练图像从空间上提供了微相砂体间的几何关系，指示意义更接近地质实际。

4 训练图像应用研究

本次训练图像应用基于Petrel软件平台，采用目前多点地质统计学常用的Snesim算法，以井点测井相为硬数据，借助生成的三维训练图像对实际油田区水道砂体分布进行模拟。模拟过程主要包括建立训练图像网格、设置搜索面罩并扫描训练图像、构建稳定的搜索树、调整规模和方向匹配参数、序贯求取各模拟点数据事件的条件概率分布函数并抽样获得模拟实现，这一过程均通过Petrel软件完成。

图4 模拟区O73砂组单井微相解释及对比关系Fig.4 Single-well microfacies interpretation and correlation of O73 sand group in the simulation area

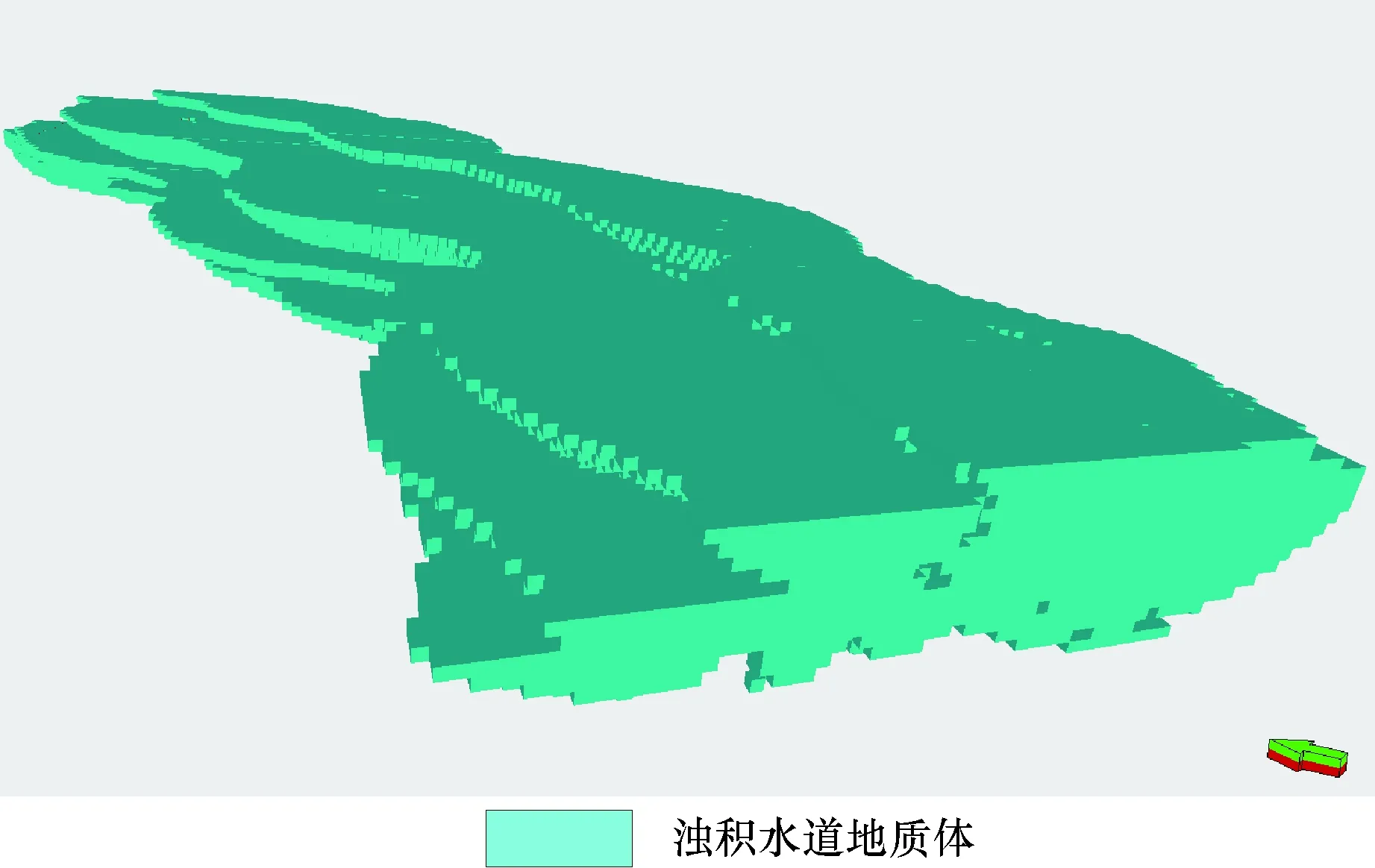
图5 浅层地震波阻抗反演资料中提取的水道地质体Fig.5 Channel geologic body extracted from shallow seismic impedance inversion

4.1 模拟关键步骤

训练图像网格设置的大小很重要，为探索不同网格大小对最终模拟结果的影响，本次尝试了3种不同尺寸的网格加以测试，分别为(1/2，1，2)倍于实际模拟区网格尺寸；训练图像网格的数量也有一定限制，I，J方向50～200个，K方向15～20个单元格即可满足要求，训练图像整体网格数量与实际模型网格数量的比控制在30%以内较合适；构建搜索树时的搜索面罩参考水道沉积的变差函数分布范围；为保证训练图像的平稳性，沉积微相类型和结构尽量保持简单，控制在2～5个相类型，本次模拟实例为水道和天然堤两种类型，相序相对简单，比较符合该方法的应用。

模拟过程中还有一些约束条件的限制，包括方向(rotation)的调整、规模(scaling)系数的设置。由于训练图像本身与模拟区的沉积物源相同，网格方向设置也相同，所以方向(角度)保持不变即可；规模系数的设置则需要参考前面研究成果，获取办法为用浅层水道宽度(或深度)平均值除以实际模拟区水道宽度(或深度)平均值，计算结果为1.79，即训练图像(浅层)砂体规模约为实际模拟区砂体规模的1.8倍；软数据约束则加入了地震波阻抗反演的成果。最后，根据O73砂组的小层划分结果(Ⅰ，Ⅱ)及井间对比关系(图4)分层展开模拟，并在模型比选的时候考虑小层内部及小层间水道砂体叠置关系是否合理。

4.2 模拟结果分析

依据上述步骤对实验区O73砂组沉积微相分布开展模拟研究。图7a为训练图像网格大小与模拟区网格大小一致(比例为1 ∶1)情况下的三维模拟结果，图中可见，沉积微相模拟结果忠实于井信息，且微相剖面(图7b)几何形态和展布满足训练图像的特征；图7c，7d和7e为模型中从上到下抽取的3个地层网格切片，体现出复合水道垂向上的演化特征和继承性，反映了训练图像的结构性。此外，当训练图像网格大小与实际模拟区网格大小不一致(本次选取比例1/2和2)情况下，通过保持其他模拟条件不变，也得到了相应的模拟结果。

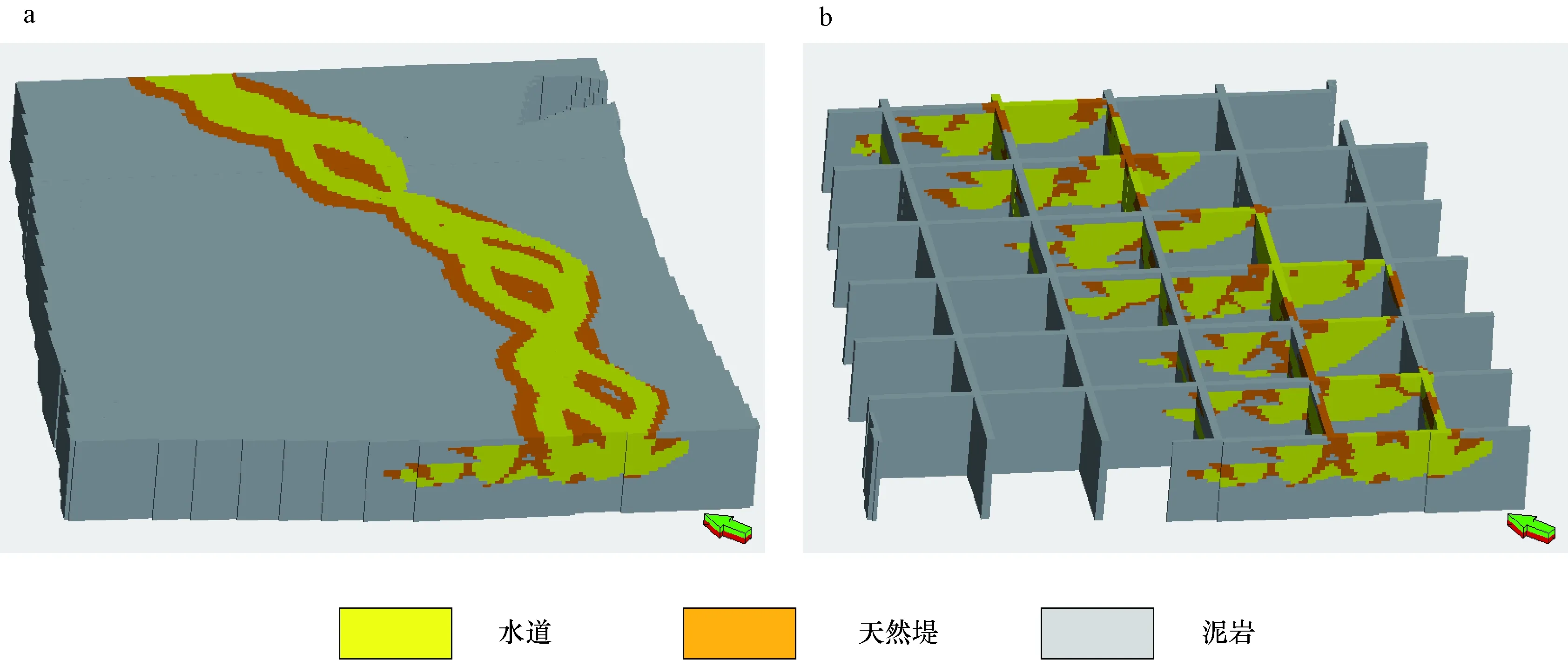
图6 基于浅层水道目标体得到的三维训练图像及栅状图显示Fig.6 Three-dimensional training images and fence diagram generated based on shallow turbidity channela.水道三维训练图像；b.三维训练图像栅状图显示

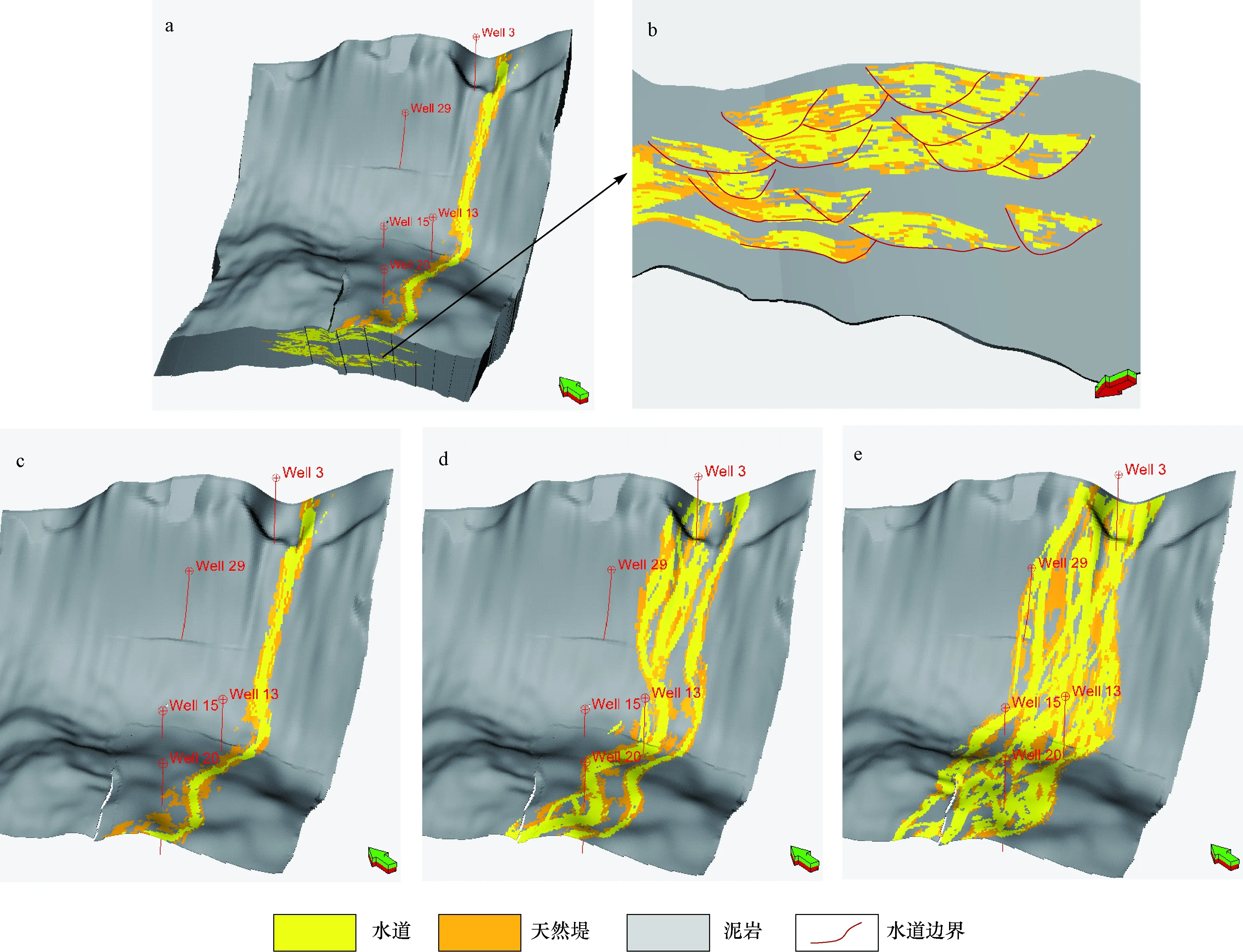
图7 多点地质统计学方法模拟水道三维分布结果Fig.7 3-D channel distribution from simulation based on multi-point geological statisticsa.三维模拟实现；b.模拟结果剖面显示；c.地层网格切片1；d.地层网格切片9；e.地层网格切片17

针对前面提出的关键步骤，对三种网格尺寸情况下的模拟结果进行了比较分析(图8)，当训练图像网格尺寸小于(图8a)或者大于(图8c)实际模拟区网格情况下，模拟结果无论从连续性还是相分布结构来看都要差于网格尺寸相等情况下(图8b)的结果。分析原因可能是搜索树的稳定程度以及抽样条件概率分布函数的精度都与网格的匹配程度有关。当网格不匹配的情况下，训练图像的模式信息多少会存在损失，且搜索树扫描的过程中会出现偏离现象。当然不可能保证每个训练图像都能与模拟区位于同一时空域，以确立相同的网格。当时空域不匹配的情况下，还是需要明确一个合适的范围，既保证训练图像模式信息不损失，还能与实际模拟区有较好的匹配，这些还需要后续更多的试验研究来讨论。当然，由于算法(Snesim)本身存在局限性(不连续性)，导致局部水道(天然堤)出现不连续现象，这可以在后续工作中人工适当处理。总之，该方法在水道模拟中具有较好的适用性。

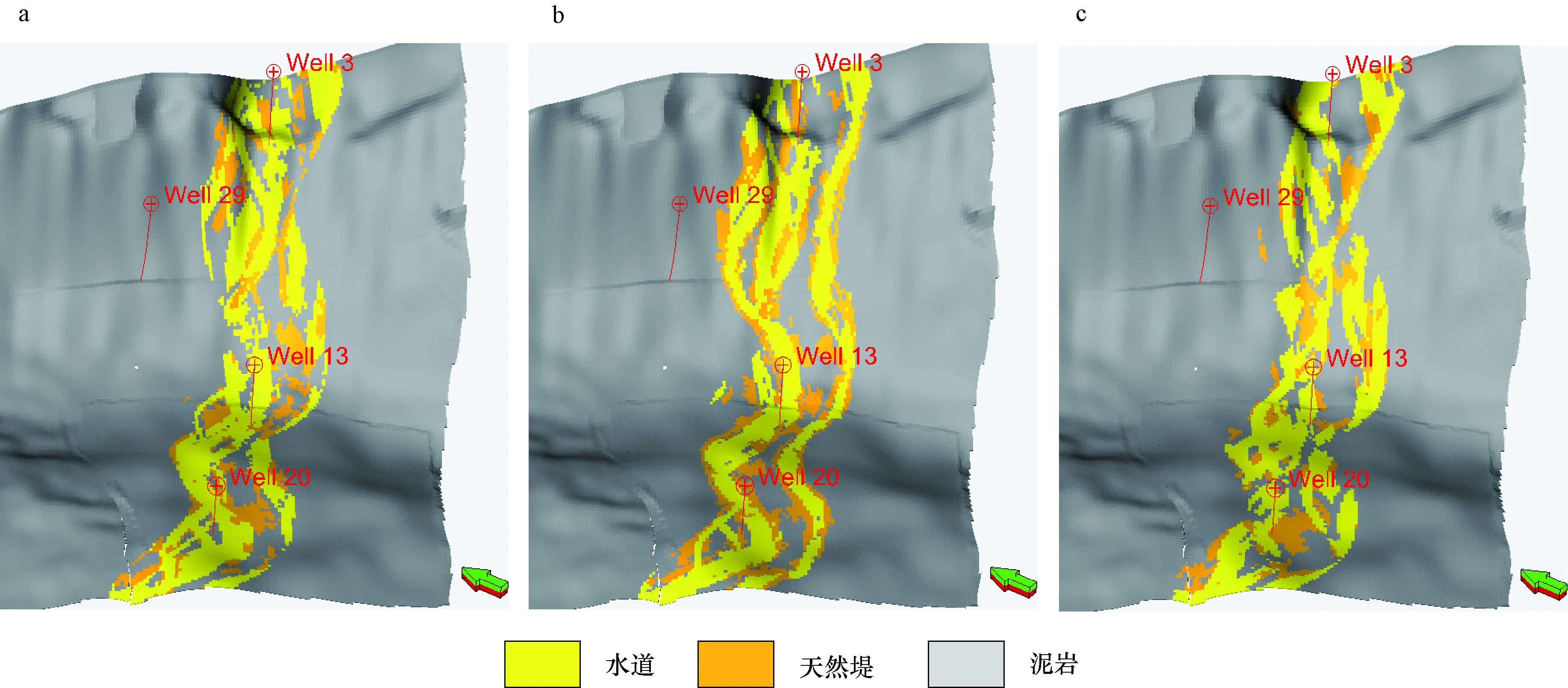
图8 训练图像与模拟区不同网格尺寸比例条件下模拟结果对比Fig.8 Comparison of simulation results obtained at different grid sizes of training images and simulation areaa.比例为1 ∶2；b.比例为1 ∶1；c.比例为2 ∶1

5 结论

1) 浅层沉积是原型模型的重要来源之一，较其它类型原型模型(露头、密井网区等)具有空间分布的优势，沉积背景相似是类比的重要基础，定量形态规模和统计参数是类比的主要对象。

2) 借助浅层高频地震可以建立三维训练图像，基于该图像的储层模拟结果空间结构清晰，分布合理；本次应用发现当训练图像网格大小与实际模拟区网格大小一致时，模拟结果最符合先验认识。

3) 将浅、深层地质资料结合，运用类比方式建立定量化三维训练图像并用于实际油田区模拟，该方法提供了一种获取三维训练图像的思路，对其他深水沉积类型(扇体、朵叶)的模拟研究具有借鉴意义。

4) 训练图像与实际模型网格不匹配情况下，会导致训练图像的信息损失和搜索树扫描过程的偏离，影响模拟结果；为便于工作中实际操作，仍需要明确一个合适的匹配范围，这些还需要后续更多的试验研究来讨论。

[1] 于兴河.油气储层表征与随机建模的发展历程及展望[J].地学前缘，2008(01)：1-15. YuXinghe.A review of development course and prospect of petroleum reservoir characterization and stochastic modeling.EarthScience Frontiers,2008,15(1):001-015

[2] 吴胜和，李文克.多点地质统计学：理论、应用与展望[J].古地理学报，2005，7(1):137-143. Wu Shenghe，Li Wenke.Multiple-point geostatistics:theory，application and perspective[J].Journal of Palaeogeography，2005，7(1):137-143.

[3] 段冬平，侯加根，刘钰铭，等.多点地质统计学方法在三角洲前缘微相模拟中的应用[J].中国石油大学学报(自然科学版)，2012，36(2):22-26. Duan Dongping，Hou Jiagen，Liu Yuming，et al.Application of multi-point geostatistics in delta front microfacies simulation[J].Journal of China University of Petroleum (Edition of Natural Science)，2012，36(2):22-26.

[4] 尹艳树,吴胜和.储层随机建模研究进展[J].天然气地球科学,2006,17(2):210-216. Yin Yanshu,Wu Shenghe.The process of reservoir stochastic modeling[J].Natural Gas Geoscience，2006，17(2):210-216.

[5] 张丽，孙建孟，孙志强，等.多点地质统计学在三维岩心孔隙分布建模中的应用[J].中国石油大学学报(自然科学版)，2012，36(2):105-109. Zhang Li，Sun Jianmeng，Sun Zhiqiang，et al. Application of multiple-point geostatistics in 3D pore structure model reconstruction[J].Journal of China University of Petroleum (Edition of Natural Science)，2012，36(2):105-109.

[6] Strebell E S，Journel A G．Reservoir modeling using multiple-point statistics[R].SPE 71324，2001.

[7] Strebell E S.Conditional simulation of complex geological structures using multiple-point statistics[J].Mathematical Geology，2002，34(1):1-21.

[8] Strebell E S，Journel A G.Rerervior modeling using multiple-point statistics[R].SPE 71324，2001:1-11.

[9] 周金应，桂碧雯，林闻．多点地质统计学在滨海相储层建模中的应用[J].西南石油大学学报:自然科学版，2010，32(6):70-74. Zhou Jinying，Gui Biwen，Lin Wen.Application of multiple-point geostatistics in offshore reservoir modeling[J].Journal of Southwest Petroleum University(Science & Technology Edition)，2010，32(6):70-74.

[10] 李少华，张昌民，林克湘，等.储层建模中几种原型模型的建立[J].沉积与特提斯地质，2004，24(9):102-106. Li Shaohua，Zhang Changmin，Lin Kexiang，et al.The construction of prototype models in reservoir modeling[J].Sedimentary Geology and Tethyan Geology，2004，24(9):102-106.

[11] 崔廷主，马学萍.三维构造建模在复杂断块油藏中的应用-以东濮凹陷马寨油田卫95 断块油藏为例[J].石油与天然气地质，2010，31(2):198-205. CuiTingzhu，Ma Xueping.Anapplication of 3D structural modeling to complex fault-block reservoir：A case of the lower unit reservoir of Sha-3 member in Block Wei-95[J].Oil & Gas Geology，2010，31(2):198-205.

[12] 胡光辉,王立歆,王杰,等.基于早至波的特征波波形反演建模方法[J].石油物探,2015,54(1):71-76 Hu Guanghui,Wang Lixin,Wang Jie,et al.Characteristics waveform inversion based on arly arrival wave[J].Geophysical Prospecting for Petroleum,2015,54(1):71-76

[13] 鲁新便，赵敏，胡向阳，等.碳酸盐岩缝洞型油藏三维建模方法技术研究——以塔河奥陶系缝洞型油藏为例[J].石油实验地质,2012,34(2):193-198. Lu Xinbian,Zhao Min,Hu Xiangyang,et al.Studies of 3D reservoir modeling:taking Ordovician carbonate fractured-vuggy reservoirs in Tahe Oil Field as an example[J].Petroleum Geology & Experiment,2012,34(2):193-198.

[14] 唐洪，廖明光，胡俊，等.基于孔隙旋回建模单元的碳酸盐岩储层建模研究[J].石油实验地质,2012,34(3): 330-333. Tang Hong,Liao Mingguang,Hu Jun,et al.Research on carbonate reservoir matrix model building based on porosity cycles[J].Petroleum Geology & Experiment,2012,34(3): 330-333.

[15] 张伟，林承焰，董春梅.多点地质统计学在秘鲁D油田地质建模中的应用[J].中国石油大学学报:自然科学版，2008，32(4)，24-28. Zhang Wei，Lin Chengyan，Dong Chunmei.Application of multiple-point geostatistics in geological modeling of D Oilfield in Peru[J].Journal of China University of Petroleum(Edition of Natural Science)，2008，32(4):24-28.

[16] Zhang Tuanfeng.Incorporating geological conceptual models and interpretations into reservoir modeling using multiple-point geostatistics[J].Earth Science Frontiers，2008，15(1):26-35.

[17] Arpat B G，Cacrs J.A multi-scale，pattern-based approach to sequential simulation[J].Geostatistics Banff.2004，1(10):255-264.

[18] 尹艳树，吴胜和，张昌民，等．基于储层骨架的多点地质统计学方法[J].中国科学D辑:地球科学，2008，38(增刊Ⅱ):157-164. Yin Yanshu，Wu Shenghe，Zhang Changmin，et al.Based on reservoir skeleton multi-point geostatistics[J].Scientia Sinica Terrae(Ser D)，2008，38(supⅡ):157-164.

[19] 万琼华，吴胜和，陈亮，等.基于深水浊积水道构型的流动单元分布规律[J].石油与天然气地质，2015(02)：306-313. Wan Qionghua，Wu Shenghe，Chen Liang，et al.Analysis of flow unit distribution based on architecture of deep-water turbidite channel systems[J].Oil & Gas Geology，2015(02)：306-313.

[20] Russell B，Wynn Al E.Sinuous deep-water channels: Genesis，geometry and architecture[J].Marine and Petroleum Geology.2007，24:341-387.

[21] 鲁新便,何成江,邓光校,等.塔河油田奥陶系油藏喀斯特古河道发育特征描述[J].石油实验地质,2014,36(3):268-274. Lu Xinbian,He Chengjiang,Deng Guangxiao,et al.Development features of karst ancient river system in Ordovician reservoirs,Tahe Oil Field[J].Petroleum Geology & Experiment,2014,36(3):268-274.

[22] 林煜，吴胜和，王星，等.尼日尔三角洲盆地深水油田A海底扇储层质量差异[J].石油与天然气地质，2014(04)：494-502. Lin Yu，Wu Shenghe，Wang Xing，et al.Reservoir quality differences of submarine fans in deep-water oilfield A in Niger Delta Basin，West Africa[J].Oil & Gas Geology，2014(04)：494-502.

[23] 李宇鹏，吴胜和，岳大力.现代曲流河道宽度与点坝长度的定量关系[J].大庆石油地质与开发,2008,27(6):19-22. Li Yupeng，Wu Shenghe，Yue Dali.Quantitative relation of the channel width and point-bar length of modern meander river[J].Daqing Petroleum Geology and Oil Development，2008，27(6):19-22.

[24] 王香文，刘红，滕彬彬，等.地质统计学反演技术在薄储层预测中的应用[J].石油与天然气地质，2012，33(5)：730-735. Wang Xiangwen,Liu Hong,Teng Binbin，et al.Application of geostatistical inversion to thin reservoir prediction[J].Oil & Gas Geology,2012，33(5)：730-735.

[25] 钱玉贵，叶泰然，张世华，等.叠前地质统计学反演技术在复杂储层量化预测中的应用[J].石油与天然气地质,2013,34(6)：834-840. Qian Yugui，Ye Tairan，Zhang Shihua,et al.Application of pre-stack geo-statistics inversion technology in quantitative prediction of complex reservoirs[J].Oil & Gas Geology,2013，34(6)：834-840.

[26] Wood L J，Mize-Spansky K L.Quantitative seismic geomorphology of a Quaternary leveed-channel system，offshore eastern Trinidad and Tobago，northeastern South America[J].AAPG Bulletin，2009，93(1):101-125.

(编辑 张玉银)

Generation and application of three-dimensional MPS training images based on shallow seismic data

Zhang Wenbiao,Duan Taizhong,Zheng Lei,Liu Zhiqiang,Xu Huaming,Zhao Lei

(PetroleumExploration&ProductionResearchInstitute,SINOPEC,Beijing100083,China)

Multi-point geological statistics is one of the hot spots in current study,and the creation of training image is a key part determining the accuracy and reliability of reservoir simulation.Based on the shallow high frequency seismic data,the morphology and quantitative aspects of shallow channel deposits are studied and used as prototype models for further investigation of morphology and scale statistics of channel sand body-ies in deeper oil reservoiors.Quantitative three-dimensional training image is established on the basis of high-precision seismic inversion data.Training image grids are selected and Petrel is applied to analyze its impact on multi-point geological statistics.Results show that simulation is consistent with the well point data,and the spatial morphology and sizes of different channels are constrained by the quantitative characteristics of training image.Simulation results can best reveal the geometric characteristics and spatial confi-guration of sedimentary facies when the grid size of 3-D training image is consistent with the actual grid of simulation model.It provides a new method to create the training image,and may serve as a reference example for the simulation of other types of deep-water sedimentary facies.

three-dimensional training image，prototype model，multi-point geological statistics，deep-water channel，reservoir simulation

2015-01-19;

2015-07-16。

张文彪，男，(1984—)，硕士、工程师，精细油藏描述及开发地质。E-mail:zwb.syky@sinopec.com。

中国石化科技部攻关项目(G5800-15-ZS-KJB016)。

0253-9985(2015)06-1030-08

10.11743/ogg20150619

P631

A