计算风工程中的网格技术对比研究

康忠良 方媛媛

(1.中国建筑科学研究院建研科技股份有限公司，北京 100013；2.北京市燃气集团研究院，北京 100011)

计算风工程中的网格技术对比研究

康忠良1方媛媛2

(1.中国建筑科学研究院建研科技股份有限公司，北京 100013；2.北京市燃气集团研究院，北京 100011)

通过对比风工程数值模拟中可供选择的各种网格技术，深入分析了几种网格各自的特点。结构网格与非结构网格的优缺点基本是对立互补的，混合网格技术代表了当前和未来网格技术的主要发展趋势。自适应笛卡尔网格自动化程度高，对于各向同性流动问题极具优势。由于目前从事计算风工程的专业人员网格生成能力较差，自适应笛卡尔网格特别适合于风工程的低速复杂湍流问题的模拟。

计算风工程；网格技术；自适应笛卡尔网格

1 引言

计算流体力学(CFD)是一门利用计算机技术和数值方法对流体力学问题进行模拟与分析的新型交叉学科，它的出现为流体力学的应用与发展提供了一种新的手段。几十年来，CFD得到了长足的发展，在航空航天、建筑、机械、气象和生物医学等领域得到了广泛应用。它的发展主要是围绕着数值方法和网格技术这两条主线不断进步的。

基于CFD的计算风工程技术，是近二十年来国内外建筑领域风工程研究的热点问题。由于风工程中建筑环境及模型的复杂性、流动的低速域和流场的大分离涡结构等特点，从事数值模拟的数值方法和网格技术应进行合理选用。目前，已有文献对适用于计算风工程的网格技术的深入比较和分析尚少，因此，本文就适用于风工程的网格技术展开讨论。

2 网格技术的发展

人们最初是基于单区结构网格进行数值计算。随着几何模型的日趋复杂，为降低结构网格生成难度，多区对接[1]、多区拼接网格[2]和结构重叠网格技术[3]等网格类型陆续被提出，并得到了广泛应用。然而对于复杂构型，结构网格的生成依然是一项十分艰巨的经验性任务。因此，CFD的一个发展重点后来也集中到了非结构网格技术及其计算方法的研究上，这主要是由于非结构网格对复杂构型的强大拓扑能力以及对流动特征的自适应能力。对于非结构网格的应用，最初主要采用各向同性的四面体单元，这对于求解Euler方程是足够的，但对于NS方程的粘性计算还需要在边界层附近构造各向异性网格[4]，于是混合网格技术应运而生。

混合网格可以根据具体的复杂外形和流场特征充分发挥不同网格单元类型各自的优势，代表了当前和未来网格技术的主要发展趋势[5]。

近年来，实际应用中存在的一些复杂工程问题也对网格技术提出了新的要求，比如在模拟多体间具有相对运动的复杂非定常流动问题时，就必须采用相应的动网格技术。由于必须在每个时间步更新网格，因此动网格技术成为这类非定常流动模拟的关键技术之一。目前常用的动网格技术主要包括：超限插值动网格技术[6]、自适应笛卡尔网格技术[7]、结构网格重叠技术[8]、非结构网格重叠技术[9]、非结构重构动网格技术[10]、非结构变形动网格技术[11]以及变形/重构动态混合网格技术[12]等。

3 网格技术对比

由于计算风工程问题具有空间拓扑复杂、无相对运动和无网格变形等特点，因此可供选择的网格技术主要有结构网格、非结构网格、混合网格和自适应笛卡尔网格，下面对这几类网格进行详细对比分析。

3.1 结构网格

结构网格存储简单、索引便捷、可以达到计算资源的高效利用。基于结构网格的CFD计算方法比较成熟，对于目前广泛采用的基于一维流动理论的CFD计算格式，结构网格良好的贴体特性能够准确地满足边界条件，最大限度地降低由于网格因素引起的计算耗散，从而提高计算精度和效率。另外，由于结构网格独特的几何特征，使得其可以方便地进行单方向加密，因此可以大大减少计算网格总量，降低计算代价，这一点在高雷诺数流动的粘性模拟中尤为重要。

3.2 非结构网格

非结构网格的最大优点是其几乎无所不能的几何适应能力，也就是对复杂构型强大的灵活性，其网格生成简单，尤其是网格生成的人工工作量少。非结构网格节点和单元的分布可控性好，能较好地处理边界，容易控制网格的大小和节点的密度，容易根据流动梯度和物体运动实现自适应。容易生成整体网格、整体求解，不像结构网格那样需要在分区边界传递信息，损失计算精度。非结构网格在并行计算中容易实现计算节点的负载平衡，非常适合于大规模分布式并行计算。

非结构网格也有很多缺点。它的CFD计算方法不成熟，很多已有的结构网格的数值算法不能直接用于非结构网格计算，尤其是对高阶格式的构造存在较大困难。隐式时间格式求解时，非结构网格的无序性也造成了稀疏矩阵和本身的非线性等问题。非结构网格的随机方向性造成了不易正确捕捉流场结构，导致了计算精度(尤其是粘性计算精度)降低及计算稳定性下降。非结构网格填充效率不高，尤其在粘性区里，非结构网格很难使用类似于结构网格的大长细比网格，必须在各个方向都布置很密的网格。非结构网格存储结构复杂，计算效率低，对计算机内存等硬件资源要求高。

3.3 混合网格

通过以上分析，可见结构网格与非结构网格的优缺点基本是对立的、互补的，为了充分吸收它们各自的优势，研究人员后来引入了混合网格形式。

CFD计算所采用的二维混合网格可以是多种形式，如图1所示。

CFD计算所采用的三维混合网格形式也可以是多种多样的，比如有四面体/三棱柱混合网格、四面体/三棱柱/金字塔/六面体混合网格等等，如图2所示。

对于异类理据构成的常用词而言,被用作借体的词,不仅要打破自身原有的指称对象范围所特有的格局,还要突破甚至进入与其有一定关联性的其他事物对象所在的特定范围,所以，必须要对原有的个别语义特征进行一定的调整和变化,使之能够把原有的语义特征和新调整的语义特征结合起来产生新的认知关联,并随之建立起一种新型的语义联系,实现对新的本体的代替和指称,产生其借代意义。

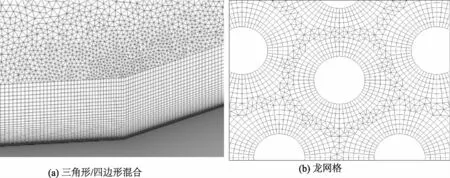
图1 二维混合网格示例

图2 混合网格实例

三维混合网格在壁面附近粘性作用区采用三棱柱和六面体单元，在外围流场区域采用四面体单元，中间采用金字塔过度。这种方法充分利用了三棱柱和六面体网格单元的高拉伸特性，一方面可以达到类似结构网格的粘性模拟能力，提高了计算精度；另一方面也有效降低了网格量，提高了计算效率。当然，混合网格单元类型也可以采用其它任意多面体，比如边界层附近是蜂窝状，空间是足球状等等。虽然这些方案各自取得了一定成功，但至今都没能彻底解决混合网格粘性计算的问题。

近年来，尽管混合网格生成方法一直在不断地发展和进步，但针对复杂外型的完全自动化网格生成和自适应调整技术依旧未能实现。一方面，无法生成高质量的网格成为目前混合网格技术发展的重要障碍，这也给重叠网格和笛卡尔网格技术留下了发展空间。另一方面，自适应网格的加密方法没有得到广泛应用，主要原因有以下两点：第一，该方法的操作在大型计算机上难以实现动态负荷的平衡；第二，缺乏可靠的误差评估技术来推动加密准则的发展。因此，目前混合网格的生成和自适应技术仍需要进一步的发展，才能得到更好地推广与应用。

3.4 自适应笛卡尔网格技术

自适应笛卡尔网格是一种从远场到边界的网格生成方法，它可以根据物面的几何特征，自动化对网格进行不断切分，最终形成逐渐加密的贴体网格，如图3所示。

自适应笛卡尔网格具有众多的优点：它不需要预先生成严格规定的某种物面网格，生成过程统一，不需要人为干预，相比于结构网格和非结构网格，它是真正的自动化网格；在方程求解过程中，由于网格边界与坐标轴平行，对于通量的计算量大大减少；特别对于各向同性流动问题极具优势。因此，自适应笛卡尔网格在近年来受到越来越多的青睐。

图3 自适应笛卡尔网格示例

但是，它也存在一些缺陷：如何生成变长宽比的网格单元，以适应几何外形和计算流场的需要，也是一个困难；切割所产生的极小网格，会影响到流场求解的稳定性和收敛性。

4 结论

(1)计算风工程可供选择的网格技术主要有结构网格、非结构网格、自适应笛卡尔网格和混合网格。

(2)结构网格计算优势突出，但几何构型的适应能力差，适用于简单模型建立。

(3)非结构网格几何构型的适应能力强，但计算方法与过程劣于结构网格，适用于复杂模型建立。

(4)混合网格技术代表了当前和未来网格技术的主要发展趋势。但针对复杂外型的完全自动化网格生成和自适应调整技术尚需要进一步的研究和发展。

(5)自适应笛卡尔网格自动化程度高，适用于复杂模型自动建立，不需人工干预，对于各向同性流动问题具有突出优势。由于建筑风工程问题一般是低速复杂湍流流动，因此适合于笛卡尔网格的各向同性特点，且目前建筑领域从事风工程数值模拟人员的CFD知识相对薄弱，网格生成能力相对较差，因此特别适合采用自适应笛卡尔网格。

[1] Sheng C, Taylor L, Whitfield D. Multiblockmultigrid solution of three dimensional incompressible turbulent flows about appended submarine configuration[R].AIAA-1995-0203.

[2] Flores J, Reznick S G, Holst T L. Transonic Navier-Stokes solution for a fighter-like configuration[R]. AIAA-1987-0032.

[3] Peace D G, Atanley S, Martin F. Development of a large Chimera grid system for space shuttle[R].AIAA-1993-0533.

[4] Frink N T, Shahyar Z Pirzadeh. Tetrahedral finite-volume solutions to the Navier-Stokes equations on complex configurations[R].NASA/TM-1998-208961.

[5] Baker T J. Mesh generation: art or science[J]. Prog.Aero. Sci., 2005, 41: 29-63.

[6]Nakamichi J. Calculations of unsteady Navier-Stokes equations around an oscillating 3D wing using moving grid system[R]. AIAA-1987-1158.

[7]AftosmisM J, BergerM J, Melton JE. Robustand efficientcartesian mesh generation for component-based geometry[R]. AIAA-1997-0196.

[8] Lijewski L E. Comparison of transonic store separation trajectory predictions using the Pegasus/DXEAGLE and DEGGER Codes[R]. AIAA-1997-2202.

[9] FumiyaTogashi, Yasushi Ito,Kazuhiro Nakahashi. Extensions of overset unstructured grids to multiple bodies in contact[J]. Journal of Aircraft, 2006, 43(1): 52-57.

[10]Griibe B, Carstens V. Computational of unsteady transonic flow in harmonically oscillating turbine cascades taking into account viscous effects[J]. ASME journal. Turbomachinery, 1998, 120(1): 104-111.

[11] Hassan O, Probert E J, Morgan K. Unstructured mesh procedures for the simulation of three-dimensional transient compressible inviscid flows with moving boundary components[J]. Int. J. Numer. Mesh. Fluids, 1998, 27: 41-55.

[12]张来平, 王振亚, 杨永健. 复杂外形的动态混合网格生成方法[J]. 空气动力学学报，2004, 22(2): 231-236.

Comparative Analysis on Grids Generation in Computational Wind Engineering

Kang Zhongliang1,Fang Yuanyuan2

(1.CABRTechnologyCo.,Ltd.，ChinaAcademyofBuildingResearch,Beijing100013,China；2.AcademyofBeijingGasGroupCo.,Ltd.,Beijing100011,China)

Several grid generation technologies are compared based on computational wind engineering. The advantages and disadvantages of structured grids and unstructured grids are opposite and mutually complementary, so mixed grids represent the current and future major development trend of grid generation. Adaptive Cartesian grids can be generated automatically, and show a great advantage for isotropic flow simulation. Adaptive Cartesian grids are particularly suitable for low speed complex turbulence flow simulation on wind engineering, for most professionals currently have a poor capacity for grid generation.

Computational Wind Engineering； Grids Generation Technology； Adaptive Cartesian Grids

“十二五”国家科技支撑计划(2012BAJ09B04)

康忠良(1981-)，工学博士。主要从事CFD技术和BIM技术研究。

TU13;TU17

A

1674-7461(2015)02-0080-04