黄土高原半干旱区油松人工林冠层截留降雨模拟与分析
尹准生, 孙长忠, 赵明扬, 王磊
(中国林业科学研究院华北林业实验中心,102300,北京)
黄土高原半干旱区油松人工林冠层截留降雨模拟与分析
尹准生, 孙长忠†, 赵明扬, 王磊
(中国林业科学研究院华北林业实验中心,102300,北京)
基于黄土高原半干旱区2012—2013年观测数据,采用定位研究方法对该区油松人工林林冠层降水再分配情况进行研究;采用王彦辉模型和崔启武模型对林冠截留量进行模拟并对其适用性进行对比分析。结果表明:1)油松人工林穿透雨量与林外降雨量呈显著线性关系(R2=0.978 9),林冠截留量与林外降雨量呈幂指数关系(R2=0.867 3),平均林冠截留率为25.5%;2)王彦辉模型和崔启武等模型模拟的决定系数R2分别为0.724 5和0.755 4,黄土高原半干旱区油松人工林林冠截留模拟效果崔启武模型较王彦辉模型要好。
油松; 林冠截留模型; 模拟; 林冠截留; 黄土高原
森林水文效应是森林生态系统重要的生态功能[1]。冠层截留作为森林降雨再分配的一部分,在森林水分循环过程中占据重要地位,直接影响着林分涵蓄降水能力的大小、产生地表径流的能力和林地土壤有效水分的多少[2-4]。影响林冠截留量的因素很多,包括林外降雨量、降雨强度、植被类型和冠层结构等[5-6]。林冠截留模型对于揭示林冠的截留作用和估算林冠截留量具有重要作用[7];因此,根据野外试验样地的实测资料,建立、检验和优化林冠截留模型,并通过模型研究林冠层截留特性仍是森林水文学的研究热点[8]。
到目前为止,国内外学者对林冠截留模型研究做了大量的工作,林冠截留模型主要分为理论模型、经验模型和半经验半理论模型[9]。理论模型经过严格的推理而来,刘家冈[10]通过描述林冠对降雨的截留过程推导出林冠截留降雨的理论模型,该模型机制性强,且模型中所有参数可测,能够准确地反映林冠截留各要素的动态过程;但由于理论模型结构复杂,参数的测定较为困难,所以,导致模型在实际应用上受到限制。经验模型是通过实测数据构建的水文模型,该类模型形式较多,结构简单,使用方便,通常只有林外大气降雨量一个因素,所以不能反映林冠层截留与各生态因子之间的关系。目前,国内外对于林冠截留的研究采用的较多的模型多为半经验半理论模型,其中以J.H.C.Gash[11]模型、崔启武等[12]模型和王彦辉[13]模型居多;但J.H.C. Gash模型需要详细的气象资料来确定其参数,所以导致模型参数精度很难保证,从而使模拟结果出现偏差较大[14]。而王彦辉模型和崔启武等模型相对其他模型而言,参数较少,模型结构简单,使用次降雨量即可运行,且国内目前应用较多,但针对这2个模型适应性对比的报道相对较少。因此,笔者通过分析黄土高原半干旱区油松人工林降雨再分配特征,选取王彦辉模型和崔启武等模型对该地区油松林林冠截留量进行模拟对比,选择最适合该地区的林冠截留模型及其参数,估算林冠截留量,旨在为黄土高原油松人工林林冠层水文效应的深入研究提供理论参考。
1 研究区概况
试验地位于山西省忻州市偏关县陈家营,E111°01′~111°22′,N39°12′~39°40′,海拔1 377 m,大陆性气候,年平均气温3.7 ℃,年平均降水量425.3 mm,全年60%以上的降水都集中在7—9月份,主要植被为乔木林和灌丛,造林树种主要为油松(PinustabulaeformisCarr.)、侧柏(Platycladusorientalis(L.)Franco)和樟子松(PinussylvestrisL.var.mongolicaLitv.)等。研究区为典型的黄土高原半干旱区,所观测油松纯林林龄为30年(经抚育的人工同龄林,林相整齐,单株差异较小)。
2 研究方法
2.1 样地设置
设置20 m×20 m油松标准地3个,平均树高4.8 m,平均胸径10.6 cm,郁闭度0.8。
2.2 气象因子测量
在林外附近空地设置小型气象站一个进行各气象因子的测定,在林内实验样地进行林内穿透雨和树干径流的观测。具体测量方法如下。
1)林外降雨的测定:林外小型气象站内安置一个雨量筒,测量每次降雨量即为林外降雨量。
2)林内穿透雨的测定:在每个林内实验样地具有代表性的区域选择一矩形(圆形)区块,取其对角线的两端及中点(圆心及任一直径的两端)进行雨量筒布设,布设3个,每次降雨后观测所得穿透雨量取其平均值即为林内穿透雨量。
3)树干径流的测定:每个样地选择标准木3株,将直径为10 cm的聚乙烯塑料管在树干胸径处缠绕2周,固定后将接缝处用密封胶封严,将软管下部伸入塑料桶,收集导入塑料桶内的降水,并使用量筒测量,通过公式计算即可求得树干径流量。计算公式为
(1)
式中:SF为树干径流量,mm;n为标准木株数;N为样地内的林木总株数;S为样地面积,m2;Ci为第i株标准木的树干径流体积,mL。
4)林冠截留量的测定:林冠截留量可以通过林冠层水量平衡原理计算得到,即林外降雨量减去林内穿透雨量和树干径流量计算得到。其相应的计算公式为
Ic=P-(TF+SF)。
(2)
式中:Ic为林冠截留量,mm;P为林外降雨量,mm;TF为林内穿透雨量,mm。
2.3 模型选取
选取王彦辉模型和崔启武等模型对黄土高原半干旱区油松人工林进行模拟分析。王彦辉模型和崔启武等模型均为半经验半理论模型,且只有次降雨量1个因素,在林冠截留模拟的研究中应用较广,故都可作为通用模型运用于本研究中。
1)王彦辉模型。是对Horton模型的简化,该模型将林冠截留降雨量分解为吸附截留量和附加截留量。模型方程为
(3)
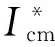
2)崔启武等模型。通过选取降雨量、相邻2次降雨的间隔时间和林冠特性作为影响冠层截留的主要因子建立的林冠截留模型。模型方程为
(4)
式中:A为实测林分郁闭度,%;r为通过实际情况确定的经验常数;I0为饱和截留量,mm,可根据实测资料或者经验确定;P′为达到饱和截留量时对应的林外降雨量,mm。
3 结果与分析
3.1 降雨再分配特征
试验期间(2012年4月—2013年9月)共观测降雨事件75场,累计总降雨量为1 106.4 mm,单次降雨量最大值为107.6 mm,单次降雨最小值为1.3 mm,单次平均降雨量为14.8 mm。
将2012—2013年林冠层降雨再分配数据汇总,结果见表1。
根据国家气象局规定的降雨级的分布,24 h次降雨量小于10 mm的为小雨,10~25 mm的为中雨,25~50 mm为大雨,50~100 mm为暴雨。由表1可知,试验观测期间小雨事件所占的频率为52%,中雨和大雨分别所占的频率为33.3%和10.7%,暴雨及以上降雨事件较少,频率仅为4.0%。观测期间累计穿透雨量为857.7 mm,穿透雨率为77.5%,采用75场次降雨数据,由对穿透雨量及林外降雨量进行回归分析(图1)可知,穿透雨量随林外降雨量的增大而增大,二者之间的关系可用线性函数表示(R2=0.978 9),由穿透雨率与林外降雨量关系图(图2)可知,穿透雨率随着林外降雨量的增大呈增大的趋势,二者之间呈幂指数函数相关关系(R2=0.471 9),当林外降雨量小于19.0 mm时,冠层对穿透雨的影响较大,但当林外降雨量大于19.0 mm时,随着林外降雨量的增大,穿透雨率逐渐趋于稳定。树干径流所占比例小,试验区内当降雨量大于6.0 mm时才有树干径流发生,树干径流量所占林冠降雨再分配的比例较小,平均树干径流率仅为1.5%。

表1 油松林冠层降雨再分配特征
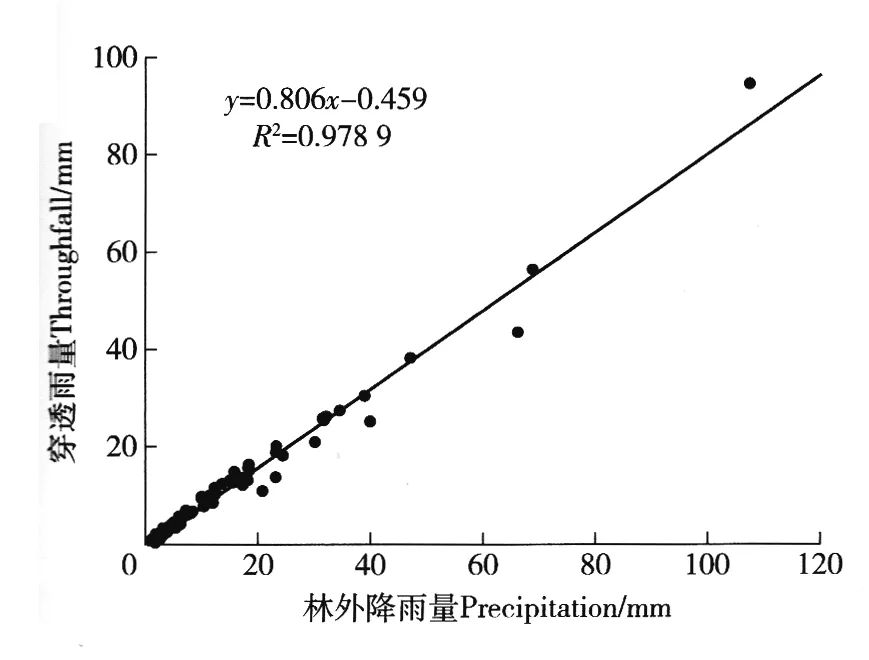
图1 林外降雨量与穿透雨量的关系Fig.1 Relationship between precipitation and throughfall
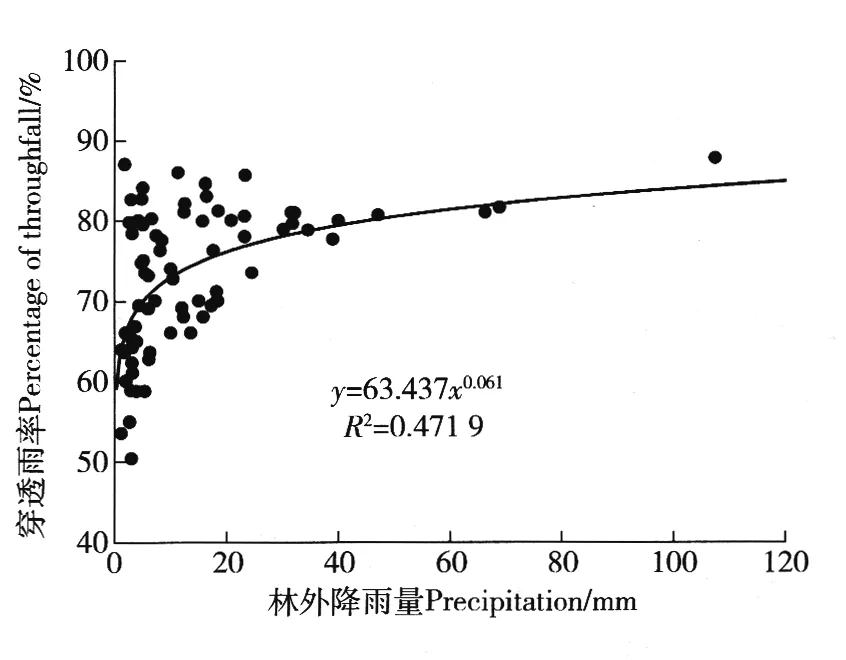
图2 林外降雨量与穿透雨率的关系Fig.2 Relationship between precipitation and percentage of throughfall
试验期间油松林累计林冠截留量为217.0 mm,占林外降雨量的19.6%,平均截留率为25.5%。由林冠截留与林外降雨量关系散点图(图3)可以看出,林冠截留量随林外降雨量的增大而增大,当林外降雨量增加达到一定值后林冠截留量增加幅度不明显,二者之间的关系可采用幂指数函数拟合(R2=0.867 3)。由林冠截留率与林外降雨散点图(图4)可以看出,随着林外降雨的增大,林冠截留率逐渐降低,二者之间呈负幂指数关系(R2=0.588 2),当林外降雨量级小于10 mm时,林冠层能够吸附的雨水所占林外降雨的比例较大,平均林冠截留率为29.9%。当林外降雨量级在10~25 mm时,林冠截留率变化在11.6%~33.0%之间,平均值为22.6%。随着林外降雨的增大,林冠截留逐渐趋于饱和,当降雨量大于25 mm时,林冠截留率变化幅度不大。
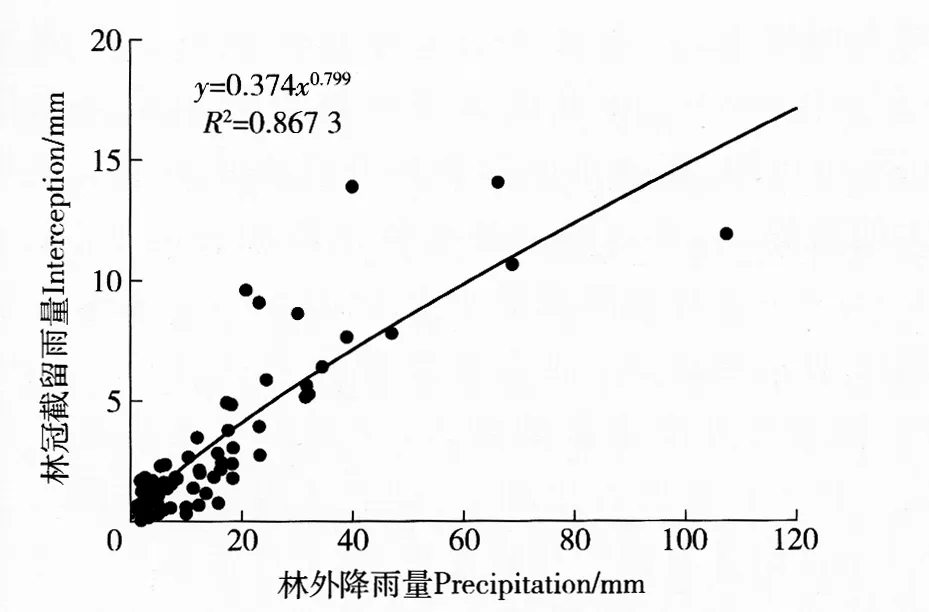
图3 林外降雨量与林冠截留雨量的关系Fig.3 Relationship between precipitation and interception
3.2 林冠截留模拟

选择崔启武等模型进行模拟之前必须确定经验常数r和饱和截留量I0。根据本试验中林冠截留量与林外降雨之间的关系,林冠截留量达到6.0 mm左右则趋于稳定,因此,选择I0=6.0 mm;经验常数r的确定一般与林冠截留率有关,根据相关文献[16-18]总结的二者之间的关系,同时结合本研究的平均林冠截留率25.5%,最后确定模拟模型的r值为0.8。通过计算,得出林冠截留达到饱和时的林外降雨量P′为 16.9 mm。
利用以上确定参数后的2个模型,并结合黄土高原半干旱区油松人工林2012年4月—2013年9月的75场降雨资料,对林冠截留进行模拟,2个模型的模拟结果分别见图5和图6。
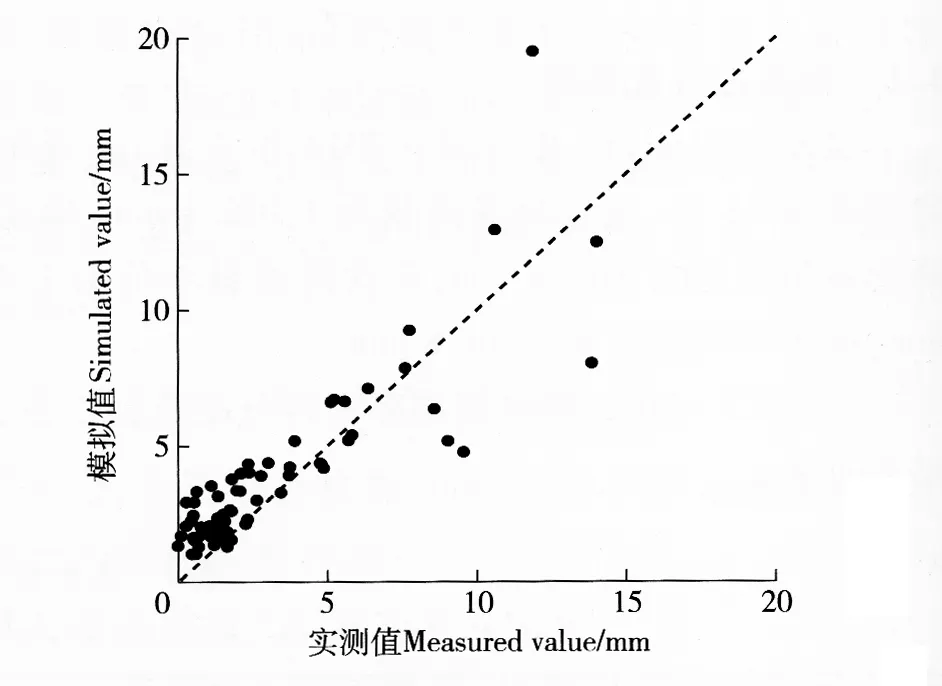
图5 王彦辉模型模拟油松林冠层截留量结果Fig.5 Simulation results of canopy rainfall interception for Pinus tabulaeformis stands using Wang’s model
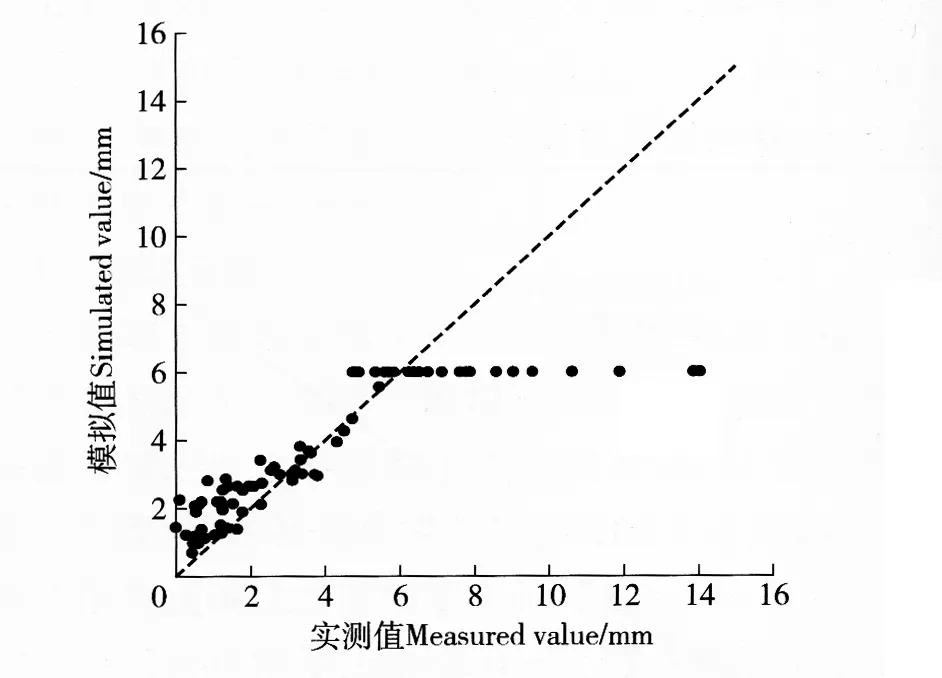
图6 崔启武等模型模拟油松林冠层截留量结果Fig.6 Simulation results of canopy rainfall interception for Pinus tabulaeformis stands using Cui’s model
由图5王彦辉模型拟合结果可知,当截留量小于4.0 mm时,模拟值大多都大于真实值,截留量大于4.0 mm时模拟效果相对较好,模拟值与实测值基本分布在1∶1线附近。
从图6也可以看出,当林冠层达到饱和之前,崔启武等模型具有较高的精度:当林冠截留量小于6.0 mm时,模拟值与实测值基本分布在1∶1线附近;当林冠截留大于6.0 mm时,由于林冠截留被视为一常数,但由于仍有蒸发存在,林冠截留量实际上仍处于增加状态,所以,此时崔启武等模型的模拟值均小于实测值。
对于所观测到的降雨,降雨量与时间呈现一定的正相关趋势,这样就会使林冠截留在达到饱和之后,仍有降雨在发生,且降雨量越大,时间也越长,饱和之后的总蒸发量也就越大。这就造成随着截留量的增加,偏差值也呈增大的趋势,这与图6显示的结果非常一致。从总的模拟结果来看:王彦辉模型和崔启武等模型对林冠截留模拟的总误差分别是-17.8和11.34 mm,决定系数R2分别为0.724 5和0.755 4;王彦辉模型模拟值的相对误差值范围为-7.6~5.9 mm,崔启武等模型模拟值的相对误差值范围为-2.13~8.05。2个模型模拟的平均绝对误差分别为1.24和1.12 mm,但对于林冠截留量8.0 mm以上的降雨,2个模型模拟效果均一般。
王彦辉模型将林冠截留中的附加截留项简化为林冠截留蒸发率和林外降雨量的乘积,并把林冠截留蒸发率假定为一个常数,这导致截留量小时模拟值大于实测值。崔启武等模型则忽略了降雨期间的林冠截留蒸发,认为林冠截留达到饱和后截留量数值不再变化,导致模拟达到饱和截留降雨后模拟值较实测值偏小。总体而言,王彦辉模型和崔启武等模型对于黄土高原半干旱区油松人工林的模拟还是成功的,模拟精度较高。
4 讨论
对2012年4月—2013年9月黄土高原半干旱区油松林冠截留进行分析得出,平均林冠截留率为25.5%,符合国内外学者的研究结果(平均林冠截留率变动范围为10%~45%[19]),略高于中国各森林生态系统林冠的平均截留率[20]。影响林冠截留的因素较多,主要有降雨量、降雨强度、空气温度、空气湿度、风速和植被特征等[21]。王彦辉模型将林冠截留降雨量分解为吸附截留量和附加截留量2部分,其中的附加截留量Ia项假定为降雨历时和林冠投影面积内的平均蒸发强度的乘积。考虑到模型不宜太复杂又将附加截留项简化为林冠截留蒸发率α和林外降雨量P的乘积(即Ia=αP),并且将蒸发率α假定为一个常数;而实际降雨过程中蒸发率α随着降雨量的增加而减小,所以必然导致模拟精度受到影响。崔启武等模型考虑了降水量,植被林冠特征以及林冠干湿程度等因子,但却忽略了林冠附加截留损失这一部分。周国逸[22]认为,当降雨量较大,并使林冠截留达到饱和时,林冠层的截留潜力由于水分蒸发的作用得以恢复,林冠层仍然可以继续截留少量降雨,相应的林冠层实际截留量将大于饱和截留量;因此,由于考虑一些实际情况,使得王彦辉模型和崔启武等模型在模拟林冠截留量时均存在不足之处。
本研究试验期间,2012和2013年均为丰水年,且2012年大雨以上次数较多,而恰巧2个模型对于降雨量较大时模拟截留量均存在缺陷,故较大降雨时导致模拟值与实测值差别较大,模拟截留总量相应也会产生误差。这也是本研究中2个模型模拟误差相对偏大的原因之一。对黄土高原半干旱区油松人工林,采用王彦辉模型和崔启武等模型进行对比发现,二者的决定系数R2分别为0.724 5和0.755 4,且误差值崔启武等模型较王彦辉模型稍好。由此可知,在该试验区域,考虑了降雨量和林冠特征2个因子的崔启武等模型要略好于只考虑降雨量1个因子的王彦辉模型。崔启武等模型的决定系数为0.755 4,说明降雨量和林冠特征只能解释该区域油松林冠截留量的75.54%的信息,剩余的24.46%的信息需要由降雨强度,降雨期间的空气温度、空气湿度、风速和气压等因素来解释。由于该模型的主要缺陷为林冠截留量达到饱和后忽略了林冠附加截留损失这一项,与现实情况不符;故日后的研究中可以着重对该模型这块进行优化,以建立更适用、模拟更精确的林冠截留模型,为林冠层水文效应的深入研究提供理论参考。
5 结论
1)黄土高原半干旱区油松人工林穿透雨量与林外降雨量呈显著线性关系(R2=0.978 9),林冠截留量与林外降雨量之间呈幂指数关系(R2=0.867 3),平均林冠截留率为25.5%,林冠截留率随着林外降雨的增大逐渐减少,随着林外降雨量增加到一定值后林冠截留率值变化不大。
2)采用王彦辉模型和崔启武等模型对油松林林冠层截留降雨量进行模拟,决定系数R2分别为0.724 5和0.755 4,模拟效果相对较好;对比2个模型模拟结果可知,黄土高原半干旱区油松人工林林冠截留模拟效果崔启武等模型较王彦辉模型要好。
[1] 刘世荣.中国森林生态系统水文生态功能规律[M].北京:中国林业出版社,1996:3-6
[2] 赵明扬,孙长忠,康磊.降雨再分配的回归模型差异性分析[J].中南林业科技大学学报,2013,33(5):79-84
[3] 王冉,王玉杰,王云琦,等.三峡库区典型常绿阔叶林冠层降雨截留模拟研究[J].长江流域资源与环境,2014,23(2):281-286
[4] Oishi A C, Oren R, Novick K A, et al. Interannual invariability of forest evapotranspiration and its consequence to water flow downstream[J].Ecosystems,2010,13(3):421-436
[5] Dietz J, Holscher D, Leuschner C, et al. Rainfall partitioning in relation to forest structure in differently managed montane forest stands in Central Sulawesi, Indonesia[J].Forest Ecology and Management,2006,237(1):170-178
[6] Muzylo A, Llorens P, Valente F, et al. A review of rainfall interception modelling[J].Journal of Hydrology, 2009,370(1):191-206
[7] 彭焕华,赵传燕,沈卫华,等.祁连山北坡青海云杉林冠对降雨截留空间模拟[J].干旱区地理,2010,33(4):600-606
[8] Komatsu H ,Shinohara Y, Kume T, et a1. Relationship between annual rainfall and interception ratio for forests across Japan[J].Forest Ecology and Management,2008,256(5):1189-1197
[9] Liu Shuguang. A new model for the prediction of rain fall interception in forest canopies[J].Ecological Modelling,1997,99(9):151-159
[10] 刘家冈.林冠对降雨的截留过程[J].北京林业大学学报,1987,9(2):140-144
[11] Gash J H C. An analytical model of rainfall interception by forests[J]. Quarterly Journal of Royal Meteorological Society,1979,105:43-55
[12] 崔启武,边履刚,史继德,等.林冠对降雨的截留作用[J].林业科学,1980,16(2):141-146
[13] 王彦辉.刺槐对降雨的截持作用[J].生态学报,1987,7(1):43-49
[14] 何常清,薛建辉,吴永波,等.应用修正的Gash解析模型对岷江上游亚高山川滇高山栎林林冠截留的模拟[J].生态学报,2010,30(5):1125-1132
[15] 王彦辉,于澎涛,徐德应,等.林冠截留降雨模型转化和参数规律的初步研究[J].北京林业大学学报,1998,20(6):25-30
[16] 卫三平,王力,吴发启.黄土丘陵沟壑区刺槐林冠截留模拟[J].林业科学,2008,44(1):26-33
[17] 佘冬立,刘营营,邵明安,等.黄土坡面不同植被冠层降雨截留模型模拟效果及适用性评价[J].农业工程学报,2012,28(16):115-120
[18] 王佑民.中国林冠降雨再分配研究综述[J].西北林学院学报,2000,15(3):1-7
[19] 曾伟,熊彩云,肖复明,等.不同密度退耕雷竹春季林冠截留特性[J].生态学杂志,2014,33(5):1178-1182
[20] 温远光,刘世荣.我国主要森林生态系统类型降水截留规律的数量分析[J].林业科学,1995,31(4): 289-297
[21] 鲜靖苹,张家洋,胡海波.森林冠层水文研究进展[J].西北林学院学报,2014,29(3):96-104
[22] 周国逸.生态系统水热原理及其应用[M].北京:气象出版社,1997:72-73
(责任编辑:宋如华)
Simulation and analysis of canopy interception onPinustabulaeformisplantations in semi-arid areas of the Loess Plateau
Yin Zhunsheng, Sun Changzhong, Zhao Mingyang, Wang Lei
(Forestry Experiment Center of North China, Chinese Academy of Forestry, 102300, Beijing, China)
We investigated the rainfall redistribution of canopy onPinustabulaeformisplantations in the semi-arid areas of the Loess Plateau based on the data collected from 2012 to 2013 using the permanent plot method. The canopy interception was simulated separately by using Wang′s and Cui′s interception models, and the applicability of the two models were compared. The results showed that: 1) There was a linear relationship between rainfall and throughfall (R2=0.978 9), but an exponential relationship between rainfall and canopy interception (R2=0.867 3), and the average of interception rate was 25.5%. 2) The determination coefficient of Wang’s interception model was 0.724 5 and it was 0.755 4 for Cui′s. In general, Cui′s interception model was slightly better than Wang′s.
Pinustabulaeformis; canopy interception model; simulation; canopy interception; Loess Plateau
2014-09-16
2015-04-06
项目名称: 国家自然科学基金“黄土高原半干旱区人工植被水分生态环境效应规律研究”(30170769)
尹准生(1988—),男,硕士研究生。主要研究方向:森林水文。E-mail:yinzhunsheng@163.com
†通信作者简介: 孙长忠(1957—),男,研究员。主要研究方向:森林培育与森林生态。E-mail: sun61@163.com
S715
A
1672-3007(2015)03-0045-06

