广义Rosenau-Kawahra方程的一个线性守恒差分格式
陈 涛, 胡劲松(西华大学 理学院, 四川 成都 610039 )
广义Rosenau-Kawahra方程的一个线性守恒差分格式
陈 涛, 胡劲松*
(西华大学 理学院, 四川 成都 610039 )
对一类广义Rosenau-Kawahara方程的初边值问题进行数值研究,提出一个三层线性差分格式,格式合理地模拟问题的一个守恒性质,得到了差分解的先验估计,利用离散泛函分析方法分析差分格式的二阶收敛性与无条件稳定性,并利用数值算例进行验证.
广义Rosenau-Kawahara方程; 有限差分格式; 守恒; 收敛性; 稳定性
为描述紧离散系统和模拟无线电及计算机领域中通过一个L-C流程的长链传输线模型,Rosenau方程[1-2]
ut+uxxxxt+ux+uux=0,
(1)
一经提出,就引起了众多学者的关注[3-7].但作为对非线性波的进一步考虑,需要对Rosenau方程(1)添加粘性项+uxxx和-uxxxxx,得到了Rosenau-Kawahara方程
ut+uxxxxt+ux+uxxx-uxxxxx+uux=0,
(2)
文献[8]讨论了方程(2)的孤波解和周期解,文献[9-10]又进一步给出了一类广义Rosenau-Kawahara方程的孤波解和2个守恒量.目前为止,仅有文献[11]对Rosenau-Kawahara方程(2)的定解问题进行过数值方法研究.
本文考虑如下一类广义Rosenau-Kawahara方程初边值问题:
ut+uxxxxt+ux+uxxx-uxxxxx+(up)x=0,
x∈(xL,xR),t∈(0,T],
(3)
u(x,0)=u0(x),x∈[xL,xR],
(4)
u(xL,t)=u(xR,t)=0,
u(xL,t)x=u(xR,t)x=0,
u(xL,t)xx=u(xR,t)xx=0,t∈(0,T],
(5)
其中,p≥2为整数,u0(x)是一个已知的光滑函数.问题(3)~(5)具有如下守恒律[10-11]
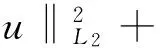
(6)
本文对问题(3)~(5)提出了一个3层线性差分格式,格式合理地模拟了问题的守恒量(6),且该格式是线性的,数值计算时不需要迭代,计算时间比较节约[12].
1 差分格式及其守恒律
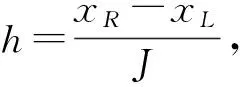
xj=xL+jh, 0≤j≤J,

在本文中记
|u-2=u-1=
u-0=uJ=uJ+1=uJ+2=0,
n=-2,-1,0,…,J,J+1,J+2},
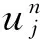
用C表示一般正常数(即在不同地方可以有不同的取值),并定义如下记号:
‖Un‖2=Un,Un,
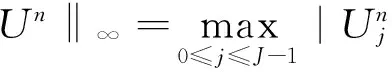

(7)
(8)
n=0,1,2,…,N,
(9)
差分格式(7)~(9)对守恒律(6)的数值模拟如下.
‖Un+1‖2+‖Un‖2+
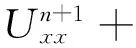
(10)
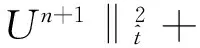
(11)
其中

由边界条件(9)和分部求和公式[12-15]得
=0,=0,
(12)
(13)
将(12)、(13)式带入(11)式后,递推即可得(10)式.
2 差分格式收敛性和稳定性
差分格式(7)~(9)的截断误差为
(14)
由Taylor展开,可知当h,τ→0时,
).
‖u‖L2≤C, ‖ux‖L2≤C,
‖uxx‖L2≤C, ‖u‖L∞≤C,
‖ux‖L∞≤C.
证明 由(6)式有
‖u‖L2≤C, ‖uxx‖L2≤C,
再利用Cauchy-Schwarz不等式有
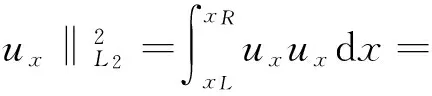
‖ux‖L2·‖uxx‖L2≤
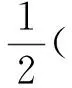
最后由Sobolev不等式得
‖u‖L∞≤C, ‖ux‖L∞≤C.
‖U‖≤C, ‖Ux‖≤C,
‖Uxx‖≤C, ‖U‖∞≤C,
‖Ux‖∞≤C.
证明 由定理1有
‖U‖≤C, ‖Uxx‖≤C,
再由分部求和公式[12-15]及Cauchuy-Schwarz不等式有
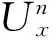
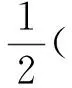
再由离散Sobolev不等式[16]得:
‖U‖∞≤C, ‖Ux‖∞≤C.
注 1 定理2表明,差分格式(7)~(9)的解Un以‖·‖∞无条件稳定.
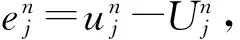
(15)
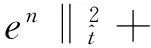

(16)
类似于(12)式有
=0,=0,
(17)
再由引理1,定理2以及Cauchy-Schwarz不等式有
=
(‖en-1‖2+‖en‖2+‖en+1‖2+
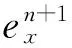
(18)
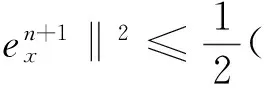
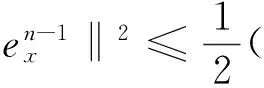
(19)
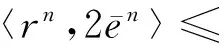
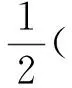
(20)
则将(17)~(20)式代入(16)式整理有
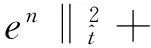

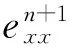
‖en‖2+‖en-1‖2).
(21)
令
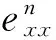
对(21)式两边乘以2τ,然后从1到N求和得
‖
先用两层的二阶方法(如C-N格式)先计算出U1,使之满足:B0=O(τ2+h2)2,又

‖rn‖2≤
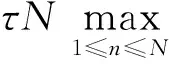
则由离散的Gronwall不等式[16]可得
BN≤O(τ2+h2)2,
即
‖eN‖≤O(τ2+h2),
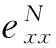
再由(19)式,可以推得

最有由离散Sovolev不等式[16]有
‖eN‖∞≤O(τ2+h2).
3 数值实验
对初边值问题(3)~(5)考虑p=3和p=5两种情形进行数值实验.当p=3时,方程(3)的孤波解[9-10]为
当p=5时,方程(3)的孤波解[9-10]为
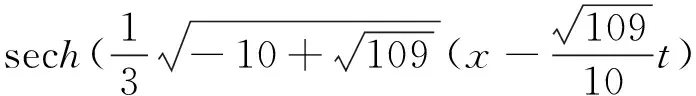
在计算中,取初值函数u0(x)=u(x,0),固定
xL=-80,xR=120,T=40.
就τ和h的不同取值对数值解和孤波解在几个不同时刻的误差见表1;格式对守恒量(6)的数值模拟见表2.
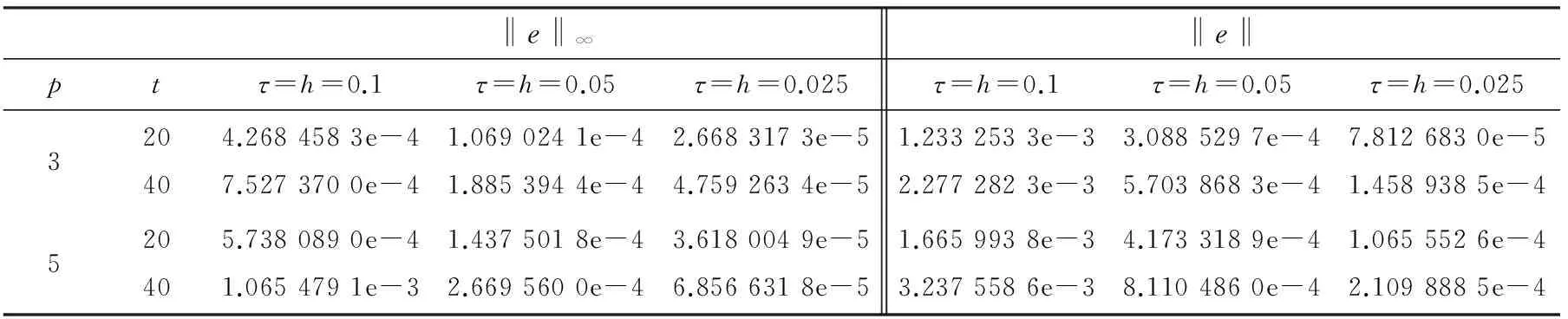
表 1 数值解和孤波解在不同时刻的误差

表 2 格式对守恒量En的数值模拟
从表1和表2可以看出,差分格式(7)~(9)明显具有二阶精度,且合理地模拟了守恒量(6),所以该格式是可靠的.
致谢 西华大学研究生创新基金(YCJJ2014033)对本文给予了资助,谨致谢意.
[1] Rosenau P. A quasi-continuous description of a nonlinear transmission line[J]. Physica Scripta,1986,34:827-829.
[2] Rosenau P. Dynamics of dense discrete systems[J]. Progress of Theoretical Physics,1988,79: 1028-1042.
[3] Park M A. On the Rosenau equation[J]. Applied Mathematics and Computation,1990,9(2):145-152.
[4] Omrani K, Abidi F, Achouri T, et al. A new conservative finite difference scheme for the Rosenau equation[J]. Appl Math Comput,2008,201(1/2):35-43.
[5] Chung S K. Finite difference approximate solutions for the Rosenau equation[J]. Appl Anal,1998,69(1/2):149-156.
[6] Chung S K, Pani A K. Numerical methods for the Rosenau equation[J]. Appl Anal,2001,77(3/4):351-369.
[7] Kim Y D, Lee H Y. The convergence of finite element Galeerkin solution for the Rosenau equation[J]. Korean J Comput Appl Math,1998,5(1):171-180.
[8] Zuo J M. Solitons and periodic solutions for the Rosenau-KdV and Rosenau-Kawahara equations[J]. Appl Math Comput,2009,215(2):835-840.
[9] Biswas A, Triki H, Labidi M. Bright and dark solitons of the Rosenau-Kawahara equation with power law nonlinearity[J]. Physics of Wave Phenomena,2011,19(1):24-29.
[10] 胡劲松,王玉兰,王正华. 广义Rosenau-Kawahar方程的孤波解及其守恒律[J]. 西华大学学报:自然科学版,2013,32(3):26-28.
[11] Hu J, Xu Y C, Hu B, et al. Two conservative difference schemes for Rosenau-Kawahara equation[J]. Adv Math Phys,2014,10(1):396-409.
[12] 刘倩,胡劲松,林雪梅. 带有阻尼项的广义SRLW方程的一个线性差分格式[J]. 四川师范大学学报:自然科学版,2014,38(2):199-202.
[13] 李思霖. 广义Rosenau-Burgers方程的有限差分近似解[J]. 四川师范大学学报:自然科学版,2013,37(4):595-598.
[14] 林雪梅,胡劲松,刘倩. 耗散SRLW方程的一个新的守恒差分逼近[J]. 四川师范大学学报:自然科学版,2014,37(1):49-53.
[15] 胡劲松,王玉兰,郑茂波. Rosenau-Burgers方程的一个新的差分格式[J]. 四川师范大学学报:自然科学版,2010,33(4):455-457.
[16] Zhou Y L. Application of Discrete Functional Analysis to the Finite Difference Methods[M]. Beijing:International Academic Publishers,1990.
2010 MSC:65N12; 65M12; 65N06
(编辑 陶志宁)
A Conservative Linear Difference Schemes of Generalized Rosenau-Kawahara Equation
CHEN Tao, HU Jinsong
(SchoolofScience,XihuaUniversity,Chengdu610039,Sichuan)
A linear three-level conservative difference scheme for the numerical solution of the initial-boundary value problem of generalized Rosenau-Kawahara equation is proposed. The difference scheme simulates two conservative quantities of the problem well.The prior estimation of the finite difference solution is obtained. It is proved that the finite difference scheme is convergent with second-order and unconditionally stable by discrete functional analysis method. Numerical experiments verify the theoretical results.
generalized Rosenau-Kawahara equation; finite difference scheme; conservation; convergence; stability
2014-06-29
四川省基础应用研究项目基金(2013JY0096)
O241.82
A
1001-8395(2015)06-0884-05
10.3969/j.issn.1001-8395.2015.06.018
*通信作者简介:胡劲松(1973—),男,教授,主要研究方向为微分方程数值解,E-mail:hjs888hjs@163.com

