圈闭评价中含油气性风险依赖性的概念、方法及应用
盛秀杰,金之钧,肖 晔,王义刚,蒋 瀚
(1.中国石化 石油勘探开发研究院,北京 100083;2.清华大学 理学院 数学科学系,北京 100084; 3.中国地质大学 信息工程学院,北京 100083)
圈闭评价中含油气性风险依赖性的概念、方法及应用
盛秀杰1,金之钧1,肖 晔2,王义刚1,蒋 瀚3
(1.中国石化 石油勘探开发研究院,北京 100083;2.清华大学 理学院 数学科学系,北京 100084; 3.中国地质大学 信息工程学院,北京 100083)
“至少有一个次级圈闭含有油气”的组合概率分析技术可评价圈闭的含油气性,评价结果反映了所有可能同时含有油气的圈闭组合形式。但受限于客观地质条件约束,有些圈闭是不应该同时出现的 —— 不同圈闭组合形式对资源量计算有直接影响。为了计算符合地质模型约束的圈闭组合概率,界定了次级圈闭的含油气性定量评价模型的地质涵义,指出次级圈闭含油气性评价本质上是遵循贝叶斯分析原则,包括边际概率和条件概率两部分评价内容,分别体现全局成藏和局部成藏的可能性。首先,强调不同圈闭成藏时会存在明显的地质相关性,单个层圈闭的评价是以全局成藏可能性为前提进行评价;其次,通过对应边际概率的可能取值范围,区分了“完全独立”、“部分决定”和“完全决定”3种不同含油气性风险依赖类型,而不同依赖类型直接决定了到底哪些圈闭组合才符合当前地质认识;最后,为油气资源一体化评价软件平台(PetroV)设计了一种改进的概率树分析技术,与不确定性体积法有机结合,实现了“基于含油气性风险依赖的概率组合加和”资源量计算方法。实例证明,要想获得较为客观的圈闭定量评价结果,需要充分考虑其所属不同次级圈闭间的含油气性风险依赖类型,并依此为基础才能给出对应合理地质模型解释的不确定性油气资源量分布结果。
概率组合加和;概率树;不确定性体积法;含油气性风险依赖;圈闭评价优选
客观评价油气发现概率,是区带、圈闭评价中地质评价的主要内容[1]。实际勘探经验表明,圈闭钻探的成功率(也称含油气发现概率)一般仅在40%左右,即使在地质认识程度相对较高的圈闭,事实证明,成功率也仅是在50%左右[2]。可见,采用符合地质模型的概率数学模型、基于最新勘探资料进行含油气性评价是主要地质研究活动[3-4]。不同概率数学模型的差异性取决于系列基本概率分析原则(表1)。①成功概率:单一地质事件发生的概率等于1减去其不发生的风险;②乘法原则(木桶原则): 独立地质事件间同时发生的概率等于每一地质事件发生概率的乘积;③加法原则:互斥地质事件同时发生的概率等于每一地质事件发生概率的和;④异或原则:独立地质事件间至少一个地质事件发生的概率等于各自不发生概率的乘积;⑤贝叶斯原则:条件概率用于计算一个地质事件在另外一个地质事件已经发生或已验证条件下的概率[5-6]。

表1 概率分析基本应用原则的公式列表与图示
表1中的乘法原则可分别应用于区带、次级圈闭的含油气性评价。考虑区带、圈闭的地质模型差异,在实际评价时存在遵循同一乘法原则但数学模型不同的特点。涵盖“生、储、盖、运、聚、保”各个环节,地质学家识别、定义区带或圈闭油气成藏缺一不可的地质条件(一般被定义为圈闭条件、充注条件、储层条件和保存条件),推断每一地质条件的主观成功概率,利用表1中的乘法原则给出区带或圈闭的含油气成功概率[7-8]。其中,区带的成藏地质条件对应的是同一区带内所有圈闭所经历的相同成藏地质条件(也称全局成藏条件),其数学模型本质是由系列全局成藏条件的边际概率相乘,计算联合概率来量化表达“区带某个地方至少有个油气藏存在”的可能性;某一圈闭的部分成藏地质条件对应的是全局成藏条件,部分地质条件对应的是仅仅与自身相关的局部成藏条件,其数学模型本质是体现贝叶斯原则的条件概率数学模型[9][式(1)]。公式(1)描述的是在全局成藏有利(也称区带含有油气)条件下圈闭含油气性的成功概率,在数学上其计算结果也被称之为非条件概率。便于下文分析描述,公式(1)中的①假定为圈闭条件,且是全局成藏条件;②假定为充注条件,且是全局成藏条件;③假定为储层条件,且是局部成藏条件;④假定为盖层条件,且是局部成藏条件。
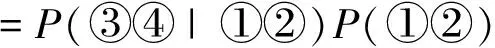
(1)
式中:P①,P②,P③,P④分别为圈闭的圈闭条件、充注条件、储层条件及盖层条件的成功概率,%;P含油气表示圈闭的含油气性成功概率,%;P边际概率表示全局成藏条件概率的乘积,%;P条件概率表示局部成藏条件概率的乘积,%,P非条件概率表示以边际概率为前提圈闭的含油气概率,%。
表1中的异或原则可应用于国内三(四)级圈闭的含油气性评价。由系列次级圈闭组成的三(四)级圈闭的含油气性评价模型,从单个圈闭遵循贝叶斯原则的条件概率数学模型衍变为不同圈闭遵循异或原则的组合概率数学模型[10][公式(2)]。理论上公式(2)的组合概率对应所有可能性的不同圈闭组合,实际上不是所有圈闭组合都有地质意义。不同圈闭组合意味着含油气概率及最终资源量计算结果相差很大,对后续的勘探开发决策方案有显著影响。本文通过剖析、明确公式(1)中边际概率的地质涵义,提出了不同次级圈闭间的含油气性风险依赖概念与类型,结合实际地质认识来落实“最有可能的圈闭组合”;在全新设计概率树算法的基础上,给出了不同风险依赖条件下的不同圈闭的组合概率计算方法,并结合实际区块进行了算法验证。
(2)
式中:P含油气表示某一四级或三级圈闭的含油气性成功概率,%;P群风险表示圈闭群地质风险,%;P所有个体风险表示圈闭个体地质风险,%;P边际概率表示全局成藏条件概率的乘积,%;P第i个条件概率表示第i个次级圈闭的条件概率。
1 含油气性风险依赖
1.1 定义
在分析系列三(四)级圈闭的沉积、构造等平面或剖面地质模型时(图1),地质人员常见的思路就是要识别出不同次级圈闭间可能相同的成藏过程,进而根据某一次级圈闭的钻后验证结果,推断其它圈闭的成藏地质条件是否成立[11]。如图1a,b中圈闭A没有发现储层,意味着圈闭B也不大可能发现储层;图1c中圈A闭的盖层条件好坏直接决定了圈B闭是否能够有效保存油气;图1d中的A和B两个圈闭位于同一油气运移路线上,B没有充注成功,意味着圈A闭的充注几率很低。由于不同次级圈闭经历了完全相同或相类似的油气成藏过程,意味着它们共享相同的成藏失败风险[公式(2)中的边际概率部分]:某一次级圈闭的含油气有无有可能会间接或直接反映其它层圈闭的含油气性有无。可见,三(四)级圈闭的含油气性评价应首先识别不同次级圈闭间的含油气性风险依赖关系,在充分考虑不同地质条件约束的前提下,计算“至少有一个次级圈闭含有油气”的含油气概率以及油气资源量。
1.2 依赖类型
不同地质模型下的全局成藏条件不同,意味着边际概率的地质涵义不同。公式(2)中,相同全局成藏条件的成功概率乘积表示边际概率(1-P群风险),局部成藏条件的成功概率乘积表示条件概率。以全局有利成藏条件作为前提(1-P个体风险),边际概率与条件概率的乘积量化表达了每个次级圈闭的含油气性评价结果,也称之为非条件概率[12]。边际概率的取值范围在单个圈闭含油气性成功概率最大值和1.0之间,体现了具有不同地质涵义解释的含油气性风险依赖关系。以图1b三角洲不同沉积亚环境间含油气性风险依赖分析为例,圈闭A和B有可能来自同一河道物源的沉积环境,也可能来自不同河道物源的沉积环境,揭示了储层条件是直接影响二者是否含有油气的全局成藏条件。假定圈闭A的含油气成功概率为0.3,圈闭B的含油气成功概率为0.2,根据储层是否来自同一河道物源以及沉积地理位置来分析二者之间可存在不同类型的含油气性风险依赖。
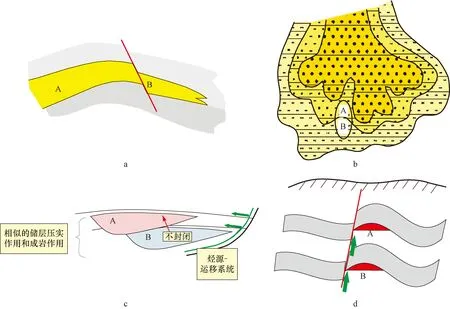
图1 常见的含油气性风险依赖地质模型Fig.1 Typical geological models of petroleum discovery risk dependency
1) 完全独立
圈闭A和B的储层来自不同河道的物源沉积环境,储层条件均很好,但在成藏过程中二者的储层形成没有直接联系,表示二者油气成藏过程各自独立[对应公式(2)中的共同成藏风险为0,边际概率值是1](图2a)。因此,边际概率等于1,等同地质上全局成藏条件可以被完全肯定,所有次级圈闭间的含油气性仅取决于自身局部成藏条件的好坏,互相之间几乎没有任何影响。
2) 部分决定(反之,部分依赖)
圈闭C和D的储层来自同一河道、同一物源沉积环境,二者储层形成几乎没有地理空间上的先后关系,储层条件应相同或类似,二者中任一储层的有无与好坏可间接反映另一次级圈闭的有无与好坏(图2b)。一般来说,最先发现油气的层圈闭应该是含油气性较高的次级圈闭,意味着圈闭D含有油气时,由于二者存在相同的全局储层条件,圈闭C发现油气的概率会明显提高。因此,边际概率值介于0.3(油气概率的最大值)和1.0之间,表示不同次级圈闭间具有部分类似或相同的全局成藏条件,含油气概率高的次级圈闭的含油气性部分决定了其它含油气概率较低的次级圈闭的含油气性。
3) 完全决定(反之,完全依赖)
圈闭E和F的储层来自同一物源沉积环境,但由于地理位置上的差异,圈闭E的储层形成应在圈闭F的储层形成之后(图2c)。从地质分析的角度,圈闭E的含油气性明显比圈闭F的含油气性成功的可能性要高,同时,如果圈闭E没有发现储层,则圈闭F肯定也不会发现储层。因此,边际概率值等于所有次级圈闭中含油气概率最大值(比如圈闭E),表示只有在圈闭E含油气性被证明的前提下,圈闭F才有被发现的机会,意味着圈闭E是否含有油气直接决定了圈闭F是否含有油气。

图2 3种含油气性风险依赖类型的地质模型示意图Fig.2 Geological demonstrations of three types of petroleum discovery risk dependency
1.3 概率组合加和
国内三(四)级圈闭资源量计算,基本上都是在假定其所属每个次级圈闭含油气概率为定值的前提下,片面地“简单加和”或“概率加权加和”所有次级圈闭的资源量[13]。“简单加和”获取的油气资源量很大程度上与实际地质情况并不吻合,代表了一种最为理想也是可能性最低的一种情况(每个圈闭都有油气是小概率事件),对后续勘探开发决策不可避免造成“高估”副作用。“概率加权加和”从多种可能性中局限性地选择了一种可能性,武断地将含油气概率与含油气物理体积混为一体,并不是地质模型本身的忠实反映——每一次级圈闭的物理体积不会因为其含油气概率的大小而发生改变。含油气性风险依赖类型对现有计算方法的改进在于:在充分考虑不同地质条件约束的情况下,到底是哪些圈闭组合才应该同时含有油气。本文在开发PetroV软件过程中,以单个圈闭的不确定性体积法为基础[14],考虑不同圈闭间的含油气性风险依赖类型,实现了一种区别于 “简单加和”或“概率加权加和”的“概率组合加和”算法。该算法本质上是对最新地质上识别出的、不可切分的次级圈闭进行符合不同地质条件约束的取样、组合,并在计算过程中充分考虑不同次级圈闭的“含油气体积”的不确定性来计算油气资源量分布。其中,油气资源量的不同分位值对应的就是各种可能的、有效的圈闭组合情况。如,当决定一定要先钻某一圈闭的情况下,可以根据“首钻目标”对其它圈闭的地质相关性,客观地给出“至少包含首钻目标”的不同评价对象的组合概率及资源量。此外,还可以回答“大于某油气资源量值的概率是多少”,“该资源量主要有哪些产层组成”,“分别贡献了多少”等勘探部署问题。
以图1a为例,A和B两个次级圈闭隶属同一储层形成环境而后经历同一构造运动(断层形成),储层条件和盖层条件对二者而言是全局成藏条件,盖层和烃源岩条件是局部成藏条件。考虑圈闭A储层的有无直接决定了圈闭B储层的有无,因此圈闭A和B间的含油气性风险依赖是典型的“完全决定”。展开公式(2),可分别计算圈闭A和B4种不同组合形式对应的含油气成功概率(表2);利用上述概率值和蒙氏模拟能够合理取样圈闭A和B,来计算对应的不确定性资源量分布(图3)。表2和图3的计算结果表明,“完全决定”意味着圈闭B单独出现的概率是0,由于圈闭A和B的概率相差无几,二者同时出现的概率大于圈闭A单独出现的概率;基于此“有偏”取样,不确定性资源量分布的不同分位值对应的主要是有圈闭A和B共同贡献,圈闭A单独贡献很少,圈闭B单独没有任何贡献,该计算结果与当前地质模型约束也是吻合的。
2 实例应用
以东营凹陷南斜坡八面河地区滩Ⅰ4个断块圈闭的资源量计算为例(图4中4块绿色区域)。该断块的烃源岩来自构造西北低洼部位的古近系孔(孔店组)二段,目的层位为中生界碎屑岩,盖层为上覆孔一段厚层泥岩。该断块的目的层来自于相同的沉积环境,油气充注也是以断层作为主要的运移通道,圈闭条件受断层和上倾地层决定,保存条件由区域厚层泥岩作为共同保障。相似的沉积环境(即,具有相似的储层条件)和相似的充注条件(即,均以断层为主要油气运移通道),是4个断块圈闭的全局成藏条件;由于所处构造位置高低不同,圈闭幅度大小各异,圈闭条件和保存条件是局部成藏条件。表3描述了4个断块圈闭均有可能获得勘探成功,但是成功的概率不同:1号断块地质成功的概率最大,为48.9%;4号断块地质成功的概率最小,为40.8%。由于储层条件相同,1号断块勘探成功与否对其他3个的成功率有一定影响 —— 1号断块是否含有油气决定了其他3个次级圈闭勘探的成功率。或者说,该勘探目标中勘探成功率较低的2号、3号和4号圈闭对成功概率较高的1号断块具有部分依赖性。

表2 圈闭的含油气组合概率计算(完全决定)
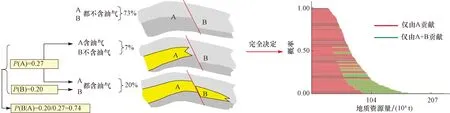
图3 “完全决定”的地质涵义与不确定性资源量计算结果示意图Fig.3 Geological meaning of the full risk dependence and corresponding resource evaluation results

图4 东营凹陷滩Ⅰ断块中生界顶层构造Fig.4 Top structural map of the Mesozoic in Tan Ⅰ fault block in the Dongying Depression
滩Ⅰ断块多层含油气概率的计算过程可用改进后的概率树模型表示(图5)。图中根节点的数字(0.68)

图5 部分决定时多层圈闭含油气概率树组合概率计算Fig.5 Combination probability tree calculation with partial dependency of multi-layer traps
表示部分决定情况下,整个勘探目标含有油气的边际概率,是全局成藏条件成功概率的乘积;分支节点上的数字表示不同断块圈闭含有油气或不含油气的条件概率。图5列出了4个断块圈闭在部分决定的情况下可能的圈闭组合概率。通过表4可推断,滩Ⅰ断块山发现油气的概率(至少一个断块圈闭发现油气的概率)
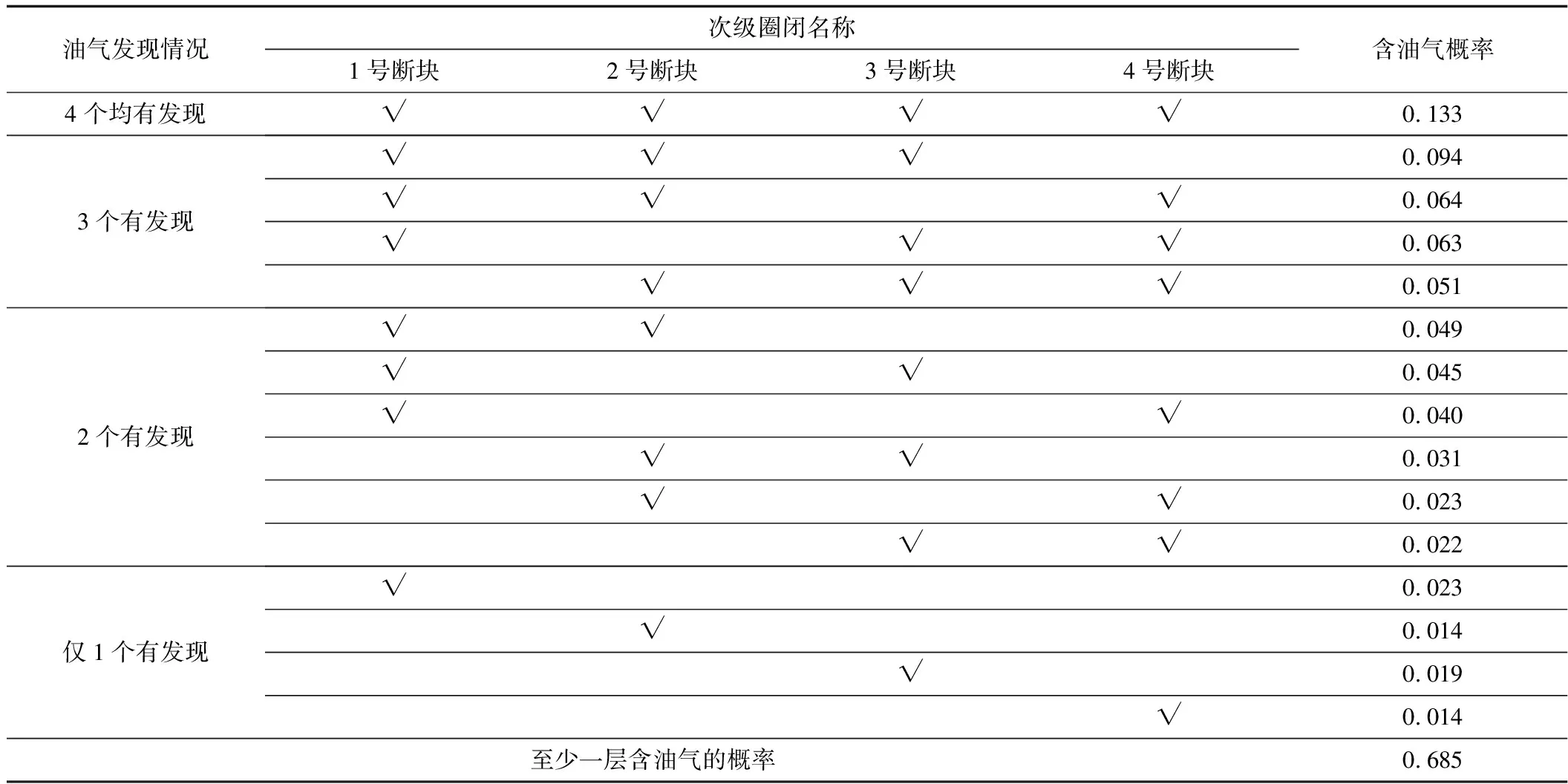
表4 部分决定时各圈闭油气发现的可能情况及各自发生的概率
注:√表示该圈闭有油气发现。
为68.5%,其他典型组合概率分别为:4层均有油气发现(概率为13.3%)、同时有3层发现油气(27.2%)、同时有2层发现油气(21.0%)及仅有1层发现油气(7.0%)。在部分决定的情况下,含油气概率较大的1号断块未发现油气时,其他含油气概率较低的3个层圈闭也可能发现油气,但它们单独组合出现的概率就小了很多,而伴随1号断块同时发现的组合概率比重明显偏大。
根据勘探成果及获得的相关地质参数,估算出滩Ⅰ断块山4个断块圈闭的可采资源量分别为:1号断块295×104t,2号断块8×104t,3号断块16×104t,4号断块57×104t。按文中提到的3种方法分别计算总资源量。①简单加和: 4个断块圈闭资源量的简单相加,资源量为376×104t;②概率加权加和:4个断块圈闭资源量的概率加权加和,资源量为178×104t;③概率组合加和:综合考虑4个断块圈闭之间的部分决定关系,通过蒙特卡洛模拟方法计算滩Ⅰ断块山平均可采资源量为270×104t。通过计算结果比较可以看出,简单加和法计算资源量结果偏大,概率加权加和法计算结果又偏小。而概率组合加和算法,在考虑了各断块圈闭的含油气概率和各断块圈闭之间的含油气性依赖关系的前提下,使多层资源量和含油气概率的计算结果更符合实际地质情况,其结果也更为可信。
3 结论
面向次级圈闭含油气性风险依赖定量评价技术,遵循的是贝叶斯概率分析原则;面向三(四级)圈闭含的含油气性评价遵循异或概率分析原则。在次级圈闭定量评价数学模型中,边际概率的大小取决于全局成藏条件的成功概率乘积,其大小刻画了不同含油气性风险依赖类型——不同依赖类型决定了不同次级圈闭以何种组合形式出现才符合客观地质条件约束。改进的概率树算法可以计算诸如“至少有一次级圈闭发现”、“多次级圈闭同时发现”等不同圈闭组合的概率,并能够直接给出是由哪些含油气次级圈闭组成。以改进的概率树为基础设计的“概率组合加和”资源量计算方法,在明确了哪些圈闭才应该同时出现的基础上,将其他不同地质条件约束有机融合到蒙氏模拟计算过程中,客观描述各个次级圈闭体积模型的不确定性。相较于经常采用的“简单加和”或“概率加权加和”算法,“概率组合加和”可获取更加符合当前地质模型的不确定性油气资源量计算结果,能够显著提升圈闭统一优选排队的合理性。
[1] Rose P R.Chance of success and its use in petroleum exploration[C]//Steinmetz R.The business of petroleum exploration:AAPG treatise of petroleum geology-Handbook of Petroleum Geology.Texas:AAPG,1992:71-86.
[2] Rose P R.油气勘探项目的风险分析与管理[M].北京:石油工业出版社,2002:6-50. Rose P R.Risk analysis and management of petroleum exploration ventures[M].Beijing:Petroleum Industruy Press,2002:6-50.
[3] 金之钧,张金川.油气资源评价技术[M].北京:石油工业出版社,1999:66-71. Jin Zhijun,Zhang Jinchuan.Petroleum resource assessment techniques[M].Beijing:Petroleum Industry Press,1999:66-71.
[4] 盛秀杰,金之钧,肖晔,等.成藏体系油气资源评价中的统计方法体系[J].石油与天然气地质.2013,34(6):829-830. Sheng Xijie,Jin Zhijun,Xiao Ye,et al.Statistical method series for the resource assessment of petroleum accumulation system[J].Oil & Gas Geology,2013,34(6):829-830.
[5] Bayarri M J,Berger J O.The interplay of Bayesian and frequentist analysis[J].Statist.Science,2004,19(2):58-80.
[6] Martinelli G,Eidsvik J.Bayesian networks for prospect analysis in the North Sea[J].AAPG Bulletin,2011,95(8):1423-1442.
[7] 金之钧,张金川.油气资源评价方法的基本原则[J].石油学报,2002,23(1):19-23. Jin Zhijun,Zhang Jinchuan.Fundamental principles for petroleum resource assessments[J].Acta Petrolei Sinica,2002,23 (1):19-23.
[8] 金之钧,张一伟,王捷,等.油气成藏机理与分布规律[M].北京:石油工业出版社,2003:50-172. Jin Zhijun,Zhang Yiwei,Wang Jie,et al.Hydrocarbon accumulation mechanisms and oil/gas distribution[M].Beijing:Petroleum Industry Press,2003:50-172.
[9] Lee P J.Statistical methods for estimating petroleum resources[M].Longdoug:Oxford University Press,2008:301-320.
[10] 吕鸣岗,朱向东,胡素云,等.圈闭/区带的地质风险分析[J].石油学报,1997,18(2):49-53. Lv Minggang,Zhu Xiangdong,Hu Suyun,et al.Geological risk analysis of trap and play[J].Acta Petrolei Sinica,1997,18(2):49-53.
[11] Otis R,Schneidermann N.A process for evaluating exploration prospects[J].AAPG Bulletin,1997,81(7):1087-1109.
[12] Crovelli R A,Balay R H.Analytic resource appraisal program for petroleum play analysis[J].Computer & Geoscience,1986,12(4B):423-475.
[13] 国土资源部油气战略研究中心.新一轮全国油气资源评价[M].北京:地质出版社,2009:66-71. Strategic Research Center of Oil & Gas Resources,Ministry of Land & Resources.The latest national petroleum resources assessment[M].Beijing:Geological Process,2009:66-71.
[14] Casella G,Robert C P.Monte carlo statistical methods[M].New York:Springer,2004:15-40.
(编辑 张亚雄)
Concept,method and application of geological risk dependency indicating petroleum discovery
Sheng Xiujie1,Jin Zhijun1,Xiao Ye2,Wang Yigang1,Jiang Han3
(1.PetroleumExploration&ProductionResearchInstitute,SINOPEC,Beijing,100083,China; 2.DepartmentofMathematicalScienceso,TsinghuaUniversity,Beijing100084,China;3.InformationEngineeringInstitute,ChinaUniversityofGeosciences,Beijing,100083,China)
The combination probability,the possibility that at least one segment contains hydrocarbons,can be used to assess the discovery probability of a trap.Obviously,‘at least one segment containing oil/gas’ reflects all possibilities of trap combinations.However,some traps should not be treated as one combination due to the constraint of special geological conditions.The trap combinations have direct influences on the estimation of geological resource.In order to calculate trap combination probability under the constraint of geologic models,this paper first cleared geological meaning of current evaluation model for segment and demystified its mysterious hype.It is in fact a classical Bayes mathematical model consisting of marginal and conditional probability,which quantifies separately the overall accumulation conditions or play-level and local accumulation conditions.Geological correlations do exist among different traps when hydrocarbons accumulate in them,thus the evaluation of single trap should be based on the prerequisite of possibility of overall hydrocarbon accumulation.Secondly,corresponding to the value range of marginal probability,this paper recognizes three geological risk dependence types including full independence,partial dependence and full dependence.These dependence types can directly determine which traps are concordant with current geologic knowledge.Finally,an improved probability tree technique was designed for the petroleum integrated assessment software (PetroV).When integrated with the non-deterministic volumetric method,it can realize resource volume estimation through ‘summation of probability combinations based on geological risk dependency’.Case study shows that geological risk dependence types play a key role in quantitative evaluation of traps and mapping of uncertain petroleum resource distribution corresponding to reasonable geologic model interpretations.
summation of probability combination,probability tree,undeterministic volumetric method,discovery risk dependence,trap assessment and target optimization
2014-03-19;
2014-12-20。
盛秀杰(1973—),男,高级工程师。E-mail:shengxj.syky@sinopec.com。
国家科技重大专项(2011ZX05005-001-004)
0253-9985(2015)01-0154-08
10.11743/ogg20150120
TE122.3
A

