神朔铁路轨道质量状态综合评定模型与算法研究
秦宪国,白 磊
(1.中国神华神朔铁路分公司,陕西榆林 719316;2.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
神朔铁路自陕西大柳塔镇至山西朔州市,正线全长265.75 km,是国家Ⅰ级电气化重载运煤专线铁路。神朔铁路是大秦铁路之后的第二条西煤东运大通道,2014年,神朔铁路日均开行112列,其中包含68列万t列车,每天运量78万t,运输任务繁重。若轨道等工务设备出现严重病害导致中断行车,将会给神朔铁路分公司造成巨大的经济损失。从2006年至2014年,神朔铁路的煤炭年运量与维修工作量(即平均每公里捣固量、平均每公里清筛量)的变化形态可以看出,神朔铁路维修工作量(或维修成本)随着煤炭年运量的逐年增加,基本呈现出逐渐上升的趋势。在神朔铁路煤炭运量逐年上升的前提下,有效控制养护维修成本对神朔铁路分公司具有重要意义。
轨道是铁路的主要技术装备,是铁路行车的基础,其作用是引导机车车辆运行,直接承受由车轮传来的荷载,并把它传布给路基和桥隧建筑物。轨道状态的好坏对铁路行车安全、乘客旅行舒适起着决定性作用。科学评价铁路轨道的综合状态对实现铁路运输安全畅通、养护维修成本的合理控制具有重要的意义。
根据《中国铁道百科全书——工程与工务》[1]中有砟轨道的定义,有砟轨道由钢轨、轨枕、道床、联结零件及防爬设备组成。神朔铁路的轨道类型是有砟轨道,故其轨道是由上述5大类设备构成。目前国内外既有研究成果多集中研究轨道内某种设备的某一类型病害的评定方法与劣化规律,如钢轨伤损病害[2]、轨道不平顺超限[3-4]等;或者研究轨道内某种设备病害(或超限)的综合评定,如轨道不平顺的综合评定[5]。而对轨道内5大类设备状态的综合评定研究较少。
然而,铁路设施设备状态劣化具有联动性[6],表现为同一里程位置(或同一里程范围内)铁路设施设备之间的劣化过程是相互影响的。若其中的一个设备出现病害或缺陷,往往会引起与其相关的设备出现病害或缺陷,如轨道扣件存在病害可能会严重影响轨道不平顺状态。因此,本文将利用基于主成分分析的K平均聚类算法(K-means Clustering Based on Principal Component Analysis,KM-PCA)对轨道内5大类设备的综合状态进行评定,辅助铁路管理部门科学地整体把握轨道健康情况。
1 轨道维修单元综合状态评定指标
作者出于以下几点分析,同时结合神朔铁路目前的维修养护能力和现场管理水平,提出将连续的轨道线路按照200 m的单元长度,划分成若干连续的轨道维修单元。一个轨道维修单元是该里程范围内钢轨、轨枕、道床、联结零件及防爬设备组成的集合体。轨道维修单元的综合状态由其里程范围内钢轨状态、轨枕状态、道床状态、联结零件状态及防爬设备状态共同确定。
1)不同里程处的钢轨、轨枕、道床、联结零件和防爬设备状态的劣化规律不同。
2)钢轨、道床为线形基础设施,适合分段研究其劣化规律。
3)轨枕、联结零件、防爬设备,若按照单个设备进行独立管理过于繁琐,也不符合神朔铁路工务现场管理的实际需求。
根据《铁路线路修理规则》(铁运[2006]146号)和神朔铁路实际管理现状,轨道设备的日常检查检测方式主要有人工线路检查、便携式添乘仪检测、机载式添乘仪检测、轨道检查车检测、钢轨探伤车检测、线路春秋检、人工巡道等。轨道不平顺状态、钢轨伤损状态主要依靠仪器进行检测,轨枕、道床、联结零件和防爬设备病害主要依靠人工肉眼进行检查。
通过上述这些轨道设备检查检测方式,神朔铁路工务部门通常仅用病害数、病害等级来粗略地把握设备状态,缺少对检查检测数据的深度分析。因此,作者基于可靠性、可用性、可维修性和安全性理论[7],提出利用病害数、病害率、病害重复度、病害集中度、病害变化率、失效率[8]、剩余寿命等状态评定指标对轨道单元状态进行多方位评价。其中,病害重复度是指轨道维修单元在给定时间范围内,相同类型、相同等级病害重复发生的次数;病害集中度是指轨道维修单元在给定时间范围单位长度空间发生的病害次数。在此基础上,为辅助神朔铁路工务管理部门综合掌控轨道维修单元状态、制定精准维修计划,本文提出轨道维修单元综合状态指数(TSCI,Track Segment Comprehensive Index),同时为符合工务部门基于阈值的养护维修工作流程,TSCI值定义为离散状态指标,每个TSCI离散指标值k∈(1,2,…,K),代表具有某种劣化特征的轨道维修单元簇。其计算公式为

式中:Qi为描述轨道维修单元某一侧面i的状态评定指标,其中i∈{1,2,…,I};f表示从一组状态评定指标Qi到综合指数TSCI的映射关系。
本文利用KM-PCA算法确定轨道维修单元的TSCI值,该算法将在第2节进行详细论述。
2 轨道维修单元KM-PCA算法建模
轨道维修单元状态评定指标用变量Q表示,Q=(Q1,Q2,…,QI)T,均值用 μ 表示,μ =E(Q),方差用 σ表示,σ=Var(Q)。通过对状态评定指标Q进行线性组合,得到相应的主成分 Z,Z=(Z1,Z2,…,ZI)T,其线性组合系数用 a 表示,a=(a1,a2,…,aI)T。则有
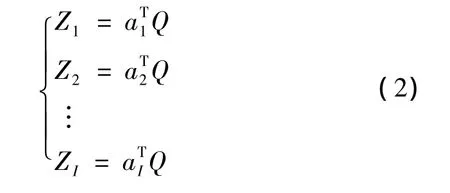

上述约束优化问题等价于求状态评定指标Q方差σ最大特征值对应的特征向量。假设方差σ的特征值用 λ1,λ2,…,λI表示,相应的特征向量用表示,即最优线性组合系数主成分 Zi的贡献率 ρi为,前k个主成分的累计贡献率ξk为,主成分Zi与状态评定指标Qi之间的相关系数为
假设前m个主成分的累计贡献率达到90%,即ξm≥90%。选择前m个主成分Z1,Z2,…,Zm作为新的描述轨道维修单元状态的属性变量。在此基础上,利用 K平均聚类算法(K-means Clustering)[9]对神朔铁路全线的轨道维修单元进行聚类分析。假设将轨道维修单元综合状态指数TSCI划分为K类,具体的聚类分析步骤如下:
1)在属性变量Zm构成多维空间中,随机选取K个簇中心 C1,…,Ck,…,CK。
2)分别计算每个轨道维修单元Ts(s∈S)到K个簇中心Ck的相异度,并将这些轨道维修单元分别划归到相异度最低的簇,如公式(4)所示。其中表示轨道维修单元Ts对应的簇为Ck。本文利用欧式距离定义Ts和Ck相异度。

3)根据聚类的结果,更新K个簇各自的中心,更新方法是取簇中所有轨道维修单元即各属性变量Zm的算术平均值。假设Ck簇中的轨道维修单元用Tks表述,用S'表示Ck簇中的轨道维修单元个数,则

4)重复2,3步骤,直到K个簇中心不发生改变。
3 实例运用
将神朔铁路正线划分为2 658个轨道维修单元。在本实例中,利用病害数、病害率、病害重复度、病害集中度和病害变化率5个状态评定指标构建轨道综合状态指数TSCI。基于2013年8月份神朔全线轨道维修单元13 290条状态数据,对本文提出模型的有效性进行验证。利用 R编程语言[10]实现对模型的构建和求解。
本实例确定出的轨道维修单元状态指标各主成分的贡献率和累计贡献率,如表1所示。由于前两个主成分的累计贡献率已经超过90%,故本实例选择第1、第2主成分作为新的描述轨道维修单元状态属性变量。

表1 轨道维修单元状态指标各主成分的贡献率和累计贡献率
第1、第2主成分Z1,Z2与轨道维修单元状态指标Q的相关系数a如表2所示。分析表2中的数据可知,第1主成分与Q1,Q2,Q3和Q4的相关系数均在0.94以上,与Q5的相关系数仅0.167,故该主成分主要衡量轨道维修单元各种病害数;第2主成分与Q5的相关系数在0.98以上,与其他状态评定指标的相关系数几乎为0,故该主成分主要衡量轨道维修单元病害的变化。

表2 轨道维修单元状态主成分与状态评定指标相关系数
基于KM-PCA算法的神朔铁路轨道维修单元聚类分析结果如图1所示。图中横坐标表示状态评定指标第1主成分,纵坐标表示第2主成分。通过分析图中数据可知,神朔全线的轨道维修单元划分为3类:第3类在图中用点表示,即TSCI=3,该类轨道维修单元的主要特征为病害数较多;第2类用点表示,即TSCI=2,该类轨道维修单元的主要特征为病害变化较快;第1类用点表示,即TSCI=1,该类轨道维修单元的主要特征为病害数少,病害变化不明显。

图1 神朔铁路轨道维修单元聚类结果
此外,若以第1主成分Z1、第2主成分Z2为基础变量,权重系数为各基础变量的贡献率,则可构造出一个连续的轨道维修单元综合状态评定指标。将轨道维修单元综合状态由差到好排序,即按该指标从大到小进行排序,前5个综合状态较差的轨道维修单元如表3和图2所示。神朔铁路工务管理部门依据表3中的数据,结合日常管理经验,可较准确地确定全线重点薄弱地段。这有助于工务管理部门根据自身的维修能力,制定合理的维修作业计划,合理使用维修资源,实现神朔铁路运输安全和节省养护维修成本。此外,从图2可看出,综合状态较差的前5个轨道维修单元主要集中在TSCI=3的轨道维修单元簇中,因此工务管理部门在日常生产活动中需对TSCI=3的轨道维修单元簇进行重点检查、监控。

表3 神朔铁路前5个综合状态较差的轨道维修单元

图2 神朔铁路前5个综合状态较差的轨道维修单元分布
4 结论
本文提出按照200 m的基本长度,将神朔轨道线路划分为若干轨道维修单元,并建议神朔铁路工务部门有关轨道设备的日常检查、维修均以轨道维修单元为对象。
利用钢轨、轨枕、道床、联结零件和防爬设备状态数据,构建多种状态评定指标对轨道维修单元进行多方位评价。同时,基于这些状态评定指标,利用KM-PCA算法确定轨道维修单元综合状态指数TSCI。工务管理部门可通过分析TSCI,有效确定神朔全线的重点薄弱地段,为制定精准养护维修计划提供决策支持。
在今后的研究中,可尝试构建出更多的状态评定指标对轨道维修单元进行聚类分析。本文研究成果也可进一步整合到铁路工务安全风险管理信息系统中,辅助神朔铁路工务管理部门全面控制轨道安全风险。
[1]中国铁道百科全书编辑委员会.中国铁道百科全书——工程与工务[M].北京:中国铁道出版社,2004.
[2]LIU X,LOVETT A,DICK T,et al.Optimization of Ultrasonic Rail-Defect Inspection for Improving Railway Transportation Safety and Efficiency[J].Journal of Transportation Engineering,2014,140(10):401-408.
[3]KHOUY I A,LARSSON-KRALK P O,NISSEN A,et al.Optimisation of Track Geometry Inspection Interval[J].Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2014,228(5):546-556.
[4]BAI L,LIU R,SUN Q,et al.Markov-based Model for the Prediction of Railway Track Irregularities[J].Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,2015,229(2):150-159.
[5]康熊,王卫东,刘金朝.基于RAMS的高速铁路轨道平顺状态综合评价体系研究[J].中国铁道科学,2013,34(2):13-17.
[6]王峰,刘仍奎.高速铁路网格化管理理论与实现技术[M].北京:中国铁道出版社,2014.
[7]British Standards Institution.EN 50126—1999 Railway Applications:the Specification and Demonstration of Reliability,Availability,Maintainability and Safety[S].London:British Standards Institution,1999.
[8]JOLLIFFE I.Principal Component Analysis[M].Hoboken:Wiley Online Library,2002.
[9]HARTIGAN J A W.Algorithm AS 136:A K-Means Clustering Algorithm[J].Journal of the Royal Statistical Society.Series C(Applied Statistics),1979,28(1):100-108.
[10]R Core Team.R:A Language and Environment for Statistical Computing[EB/OL].(2014-03-30)[2014-04-09].http://www.R-project.org.

