双面冷却环形燃料元件的几何尺寸优化

邓阳斌，巫英伟,*，张伟旭，田文喜，张大林，苏光辉

(1.西安交通大学 动力工程多相流国家重点实验室，陕西 西安 710049；2.西安交通大学 机械结构强度与振动国家重点实验室，陕西 西安 710049)



双面冷却环形燃料元件的几何尺寸优化

邓阳斌1，巫英伟1,*，张伟旭2，田文喜1，张大林1，苏光辉1

(1.西安交通大学 动力工程多相流国家重点实验室，陕西 西安 710049；2.西安交通大学 机械结构强度与振动国家重点实验室，陕西 西安 710049)

针对双面冷却环形燃料元件，建立了计算元件内流量分配、温度场分布和径向最高温度位置沿元件轴向分布的相关数学物理模型，编制了热工水力计算程序，制定了评估环形燃料元件几何设计优劣性的3个评价指标，获得了双面冷却环形燃料元件的最优尺寸设计范围。计算结果表明，优化后的环形燃料元件具有良好的热工水力特性，优化后的几何尺寸与麻省理工学院选择的尺寸吻合良好，验证了程序的可靠性和正确性。

双面冷却环形燃料元件；几何尺寸优化；流量分配；内外冷却平衡

双面冷却环形燃料元件相对传统棒状燃料元件具有两个优势：1) 减小了芯块径向热传导路径的厚度，显著降低了芯块内最高温度；2) 增加了冷却剂润湿周长，冷却能力得到显著提高[1-3]。麻省理工学院(MIT)[4]的研究表明，在压水堆中使用这种燃料，功率密度可提高到150%，同时保持甚至提高安全裕量。2001年，MIT提出将双面冷却环形燃料元件应用于压水堆的设想，并启动了相关研究[5]。此后，美国将环形燃料作为新一代压水堆燃料及核电厂延寿优先燃料进行研发，韩国也计划采用环形燃料对在运行的OPR-1000进行技术改造[6]。2010—2011年，中国原子能科学研究院开发了环形燃料设计与分析软件，开展了环形燃料元件应用于压水堆核电厂的可行性研究[7-8]。目前，国内外学者针对双面冷却环形燃料的研究多为定性的综述性研究。虽然针对组件排列方式做了较多研究[9]，但类似本文开展的燃料元件几何尺寸优化设计的研究较少，具体的模型和计算方法尚未见文献报道。本文通过独立建立相关物理数学模型和燃料元件性能评价指标，对环形燃料元件几何尺寸进行优化研究。

1 双面冷却环形燃料元件的几何尺寸优化原理

1.1 几何结构

图1 燃料元件横截面示意图Fig.1 Cross section diagram of fuel element

环形燃料元件主要由内外两层包壳和圆环状的UO2芯块组成，内外包壳与芯块之间都存在一定的气隙。冷却剂可同时从内外两个通道对燃料元件进行冷却，其中外通道可与周围的通道进行质量、动量和能量交换，而内通道由于与外界隔离，故与外界无质量、动量和能量交换。图1为双面冷却环形燃料元件和实心棒状燃料元件横截面示意图。

1.2 几何尺寸优化原理

双面冷却环形燃料元件的尺寸设计，在中子物理学上主要考虑栅元的“水-铀”体积比，本研究将保持该比值与传统压水堆中的值基本相等。在热工水力学上必须考虑的一个因素是内外通道冷却能力的平衡：若环形芯块中心孔直径过小，则内通道将因冷却剂流量过小导致冷却能力不足；反之，元件内径过大会导致外通道冷却能力不足。这将导致内通道或外通道出口处冷却剂温度不能满足冷却剂出口所需要的过冷度，甚至在靠近出口发生饱和沸腾。如果环形芯块的中心孔大小取值合适，使内外通道的冷却达到平衡，便可有效地利用冷却剂对燃料元件进行充分的冷却。本研究主要基于内外通道冷却平衡原理，对环形燃料元件的尺寸进行优化设计。

1.3 尺寸优化的评价指标

为评估环形燃料元件尺寸设计优劣，本研究制定了3个评价指标：

1) 内外通道出口处冷却剂温差：内外通道冷却越平衡，内外通道出口处冷却剂温差越小，说明冷却剂得到了更高效的利用，因此冷却剂出口处温差可作为评价内外冷却平衡度的定量指标；

2) 芯块最高温度：芯块最高温度作为燃料元件设计的一个重要参数，与燃料元件安全性能有着密切的关系，其大小直接体现了燃料元件性能的优劣；

3) 径向最高温度位置偏离度：径向最高温度位置偏离芯块几何中心越小，即元件温度场分布对称性越好，说明燃料受到的冷却越充分，且对燃料元件的机械性能越有利。

2 数学物理模型

2.1 压降与流量分配模型

内外通道流量分配的基本原理是压降相等，本研究根据流道形状和流动特点，仅考虑重力压降和摩擦压降。此外，尽管环形燃料元件内外通道为并联平行通道，但相关研究表明并不存在流动不稳定性问题[10]。

重力压降Δpel(Pa)为：

(1)

摩擦压降Δpf(Pa)计算采用Darcy公式：

(2)

其中：l和De分别为流道长度和当量直径，m；v为流体速度，m/s；ρ、g和θ分别为流体密度、重力加速度和流道与水平面夹角；f为摩擦因子，在不同的流动条件和流动状态下取值不同，元件中冷却剂基本处于单相充分发展紊流，故本研究采用McAdams关系式计算f：

(3)

式中：μ为动力黏度，kg/(m·s)；Re为雷诺数。

2.2 冷却剂温度场分布模型

冷却剂的温度场计算属于热输运计算，根据热平衡原理，冷却剂温度计算公式如下：

(4)

式中：T(z)为轴向位置z处的冷却剂温度，K；Tin为冷却剂的进口温度，K；q″(z)为z高度处面积释热率，W/m2；cp为冷却剂的比定压热容，J/(kg·K)；G为冷却剂的质量流速，kg/s。

冷却剂焓计算公式为：

(5)

其中：h(z)和hin分别为z高度处和进口处冷却剂焓，J/kg；Q(z)为进口到z处的累积功率，W；W为质量流量，kg/s。

2.3 对流换热模型

冷却剂和包壳外表面间存在对流换热，此换热使用牛顿冷却定律进行计算：

(6)

(7)

式中：Tcs(z)和ΔT(z)分别为z高度处包壳外表面温度和对流换热温差，K；hcs为换热系数，W/(m2·K)。

单相流动换热系数hcs由Dittus-Boelter公式计算，考虑到可能出现的沸腾现象，采用Chen关联式[11]计算两相流动换热系数：

(8)

(9)

式中：λcs为冷却剂的导热系数，W/(m·K)；Pr为普朗特数；F和S分别为雷诺数因子和泡核沸腾抑制因子；ρg和ρf分别为气相和液相密度，kg/m3；hfg为汽化潜热，kJ/mol；k为导热系数，W/(m·K)；kf为流体的导热系数，W/(m·K)；μf为流体的动力黏度，kg/(m·s)；x为质量含气率；Tw-Ts为壁面过热度，K；σ为液体的表面张力，N/m；cpf为流体的比定压热容，J/(kg·K)；pw为流体处于壁面温度时的饱和压力，Pa；ps为流体的实际压力，Pa。

2.4 包壳导热模型

包壳导热视为无内热源的导热问题，计算公式为：

(10)

其中：Tci(z)为轴向z处的包壳内表面温度，K；ql(z)为轴向z处的线功率密度，W/m；dci和dcs分别为包壳内、外径，m；kc为包壳导热系数，W/(m·K)，其值随温度变化，本研究采用平均温度对应的导热系数进行迭代计算。

2.5 气隙换热模型

燃料芯块与包壳内表面的传热存在3种形式：间隙换热、辐射换热和固体接触导热。环形燃料元件温度较低，辐射换热可忽略不计，且仅当燃耗深度很大时才会出现气隙闭合，故本程序只考虑间隙换热。间隙换热认为气隙静止不动，将其视为固体导热处理，计算公式如下：

(11)

气隙中的气体导热系数采用下式计算：

(12)

式中：Tu(z)为轴向z处燃料表面温度，K；du为燃料芯块直径，m；T为气体热力学温度，K；A1、B1为实验常数[12]。

2.6 芯块温度场计算模型

1) 径向最高温度位置的计算

径向最高温度位置的确定采用解析法进行计算。将傅里叶导热定律应用于半径为r的芯块微元环中，则有：

(13)

式中：ku(t)为温度t时燃料的导热系数，W/(m·K)；qv为体积释热率，W/m3；ro为绝热处半径，m。

对式(13)两端进行积分并整理，推导出环形燃料芯块的积分热导率：

(14)

式中，下标u表示芯块表面处的参数，将式(14)变形可得：

(15)

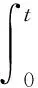
假设芯块最高温度出现在径向ro处，分别从燃料元件内、外表面出发，由外往内计算，可分别得到ro处燃料温度的表达式，这两个表达式必须相等，据此可反解出ro：

ro=

(16)

式中，带下标o、u1和u2的分别表示径向最高温度、芯块内表面和芯块外表面位置处对应的参数。

2) 芯块温度场的计算

燃料芯块温度场的计算采用数值法进行求解，图2为节点划分示意图。

图2 节点划分示意图Fig.2 Nodes meshing diagram

由能量守恒可得：

(17)

式中：T为燃料温度；x为径向坐标；S为内热源；n为传热表面的法向方向。

由图2可知，径向第m个节点与其相邻节点间的关系为：

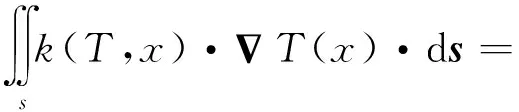
(18)

(19)

联立式(17)～(19)，整理后可得下列形式代数方程：

(20)

系数am、bm、cm和dm表达式如下：

(21)

上述线性代数方程组联立芯块内外表面处的边界条件，可由三对角追赶法进行求解。

3 程序编制及求解

3.1 程序编制

如图3所示，对研究对象进行控制体划分，计算节点取在相邻控制体间的界面上。

图3 燃料元件控制体划分Fig.3 Control volume meshing of fuel element

以Fortran 90为工具，编制程序求解上述数学物理模型。本程序能较为完整地模拟双面冷却环形燃料元件的热工水力性能，图4为程序求解流程图。

图4 程序求解流程图Fig.4 Flow diagram of code calculation

3.2 研究对象及初始参数

基于MIT的研究成果[9](环形燃料元件应用于压水堆时，堆芯大小不变，组件大小不变，组件改为13×13排列，反应堆功率提升到150%，冷却剂进口温度降低10 ℃，冷却剂流量提升至130%)，本研究为程序计算选取的初始参数列于表1。

表1 环形燃料元件初始参数Table 1 Original parameter of annular fuel element

4 结果及分析

4.1 冷却剂和包壳温度

图5为不同几何尺寸设计下燃料元件内外通道冷却剂及内外包壳温度分布。从图5a可看出，当燃料元件内通道直径较小时，内通道的冷却剂和包壳温度明显高于外通道对应值，在内通道靠近出口处甚至出现沸腾现象。图5b表明，当燃料元件内径较大时，情况与图5a恰好相反，出现此现象的原因是内通道直径过大或过小都会引起内外通道冷却剂分配的失衡。而图5c表明，当燃料元件内径大小合适时，内外通道冷却剂及包壳表面温度基本相等，内外均不会出现沸腾换热，具有较好的内外通道冷却平衡。

燃料元件内径：a——7.0 mm；b——10.0 mm；c——8.5 mm

4.2 径向最高温度位置

图6为不同几何尺寸设计下燃料元件径向最高温度位置偏离芯块几何中心的情况。其中，横坐标值的正、负分别代表往外、内通道偏离。图6显示出4个规律：1) 进口处所有尺寸设计下最高温度线均往内通道偏离，这是因为外通道的润湿周长大于内通道，故外通道冷却能力强于内通道；2) 从进口到出口过程中，内径小的最高温度位置逐渐向内通道偏，而内径大的最高温度位置逐渐向外通道偏，这是因为内径过小时，内通道冷却剂温度高于外通道，导致内通道冷却能力低于外通道，反之情况相反；3) 越靠近出口，最高温度位置线向内或向外偏离越严重，这是因为越靠近出口处，内外通道冷却剂温差越大(图5)，导致内外通道冷却越不平衡；4) 若元件内径选择合适，内外通道冷却剂从出口到进口都近似相等(图5b)，冷却剂最高温度线将在高度方向上保持近似直线(图6中内径为8.6 mm的曲线)。

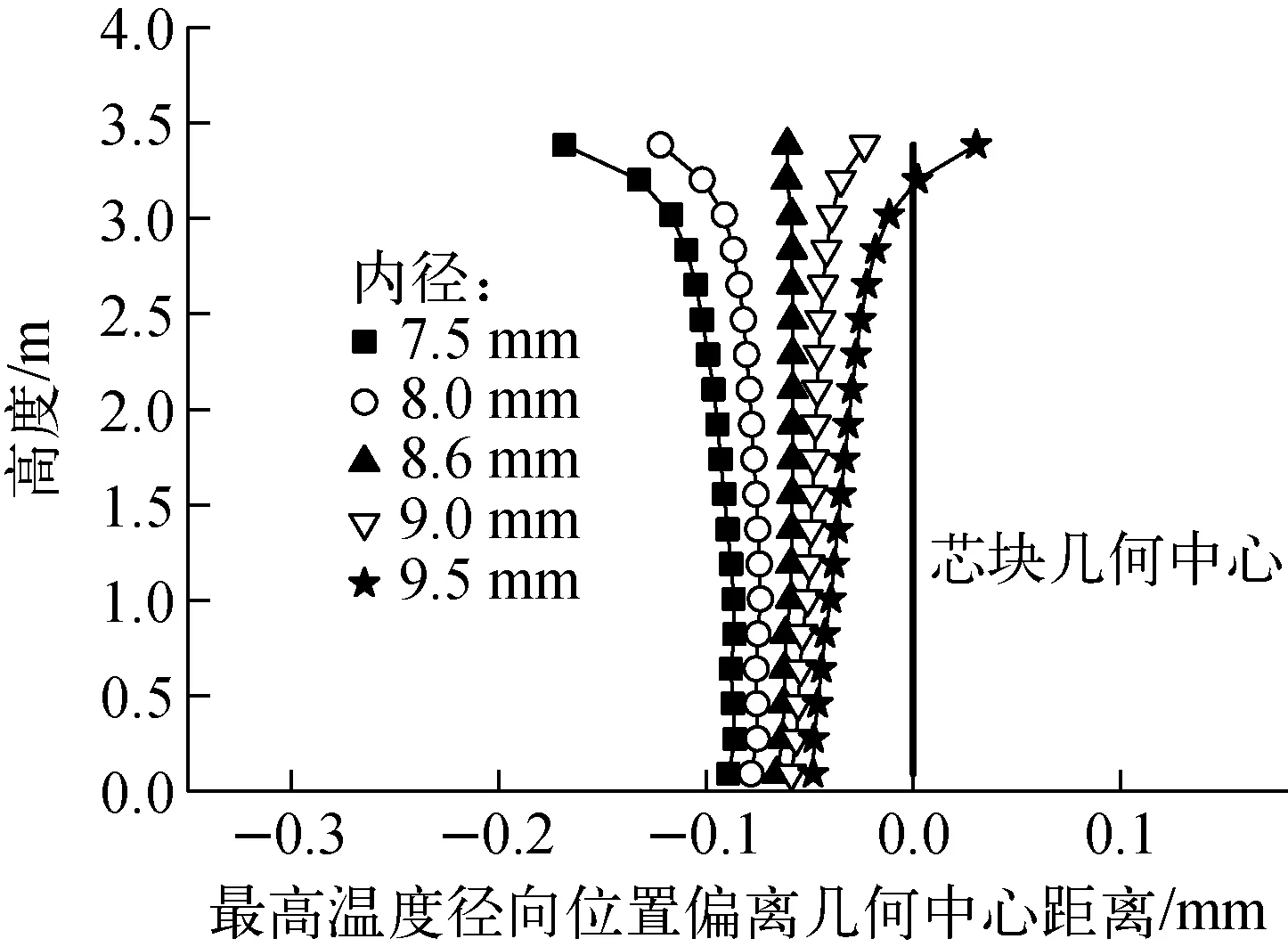
图6 径向最高温度位置分布Fig.6 Position distribution of radial maximum temperature

4.3 几何尺寸优化选择

图7为不同几何尺寸下环形燃料元件对应的3个评价指标，图中两条虚线为饱和沸腾分界线，仅在两虚线间的区域不会发生饱和沸腾。

图7 3个评价指标Fig.7 Three evaluation indexes

综合考虑3个评价指标，选择燃料元件内通道直径为8.5～8.75 mm，理由如下：

1) 内外通道出口处冷却剂温差：该温差越小说明内外通道冷却越平衡，从图7可看出,内径在8.5～8.75 mm范围时冷却剂出口温差不超过5 K；

2) 最高温度线偏离中心线程度：理论上最高温度线越接近几何中心，芯块得到的冷却越充分，由图7可知，内径为8.5～8.75 mm时的偏离量不超过50 μm；

3) 芯块最高温度：如图7所示，最高温度随燃料元件内径的增大而减小，这是因为燃料体积一定时，元件内径增大，燃料芯块变“薄”，且内外润湿周长变大，理论上最高温度越小越好，但元件内径过大时，内外冷却出现明显的不平衡，内径在8.5～8.75 mm范围时的最高温度不超过1 200 K，已远低于传统棒状燃料，因此是比较理想的选择。

根据燃料体积、包壳厚度和气隙宽度保持不变，由选择的元件内径即可确定元件径向所有尺寸。

4.4 优化结果对比

图8为几何尺寸优化后，环形燃料元件在不同线功率密度下的径向温度分布。由图8可知，尺寸优化后，环形燃料元件具有燃料温度低、径向温度分布对称度高等良好的热工水力性能。

图8 环形燃料元件径向温度分布Fig.8 Radial temperature distribution of annular fuel element

表2为环形燃料元件几何尺寸优化结果和MIT选择尺寸[9]的对比。从表2可看出，本研究的结果和MIT选择的尺寸吻合较好，初步验证了本程序计算的正确性和可靠性。

表2 优化结果与MIT选择尺寸对比Table 2 Comparison of optimization results and MIT selected sizes

5 结论

本研究通过独立建立相关的物理数学模型，开发了双面冷却环形燃料元件热工水力计算程序，并制定了3个性能评价指标，对双面冷却环形燃料元件进行了几何尺寸优化。主要结论如下：

1) 综合考虑3个评价指标，确定了最优燃料元件尺寸设计范围：内包壳内径，0.850 0～0.875 0 cm；内包壳外径，0.964 3～0.989 3 cm；芯块内径，0.976 7～1.001 7 cm；芯块外径，1.400 7～1.418 2 cm；外包壳内径，1.413 1～1.430 6 cm；外包壳外径，1.527 4～1.544 9 cm。

2) 几何尺寸优化后，环形燃料元件表现出了良好的热工水力性能；优化结果与MIT选择尺寸高度吻合，证明了程序计算的正确性和可靠性。

[1] BLINKOV V N, BOLTENKO E A, ELKIN I V, et al. Prospects for using annular fuel elements in nuclear power engineering[J]. Thermal Engineering, 2010, 57(3): 213-218.

[2] FENG B. On the use of high performance annular fuel in PWRs[D]. US: Massachusetts Institute of Technology, 2008.

[3] SHIN C H, CHUN T H, OH D S, et al. Thermal hydraulic performance assessment of dual-cooled annular nuclear fuel for OPR-1000[J]. Nuclear Engineering and Design, 2012, 243: 291-300.

[4] FENG D, MORRA P, SUNDARAM R, et al. Safety analysis of high-power-density annular fuel for PWRs[J]. Nuclear Technology, 2007, 160(1): 45-62.

[5] HEJZLAR P, DRISCOLL M J, KAZIMI M S. High performance annular fuel for pressurized water reactors[J]. Transactions of the American Nuclear Society, 2001, 84: 192-204.

[6] SONG K W, KIM K S. Feasibility evaluation report of dual-cooled annular fuel[R]. Korea: KAERI, 2009.

[7] 季松涛，何晓军，张爱民，等. 压水堆核电站采用环形燃料元件可行性研究[J]. 原子能科学技术，2012，46(10)：1 232-1 236.

JI Songtao, HE Xiaojun, ZHANG Aimin, et al. Study on feasibility of annular fuel applied in PWR nuclear power plant[J]. Atomic Energy Science and Technology, 2012, 46(10): 1 232-1 236(in Chinese).

[8] 杨维波，薄美芳. 核电厂采用环形燃料经济性分析研究报告，KY·DG·HK 1002-18-RJ[R]. 北京：中国核电工程有限公司，2011.

[9] HEJZLAR P, KAZIMI M S. Annular fuel for high-power-density pressurized water reactors: Motivation and overview[R]. US: Massachusetts Institute of Technology, 2006.

[10]FENG D, HEJZLAR P, KAZIMI M S. Thermal-hydraulic design of high-power-density annular fuel in PWRs[J]. Nuclear Technology, 2007, 160(1): 16-44.

[11]CHEN J C. Correlation for boiling heat transfer to saturated fluids in convective flow[J]. Industrial & Engineering Chmistry Process Design and Development, 1966, 5(3): 322-328.

[12]于平安，朱瑞安，喻真烷，等. 核反应堆热工分析[M]. 上海：上海交通大学出版社，2002.

Geometric Size Optimization of Dual-cooled Annular Fuel Element

DENG Yang-bin1, WU Ying-wei1,*, ZHANG Wei-xu2,TIAN Wen-xi1, ZHANG Da-lin1, SU Guang-hui1

1.StateKeyLaboratoryonPowerEngineeringandMultiphaseFlow,Xi’anJiaotongUniversity,Xi’an710049,China; 2.StateKeyLaboratoryforStrengthandVibrationofMechanicalStructures,Xi’anJiaotongUniversity,Xi’an710049,China)

Based on the design of dual-cooled annular fuel elements, relevant mathematical and physical models were established to calculate the flow distribution, temperature field distribution and distribution of radial maximum fuel temperature positions along the axial direction, and a thermal-hydraulic calculation code was developed. Three evaluation indexes were independently proposed to evaluate geometric designs of dual-cooled annular fuel elements, and the ranges of optimal element sizes were obtained. Calculation results show that the optimized dual-cooled annular fuel element presents good thermal-hydraulic performance. The optimized geometric sizes agree well with those obtained by Massachusetts Institute of Technology, which demonstrates the code reliability and accuracy.

dual-cooled annular fuel element; geometric size optimization; flow distribution; inner and outer cooling balance

2014-04-01;

2014-06-12

中央高校基本科研业务费专项资金资助项目(XJJ2012114)；国家国际科技合作专项资助(2012DFG61030)

邓阳斌(1991—)，男，江西赣州人，硕士研究生，核能科学与工程专业

*通信作者：巫英伟，E-mail: wyw810@mail.xjtu.edu.cn

TL333

A

1000-6931(2015)07-1208-07

10.7538/yzk.2015.49.07.1208