鲁棒的基于均值漂移的自适应卡尔曼滤波目标跟踪
李小和,屈 展,王魁生
(西安石油大学 计算机学院,陕西 西安 710065)
鲁棒的基于均值漂移的自适应卡尔曼滤波目标跟踪
李小和,屈 展,王魁生
(西安石油大学 计算机学院,陕西 西安 710065)
提出了一种鲁棒的基于均值漂移的自适应卡尔曼滤波目标跟踪算法。首先建立卡尔曼滤波的系统模型,用卡尔曼滤波预测目标在当前帧的位置,并将该预测值作为初始值,用均值漂移算法搜索目标位置。然后将搜索结果作为观测值来修正预测值,并根据目标模型与由均值漂移算法搜索得到的候选目标模型及相应背景模型的Bhattacharyya系数自适应调整卡尔曼滤波的参数,从而提出了一种鲁棒的自适应卡尔曼滤波目标跟踪算法。仿真实验表明,该算法具有较好的跟踪精度,对遮挡具有较强的鲁棒性。
目标跟踪;卡尔曼滤波;均值漂移;AKF算法;鲁棒性
近年来均值漂移(MS)算法[1]被广泛应用于目标跟踪领域[2-9]。文献[2]提出了一种MS目标跟踪算法,计算简单快捷,且具有实时性。该算法要求相邻两帧目标位置必须有重叠,因此,当目标的运动速度较小时,能够得到比较理想的跟踪效果,而当目标运动速度较快或目标较小导致相邻两帧的目标位置没有重叠时,无法有效跟踪目标。
为了进一步提高MS目标跟踪算法的鲁棒性,在当前帧,可先用卡尔曼滤波(KF)算法[10]预测目标的位置,然后将KF的预测值作为初值,用MS算法搜索目标的位置[5-7]。虽然该方案在一定程度上提高了跟踪算法的鲁棒性,但是当目标被遮挡时无法有效跟踪目标。文献[8]通过在目标区域采用多个MS模型解决部分遮挡问题。文献[9]通过目标模型与由MS算法确定的候选目标模型的Bhattacharyya系数自适应调整KF算法的参数,从而提出了一种自适应卡尔曼滤波(AKF)目标跟踪算法。AKF算法在目标运动速度较快或目标被遮挡时,能够有效跟踪目标。
虽然AKF算法对遮挡具有较好的鲁棒性,但是当目标被具有与目标相似特征的物体遮挡时无法有效跟踪目标。为了克服以上不足,本文首先用KF预测目标在当前帧的位置,并将预测值作为初值,用MS算法搜索目标的位置。然后将搜索结果作为观测值修正预测值,并根据目标模型与MS算法确定的候选目标模型及相应背景模型的Bhattacharyya系数自适应调整KF算法的参数,从而提出了一种鲁棒的自适应卡尔曼滤波(RAKF)目标跟踪算法。仿真实验表明,该算法具有较好的跟踪精度,对遮挡具有较强的鲁棒性。
1 均值漂移目标跟踪
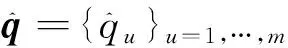
(1)
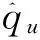
目标模型与候选目标模型的Bhattacharyya系数为
(2)
(3)
式中:g(x)=-k′(x);
(4)
从y0开始,迭代式(3)直至收敛,从而实现目标的跟踪。关于MS目标跟踪算法的详细论述请参阅文献[2]。
2 鲁棒的自适应卡尔曼滤波目标跟踪
本文提出的基于MS的RAKF算法首先用KF预测目标在当前帧的位置,将预测值作为初值,用MS算法搜索目标的位置。然后将搜索结果作为KF的观测值修正预测值,从而得到一个更精确的状态向量的后验估计。RAKF算法能够根据目标模型与候选目标模型及相应背景模型的Bhattacharyya系数自适应调整KF算法的参数。
为了降低跟踪算法的时间复杂度,将目标中心的x坐标和y坐标分开考虑,采用2个RAKF分别对应于目标中心的x坐标和y坐标,从而将2-D跟踪降为2个1-D跟踪。
2.1 卡尔曼滤波模型
KF通过递归的方式估计动态系统的状态。KF的系统方程为:
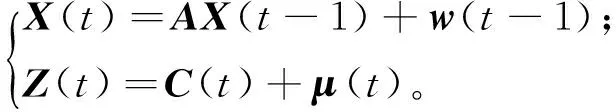
(5)
式中:X(t)表示t时刻的状态向量;A为状态转移矩阵;w(t-1)为激励噪声;Z(t)为观察向量;C为观测矩阵;μ(t)为观察噪声。w(t-1)和μ(t)为相互独立的高斯白噪声。w(t-1)和μ(t)的均值为零,协方差矩阵分别为Q(t-1)和R(t)。
定义X=(x,v,a)T,Z=x,其中x、v和a分布表示目标(水平或垂直方向)的中心、速度和加速度。在实际应用中,由于目标的运动模型通常不断变化,很难得到一个精确的系统状态方程。然而在一个较短的时间内,通常目标以某种近似恒定的规律运动,可认为是一个时不变系统。故定义式(5)中的状态转移矩阵为
(6)
其中:Δt为时间间隔。式(5)中的观测矩阵
C=(1,1,0)。
(7)
激励噪声的协方差矩阵定义为

(8)
观测噪声的协方差R(t)定义为
(9)
2.2 参数选择
在KF算法中,状态向量的后验估计为预测值和观测过程残余的加权线性组合[10]。当观测噪声的协方差趋于零时,观测过程残余的权重越来越大,此时,观测值对状态向量估计值的影响逐渐增加,而预测值对状态向量估计值的影响逐渐减小;另一方面,当先验估计的协方差趋于零时,观察过程残余的权重越来越小,此时,观测值对状态向量估计值的影响逐渐减小,而预测值对状态向量估计值的影响逐渐增加。因此,如果能够知道激励噪声和观测噪声的协方差,就可以使KF算法达到接近最优的性能。
MS目标跟踪算法通常选择目标区域为一个包含目标的椭圆区域。本文将介于矩形与椭圆之间的区域称为背景区域。矩形与椭圆的中心相同,长和宽分别平行于椭圆的长轴和短轴,长度是它们的1.5倍。目标模型与候选目标区域周围背景区域的背景模型之间的相似性度量了背景对跟踪的干扰程度。当目标模型与候选目标模型的匹配越好,且与相应背景模型的差异越大,背景对跟踪的干扰也就越小,跟踪结果的可靠性越高。
在AKF算法中选择参数时只考虑了目标模型与候选目标模型的相似性,没有考虑背景对跟踪的影响。当目标周围含有与目标相似的特征时,即使目标模型与候选目标模型的Bhattacharyya系数较大,MS算法的跟踪结果是不可靠的。在这种情况下,如果只根据目标模型与候选目标模型的Bhattacharyya系数调整KF算法的参数易引起目标的丢失和定位偏差。为了克服以上不足,RAKF算法在选择参数Q(t-1)和R(t)时,不仅考虑了目标模型与候选目标模型的相似性,同时还考虑了目标模型与候选目标区域周围背景区域的背景模型的相似性,从而提高了AKF跟踪算法对遮挡的鲁棒性。
记以y为中心候选目标区域周围背景区域的背景模型为
(10)
式中:nb为背景区域像素个数,{xi}i=1,…,nb为以y为中心候选目标区域周围的背景区域像素坐标集。目标模型与背景模型的Bhattacharyya系数为
(11)


(12)

(13)
其中:
(14)
(15)
若选择T=1,且α=0,则RAKF算法退化为AKF算法。因此,AKF算法是RAKF算法的一种特殊情况。

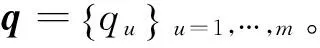
(1)分别用KF算法预测t+1帧目标的水平位置和垂直位置;

(4)计算Q(t)和R(t+1);

3 实验结果
为了验证本文算法的有效性,在Matlab环境下,选取多个视频序列进行测试,并将跟踪结果分别与MS和AKF算法的跟踪结果进行比较。颜色空间为RGB空间,并将其量化为16×16×16个区间,核函数为Epanechnikov核函数。目标的初始位置通过手动选择。在AKF和RAKF算法中,通过实验选择参数T=1 000,λ=0.15和α=0.35。
图1为测试序列一的第20、40、64、72和93帧跟踪结果。该序列共100帧,每帧大小为640×320像素。参数T0=0.83,T=0.35。在第一帧通过手动选择33×43的椭圆区域作为目标区域。核函数带宽h为[16,21]。由图1可知,当目标没有被遮挡时,MS算法、AKF算法和RAKF算法都能有效地跟踪目标。当目标被遮挡时,MS算法无法有效跟踪目标。而AKF算法和RAKF算法都能有效地跟踪目标。
图2为测试序列二的第20、48、75和84帧跟踪结果。该序列共90帧,每帧大小为640×320像素。参数T0=0.83,T=0.39。在第一帧通过手动选择29×39的椭圆区域作为目标区域。MS算法中核函数带宽h为[14,19]。由图2可知,当目标没有被遮挡时,MS算法、AKF算法和RAKF算法都能有效地跟踪目标。在第75帧,当目标被遮挡时,MS算法开始跟踪到错误的目标。由于目标被具有与目标相似颜色特征的人脸遮挡,所以目标模型与候选目标模型的Bhattacharyya系数仍然较大,导致AKF算法开始跟踪到错误的目标。而RAKF算法在调整KF的参数时,考虑了目标周围的背景区域,所有RAKF算法能有效地跟踪目标。

图1 测试序列一的第20、40、64、72和93帧跟踪结果

图2 测试序列二的第20、48、75和84帧跟踪结果
4 结 论
MS目标跟踪算法简单快捷,实时性好,获得了广泛的应用。但是当目标运动速度较快或者目标被遮挡时无法有效跟踪目标。KF是一种高效率的递归滤波器,它通过递归的方式估计动态系统的状态。为了进一步提高MS目标跟踪算法的鲁棒性,本文提出了一种基于MS的RAKF目标跟踪算法。RAKF算法能够根据目标模型与由均值漂移算法搜索得到的候选目标模型及相应背景模型的Bhattacharyya系数自适应地调整KF算法的参数,从而对遮挡具有较强的鲁棒性。
[1] Comaniciu D,Meer P,Mean shift.A robust approach to feature space analysis[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(5):603-619.
[2] Comaniciu D,Ramesh V,Meer P.Kernel-based object tracking[J].IEEE Trans Pattern Anal Mach Intell,2003,25(5):564-577.
[3] Li F W,Yan H Y.Forward-backward mean-shift for visual tracking with local-background-weighted histogram[J].IEEE Transactions on Intelligent Transportation Systems,2013,14(3):1480-1489.
[4] Yu W S,Tian X H.Multi-scale mean shift tracking[J].IET Computer Vision,2015,9(1):110-123.
[5] Comaniciu D,Ramesh V.Mean shift and optimal prediction for efficient object tracking[C].Proc IEEE Intl Conf Image Process,2000:70-73.
[6] Lee W,Chun J,Choi B I,et al.Hybrid realtime tracking of non-rigid objects under occlusions[C].Proc SPIE 2009,7252,72520F.
[7] Ren J,Hao J.Mean shift tracking algorithm combined with Kalman filter[C].2012 5th International Congress on Image and Signal Processing,2012:727-730.
[8] Babu R V,Perez P,Bouthemy P.Robust tracking with motion estimation and local kernel-based color modeling[J].Image and Vision Computing,2007,25(8):1205-1216.
[9] Li Xiaohe,Zhang Taiyi.Object tracking using an adaptive Kalman filter combined with mean shift[J].Optical Engineering,2010,49(2):020503.
[10] Welch G,Bishop G.An introduction to the Kalman filter[C].Proc ACM SIGGRAPH Conf,Los Angeles,CA,Aug,2001.
责任编辑:张新宝
2015-01-14
国家自然科学基金(编号:51174162);陕西省教育厅专项科研计划(编号:14JK1584);西安市科技计划(编号:CXY1346(7));西安石油大学青年科技创新基金(编号:2013BS021)
李小和(1974-),男,博士,讲师,主要从事图像处理与模式识别研究。E-mail:lixhxsyu@gmail.com
1673-064X(2015)05-0106-05
TP391.4
A

