考虑吸附、滑脱和自由分子流动效应的页岩基质渗透率计算模型
曹 成,李天太,刘 刚,高 潮,王 宇
(1.中国石油大学(北京) 石油工程学院,北京 102249;2.陕西延长石油(集团)有限责任公司 研究院,陕西 西安 710075;3.西安石油大学 石油工程学院,陕西 西安 710065)
考虑吸附、滑脱和自由分子流动效应的页岩基质渗透率计算模型
曹 成1,2,李天太1,3,刘 刚2,高 潮2,王 宇2
(1.中国石油大学(北京) 石油工程学院,北京 102249;2.陕西延长石油(集团)有限责任公司 研究院,陕西 西安 710075;3.西安石油大学 石油工程学院,陕西 西安 710065)
为了研究页岩吸附层在不同含水饱和度和压力下对基质渗透率的影响,采用毛细管模型,并结合现有表观渗透率计算模型,分别建立考虑吸附、滑脱和自由分子流动效应的有机质渗透率、无机质渗透率和综合渗透率计算模型;通过与实验结果、现有渗透率计算模型结果对比,该模型在计算具有吸附特性的页岩气藏基质渗透率时与实验结果更接近,更符合实际情况。以鄂尔多斯盆地上古生界山西组页岩为例,探讨页岩基质渗透率变化特征,结果表明:①对于孔径小于10nm的有机质孔,在开发初期压力较高(30MPa)时,孔径越小,吸附气对有机质渗透率影响程度越大;在开发后期压力较低(5MPa)时,孔径越小,滑脱效应和自由分子流动效应对有机质渗透率增加程度越大。开发过程中,兰缪尔压力越大,有机质渗透率增大率越大。②无机质孔径越大,吸附水对无机质渗透率伤害越严重。
页岩气;有机质渗透率;无机质渗透率;综合渗透率;吸附层;滑脱效应;自由分子流动效应
近年来,页岩气作为常规油气类型的重要补充和接替,具有重要的战略地位。页岩气勘探开发正由北美向全球扩展[1]。页岩气藏因其资源丰富、潜力巨大成为研究的热点[2-3]。在国内,对页岩气的成藏机理、地质特征等方面的研究取得了一些进展。但由于页岩基质特有的微纳米尺度孔隙、强非均质孔隙结构和复杂多变的气体运移机制,使得对页岩气渗流规律的认识还停留在较初始的阶段。基质渗透率是气体渗流规律的重要体现,目前对于页岩基质渗透率的研究,大多基于达西渗透率,在此基础上考虑滑脱渗透率增量和克努森扩散(自由分子流动)渗透率增量[4],或者考虑应力敏感效应和基质收缩效应对达西渗透率的影响[5-6];Javadpour通过研究气体在纳米孔隙介质中的运移首次建立考虑气体滑脱和克努森扩散的表观渗透率数学模型[7],但忽略了吸附层厚度对渗透率的影响。吸附层在很大程度上减小气体在孔喉中的过流面积,会对页岩基质渗透率造成影响[8]。因此本文基于达西渗透率,建立考虑吸附气、吸附水、滑脱效应和自由分子流动效应的基质综合渗透率计算模型,以鄂尔多斯盆地上古生界山西组页岩为例,分析吸附、滑脱效应和自由分子流动效应对基质渗透率的影响。
1 基质渗透率影响因素
1.1 吸附层对基质渗透率的影响
微纳米级页岩基质孔隙壁面上的吸附层厚度与孔径属于同一数量级,吸附层的存在导致气体在孔隙通道中的过流面积减小,因此对基质的渗透率造成影响。对于有机质孔隙系统,孔隙壁面的吸附层主要为甲烷气体[9],且吸附气层的厚度随着孔隙压力而变化,因此吸附气层对有机质渗透率[10]的影响是随着压力而变化的。对于无机质孔隙系统,孔隙壁面的吸附层主要为水层[9],由于无机质孔隙系统为水润湿性,在开发过程中毛管力的作用很强,裂缝中的水会被吸入无机质孔隙中,使得无机质孔隙含水饱和度增加,因此吸附水层对无机质渗透率[10]的影响是随着含水饱和度而变化的。
1.2 滑脱效应和自由分子流动效应对基质渗透率的影响
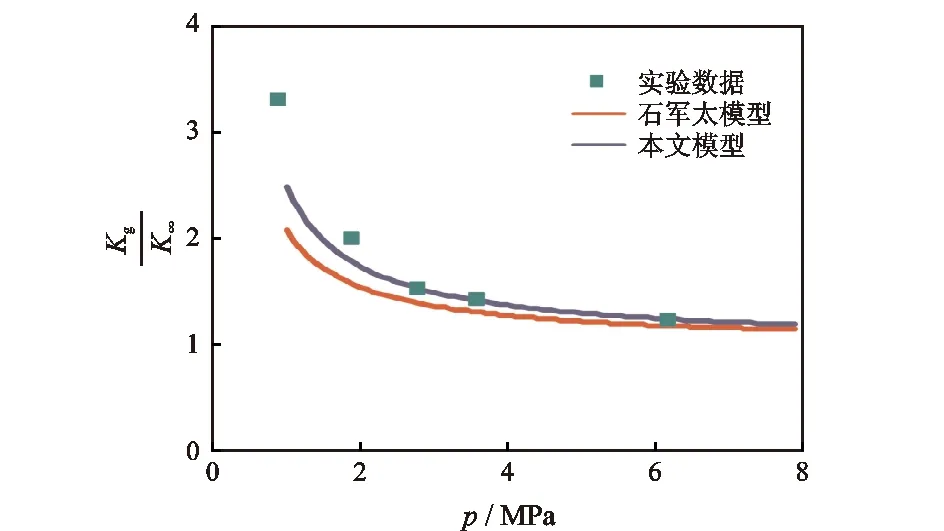
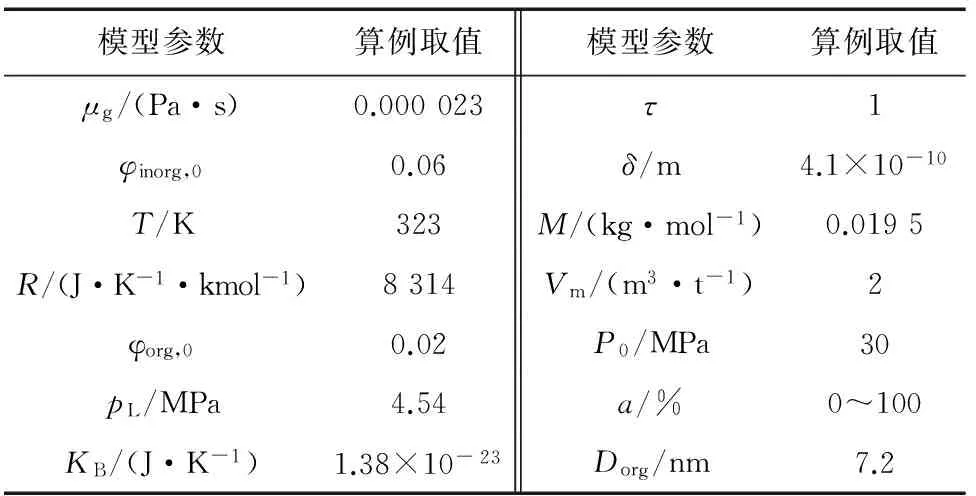
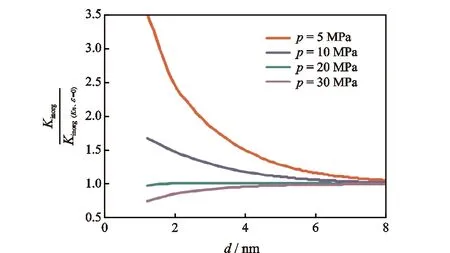
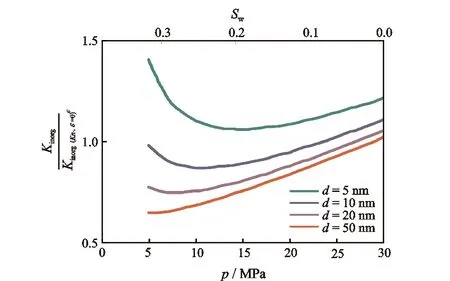
滑脱效应和自由分子流动效应是孔隙内气体分子与孔壁碰撞的宏观表现,当气体分子平均自由程与页岩基质孔径接近时,气体分子与孔壁的碰撞概率增大,产生滑脱效应;当气体分子平均自由程远大于孔隙通道时,气体分子与孔壁发生强烈碰撞,产生自由分子流动效应[10];滑脱效应和自由分子流动效应使气体更容易通过孔道,从而对基质渗透率产生影响。克努森数[10]Kn可用来判断滑脱效应和自由分子流动效应对基质渗透率的影响程度。当Kn<0.001时,不存在滑脱效应和自由分子流动效应的影响,当0.001 流动效应共同影响;当Kn>10时,只存在自由分子流动效应影响。据前人研究,对于微纳米尺度页岩基质孔隙[11],存在滑脱效应和自由分子流动效应共同影响页岩基质渗透率[12-14],滑脱效应和自由分子流动效应对基质渗透率的影响可通过表观渗透率模型[10]表征,即 (1) 式中:kap为表观渗透率,10-3μm2;φ为孔隙度;D为孔径,m;τ为迂曲度;Kn为克努森数;μg为气体黏度,Pa·s;δ为分子碰撞直径,m;KB为玻尔兹曼气体常数1.38×10-23, J/K;R为气体常数8 314, J·K-1·kmol-1;M为气体摩尔质量,kg/mol;T为绝对温度,K。 模型假设及参数:假设页岩单元体由n根圆柱形有机质纳米孔道与m根圆柱形无机质纳米孔道组成,单元体长度为L,单元体横截面积为A,a为横截面上有机质含量(面积百分比)。对于有机质孔:孔隙直径为Dorg,初始压力条件下的有效孔隙直径为Dorg,0,压力降低到p时的有效孔隙直径为Dorg,p(图1(a));对于无机质孔:初始有效孔隙直径为Dinorg,0,含水饱和度为Sw条件下的有效孔隙直径为Dinorg(图1(b))。有机质与无机质的润湿性和孔径差别都较大,从而导致基质渗透率不能统一而论。本文对有机质和无机质分别建立渗透率计算模型,最后耦合为基质综合渗透率计算模型。 图1 纳米孔隙系统气体运移原理图 2.1 有机质渗透率计算模型 忽略有机质孔隙中的吸附水,气体在有机质孔隙壁面的吸附可用兰缪尔等温吸附方程[15]表示,即 (2) 式中:Vm为兰缪尔体积,m3/t;pL为兰缪尔压力,MPa;V为吸附体积,m3/t;p为压力,MPa。 初始压力p0条件下,单位质量岩石孔隙壁面上气体吸附体积V0可表示为 (3) 当压力降低到p时,单位质量岩石孔隙壁面上气体吸附量V可表示为 (4) (5) 有机质纳米管有效孔隙度 (6) (7) (8) 得到考虑吸附气、滑脱效应和自由分子流动效应的有机质渗透率计算模型 (9) 2.2 无机质渗透率计算模型 忽略无机质孔隙中的吸附气。有效孔隙直径为Dinorg所对应含水饱和度 (10) 化简为 (11) 考虑到孔隙度与孔径的关系,含水饱和度为Sw时的有效孔隙度与初始有效孔隙度比值 (12) 将式(11)与式(12)带入式(1),并令η为吸附水影响因子,即 (13) 得到考虑吸附水、滑脱效应和自由分子流动效应的无机质渗透率计算模型 (14) 2.3 综合渗透率计算模型 对于页岩基质,在压力差的作用下,气体分别通过有机质孔道和无机质孔道,气体总质量流量J由有机质孔道中的气体质量流量Jorg和无机质孔道中气体质量流量Jinorg两部分组成,即 J=Jorg+Jinorg, (15) 其中: (16) (17) 式中:ρ为气体密度,kg/m3;Δp为压力差,MPa。 将式(16)和式(17)带入式(15)得 (18) 定义基质综合渗透率 k=korga+kinorg(1-a), (19) 将式(9)与式(14)代入式(19),得到基质综合渗透率计算模型的表达式 (20) 采用文献[4]实验数据验证本文有机质渗透率计算模型。模型计算参数与实验岩心参数设为相同。计算结果与实验数据对比可看出(图2),石军太渗透率计算模型[10]未考虑吸附层厚度的影响,因此该模型计算得到的表观渗透率kg与绝对渗透率k∞比值低于实验值。但对于本文模型,在压力大于3 MPa条件下,计算结果与实验结果吻合程度较好,说明在均质毛细管条件下建立的有机质渗透率计算模型在压力大于3 MPa条件下对于强非均质页岩同样适用;但当压力低于3 MPa时,本文模型计算结果稍低于实验数据,这是由于本文模型在均质毛细管条件下建立,而实验所用岩心内的孔隙通道不均质,部分岩心孔道直径可能小于模型所给平均孔道直径,因此在压力较低时,显现更强的滑脱效应。对于实际气藏,地层压力一般都高于3 MPa,因此用本文有机质渗透率计算模型可有效预测实际开采中的气体渗透率。对于无机质渗透率计算模型,采用文献[17]实验数据验证,文献[17]中实验所用岩心的岩性、润湿性及孔隙大小均与本文无机质相似,自吸水实验渗透率变化与本文无机质吸水后渗透率变化趋势一致,可以验证无机质渗透率计算模型的可靠性。综合渗透率是有机质渗透率和无机质渗透率的线性组合,因此,在前两者验证的基础上综合渗透率计算模型自然可以得到验证。 图2 有机质渗透率计算模型的验证 鄂尔多斯盆地上古生界山西组页岩有机质含量丰富,有机质孔径大多小于10 nm,无机质孔径相对较大。虽然本区页岩孔径非均质性较强,但气藏压力较高,依据模型验证结果,应用本文模型可以准确预测该区渗透率。本次研究取山西组页岩有机质和无机质参数作为渗透率计算参数(表1),讨论基质渗透率的变化特征。 表1 页岩气藏参数 在不同压力和孔径下,吸附气、滑脱效应和自由分子流动效应对有机质渗透率的影响如图3,压力越高,考虑吸附气、滑脱和自由分子流动效应的有机质渗透率Korg与不考虑吸附气、滑脱和自由分子流动效应的有机质渗透率Korg(Kn、ε=0)的比值越低;压力为30MPa时,滑脱效应影响很小,吸附气厚度使气体流动截面减小,随着孔径的减小吸附气的影响增大,二者比值减小;当压力为20MPa时,滑脱效应增加使孔隙壁面气体流动加速,吸附气体解吸,孔道中的气体过流面积增大,在滑脱效应和解吸的共同作用下,二者比值随着孔径的减小降低程度减缓; 随着压力继续降低,自由分子流动效应开始产生影响,且气体流动面积也更大,二者比值随着孔径的降低而升高。因此,在开发初期(压力较高)阶段,吸附气对有机质渗透率影响较大,在开发后期滑脱和自由分子流动效应对有机质渗透率影响较大。 图3 吸附气、滑脱和自由分子流动效应对有机质渗透率的影响 兰缪尔压力是影响吸附气解吸的重要参数,以本区平均孔径7.2 nm为初始孔径,假定初始吸附分子层厚度均为0.7 nm[16],影响结果见图4。吸附层的存在使有机质渗透率降低,但随着压力的降低,气体解吸,吸附层厚度减小,有机质渗透率增加;不同兰缪尔压力显现出不同的解吸速度,兰缪尔压力越小,吸附气解吸量越小,有机质渗透率增速越慢。 图4 有机质渗透率动态变化特征 在开发过程中,基质孔隙压力降低的同时,无机质孔隙含水饱和度会相应增加。本文假设压力从30 MPa到5 MPa降低过程中,无机质孔隙中的含水饱和度从0增加到38%[17],实际应用时需采用无机质岩心吸水实验来确定含水饱和度的变化。从图5看,孔径越大,考虑吸附水、滑脱和自由分子流动效应的无机质渗透率与不考虑吸附水、滑脱和自由分子流动效应的无机质渗透率的比值越低;当孔径为50 nm时,气体滑脱效应影响很小,含水饱和度的增加使气体在孔隙中的流动截面减小,无机质渗透率随着含水饱和度增加而降低,二者比值减小;随着孔径的减小,滑脱效应影响增强,无机质渗透率随着含水饱和度增加有上翘趋势;当孔径小于10 nm时,滑脱和自由分子流动效应同时作用,随着含水饱和度增加,无机质渗透率先降低后升高。 图5 吸附水、滑脱和自由分子流动效应对无机质渗透率的影响 取有机质孔径为10 nm、无机质孔径为50 nm,不同有机质含量下综合渗透率与孔隙压力之间的关系见图6。可以看出,当有机质含量为100%时,综合渗透率由有机质渗透率决定。初始阶段,考虑吸附气的综合渗透率与不考虑吸附气的综合渗透率比值aKorg/Korg(Kn、ε=0)+(1-a)Kinorg/Kinorg(Kn、η=0)低于1,但随着压力的降低,解吸与滑脱效应的综合作用使二者比值增大,综合渗透率升高;当有机质含量为80%时,初始阶段,较大的无机质孔隙使综合渗透率高于有机质含量为100%时的综合渗透率,但无机质含水饱和度持续增加使综合渗透率相对于有机质含量为100%时降低;当有机质含量为0%时,综合渗透率即为无机质渗透率,开发降压过程中,无机质孔隙的自吸水作用使综合渗透率持续降低。可以看出,无机质含量越多,开发初期综合渗透率越高,但到开发后期,含水饱和度的增加很大程度上会降低综合渗透率。对于实际页岩气藏,页岩有机质含量高低不一,且有机质渗透率和无机质渗透率差别较大,使用综合渗透率计算模型可有效避免有机质渗透率和无机质渗透率的差异所造成的计算偏差。 图6 吸附气、吸附水、滑脱和自由分子流动效应对综合渗透率的影响 (1)采用毛细管模型建立考虑吸附气、吸附水、滑脱和自由分子流动效应的基质综合渗透率计算模型。经验证,该模型更全面地考虑了吸附层厚度对基质渗透率的影响,并区分计算页岩中的有机质和无机质渗透率,修正吸附影响所造成的计算误差,有效避免有机质渗透率和无机质渗透率的差异性所造成的计算偏差。 (2)吸附气对有机质渗透率的影响是不可忽视的。在开发初始阶段,吸附气对有机质渗透率的影响最显著,且孔径越小,影响越大;随着压力的降低,吸附气影响逐渐减小,但滑脱效应逐渐增强,到开发后期,孔径越小,滑脱效应和自由分子流动效应的影响越大。 (3)吸附水对无机质渗透率的影响主要表现在开发后期,且无机质孔径越大,吸附水对无机质渗透率的影响越大。 [1] 徐建永,武爱俊.页岩气发展现状及勘探前景[J].特种油气藏,2010,17(5):2-7. XU Jian-yong,WU Ai-jun.The development status of shale gas in the world and its exploration prospect in China[J].Special Oil and Gas Reservoirs,2010,17(5):2-7. [2] 姚军,孙海,樊冬艳,等.页岩气藏运移机制及数值模拟[J].中国石油大学学报:自然科学版,2013,37(1):91-98. YAO Jun,SUN Hai,FAN Dong-yan,et al.Transport mechanisms and numerical simulation of shale gas reservoirs[J].Journal of China University of Petroleum:Natural Science Edition,2013,37(1):91-98. [3] 张金川,金之钧,袁明生.页岩气成藏机理和分布[J].天然气工业,2004,24(7):15-18. ZHANG Jin-chuan,JIN Zhi-jun,YUAN Ming-sheng.Reservoiring mecahnism of shale gas and its distribution[J].Natural Gas Industry,2004,24(7):15-18. [4] 高树生,于兴河,刘华勋.滑脱效应对页岩气井产能影响的分析[J].天然气工业,2011,31(4):55-58. GAO Shu-sheng,YU Xing-he,LIU Hua-xun.Impact of slippage effect on shale gas well productivity[J].Natural Gas Industry,2011,31(4):55-58. [5] 李治平,李智峰.页岩气纳米级孔隙渗流动态特征[J].天然气工业,2012,32(4):50-53. LI Zhi-ping,LI Zhi-feng.Dynamic characteristics of shale gas flow in nanoscale pores[J].Natural Gas Industry,2012,32(4):50-53. [6] Palmer L,Mansoori J.How permeability depends on stress and pore pressure in coalbeds:a new model[C].SPE Annual Technical Conference and Exhibition.Denver,Colorado,USA:Society of Petroleum Engineers,1996. [7] Javadpour F.Nanopore and apparent permeability of gas flow in mud rocks(shale and siltstone)[J].Journal of Canadian Petroleum Technology,2009,48(8):16-21. [8] Sakhaee P A,Bryant S L.Gas permeability of shale[C].SPE Annual Technical Conference and Exhibition.Denver,Colorado,USA:Society of Petroleum Engineers,2011. [9] Passey Q R,Bohacsk K M,Esch W L,et al.From oil-prone source rock to gas-producing shale reservoir-geologic[C].SPE International Oil and Gas Conference and Exhibition.Beijing,China:Society of Petroleum Engineers,2010. [10] Shi J T,Zhang L,Li Y S,et al.Diffusion and flow mechanisms of shale gas through matrix pores and gas production forecasting[C].SPE Unconventional Resources Conference.Calgary,Alberta,Canada:Society of Petroleum Engineers,2013. [11] 田华,张水昌,柳少波,等.压汞法和气体吸附法研究富有机质页岩孔隙特征[J].石油学报,2012,33(3):419-427. TIAN Hua,ZHANG Shui-chang,LIU Shao-bo,et al.Determination of organic-rich shale features by mercury injection and gas adsorption methord[J].Acta Petrolei Sinica,2012,33(3):419-427. [12] Czvan F,Rai S C,Sonderceld H C,et al.Shale gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms[J].Transport in Porous Media,2010,86(3):925-944. [13] Li Y,Li X,Shi J,et al.A nano-pore scale gas flow model for shale gas reservoir[C].SPE Energy Resources Conference.Port,Spain,Trinidad:Society of Petroleum Engineers,2014. [14] Javadpour F,Fisher,Unsworth M,et al.Nanoscale gas flow in shale gas sediments[J].Journal of Canadian Petroleum Technology,2007,46(10):55-61. [15] 程远方,董丙响,时贤,等.页岩气藏三孔双渗模型的渗流机理[J].天然气工业,2012,32(9):44-47. CHENG Yuan-fang,DONG Bing-xiang,SHI Xian,et al.Seepage mechanism of a triple-porosity/dual-permeability model for shale gas reservoirs[J].Natural Gas Industry,2012,32(9):44-47. [16] Ambrose R J,Hartman R C,Diza-Campos M,et al.New pore-scale considerations for shale gas in place calculations[C].SPE Unconventional Resources Conference.Pittsburgh,Pennsylvania,USA:Society of Petroleum Engineers,2010. [17] 齐银,张宁生,任晓娟,等.裂缝性储层岩石自吸水性实验研究[J].西安石油大学学报:自然科学版,2005,20(1):34-36,89-90. QI Yin,ZHANG Ning-sheng,REN Xiao-juan,et al.Experimental study on the hydroscopicity of fracture reservoir[J].Journal of Xi′an Shiyou University:Natural Science Edition,2005,20(1):34-36. 责任编辑:贺元旦 2015-03-20 国家高技术研究发展计划(863计划)“页岩气钻完井及储存评价与产能预测技术研究”(编号:2013AA064501);陕西省科技统筹创新工程计划“陆相页岩气资源地质研究与勘探开发关键技术攻关”(编号:2012KTZB03-01-01) 曹成(1984-),男,博士研究生,主要从事页岩气藏地质建模与数值模拟研究。E-mail:caochengyanlian@163.com 1673-064X(2015)05-0048-06 TE A
2 页岩基质渗透率计算模型


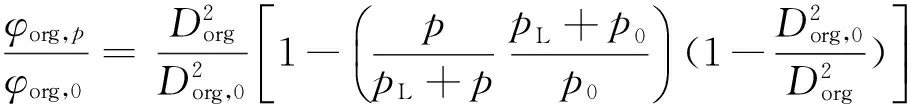
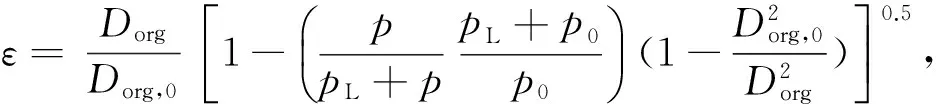
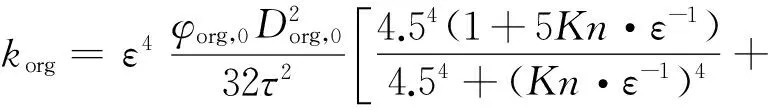


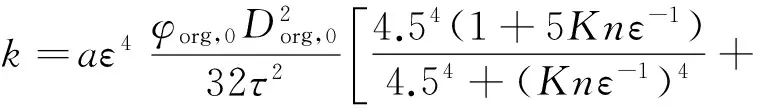
3 模型验证
4 实例计算


5 结 论
--先进无机材料论坛例记(Ⅰ)

