杠杆的动态平衡问题例析

张忠飞

杠杆的动态平衡问题，因题目条件的各种不同表述，显得极为繁杂。但其实，只要抓住杠杆平衡问题的关键——杠杆的平衡条件F1l1=F2l2作为判断依据，便可分析杠杆平衡条件中的力、力臂的变化类型及变化趋势，使杠杆动态平衡问题迎刃而解。本文将列举几组典型例题，将之分为再平衡和不再平衡两类，以杠杆的平衡条件F1l1=F2l2作为根本方法，对例题进行一一解析，帮助同学们突破杠杆动态平衡的难点。

一、再平衡问题

1.单一力不变

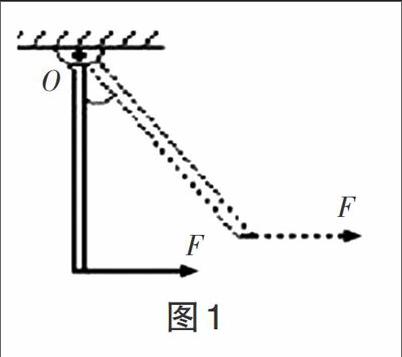
【例题】 如图1，重为G的均匀木棒竖直悬于O点，在其下端施一水平拉力F，让木棒缓慢转到图中虚线所示位置。在转动的过程中（ ）。

A. 动力臂逐渐变大

B. 阻力臂逐渐变小

C. 动力F逐渐变大

D. 动力F逐渐变小

解析：杠杆在转动过程中，一直保持平衡状态，从图2可以看出，F2（G）不变，l2变大，l1变小，根据杠杆平衡条件F1l1=F2l2，则F1（F）变大。故答案为C。

小结：从题目条件中找出，杠杆再次平衡时，平衡条件中的不变量为阻力G；变量阻力臂l2变大，动力臂l1变小，从而可知动力F的变化趋势。

【变式】如图3所示，轻质杠杆一端因受始终在水平方向上的力F作用而被逐步抬起，在此过程中F及力臂的大小变化分别是（ ）。

A. 变大、变大 B. 变大、变小

C. 变小、变大 D. 变小、变小

解析：杠杆抬起至水平的过程中始终保持平衡状态，从图4可以看出，F2（G）不变，阻力臂l2变大，动力臂l1变小，由杠杆平衡条件，知F1（F）变大。故答案为B。

2.单一力、力臂不变

【例题】如图5所示，有一质量不计的长木板，左端可绕O点转动，在它的右端放一重为G的物块，并用一竖直向上的力F拉着，当物块向左匀速滑动时，木板始终在水平位置保持静止，在此过程中，拉力F（ ）。

A. 变小 B. 变大

C. 不变 D. 先变大后变小

解析：物块运动时，杠杆一直保持平衡状态，从图6可以看出，l1、F2（G）不变，l2变小，由杠杆平衡条件，得F1（F）变小。故答案为A。

【变式1】如图7所示，杠杆OA的B点挂着重物G，A端用细绳挂在圆弧EF上，此时OA恰成水平，且A点与圆弧形架EF的圆心重合。当绳AM的M端从E点缓慢滑到F点的过程中，绳对A点拉力的大小将（ ）。

A. 逐渐变大 B. 逐渐变小

C. 先变大再变小 D. 先变小再变大

解析：绳AM从E点滑到F点时，杠杆一直保持平衡状态，从图8可看出，l2、F2（G）不变，l1先变大后变小，由杠杆平衡条件F1l1=F2l2知，F1（F）先变小后变大。故答案为D。

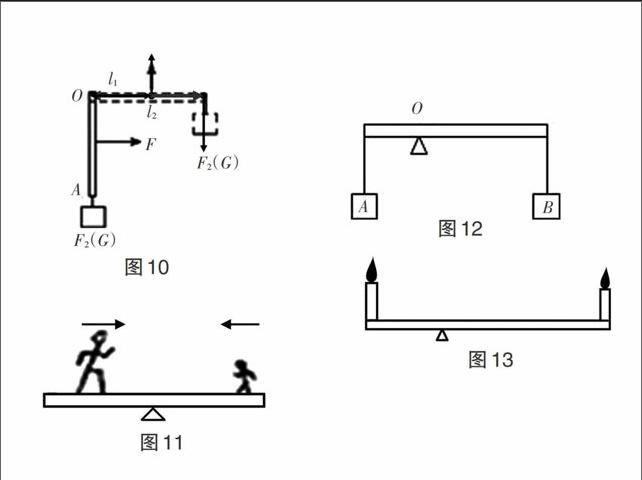
【变式2】如图9所示，直杆OA可O绕点转动，直杆下端挂一重物G。现用一个始终跟直杆垂直的力F将直杆由竖直位置缓慢转动到水平位置，在转动过程中这一直杆（ ）。

A. 始终是省力杠杆

B. 始终是费力杠杆

C. 先是费力杠杆，后是省力杠杆

D. 先是省力杠杆，后是费力杠杆

解析：杠杆从竖直位置缓慢转动到水平位置，始终保持平衡状态，从图10中可以看出，不变量为阻力F2（G）和动力臂l1，变量阻力臂l2变大，由杠杆平衡条件得F1l1=F2l2，从而可知动力F从0开始逐渐增大，当0≤FG时，为费力杠杆。故答案为D。

二、不再平衡问题

1. 力臂变化引起动态变化（动力、阻力不变，动力臂、阻力臂同时改变）

【例题】如图11所示，杠杆上分别站着大人和小孩（G大人>G小孩），且在水平位置平衡，杠杆自重不计，如果两人同时以大小相等的速度向支点移动，则杠杆将（ ）。

A. 不能平衡，小孩那端下沉

B. 不能平衡，大人那端下沉

C. 仍能平衡

D. 条件不够，无法判断

解析：方法1，设力臂均减小a，以杠杆平衡条件F1l1=F2l2作为判断依据，分析知，其中动力F1（G大人）、阻力F2（G小孩）不变，因为G大人>G小孩，即F1>F2，所以l1F2，所以F1a>F2a，故F1′l1′

方法2，用极端情况来分析，因为l1

故答案为A。

小结：以杠杆平衡条件作为杠杆平衡与否的判据，当符合“动力F1、阻力F2不变，动力臂l1、阻力臂l2同时改变”的题型时，必将要分析变化后F1l1′和F2l2′的大小，若F1l1′F2l2′，则杠杆向F1一端下沉。

【变式】如图12所示，杠杆处于平衡状态，如果将物体A和B同时向靠近支点的方向移动相同的距离，下列判断正确的是（ ）。

A. 杠杆仍能平衡

B. 杠杆不能平衡，左端下沉

C. 杠杆不能平衡，右端下沉

D. 无法判断

解析：此变式的条件与前一道例题其实是一样的，同学们自己用前面介绍的两种方法解解看。答案为C。

2.力的变化引起动态变化（动力臂l1、阻力臂l2不变，动力F1、阻力F2同时改变）。

【例题】如图13，若一根杠杆两端放有两截蜡烛，原来杠杆平衡，过一段时间后，两截蜡烛都燃烧掉一段，此时杠杆（ ）。

A. 仍保持平衡 B. 顺时针转动

C. 逆时针转动 D. 无法判断

解析：两截蜡烛燃烧了相同的时间，即两者质量减少相等，重力变化也相等。方法1，设重力均减小a，以杠杆平衡条件F1l1=F2l2作为判断依据。分析知，其中动力臂l1、阻力臂l2不变，且l1F1。因此变化后，F′1=F1-a，F2′=F2-a；F1′l1′=（F1-a）l1=F1l1-al1，F2′l2′=（F2-a）l2=F2l2-al2。因al1F2′l2′，即，杠杆向F1那端下沉，体现在图中，即为逆时针转动。

方法2，把时间延长至极端情况来分析，可知右侧蜡烛会先燃尽，此时F2l2=0，杠杆必定会向左侧蜡烛一端下沉。

故答案为C。

小结：以杠杆平衡条件作为杠杆平衡与否的判断依据，当符合“动力臂、阻力臂不变，动力、阻力同时改变”的题型时，必将要分析变化后F1′l1′与F2′l2′的大小。若F1′l1>F2′l2，则杠杆向F1一端下沉；若F1′l1

【变式1】如图14所示，每个钩码的重量都相等，杠杆处于平衡状态，若在杠杆两边的钩码下各再加一个相同的钩码，则杠杆（ ）。

A. 仍保持平衡

B. 向A端下降

C. 向B端下降

D. 因力臂长短不知，无法判断

解析：设力均增加a，以杠杆平衡条件[F1l1=F2l2]作为判断依据，分析知，其中动力臂[l1]、阻力臂[l2]不变。[F1>F2]，故[l1]<[l2]，而F1′l1′=F1′l1=（F1+a）l1=F1l1+al1，F2′l2′=F2′l2=（F2+a）l2=F2l2+al2，所以F1′l1′

【变式2】在轻质的杠杆两端AB各挂有体积相同的铜块和铝块（ρ铜>ρ铝）。支点O在如图15所示的位置时，杠杆在水平位置保持平衡，在下列情况下杠杆仍能在水平位置保持平衡的是（ ）。

A. 在铜块和铝块上各加一块质量相等的物体

B. 将铜块和铝块各切去体积相同的一小部分

C. 将铜块和铝块同时向支点移动一段相同的距离

D. 将铜块和铝块同时浸没在水中

解析：由前面的例题及变式，可以总结出一个规律：原来平衡的杠杆，在F1≠F2，l1≠l2的情况下，不管是以相等的量改变力还是力臂，杠杆均不能再保持平衡，具体证明同学可以用杠杆平衡条件[F1l1=F2l2]为依据自己推算。

故A、C、D项可先被排除。

B项，已知V铜=V铝=V0，由题意可知，F铜l铜=F铝l铝，即V0[ρ]铜l铜=V0[ρ]铝l铝，得出[ρ]铜l铜=[ρ]铝l铝。当铜块与铝快各切去体积相同的一部分V时，F′铜=（V0-V）[ρ]铜，F′铝=（V0-V）[ρ]铝，F′铜l铜=（V0-V）[ρ]铜l铜，F′铝l铝=（V0-V）[ρ]铝l铝，（V0-V）是相同的项，而[ρ]铜l铜=[ρ]铝l铝，故F′铜l铜=F′铝l铝，即杠杆仍保持平衡，故B是正确的。