CIR模型参数校准的极大似然法
赵芳芳,贾翔宇,许作良
(中国人民大学 信息学院,北京 100872)
【统计理论与方法】
CIR模型参数校准的极大似然法
赵芳芳,贾翔宇,许作良
(中国人民大学 信息学院,北京 100872)
针对CIR模型,利用Nowman方法得到近似转移密度函数,同时假设零息债券的市场价格与理论价格之间存在高斯误差,构造权重函数,应用加权极大似然方法对模型中的参数进行校准,并通过数值模拟验证了方法的有效性。
CIR模型;零息债券;加权极大似然方法
一、引 言
利率是自由金融市场中最基本也是最敏感的经济变量之一,几乎所有的金融现象和活动都和利率相关,而且其衍生产品交易非常活跃,如债券(包括零息和付息债券)、利率互换、债券期权等。随着利率市场化进程的不断推进,短期利率成为固定收益证券及利率衍生产品定价和企业风险管理不可缺少的工具,因此对短期利率随机行为进行研究的重要性日益突出。为刻画短期利率的随机行为,学者们在研究中引入随机微分方法,从利率期限结构的角度描述短期利率的动态过程。如何建立利率模型或有效刻画利率期限结构动态变化的特征,进而对利率的未来变化进行科学的预测,一直是当前金融领域研究的热点和难点。到目前为止,许多利率模型被提出并得到广泛应用。一般地,假设短期利率为r,利用下面的随机微分方程建立利率模型:
dr=μ(r,t)dt+σ(r,t)dZ(t)
(1)

不同的利率模型选取的漂移项或扩散项不同,其中被广泛应用的最简单利率模型是单因子模型。1973年Merton通过假设利率动态变化是一带有漂移项的布朗运动,最早提出了利率模型,即:
dr=μdt+σdZ(t)
(2)
其中μ,σ为常数。1977年Vasicek提出了以下具有均值回复特征的利率模型:
dr=a(θ-r)dt+σdZ(t)
(3)
其中a,θ,σ为常数,a是均值回复速率,θ是利率的长期均值水平[1]。1985年Cox等人对Vasicek模型进行了改进,克服了Vasicek模型中利率可能为负的理论缺陷,认为短期利率服从随机微分方程:
(4)
其约束条件为2aθ≤σ2,保证了利率一定非负,该模型简称为CIR模型[2]。CIR模型的一个重要特征是利率的波动率不再是常数,而是利率的增函数,即当利率上升时,其波动程度也随之加强。
至今,国内外学者已从多角度对利率进行了研究,并陆续提出了几十种描述利率期限结构动态变化的模型。研究者们不断地尝试或推广利率模型的主要动机是希望给出一个合适的模型,能够真实地刻画市场上的数据信息,从而能够更好地对其衍生产品定价和进行风险度量,这就导致了随机利率模型中参数校准问题的产生。所谓校准问题就是由一组已知数据来确定参数的值,通常将标的资产及其衍生产品的价格在一系列已知时刻的观测值作为已知数据。因此,利率模型中的参数校准问题是指由利率及其衍生产品市场价格的时间序列来确定参数的值。本文基于利率和零息债券的市场数据,考虑CIR模型中的参数校准问题。
随着参数校准问题的发展,很多有效并可行的校准方法应运而生,如正则化方法、极大似然法、最优化方法、核估计方法等[3-6]。众所周知,极大似然方法具有一致性、渐近正态性和渐近有效性的特点。考虑到方法的稳定性和有效性,极大似然法被广泛用来进行随机利率模型的参数估计,并取得了显著性的发展。2002年Durham等人以CIR模型为例比较了计算随机微分方程似然函数的多种数值方法,给出了偏差减小和方差缩减技术,另外还将估计方法扩展应用于随机波动率模型中[7]。2003年Hurn等人给出了随机微分方程参数估计的模拟极大似然方法,针对几何布朗运动模型和CIR模型,将结果与其它估计结果作比较,并通过用美国3个月财政数据对单因子利率期限结构模型做实证分析,证明了方法的有效性[8]。2009年Tang等人针对Vasicek模型和CIR模型,分别给出参数的极大似然估计量和由Nowman方法得到的伪极大似然估计量,由估计量的偏差及方差的展开式说明漂移项比扩散项的估计更为困难,并用Bootstrap过程进行了参数偏差修正[9]。基于极大似然方法,本文通过假设零息债券的市场价格与理论价格之间存在高斯误差,构造权重函数,利用加权极大似然方法讨论了CIR模型中参数的校准问题,从而使校准得到的模型不仅能更好地刻画利率的期限结构,更能准确地为其衍生产品进行定价。
二、利率与零息债券定价模型

(5)
其中a为均值回复速率,θ/a为利率的长期均值水平,2θ≥σ2,θ和σ2均为待估参数。
基于该模型,令η={θ,σ2},在时刻t,到期日为T,面值为1单位的零息债券价格P(t,r;η)为:
P=
(6)
(7)
终值条件为P(T,r;η)=1。基于文献[11]的结果,偏微分方程(7)存在一类仿射性结构解,即:
P(t,r;η)=exp(A(t)-rB(t))
(8)
将上式代入式(7),得到A(t),B(t)满足以下常微分方程:
A′(t)-θB(t)=0,A(T)=0
(9)
(10)
求解方程(9)和(10),得到:
(11)
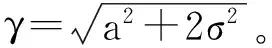
三、加权极大似然方法
利用极大似然方法进行参数校准时,关键在于求解模型的条件概率密度或转移密度函数。关于转移密度函数近似求解的方法有很多,如Euler法、SMLE法、Hermite法、Nowman方法等。尽管对于CIR模型,其真实的转移密度函数是已知的,但由于计算的复杂性,本文利用Nowman方法求解其近似转移密度函数[12]。
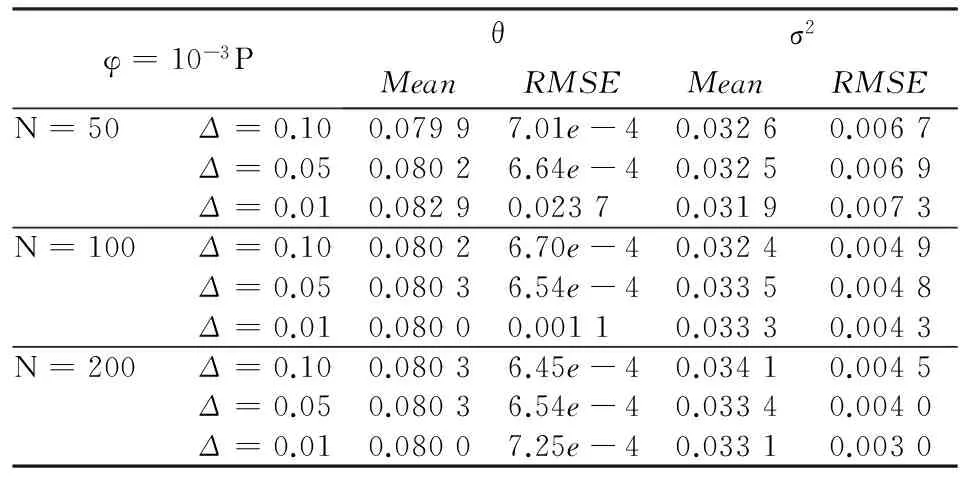
在时间点t0 (12) 其中εi满足条件: E(εi)=0E(εiεj)=0(i≠j) (13) f(ri+1|ri,η) (14) 由此可得到对数似然函数为: (15) 其中M={(θ,σ2)|2θ>σ2}。由于当观察次数足够多时,意味着lnf(r0,η)的权重很小,因此在实际的估计过程中,往往将上式中的第一项省略。求解L(η)的最大化,便可得到参数η的估计值。 Tang和Chen利用上述方法给出了CIR模型中参数的估计值及其渐进分析[9]。然而,此类方法局限于仅利用市场中的利率数据(如Euribor,Libor,Shibor)进行参数估计和实证分析,而实际市场中与利率密切相关的衍生产品的交易非常活跃,如债券、利率互换等,且其市场价格可以直接观测到,因此考虑将短期利率和零息债券市场价格的时间序列作为已知数据来校准CIR模型中的参数η。 (16) g(ri+1|ri,η) i=0,1,…,n-1 (17) 综合式(15)和式(17)得到CIR模型的加权对数似然函数为: 将式(8)代入上式,并省略常数项得到: 通过求解F(η)最大化,可以得到参数η的估计值,即: (18) 从F(η)的表达式可以看出,加入权重函数式(17)的目的是对于能够较好拟合零息债券市场价格的点,赋予权重大一些。相反,对于那些与零息债券的观测数据差距较大的点,则赋予的权重要小一些。 (19) 下面给出具体的数值计算方法。 不失一般性,本文取等距的离散时间点t0 对于Nowman方法,随着时间间隔不断减小,得到的转移概率密度近似值与真实的转移密度差距会越来越小,因此参数的校准值与真实值之间的差距也会越小;而对于极大似然方法来说,随着样本量的增加,参数校准值与真实值的差距也将越小。下面将分别从时间间隔、样本容量两个方面对数值结果进行分析。 表1 不同θ,σ2对应的数值结果 从表1中可以看出,当取φ=10-3P不变时,以上不同情况下对于θ和σ2两个参数的校准结果基本接近于其真实值。一方面,当样本容量N固定时,随着时间间隔Δ的不断减小,参数校准值越来越接近真实值,但当N较小时,其代价是根均值误差会增大,只有当样本容量达到200时,均方误差越来越小;另一方面,当时间间隔Δ不变时,随着样本容量的不断增加,参数校准值基本上越接近于真实值,且均方误差逐渐减小,因此比较而言当N=200,Δ=0.01时具有较好的数值结果。 另外,由于零息债券的市场数据通过表达式P=PM+u生成,其中u是服从均值为0,方差为φ的标准正态分布的随机数,因此为了考虑不同的噪声,表2表示的是当样本容量N固定,针对不同的Δ分别选取φ=10-2P,10-3P,10-4P三种情况下参数的校准结果。 从表2中可以看出,参数校准的数值结果基本是稳定的,但比较而言,当φ=10-3P时,具有更好的数值结果。 基于利率和零息债券价格的市场数据,本文给出了CIR模型中参数校准的极大似然方法。通过假设零息债券的市场价格与理论价格之间存在高斯误差,构造权重函数,从而得到加权对数似然函数,并通过数值模拟验证了方法的可行性。该方法使校准得到的利率模型不仅能够有效地刻画利率的期限结构,也能准确地为利率衍生产品进行定价,具有一定的实际意义。同时,该方法可以广泛应用于其他利率模型的参数校准。 [1]VasicekO.AnEquilibriurmCharacterizationoftheTermStructure[J].JournalofFinancialEconomics, 1977,5(2). [2]CoxJC,IngersollJE,RossSA.ATheoryoftheTermStructureofInterestRates[J].Econometrica, 1985,53(2). [3] 江良,徐承龙. 非高斯单因子短期利率模型正则化参数估计[J].计算物理,2012,29(6). [4] 江良,忻丁耀.基于正则化方法的Hull-White短期利率模型参数估计[J].同济大学学报:自然科学版,2012,40(10). [5] 杨柳,俞建宁,邓醉茶,等. 一个关于零息票定价的反问题[J].四川大学学报:自然科学版,2007,44(6). [6] 张玉贵,苏云鹏,杨宝臣.基于Vasicek和CIR模型的SHIBOR期限结构实证分析[J].统计与信息论坛,2009,24(6). [7]DurhamGB,GallantAR.NumericalTechniquesforMaximumLikelihoodEstimationofContinuousTimeDiffusionProcesses[J].JournalofBusinessandEconomicStatistics,2002,20(3). [8]HurnAS,LindsayKA,MartinVL.OntheEfficacyofSimulatedMaximumLikelihoodforEstimatingtheParametersofStochasticDifferentialEquations[J].JournalofTimeSeriesAnalysis, 2003, 24(1). [9]TangCY,ChenSX.ParametersEstimationandBiasCorrectionforDiffusionProcesses[J].JournalofEconometrics, 2009,149(1). [10]HullJ,WhiteA.PricingInterestRateDerivativeSecurities[J].TheReviewofFinancialStudies, 1990,3(4). [11]DuffieD,KanR.AYield-FactorModelofInterestRates[J].MathematicalFinance, 1996,6(4). [12]NowmanKB.GaussianEstimationofSingleFactorContinuousTimeModelsoftheTermStructureofInterestRates[J].JournalofFinance, 1997,52(4). (责任编辑:崔国平) A Maximum Likelihood Method for Calibrating the Parameters of CIR Model ZHAO Fang-fang,JIA Xiang-yu,XU Zuo-liang (School of Information, Renmin University of China, Beijing 100872, China) For CIR model, we obtain approximate transition density function by using Nowman's method and construct weight function by supposing there exists a Gaussian error between the theoretical and market prices of zero-coupon bonds.Then applying the weighted maximum likelihood method, we calibrate the parameters of the model.Finally, numerical simulations are carried out to confirm effectiveness of the method. CIR model;zero-coupon bond;weighted maximum likelihood method 2015-04-24 国家自然科学基金项目《金融中的反问题及数值计算》(11171349) 赵芳芳,女,山东新泰人,博士生,研究方向:反问题与金融计算; 贾翔宇,男,河北唐山人,博士生,研究方向:反问题与金融计算; 许作良,男,辽宁新金人,理学博士,教授,博士生导师,研究方向:反问题及其应用,金融计算。 O242.1∶F830.91 A 1007-3116(2015)09-0003-05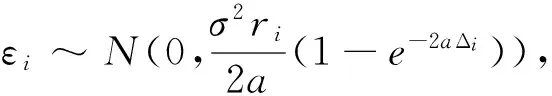
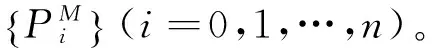
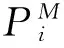
四、数值实验
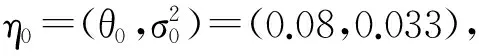
五、结 论

