基于均匀正交设计的消力池内双层悬栅布置优化试验
蒋健楠,牧振伟,张佳祎,贾萍阳
(新疆农业大学 水利与土木工程学院,新疆 乌鲁木齐 830052)
基于均匀正交设计的消力池内双层悬栅布置优化试验
蒋健楠,牧振伟,张佳祎,贾萍阳
(新疆农业大学 水利与土木工程学院,新疆 乌鲁木齐 830052)
由于在消力池内布置双层悬栅对消能效果影响少有研究,考虑到单宽流量、悬栅栅条数、栅距和层距等影响因素,采用均匀正交设计,考察4因素3水平,选择UL9(34)优化方案进行模型试验,对比了不同流量和悬栅布置型式组合下消力池内下降水深及消能率。试验结果表明:不考虑单宽流量时,消力池内布置双层悬栅,下降水深受层距、栅条数以及栅距影响较大,其中层距改变影响最大,消能率受这些影响因素影响较小;单宽流量较小时,层距和栅距均与下降水深成正比关系,单宽流量较大时,层距与下降水深成正比关系。
双层悬栅;均匀正交设计;下降水深;层距;栅距;栅条数
1 研究背景
在底流消力池内增设辅助消能工是提高消力池消能效果常用的方式,但新疆大多数河流含沙量较大,底孔出流的消力池不仅要起到消能作用,还要兼顾排沙,一些常见的辅助消能工均设置在消力池底板上,极易受到含沙水流的冲刷,影响消能效果。悬栅消能工是新疆农业大学水工实验室发明的一种新型辅助消能工,因其悬挂在消力池内,不易受到含沙水流冲刷,能有效地起到辅助消能作用。悬栅消能工现已成功应用在新疆五一水库、小石峡等工程中。已有人结合这些工程,采用模型试验和数值模拟等方法,对悬栅进行了研究,侯杰等[1]通过陡坡悬栅模型试验,得到了陡坡悬栅的水力特性;张建民等[2]利用多普勒激光测速系统测试了悬栅和悬栅板附近流场,对悬栅和悬栅板流场进行了分析;吴战营等[3-4]对消力池内悬栅辅助消能工进行了优化试验,确定了新疆迪那河五一水库溢洪洞消力池悬栅消能工的最佳方案;朱玲玲[5]采用PPR投影寻踪回归分析方法和流体力学软件FLUENT数值模拟手段,进行了底流消力池内悬栅消能工布置型式对消能效果影响研究,得出了消力池内消能效果影响因子排序。但此前研究大都针对单层悬栅,而双层悬栅布置情况却少有研究。前期试验表明,消力池内布置双层悬栅较单层悬栅消能效果更优,有必要深入研究双层悬栅对消力池消能效果的影响规律。消能效果影响因素包括流量、层距、栅距、栅条数等,考虑到消能效果影响因素较多,运用均匀正交设计[6-10]理论对消力池内布置双层悬栅试验进行优化设计。本文通过优化后的模型试验,探究双层悬栅各影响因素对消能效果影响规律。
2 试验设计
2.1 模型设计为研究消力池内布置双层悬栅后对消能效果的影响,采用q0=21.43 L/s为试验单宽流量设计值,通过相关水力计算[11]得到消力池尺寸,其中消力池长120 cm、宽18 cm、深10 cm、边墙高39.5 cm。悬栅采用矩形悬栅,悬栅栅条长18 cm、宽1 cm、高2 cm,悬栅呈“W”型布设,消力池结构及悬栅布置见图1。为了便于观测,试验模型制作均采用有机玻璃板,试验模型总体长约9.3 m,分别由供水水箱、进口引水段、消力池、出口泄水段以及三角形量水堰组成。

图1 消力池结构及悬栅布置(单位:cm)
2.2 试验优化设计布置悬栅时,在消力池渥奇段布置4根悬栅,取栅高(悬栅中心点距消力池底板高度)h=7 cm、栅距(相邻两根悬栅水平之间的距离)b1=3.5 cm。为使水流更好地进入消力池,在消力池前端布置1根悬栅,取栅高h=8.5 cm,与渥奇段悬栅之间栅距b1=3.5 cm。改变消力池内悬栅布置型式时,为便于试验研究,保持渥奇段4根和消力池前端1根悬栅位置不变,只改变消力池内悬栅栅距b1、栅条数n、间距b2以及单宽流量q0。
2.3 试验手段最大水深采用测针测量,精度为0.1mm,取断面水位最高处读数与该断面底部读数之差为最大水深H;流量的测量调节采用三角形量水堰;消力池内流态采用肉眼观察方式,并用高清摄像机拍照记录。
消能率计算为:

其中:

式中:h1、h2分别为来流、出流断面水深,cm;v1、v2分别为来流、出流断面流速,cm/s;E1、E2分别为来流、出流断面的能量;ΔE为消力池消耗的能量;a为来流、出流断面高程差,取a=13.8 cm。
2.4 试验结果
2.4.1 单、双层悬栅消能效果对比 通过在消力池内布置单层和双层悬栅,在单宽流量q0=21.43 L/s下进行试验得到消力池内流态图(见图2)和单、双层悬栅消能效果对比(见表1)。
图2(a)是在消力池内布置双层悬栅,其中栅距b1=12 cm、栅条数n=11根、层距(即上层栅高与下层栅高之差,简称:层距)b2=4 cm;图2(b)是布置单层悬栅,其中栅距b1=5.5 cm、栅条数n=11根。从图2可知,布置双层悬栅,水跃主要集中在渥奇段和消力池前段,消力池后段水流平稳,没有剧烈波动,消能效果较好;布置单层悬栅,水跃后移至消力池中后段,消力池内水流波动较大,消能效果不理想。

图2 消力池内流态
表1给出了消力池内布置单层和双层悬栅后消力池内最大水深、下降水深(即消力池内布置双层悬栅后最大水深相对未布置悬栅时最大水深下降的水深)及水跃型式。由表1可知,相同流量下,栅条数相同或者栅条数较少时,布置双层悬栅,消力池内流态更加平稳,水面波动较小,较布置单层悬栅方案更优;消力池内布置悬栅后,在消力池内流态均稳定和栅条数一定时,布置双层悬栅,消力池内最大水深下降更多。2.4.2 双层悬栅优化方案设计 在不同单宽流量下,首先对消力池内未布置悬栅进行模型试验,观察消力池内流态,测量消力池内最大水深并计算消能率,然后对消力池布置双层悬栅进行模型试验,观察布置双层悬栅对消力池消能效果的影响,并测量消力池内最大水深,计算下降水深以及消能率,下降水深为布置悬栅前后消力池内最大水深下削减的水深。
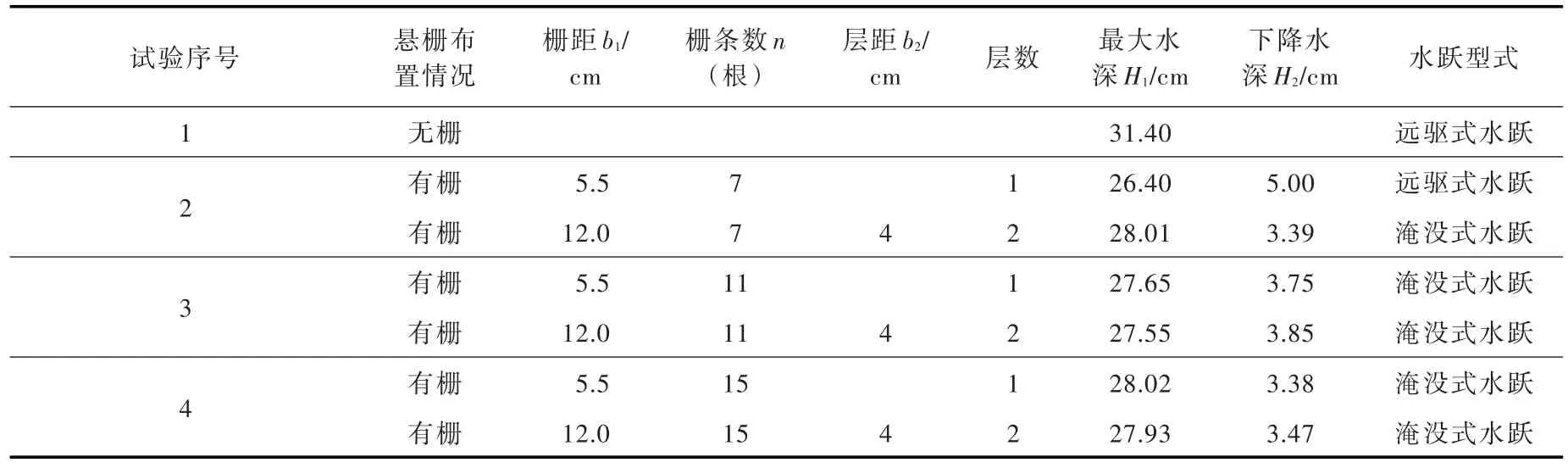
表1 单、双悬栅消能效果对比
研究每个因素对消能效果的影响需要大量试验,为此需对试验进行优化设计。在设计试验时,需要考察4因素3水平,采用均匀正交表不但具有正交性还具有均匀性,比标准正交表更能减少重复,减少多水平多因素试验次数。考虑多方面因素,选择UL9(34)进行试验方案优化设计,其中栅条数n取7根、11根、15根,栅距b1取8、10、12 cm,层距b2取2、3、4 cm,单宽流量q0取15.71、18.57、21.43 L/s,得到优化试验方案见表2。

表2 均匀正交试验优化方案
3 消能效果影响因素排序
通过试验得到未布置悬栅时消力池内流态、最大水深以及消能率(表3)和悬栅不同布置型式下消力池内最大水深、下降水深和消能率(见表4)。由表3、表4可知,消力池内布置悬栅后,水流均在消力池内形成淹没式水跃,水流流态相对稳定,消能率均有所提高,消力池内最大水深均有所下降;流量改变,对消力池内最大水深和消能率的影响比较大,消能率随着流量的增大而增大,说明在设计流量下,在消力池内布置双层悬栅能改善消力池消能效果。
在不考虑流量情况下,改变栅条数n、栅距b1及层距b2,对消力池消能效果同样有影响,消能率平均变化率为1.31%,下降水深平均变化率为38.23%,说明栅条数n、栅距b1及层距b2的改变,对消力池消能率影响较小,对下降水深影响较大。对4因素3水平所得的平均下降水深进行极差计算,可得栅条数n、栅距b1、层距b2对应平均下降水深的极差R1分别为0.40、0.73和0.75 cm,可知层距b2改变引起的平均下降水深极差最大,栅条数n改变引起的平均下降水深极差最小,各因素对平均下降水深的影响排序为层距b2、栅距b1、栅条数n。
试验表明,改变流量,水流速度和消力池内水深也同时改变,消力池内布置双层悬栅后,悬栅阻挡水流,将水流分成上、下两股,使上、下水流相互碰撞,增大水流掺气量,使水流中大部分能量耗散,流速和下降水深变化幅度也比较大;不考虑流量情况下,改变栅条数n和栅距b1,只改变了悬栅水平断面面积,垂直断面面积并未改变,水流与悬栅碰撞几率较小,水流掺气量较少,水跃减弱较慢,下降水深变化较小;改变层距b2,改变悬栅垂直断面面积,水流与悬栅碰撞几率增大,水流掺气量较多,水跃减弱较快,下降水深变化较大,说明改变悬栅层距对下降水深影响更大;流量不变,只改变悬栅栅条数n、栅距b1以及层距b2,水流经过悬栅掺气消能,流速减小,流量不变,水深增大,流速变化量和水深变化量相差不大,因此,消能率变化不大。

表3 未布置悬栅的试验结果
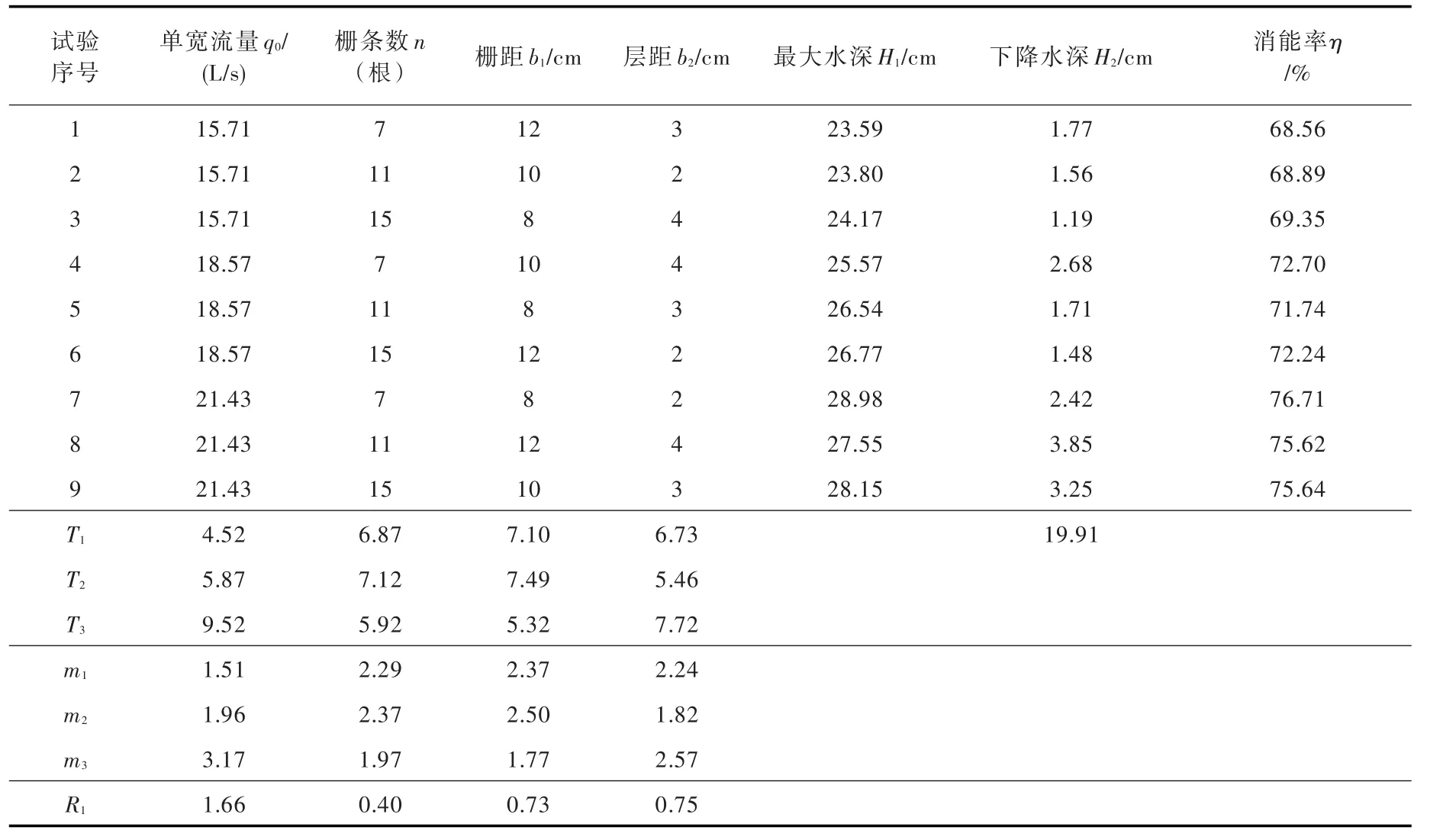
表4 布置悬栅后的试验结果
4 影响因素对下降水深影响规律
通过均匀正交试验发现,不同单宽流量q0下,改变栅条数n、栅距b1及层距b2布置型式对消力池下降水深影响也不一样。根据均匀正交试验,参考下降水深H2最大的1组悬栅布置型式,即栅条数n=11根、栅距b1=12 cm、层距b2=4 cm,分别改变栅条数n、栅距b1以及层距b2在q0=18.57 L/s和q0= 21.43 L/s下进行模型试验。
4.1 层距对最大水深影响规律保持栅条数n=11根和栅距b1=12 cm不变,改变层距b2,在q0=18.57 L/s和q0=21.43 L/s两种流量下进行模型试验,得到消力池下降水深见表5。由表5可见,下降水深随层距的增大而增大。试验表明,流量较小时,水流流速较小,携带的能量较小,流态紊乱程度较小,消力池内布置悬栅后,水流经过悬栅是掺气消能,使水流速度减小,只增大栅距层距b2,垂直断面面积增大,使水流与栅条碰撞更充分,消力池内最大水深下降逐渐增大,层距b2与下降水深成正比关系;单宽流量q0较大时,水流携带能量较大,流态紊乱程度较大,只增大层距b2,水流与栅条碰撞几率增大,消力池内水深下降随之增大,层距b2与下降水深H2成正比关系。

表5 悬栅布置不同层距时的下降水深

表6 悬栅布置不同栅距时下降水深
4.2 栅距对下降水深影响规律保持栅条数n=11根和层距b2=4 cm不变,改变栅距b1,在q0=18.57 L/s和q0=21.43 L/s两种流量下进行模型试验,得到消力池下降水深见表6。由表6可见,当单宽流量q0= 18.57 L/s时,下降水深随栅距增大而增大;当单宽流量q0=21.43 L/s时,随着栅距增大,下降水深先减小后增大。流量较小时,水流能量较小,紊乱程度较小,只增大栅距b1,水平断面面积增大,在一定程度上增大了水流与栅条碰撞几率,消力池内下降水深H2随之增大,此时栅距b1与下降水深成正比关系;单宽流量较大时,流态紊乱程度较大,只增大水平断面面积,水流与栅条碰撞增大的几率对水流影响较小,下降水深H2不随栅距b1增大而增大,此时,栅距b1与下降水深不成正比关系。
4.3 栅条数对下降水深影响规律保持栅距b1= 12 cm和层距b2=4 cm不变,改变栅条数n,在18.57 L/s和21.43 L/s两种流量下进行模型试验,得到消力池下降水深见表7。由表7可见,当q0= 18.57 L/s时,下降水深随栅条数增大而减小;当q0=21.43 L/s时,随着栅条数增大,下降水深先增大和减小。单宽流量较大或较小时,只改变栅条数n,悬栅水平断面和垂直断面面积均未增大,水流与栅条碰撞几率并未增大,水流掺气消去能量变化不大,且栅条数n增加,使水流过流能力减弱,水位雍高,下降水深H2较小,栅条数n与下降水深H2不成正比关系。
5 结论

表7 悬栅布置不同栅条数时下降水深
本文通过消力池内布置双层悬栅模型试验,对比试验结果得到以下结论:(1)在不考虑单宽流量情况下,在消力池内布置双层悬栅,改变悬栅栅条数、栅距以及层距,消能率的平均变化率为1.31%,对消能率影响较小;下降水深的平均变化率为38.23%,对下降水深影响较大;且各因素对下降水深的影响排序为层距、栅距、栅条数;(2)在单宽流量较小或较大时,层距与下降水深均成正比关系,栅条数与下降水深均不成正比关系;单宽流量较小时,栅距与下降水深成正比关系,单宽流量较大时,栅距与下降水深不成正比关系。
由于试验组数相对较少,本文只得出各影响因素与下降水深的大致变化趋势,至于其具体变化规律或其间函数关系仍需进一步探究。
[ 1] 侯杰,赵涛,牧振伟,等.悬栅消能工水力特性研究[J].水力发电,2004,30(1):36-39.
[ 2] 张建民,王玉蓉,杨永全,等.过悬栅、悬板栅水流流场测试及消能分析[J].四川大学学报:工程科学版,2002,34(2):36-38.
[ 3] 吴战营.消力池内辅助消能工试验研究及数值模拟[D].乌鲁木齐:新疆农业大学,2013.
[ 4] 吴战营,牧振伟.消力池内悬栅辅助消能工优化试验[J].水利水电科技进展,2014,34(1):27-31.
[ 5] 朱玲玲.底流消力池内悬栅消能工布置型式对消能效果影响研究[D].乌鲁木齐:新疆农业大学,2014.
[ 6] 方开泰,马长兴.正交与均匀实验设计[M].北京:科学出版社,2001.
[ 7] 夏之宁,谌其亭,穆小静,等.正交设计与均匀设计的初步比较[J].重庆大学学报:自然科学版,1999,22(5):112-117.
[ 8] 王宇平,焦永昌,张福顺 .解多目标优化试验的均匀正交遗传算法[J].系统工程学报,2003,18(6):481-486.
[ 9] 陶洪飞,邱秀云,赵丽娜,等.基于正交设计的分离鳃结构优化数值模拟研究[J].水力发电学报,2013,32(5):204-212.
[10] 谭义海,李琳,邱秀云 .梭锥管混浊流体分离装置水沙分离试验研究[J].新疆农业大学学报,2010,33(6):521-526.
[11] 邱秀云.水力学[M].乌鲁木齐:新疆电子出版社,2008.
Double suspended grid layoutoptimization test in the absorption basin based on the uniform orthogonal design
JIANG Jiannan,MU Zhenwei,ZHANG Jiayi,JIA Pingyang
(College of Water Conservancy and Civil Engineering,Xinjiang Agricultural University,Urumqi 830052,China)
Due to rare research on effect of energy dissipation of double suspended grid laying in absorp⁃tion basin,considering the discharge per unit width,suspended grid bar number,grid distance,layer dis⁃tance and other influencing factors,it adopts the uniform orthogonal design to investigate four factors three levels,choose UL9(34)optimization scheme for model test,and compares declined water depth and energy dissipation percentage in absorption basin under the combination of different flow and suspended grid ar⁃rangement type.Experimental results are shown that:(1) no considering about discharge per unit width,double suspended grid laid in absorption basin,declined water depth is greatly influenced by layer dis⁃tance,grid bar number and grid distance,where the influence of layer distance change is the greatest,but effect of energy dissipation is less influenced by these factors;(2)when the discharge per unit width is smaller,layer distance and the grid distance are proportional to declined water depth,while the dis⁃charge per unit width is bigger,the layer distance is proportional to the declined water depth.
double suspended grid;uniform orthogonal design;decline water depth;layer distance;grid distance;grid bar number
TV134
:Adoi:10.13244/j.cnki.jiwhr.2015.05.007
1672-3031(2015)05-0357-06
(责任编辑:王冰伟)
2015-03-31
国家自然科学基金项目(51469031);新疆优秀青年科技创新人才培养项目(2013721027);新疆自治区级大学生创新训练计划项目(201510758080)
蒋健楠(1991-),男,江苏江阴人,硕士生,主要从事水力学及河流动力学研究。E-mail:841157334@qq.com
牧振伟(1973-),男,河南南阳人,教授,主要从事水力学及河流动力学研究。E-mail:xjmzw@163.com

