徐变效应下桥梁钢管混凝土承载力变化规律的研究

卢伟升，杨为华

(1.湖南省交通规划勘察设计院，湖南长沙 410008;2.西安方舟工程咨询有限责任公司，陕西 西安 710075)

0 引言

1 钢管混凝土徐变的计算方法

钢管混凝土中的核心混凝土发生的徐变变形会使得构件截面应力重分布，在无外力作用的条件下并且忽略徐变过程中钢管对混凝土的紧箍作用，截面发生的这种应力重分布只是钢管混凝土结构体系内的应力重分布，所以可以得出:

随着徐变过程中混凝土变形增大，由于外包钢管约束着混凝土的径向变形，使得整个构件的变形相对减少，同时钢管的变形量会增大。从本质上讲，钢管混凝土的徐变是核心混凝土应力减少应变增大而钢管应力应变增大的过程［11］。图1 给出了徐变效应下钢管混凝土构件的变形图。

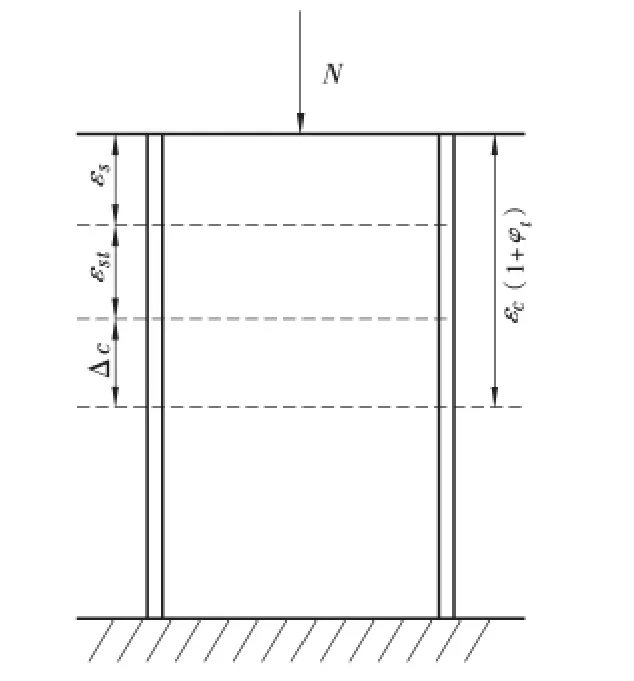
图1 钢管混凝土徐变变形图

其中，εc为徐变过程中核心混凝土应变增量;εst为徐变过程中钢管的应变增量;εc(1+φt)为假设核心混凝土不受钢管约束时徐变过程中的应变增量。

考虑钢管的约束作用，由于钢管与混凝土是统一构件，所以钢管的应变增量应等于核心混凝土的实际徐变增量，即εc=εs，此时变形增量为εs+εst。所以由于受到钢管的径向约束，使得总变形量减少了Δc。

产生徐变后，由公式(1)推得:

本文尝试将雷达图分析法应用在城市轨道交通规划及评价中。以天津地铁1号线为例，对车站周边土地利用特性、交通衔接条件及商业成熟度等影响车站客流的主要因素进行综合评价，构建基于雷达图分析法的评价函数，给出定量分析结果，并与实际客流表现进行比对，进而验证该方法的可行性。

徐变过程使得钢管混凝土产生了应力重分布［12］，这使得混凝土处于卸载的状态，构件截面上的应力是随时间不断减少的，假设核心混凝土的初始应力值为σ0，那么在徐变过程中的某一时刻，其应力值应变化为:

由式(2)，有:

其中，α 为含钢率。

代入式(3)，得:

1.1 弹性老化理论

弹性老化理论也称作流动率法，是一种改进后的老化理论。该理论将徐变函数看作是弹性变形、迟滞弹性变形以及流动变形三者之和。

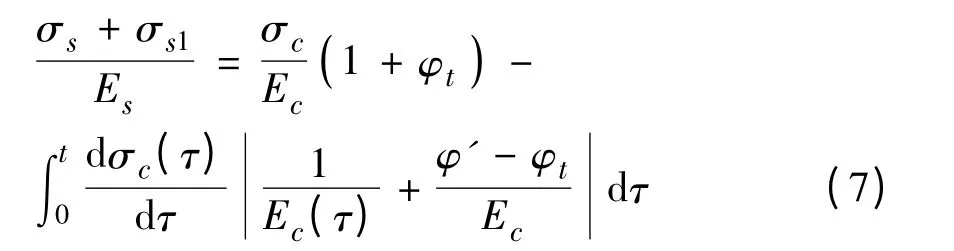
按中值定理:

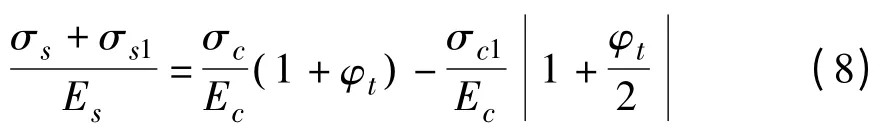
联立式(7)、式(8)，解得:

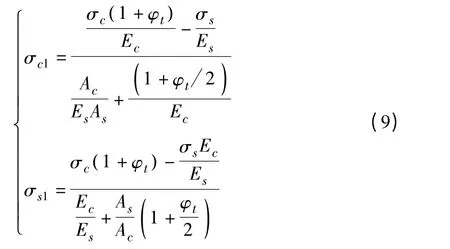
从而求解钢管混凝土的徐变应变为:

1.2 继效流动理论

继效流动理论假设应力水平较低，并且忽略混凝土的塑形变形，把徐变变形看作是瞬时弹性变形，不可恢复变形以及滞后变形之和。

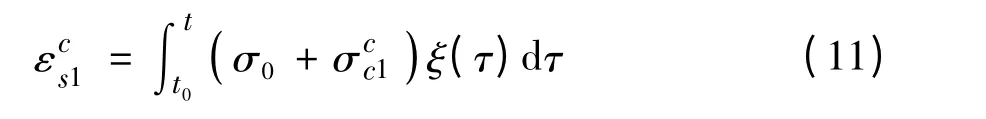
由于ξ(τ)的计算较为复杂，所以假设在t 时刻，钢管混凝土上发生的徐变变形值等于核心混凝土上作用的应力与徐变度的乘积。故式(11)可简化为:

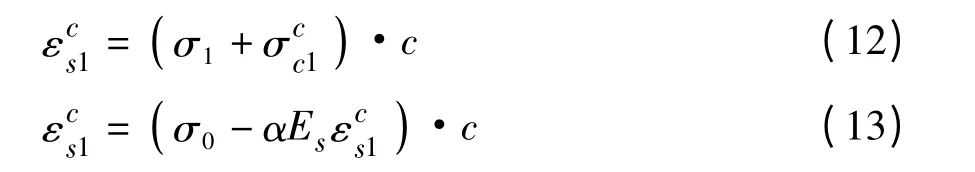
因此得出钢管混凝土构件在长期荷载作用下的钢管混凝土构件的徐变变形值:

2 徐变对钢管混凝土承载力的影响

利用ANSYS 软件建立钢管混凝土拱桥的有限元模型，分析了钢管混凝土拱桥在自重作用下的失稳形态，研究了长细比和含钢率对钢管混凝土徐变过程中的承载力变化的影响规律，并得出了相关结论。

2.1 钢管混凝土拱桥自重作用下的失稳模态

图2 给出了钢管混凝土拱桥发生失稳的4 种模态，依次为面外侧倾失稳，面外反对称失稳，面内反对称失稳，面内对称失稳。

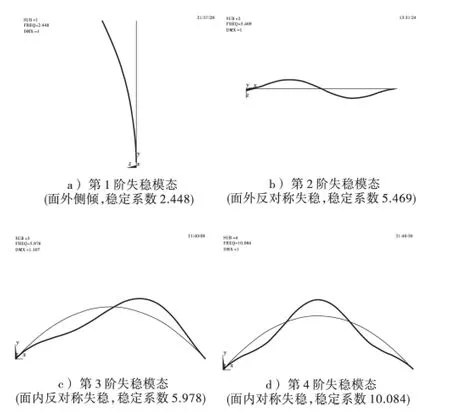
图2 自重作用下失稳模态

2.2 材料物理参数对钢管混凝土承载力变化的影响规律

本节建立的计算模型混凝土强度等级为C50。钢管混凝土的含钢率a 分别取0.08、0.10、0.12;长细比λ 取58、86、115、144、173，钢材型号取常见的Q235、Q345、Q390 号钢。为了能够更加直观的观察以上各参数在徐变过程中对钢管混凝土承载力的影响，这里取承载力影响系数kcr作为纵坐标。

其中，N'cr为考虑徐变作用时钢管混凝土的极限承载力;Ncr为不考虑徐变作用时钢管混凝土的极限承载力。

图3 为含钢率对kcr影响曲线图，从图中可以看出徐变对构件极限承载力有着非常显著的影响。相同含钢率条件下，在一定的范围内随着长细比的增大，钢管混凝土的影响系数开始先小幅增大，但整体上呈减小的趋势，且减小的速率逐渐变快;相同长细比的条件下，含钢率的增大导致影响系数的增大，这表明含钢率越大，徐变过程中钢管混凝土的承载力损失得越少。

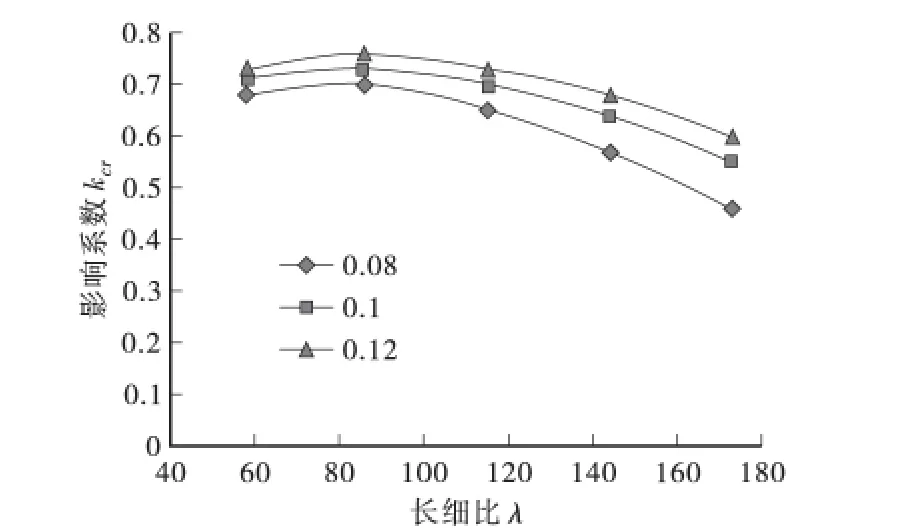
图3 含钢率对kcr的影响

发生这种现象是由于徐变能够使钢管提早进入塑性阶段，在材料和几何的双重非线性影响下，徐变使得结构变得越来越不稳定，故而承载力整体呈下降趋势。而当长细比在小范围内增加时，由于核心混凝土受压区的减少导致徐变作用相应地削弱，因而出现了小幅增大的现象。含钢率增大使得核心混凝土含量相对减小，这使得徐变变形减小，徐变对极限承载力的影响也随之减小。

图4 为钢材型号对kcr影响曲线图，从图中可以看出，在相同钢材型号的条件下，随着长细比在一定范围内增大，钢管混凝土的影响系数开始先缓慢的增大，达到一定程度后逐渐趋于稳定。相同长细比的条件下，不同的钢材型号对钢管混凝土承载力影响差别不大，在长细比增大到一定程度时，不同钢材型号对应的影响系数基本可以看作是相同的。

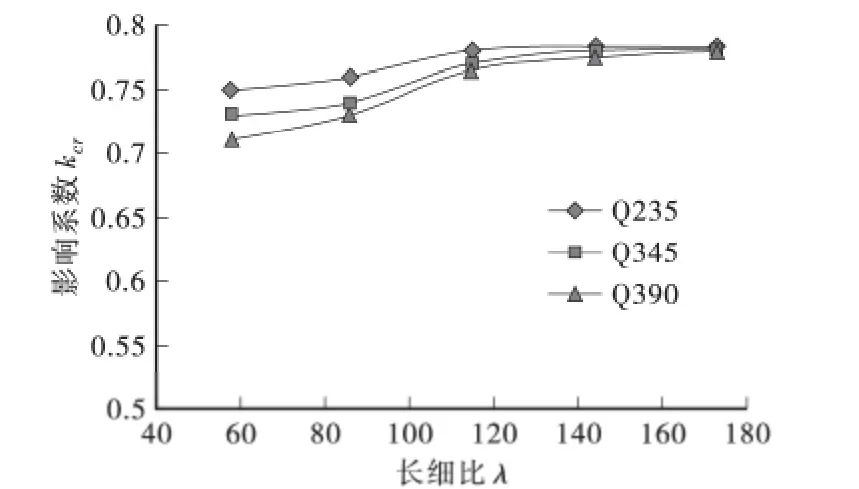
图4 钢材型号对kcr的影响

发生这种现象是由于钢材型号的改变并没有影响结构的整体刚度，所以结构的稳定系数是一致的，但是随着钢材型号的提高，钢管所能承受的荷载值提高，结构的极限承载力也在不断地增大，但由于钢材的含量相对较少，而徐变只对核心混凝土有影响，所以这种增长的趋势比较平缓。在长细比很大时，材料的强度已经不是结构破坏的主要因素，结构早已在材料屈服前由于失稳而破坏，所以kcr趋于稳定，不同钢材型号之间的承载力基本可以认为是一致的。

3 结论

1)本文阐述了钢管混凝土材料较一般钢筋混凝土材料在结构稳定和使用性能上的优越性，并基于已有研究成果，运用弹性老化理论和继效流动理论对桥梁钢管混凝土的徐变变形量公式进行了推导，得出了徐变效应下钢管混凝土变形量的理论解。

2)本文分别研究了长细比、含钢率以及钢材型号在徐变过程中对钢管混凝土承载力的影响规律，研究结果表明，相同含钢率条件下，随着长细比在一定的范围内增大，钢管混凝土的影响系数开始先小幅增大，但整体上呈减小的趋势，且减小的速率逐渐变快;相同长细比的条件下，含钢率的增大导致影响系数的增大;相同钢材型号的条件下，随着长细比在一定范围内增大，钢管混凝土的影响系数开始先缓慢的增大，达到一定程度后逐渐趋于稳定;相同长细比的条件下，不同的钢材型号对钢管混凝土承载力影响差别不大。

［1］胡曙光，丁庆军.钢管混凝土［M］.北京:人民交通出版社，2007.

［2］蔡邵怀.现代钢管混凝土结构(修订版)［M］.北京:人民交通出版社，2007.

［3］韩林海，杨有福.现代钢管混凝土结构技术［M］.北京:中国建筑工业出版社，2007.

［4］Furlong R W.Strength of steel-enased concrete beam columns［J］.Journal of the structural Division，ASCE，1967，93(5):113－124.

［5］Nakai H，Kudta A，Ichinose L.H.An Experimental Study Oil Creep of Concrete Filled Steel Pipes［C］.Proceedings of the 3rd International Conference Oil Steel-concrete Composite Structures.Fukuoks.Japan.1991.

［6］Nakai H，Kudta A，Ichinose L.H.An Experimental Study Oil Creep of Concrete Filled Steel Pipes［C］.Proceedings of the 3rd International Conference Oil Steel-concrete Composite Structures.Fukuoks.Japan.1991.

［7］Terrey P.J，Bradford M.A，Gilbert R.L.Creep and Shrinkage of Concrete in Concrete Filled Circular Steel Tubes［C］.Proceeding of 6th International Symposium on Tubular Structures.Melbourne.Australia.1994.

［8］Morino S，Kswangguchi J，Cao Z S.1996.Creep Behavior of Concrete Filled Steel Tubular Members［C］.Proc.Of Engineering Foundation Confer.On Steel Concrete Composite Structures.ASCE，Irsee.

［9］Uy B.Static Long-term Effects in Short Concrete Filled Steel Box Cloumns under Sustained Loading［J］.ACI Structural Journal，2001，98(1):96－104.

［10］Wassim Naguib，Amir Mirmiran.Creep Modeling for Concrete-filled Steel Tubes［J］.Journal of Constructional Steel Reasearch，2003，59:1327 ～1344.

［11］陈 勇.钢管混凝土拱桥徐变效应研究［D］.长沙:中南大学，2012.

［12］吴 波，瞿光义.钢管混凝土拱桥徐变产生的截面内力重分布计算［J］.西安公路学院学报，1991(4):21 ～25.