波流作用下圆柱体入水特性的三维数值模拟研究

杨 衡，孙龙泉，刘 莹，姚熊亮

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

波流作用下圆柱体入水特性的三维数值模拟研究

杨 衡，孙龙泉，刘 莹，姚熊亮

（哈尔滨工程大学 船舶工程学院，哈尔滨 150001）

结构在实际海况中入水受到多种载荷的共同作用，同时还伴随波浪作用的影响，因此该过程是一个强非线性的过程。针对结构在波、流中入水过程的特点，将入射波（波、流）引入非线性双渐进法，研究三维刚体圆柱体在波、流及波流联合作用下入水过程运动响应及姿态的变化，计算结果与试验结果符合得较好，非线性双渐进法适用于分析三维刚体波、流中入水问题。结果表明在近波面附近，结构受波浪作用明显，入水相位、浪级、流速及波流速度矢量差异对结构入水运动速度及轨迹影响明显。

入水；波流；非线性；双渐进法（DAA）

0 引 言

结构入水过程中会产生砰击现象，在真实的海况条件下，还要受到波浪、洋流的影响，结构入水过程中运动响应及姿态与波、流的传播方向、浪级和入水相位[1]有关，对结构入水过程的安全性及入水轨迹的稳定性非常重要。结构在波、流中入水，除受到浮力、结构自身重力、砰击载荷外，还要考虑到波、流载荷对结构的影响，同时还伴随波、流的运动及波面的非线性变化，因此该过程是一个强非线性瞬态流固耦合过程，包括湿表面、自由面边界条件和伯努利方程的非线性。

目前对入水砰击问题研究较多，研究对象以二维楔形体为主，自由液面多为自由平面。在国内外有关物体入水问题的研究文献中，真正考虑波浪因素的并不多，其中，Faltinsen[2]采用附加质量法计算入水物体所受水动力，基于势流边界元理论得出附加质量随浸深变化的关系曲线，并考虑入射波的作用，但未考虑入水物体对波浪的反作用。王文华等[3]采用二维CFD方法数值模拟了圆柱在规则波中的入水过程。储慧林[4]建立了二维数值水槽，重点研究了波浪相位及波高对鱼雷砰击压力、弹道和速度的影响。袁绪龙等[5]研究了具有细长前锥段外形的超空泡导弹在高速入水时弹道和流体动力的情况，通过流场-弹道耦合方法，分析了不同预置舵角下入水弹道与流体动力的变化规律。对于波浪因素的研究，权晓波等[6]基于波浪理论得到了二阶Stokes波的速度表达式，并通过给定入射边界速度分布形式的方法实现波浪的数值模拟，利用动网格技术、UDF技术等，探讨了水下航行体模型出水时波浪对其流场、力学特性等的影响。Wang和Wu[7]基于FEM方法求解了波浪与垂直固定圆柱体全非线性相互作用过程。刘云龙、张阿漫等[8]将波浪作用以入射势方式引入水下爆炸气泡计算中，得到气泡脉动与波浪面相互作用及波浪面的变形。对于潜射导弹出水、鱼类入水、水下爆炸气泡脉动等瞬态流固耦合领域，考虑流体的可压缩性是非常必要的，王诗平、孙士丽等[9]对可压缩流场中气泡脉动特性进行数值模拟，得出可压缩性对气泡射流速度的影响。王文华[10]利用液面捕捉法和直角切割网格系统解决入水过程中瞬时移动的自由液面和动边界问题。

本文的基于二阶双渐进法[11-13]（DAA2），推导了考虑入射波作用下二阶DAA方程，通过非线性伯努利方程[14]，将二阶DAA方程与结构运动方程耦合求解，讨论了刚体圆柱入水过程中运动特性，与模型试验进行对比，验证本文方法可靠性。着重探讨了波、流作用下三维结构入水特性，为进一步研究海洋结构物在波浪中入水问题提供了方法。

1 数值计算方法

水中的结构物与流场的瞬态耦合问题有这样的特点：早期瞬态（高频）响应主要是声辐射问题，即所谓平面波或曲面波近似解问题；后期瞬态(低频)响应主要是“虚质量”问题。Geers等人（1975-1980），根据这些特点提出了双渐近法（DAA）。双渐近法（DAA）之所以能广泛应用于水中结构物瞬态流固耦合领域，其中一个重要原因是它考虑了流体可压缩性，假设流场为各向同性、无粘、无旋但可压缩的理想流体，则考虑可压缩性的势函数微分方程式：

建立结构在波、流中入水数值计算模型如图1所示，结构以速度V在重力作用下垂直入水，波、流向右传播。

结构运动的边界条件为：

式中：V为结构运动速度；n是法向矢量坐标；Φi为波浪产生的速度势。

无穷远的边界条件为：

当考虑自由液面效应时，流场在满足控制方程以及物面不可穿透条件的同时，还需满足自由液面边界条件：

运动学边界条件：

图1 数值模型Fig.1 Calculate model

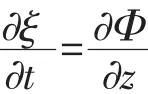
动力学边界条件：

式中：g为重力加速度，ξ为自由液面的波幅。

在延迟势法基础上，满足上述边界条件，求解控制方程（1），得到速度势方程如下：

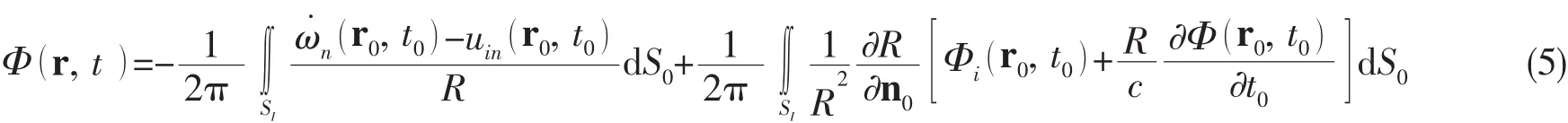
in标r0的距离。

引入了一个线性假设，P=（ρΦ˙r,）t，得到考虑入射波作用下双渐近方程如下：

其中：P=Ps+Pb，Ps为流体中的散射压力，Pb为入射波压力。

将方程（6）对时间进行一次积分

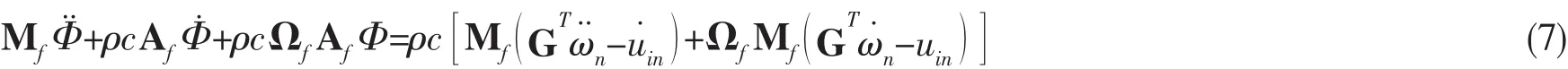
在得到流场速度势的基础上，可以通过非线性伯努利方程[11]得到流场压力计为Pd。

将计算所得的动压力加载到结构上，得结构动响应。

结构运动速度ω˙n以及结构加速度ω¨n作为下一次计算的初值，从而完成下一次循环计算。

2 波浪作用下结构入水特性

2.1 波浪基本理论

波浪是海面受风压扰动后,在重力作用下产生的周期性运动，粘性的作用很小。当模型尺度相对于波浪波长较小，不规则波浪可简化为规则的三维平面进行波。波浪运动采用空间固定坐标系OXYZ，波浪向X轴正向传播，如图2所示。

波数k=2π/λ，频率ω=2π/T，T为波浪周期。

线性波速度势为：

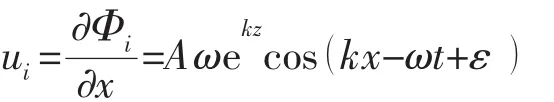
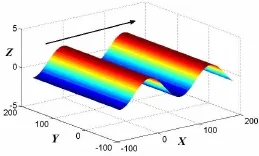
图2 三维波浪示意图Fig.2 The 3D wave

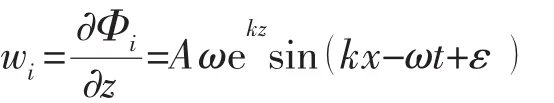
2.2 模型试验结果对比分析

应用本文方法计算，选取与文献[11]具有相同的质量，质心位置，转动惯量计算模型，计算该圆柱缩比模型入水过程中运动参数变化，并与试验值进行对比分析。图3给出结构入水过程中运动速度及姿态计算值与试验值对比结果。

图3是圆柱入水过程中三个方向的速度变化曲线，V1是横向速度、V2法向速度、V3是垂向速度，从图中可以看出，结构入水过程中受到的垂向载荷变化剧烈，结构的垂向加速度变化剧烈，相比于垂向速度和法向速度，横向速度的变化曲线最为平缓。

图4、5是结构入水过程中俯仰角、偏航角的变化曲线，从中可以看出，在圆柱入水过程中，在砰击载荷和波浪载荷的作用下，圆柱俯仰角减小；偏航角增大，即圆柱在入水过程中首部受力和尾部受力的不平衡产生了偏转力矩，引起了圆柱运动姿态的改变。

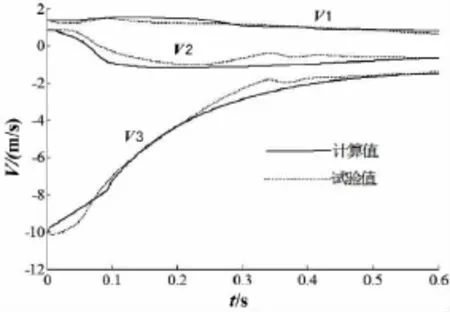
图3 速度时历曲线Fig.3 The history curve of the velocities

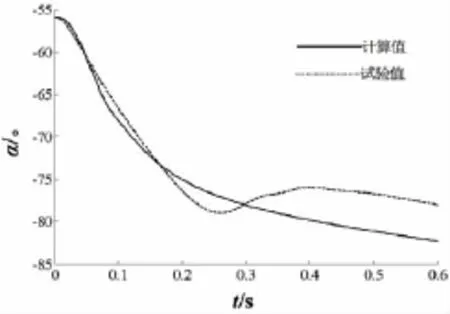
图5 偏航角时历曲线Fig.5 The history curve of the yaw angle

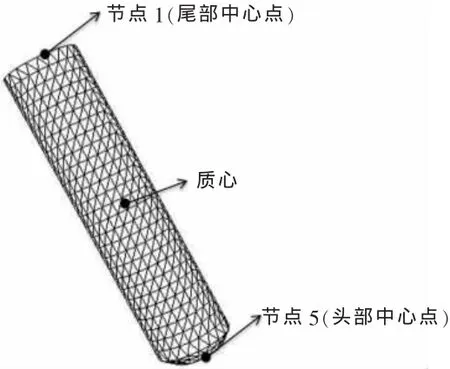
图6 节点分布Fig.6 The distribution of note

2.3 波浪作用下圆柱入水运动特性分析

选取波浪浪级为5级，取上述计算模型，垂直入水速度为25m/s，水平速度为0，入水位置为波谷，波浪向右传播。取圆柱体三个特征点：头部、尾部中心点、质心进行，如图6所示。

计算过程中忽略波面变形及气垫效应对圆柱入水特性影响，计算结果如图7和图8所示。

由图7可以看出，圆柱在波浪中入水过程三个节点的运动速度呈现明显的差异，头部中心点（节点5）首先入水，受到波浪作用，头部质点速度增加，随着侵水深度的增加，波浪作用力减小，头部速度增加变缓。在圆柱质心入水前，圆柱头部处于波浪作用，产生相对于质心逆时针弯矩，使圆柱尾部产生反向速度；圆柱质心入水后，一方面圆柱尾部逐渐侵水，受到波浪作用，另一方面圆柱头部远离波浪面，波浪作用力减小，两者共同作用结果产生绕圆柱顺时针弯矩，圆柱尾部速度逐步恢复至零值。圆柱质心速度与圆柱头部质心速度变化趋势相近。从图8可以看出，波浪作用对圆柱垂向速度影响较小，在圆柱头入水和尾入水瞬间，垂向速度曲线产生明显的波动。由以上分析，可将圆柱体在波浪中入水过程分为三个明显的过程：

（1）头入水—质心入水：圆柱头部中心、质心速度正向增加，尾部速度负向增加；

（2）质心入水—尾入水：圆柱头部中心、质心速度正向增加，尾部速度负向减小；

（3）尾入水—：尾入水时刻，圆柱三点的速度出现波动，随着圆柱继续下沉，波浪的作用减弱，各点速度变化平稳。由于波浪引起的水质点运动主要集中在近水面的区域内，在距水面较远处波浪对圆柱运动的影响基本可以忽略。

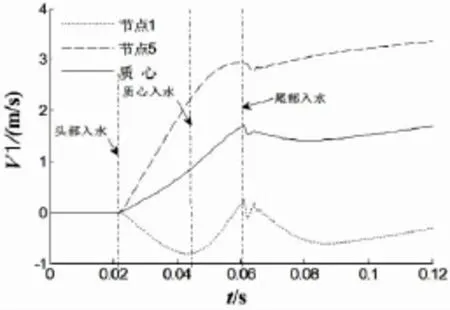
图7 圆柱在波浪中入水各点横向速度对比Fig.7 The comparison of the horizontal velocities of water entry in wave

图8 圆柱在波浪中入水各点垂向速度对比Fig.8 The comparison of the vertical velocities of water entry in wave

2.4 不同波浪相位下圆柱入水运动特性分析

对于无限水深平面进行波，波浪在同一竖直线上的水质点做同相位的圆轨线运动，处于波峰A点、波节B点和波谷C点的水质点的速度如图9所示，调整波面方程中相位角ε可使圆柱处于波峰、波节和波谷三个入水位置，计算不同相位下，圆柱体入水过程运动特性。

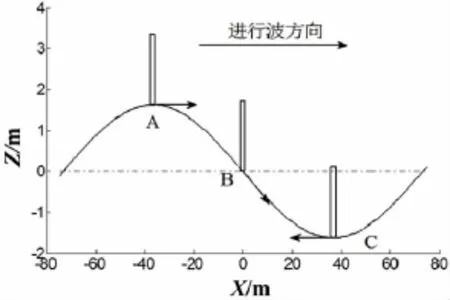
图9 不同入水位置示意图 Fig.9 The sketch of different entry location

图10 俯仰角及偏航角定义Fig.10 The definition of the pitch angle and the yaw angle

本文对结构入水姿态的描述采用与出水问题相近的偏航角与俯仰角，其定义如图10所示，偏航角定义为结构纵轴与大地坐标系X轴正向之间的夹角θ，偏航角定义为结构质量中心与初始点之间连线与Z轴负向之间夹角α，结构向X轴正向偏转时俯仰角和偏航角为正向。

由图11可以看出，由于波浪波峰与波谷处水质点运动速度相反，圆柱体在波峰与波谷入水时产生相反的运动轨迹，相同的入水速度及计算时间范围内，波谷入水时，圆柱体横向运动距离大于波峰入水情况，波节处入水情况下圆柱体横向运动距离最小，其运动规律与波谷入水情况相似。图12给出不同相位处圆柱体入水过程横向速度变化，其决定质心横向运动的距离，三个入水相位中，波谷入水时横向速度峰值最大。图12中第一个速度峰值时刻对应圆柱体头部完全入水时刻，第二个速度峰值时刻对应圆柱质心垂向运动位移等于半个波幅值时，当圆柱体质心垂向运动位移等于波幅后，波浪影响逐步较小，圆柱体质心横向速度变化平缓。

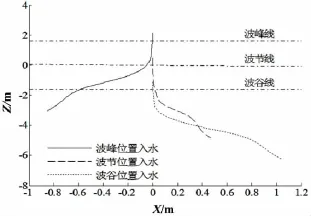
图11 质心运动轨迹Fig.11 The motion track of the center of mass

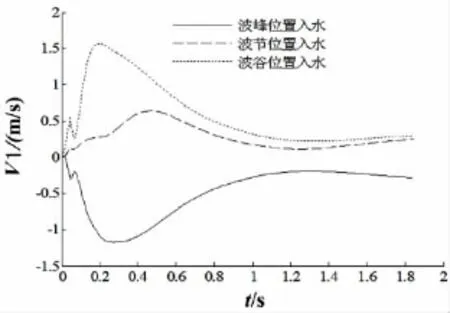
图12不同相位处入水质心横向速度比较Fig.12 The comparison of the horizontal velocities of water entry in different phase

图13、14给出圆柱在不同相位入水时，圆柱入水及水中运动过程俯仰角与偏航角变化情况，圆柱在三个相位处入水时，均产生明显的偏航角，在近波面，圆柱体受到波浪的影响较大，俯仰角变化速率较大，随入水深度增加，波浪的影响逐渐较小，圆柱体在表面压差的作用下，俯仰角继续减小甚至发生倾覆。偏航角表征圆柱体入水过程结构质心偏离初始位置情况，表明入水过程横向载荷的变化。由图14可以看出，圆柱体在不同相位处入水偏航角变化不同，波峰入水与波节、波谷入水产生相反的偏航角，波峰入水时的偏航角最大值大于波峰入水，波节入水过程中偏航角变化最小。随入水深度增加，波浪的影响逐渐较小，偏航角逐渐趋于平衡。

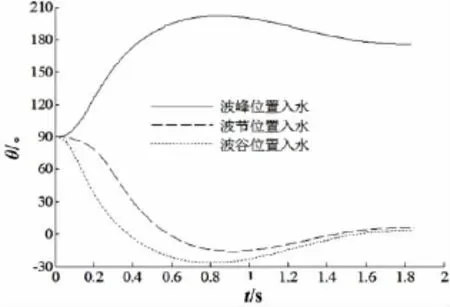
图13 不同相位处入水俯仰角比较Fig.13 The comparison of the pitch angle of water entry in different phase

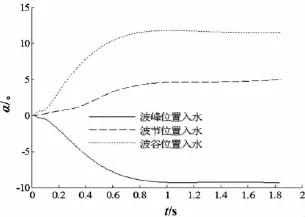
图14 不同相位处入水偏航角比较Fig.14 The comparison of the yaw angle of water entry in different phase

2.5 浪级对圆柱入水运动特性影响

为了研究不同浪级对结构入水影响，选取波高、周期如图15所示规则波，圆柱接触水面时的波浪正处于波谷位置。

图16给出圆柱在不同浪级作用下入水过程横向对比曲线。随着浪级的增大，圆柱入水过程中质心横向速度明显增加。

图17给出圆柱在不同浪级下俯仰角对比，随着浪级的增大，圆柱入水过程俯仰角增加，波浪诱导结构产生的俯仰力矩大于横向载荷，浪级变化作用对结构入水姿态影响明显。

图15 不同浪级示意图Fig.15 The sketch of different wave scale

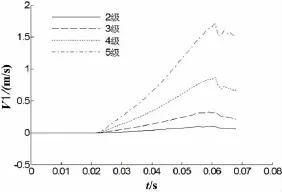
图16 不同浪级入水横向速度对比Fig.16 The comparison of the horizontal velocities of water entry in different wave scale

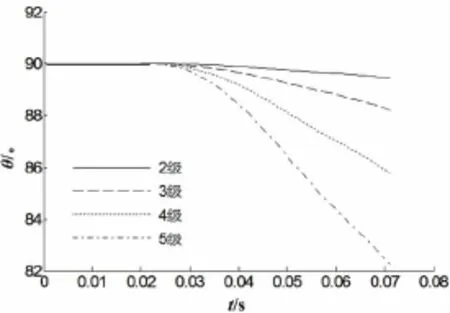
图17 不同浪级入水俯仰角对比Fig.17 The comparison of the pitch angle of water entry in different wave scale

3 海流作用下结构入水特性

海流又称洋流，是海水在地转偏向力、引潮力等作用而产生的相对稳定的大规模稳定的流动，因此，可将海流简化为均匀流。计算时取垂直入水速度为25 m/s，均匀流向右传播，流速度为2.0 m/s。下图给出均匀洋流作用下圆柱体入水过程三个节点横向速度和垂向速度比较。

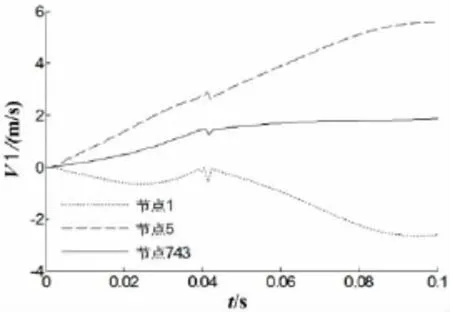
图18 横向速度对比Fig.18 The comparison of the horizontal velocities

图19 垂向速度对比Fig.19 The comparison of the vertical velocities

由图18可以看出，在均匀流作用下圆柱体入水过程也存在三个明显的拐点，即头部（节点5）入水、质心（节点743）和尾部（节点1）入水三个时刻。在尾部入水时刻，三个特征节点的横向速度出现明显的波动，因为在圆柱体全部入水后，附加质量变化率在此时刻忽然变为零。在整个入水过程中，头部质心（节点5）较尾部质心（节点1）变化剧烈，圆柱质心的横向速度在整个入水过程中逐渐趋于洋流速度2.0 m/s。圆柱体三个特征节点的垂向速度在尾部入水前并未出现明显变化，在尾部入水时刻出现波动，之后继续下降。在圆柱体全部入水后，在自身重力和浮力作用下，且此时圆柱体偏转角度较大，三个节点的垂向速度发生较大的差异。

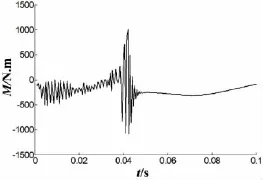
图20 俯仰力矩变化曲线 Fig.20 The history curve of the moment

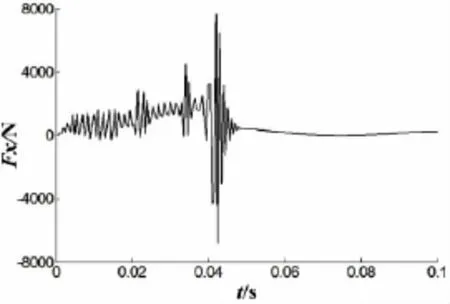
图21 水平合力变化曲线Fig.21 The history curve of the horizontal force

图20给出圆柱体入水过程中绕圆柱体质心俯仰力矩变化，由图可以看出，俯仰力矩在尾部入水前为负值，随着入水深度的增加，圆柱体质心上部和下部压力分布逐步均匀，俯仰力矩并逐步减小。在尾入水时刻，俯仰力矩波动较大。完全入水后，由于圆柱体表面仅受到静水压力的影响，上下载荷分布较均匀，俯仰力矩变化较平缓。图21给出圆柱入水过程中水平方向合力的变化，由图可以看出，圆柱体入水深度增加，水平合力逐渐增大，在尾部入水时刻，水平合力出现较大波动。在圆柱体完全入水后，由于迎、背流面压差仅为静水压力所造成的压差，其相差较小，因此，合外力变化较小且趋于零值。

针对不同流速下圆柱体入水影响，分别选取流速为0.5 m/s、1.0 m/s、1.5 m/s及2.0 m/s，计算不同流速下圆柱体的运动状态与载荷特性。图22给出不同流速下圆柱体入水过程中水平速度对比。

由图22可以看出，随洋流速度增大，圆柱体入水质心水平方向速度增大，且逐渐趋于流速，圆柱体完全入水后，质心水平速度变化趋于平缓。下图给出不同流速下圆柱体入水过程中俯仰角和偏航角对比。

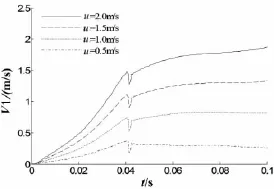
图22 水平速度对比Fig.22 The comparison of the horizontal velocities

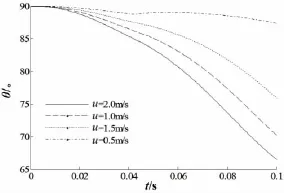
图23 俯仰角对比Fig.23 The comparison of the pitch angle

图24 偏航角对比Fig.24 The comparison of the yaw angle

由图23、24可以看出，随洋流速度增大，圆柱入水过程的俯仰角和偏航角越大，即俯仰力矩和水平合力越大。在整个入水过程中，俯仰角和偏航角随流速增加变化越剧烈。

4 波与流共同作用下结构入水分析

在实际海况下，波与流往往是同时存在的，在计算实际海况下结构入水问题，要考虑波与流共同对结构物的作用。相对于船舶与海洋结构物的尺度，海洋中海流的尺度较广，且沿水深变化较小，因而可将波、流共同作用下结构入水简化为波浪与均匀流共同作用下结构入水问题。

4.1 波与流速度矢量共线

分别选取洋流速度与波浪传播方向同向和逆向两种形式，波浪浪级取为3级、洋流速度取为1.5 m/s，计算波流共线时圆柱体入水过程运动特性。图25给出不同流速下圆柱体入水过程中水平速度对比。

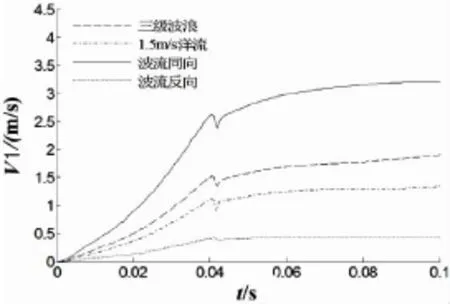
图25 水平速度对比Fig.25 The comparison of the horizontal velocities

由图25可以看出，在波流共同作用下，圆柱体入水过程运动特性与姿态发生较大变化。三级海浪的作用效果大于1.5 m/s流速，波流同向时增大了圆柱体质心的横向速度，波流反向时，抑制了圆柱体横向速度变化，由于波浪的作用大于流速，圆柱体质心横向速度仍为正向。下图给出不同流速下圆柱体入水过程中俯仰角和偏航角对比。

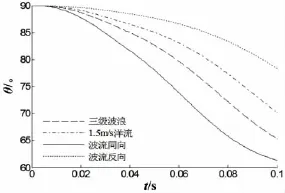
图26 俯仰角对比Fig.26 The comparison of the pitch angle

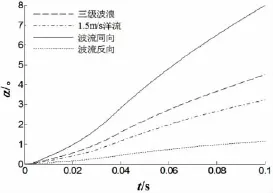
图27 偏航角对比Fig.27 The comparison of the yaw angle

由图26、27可以看出，波浪、洋流、波流共同作用四种情况下，圆柱均按顺时针方向绕质心做俯仰运动，波流同向时俯仰角和偏航角最大，反向时最小。在给定波浪等级和洋流速度情况下，仅有波浪作用时圆柱体的俯仰角、偏航角大于仅有洋流作用时俯仰角、偏航角。

下图给出不同流速下圆柱体入水过程中俯仰角速度和偏航角速度对比。

28俯仰角速度对比Fig.28 The comparison of the pitch angle velocity

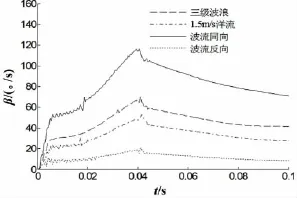
图29 偏航角速度对比Fig.29 The comparison of the yaw angle velocity

由图28、29可以看出，波流的共同作用下，俯仰角速度增加到最大值的时刻提前，在相同的入水时间条件下，波流共同作用下圆柱体俯仰角速度逐渐减小为零，而偏航角速度变化规律相同。

4.2 波与流速度矢量相差90°

实际海洋环境下，波与流的传播方向有时并不同向，本节选取波浪传播方向沿X轴正向，流传播方向沿Y正向，计算波与流传播方向不同时结构入水运动特性，并与仅存在波浪和仅存在洋流作用下圆柱入水特性进行对比。

图30给出仅存在波浪、仅存在洋流及波流共同作用下圆柱质心位置变化。

由图30可以看出，仅存在波浪时，质心偏移方向沿X轴正向，仅存在洋流时，质心偏移方向沿Y正向，波流共同作用时，质心运动偏转方向根据浪级的大小和流速大小确定。

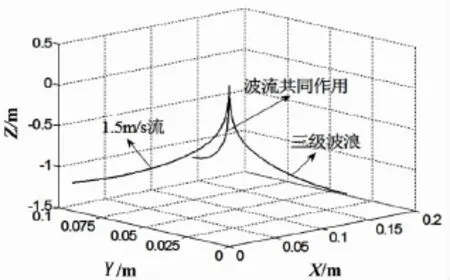
图30 质心位置对比Fig.30 The motion track of the center of mass

5 结 论

本文采用非线性双渐进法对圆柱非定常入水过程进行模拟，计算值与试验值吻合较好，本方法适用于三维入水问题求解。通过对波、流及波流载荷共同作用下三维刚体结构入水运动、姿态变化特性得到以下结论：

（1）圆柱入水过程中，存在两个关键时刻，尾部入水瞬间和头部入水瞬间，对结构运动速度产生明显的影响。在这两个时刻，入水砰击力存在峰值，其本质原因是在入水过程中附加质量的剧烈变化，也就是湿表面的剧烈变化。

（2）不同波浪相位入水时，圆柱体的运动轨迹与姿态差异较大，波峰入水与波节、波谷入水俯仰与偏航运动相反；波浪浪级增大加剧圆柱体的运动的偏移。

（3）在近波面，波浪对结构作用效果明显，结构完全入水后，波浪作用效果逐渐减弱。同时波浪载荷对结构轴向载荷影响较横向载荷小。

（4）同流速对结构入水产生明显影响，流速越大，圆柱体入水速度和姿态变化越剧烈。

（5）波流共同作用下，结构入水特性改变，波流同向加剧圆柱入水姿态变化，波流反向抑制圆柱体入水姿态变化，波流流向不共线时，圆柱体产生两方向俯仰与偏航运动。

[1]殷崇一.潜射导弹发射与出水载荷研究[D].西安:西北工业大学,2004．Yin Chongyi.Research on launch and effluent load of submarine-launched missile[D].Xian:Northwestern Polytechnical University,2004．

[2]Faltinsen O M.Sea loads on ships and offshore structures[M].UK:Cambridge University Press,1990.

[3]王文华,王言英.圆柱在波浪中入水的数值模拟[J].上海交通大学学报,2010,44(10):1393-1399. Wang Wenhua,Wang Yanying.Numerical study on cylinder entering water in wave[J].Journal of Shanghai Jiao Tong University,2010,44(10):1393-1399.

[4]储慧林.鱼雷在波浪中入水的数值模拟[D].镇江:江苏科技大学,2014．Chu Huilin.Numerical simulation of torpedo entering water in wave[D].Zhenjiang:Jiangsu University of Science and Technology,2014．

[5]袁绪龙,朱 珠.预置舵角对高速入水弹道和流体动力的影响[J].应用力学学报,2015,33(1):11-16. Yuan Xulong,Zhu Zhu.Influence of preset rudder angle on trajectory and hydrodynamic at high-speed water-entry[J]. Chinese Journal of Applied Mechanics,2015,33(1):11-16.

[6]权晓波,孔德才,李 岩.波浪模拟及其对水下航行体出水过程影响[J].哈尔滨工业大学学报,2011,43(3):140-144. Qüan Xiaobo,Kong Decai,Li Yan.Wave simulation and its effects on the exceeding water process of the underwater vehicle[J].Journal of Harbin Institute of Technology,2011,43(3):140-144.

[7]Wang C Z,Wu G X.Interactions between fully nonlinear water waves and cylinder arrays in a wave tank[J].Ocean Engineering,2010,37:400-417.

[8]刘云龙,张阿漫,王诗平,田昭丽.基于边界元法的气泡同波浪相互作用研究[J].物理学报,2012,61(22):1-8. Liu Yunlong,Zhang Aman,Wang Shiping,Tian Zhaoli.Research on interaction between bubble and surface waves based on BEM[J].Acta Phys.Sin.,2012,61(22):1-8.

[9]王诗平,孙士丽,张阿漫,陈 玉.可压缩流场中气泡脉动数值模拟[J].力学学报,2012,44(3):513-520. Wang Shiping,Sun Shili,Zhang Aman,Chen Yu.Numercal simulation of bubble dynamics in compressible fluid[J].Acta Mechanica Sinica,2012,44(3):513-520.

[10]王文华,黄 一,王言英,翟钢军,黄亚南.弹性楔形体各状态参数对入水运动性能的影响[J].船舶力学,2014,18(11): 1320-1330.Wang Wenhua,Huang Yi,Wang Yanying,Zhai Gangjun,Huang Yanan.Effect of status parameters for elastic wedge on dynamic performance of water-entry[J].Journal of Ship Mechanics,2014,18(11):1320-1330.

[11]Geers T L.Residual potential and approximation methods for three dimensional fluid-structure interaction problems[J].J Acoust.Soc.Amer.,1971,49:1505-1510.

[12]Geers T L.Doubly asympotic approximation for transient motions of submerged structures[J].J Acoust.Soc.Ame.,1978, 64:1500-1508.

[13]Geers T L,Felippa C A.Doubly asymptotic approximations for vibration analysis of submerged structures[J].J Acoust.Soc. Amer.,1980,73:1152-1159.

[14]孙士丽.具有自由液面效应的高频流固耦合问题[D].哈尔滨:哈尔滨工程大学,2010. Sun Shili.The high frequency fluid structure interaction problems with free surface effect[D].Harbin:Harbin Engineering University,2010.

3D numerical simulation on water entry of cylindrical under wave and stream action

YANG Heng,SUN Long-quan,LIU Ying,YAO Xiong-liang
(Harbin Engineering University,Haerbin 150001,China)

During water entry of the structure in actual sea states,it will receive the interaction of a variety of loads,as well as the influence of wave and stream action,so this is a strong non-linear process.According to the characteristics of water entry of the structure,the incident wave and stream will be introduced to the nonlinear doubly asymptotic approximation method,so as to study the motion response and attitude change of 3D rigid cylindrical under wave and stream action during water entry.The calculation results fit with the test results well,this method is available for the analysis of water entry of 3D rigid body.The results show that in the vicinity of wave surface,the wave affects the structure distinctly;phases of water entry,wave scale,stream velocity and the differences of wave and stream velocities vector influence the speed, motion trajectory of the structure in water notably.

water entry;wave and stream;non-linear;DAA(doubly asymptotic approximation)

U671.5

A

10.3969/j.issn.1007-7294.2015.10.003

1007-7294（2015）10-1186-11

2015-05-03

船舶预研支撑技术基金资助项目（13J1.5.1）；国家自然科学基金资助项目（51309060）

杨 衡（1986-），男，博士研究生，E-mail:yanghengmvp@163.com；孙龙泉（1983-），男，讲师。