基于总应变能的多轴疲劳模型研究

孙楠楠，李国祥，白书战，王洋，魏涛

（1山东大学能源与动力工程学院，济南250061；2潍柴动力股份有限公司技术中心，山东潍坊261205）

基于总应变能的多轴疲劳模型研究

孙楠楠1，李国祥1，白书战1，王洋2，魏涛2

（1山东大学能源与动力工程学院，济南250061；2潍柴动力股份有限公司技术中心，山东潍坊261205）

该研究提出一种多轴疲劳寿命预测模型。结合现有的几种多轴疲劳模型的优点和不足之处，分别对正应变能部分和剪应变能部分做出了修正，提出了一个能够适用于多种载荷形式的多轴疲劳寿命预测模型。该模型通过求解莫尔圆把剪应变幅作为临界面判定参量，把临界面上的总应变能作为损伤参量。运用SNCM630合金钢、纯钛和钛合金等4种材料的疲劳试验数据对提出的模型进行评估和验证，尽管材料特性和载荷形式各异，但所有的预测寿命基本都落在了试验寿命两倍的公差带以内，这证明提出的新模型具有较高的预测精度。

多轴疲劳；能量准则；临界面；多轴比例—非比例载荷

0 引言

随着对弹塑性力学和疲劳裂纹萌生机理的深入研究，基于应变的疲劳寿命模型研究得到了很好的发展，弥补了S-N方法只基于统计数据但缺乏深入的理论基础的弊端。目前商业软件中已经将Manson-Coffin模型、Morrow模型、SWT模型等单轴模型引入了结构件的应用当中并取得了良好的效果。发动机结构件在工作过程中几乎都是处于多轴应力状态下的，但是目前仍然没有一个公认的多轴疲劳寿命模型。目前的多轴疲劳寿命模型主要分为三类：应力模型、应变模型和应变能模型。无论应力、应变模型还是能量模型，与临界面法结合都是目前最流行且最有效的方法。KBM模型、Wang-Brown模型、Fatemi-Socie模型都是结合临界面法的有效的应变模型，国内也有王英玉、尚德广、李静、吴志荣等提出了几种非常准确的基于应变和临界面的多轴模型。但是基于应力和应变的临界面法因为缺乏严格的连续动力学理论基础而饱受质疑，因此本研究是在连续动力学和弹塑性力学的基础上，把应变能作为疲劳损伤参量进行了深入的研究。本研究是在参考了SWT[1]、Glinka[2-3]、Chen[4]、Fatemi-Socie[5]、Varani-Farahani[6]等模型的基础上，提出了一种新的适用于多轴比例/非比例载荷的应变能模型。新模型不但考虑了平均正应力、平均剪应力的影响，还考虑了多轴比例/非比例载荷强化效应。本研究还通过文献中的大量试验数据，验证了新模型的准确性。

1 新模型的提出

1.1 临界面的确定

自从临界面的思路被Brown和Miller等提出，由于它的有效性和准确性，该方法得到了很好的发展。目前临界面的判定有基于应力、应变和应变能等方法。经过对比研究，新模型把剪应变幅作为临界面的判定参量。本研究以薄壁圆管作为简化的研究对象，通过应力—应变的莫尔圆得到应力应变的弹塑性张量：

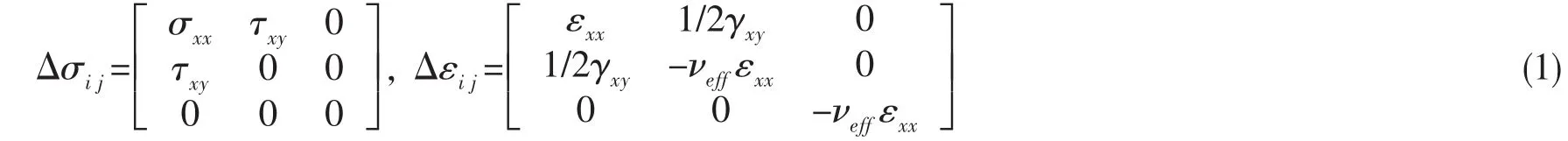
文献[7-9]中给出了详细的推导过程，基于最大剪应变幅的临界面的具体求解表达形式为：

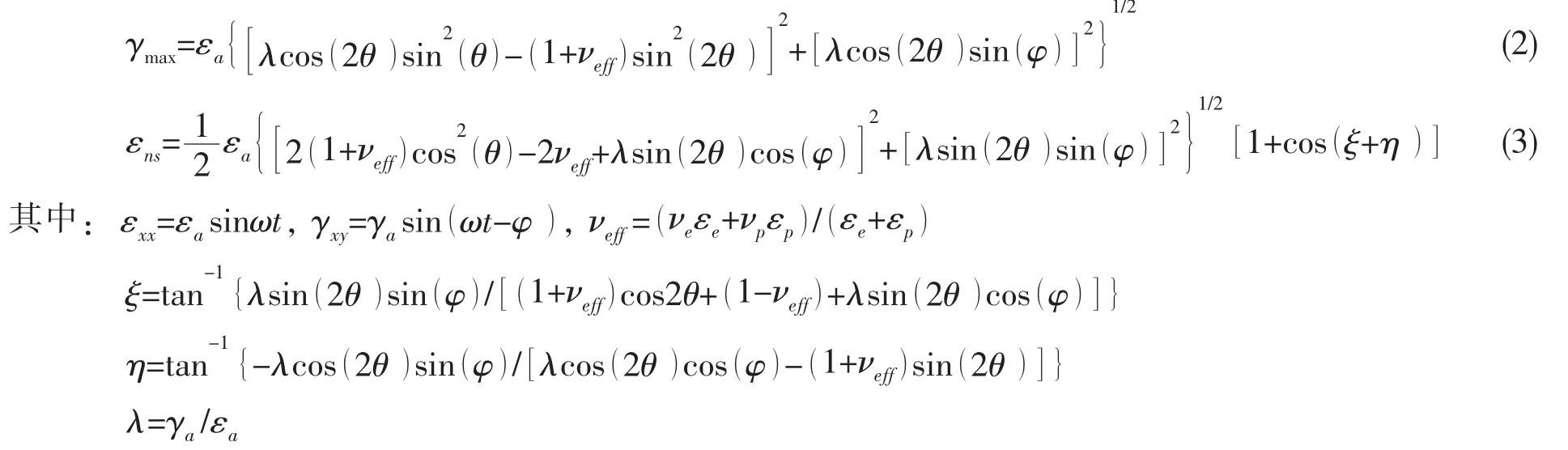
式中：εa为正应变幅，γa为剪应变幅，θ为相位差，εe和εp分别为弹塑性应变。

1.2 新模型的推导

新模型中的损伤参量由正应变能和剪应变能两部分组成，本研究分别对两部分作出改进和推导。

1.2.1 正应变能部分

Sines等人[10]在其研究中指出：在拉压载荷下，平均拉应力能够加速疲劳的发生，而平均压应力能够延长疲劳寿命，如图1（a）所示。现有的模型中，也大都已经考虑到了平均正应力的影响，如现在已经被疲劳软件采用的Morrow模型和SWT模型都考虑了平均正应力修正。文献[11]中的对比研究表明：基于应变能的SWT模型能够比基于应变的Morrow、Manson-Coffin模型更加准确地预测高低周疲劳，SWT模型公式如下：

SWT模型主要有两个缺点：（1）该模型的疲劳损伤参量过度重视了平均应力而忽略了应变幅对疲劳寿命的决定性作用，当平均正应力的值太大时，SWT模型就不再能准确预测疲劳寿命，文献[11]中证明了这一点。（2）Bergmann等人[12]通过研究发现，平均应力对弹塑性阶段的影响是不一样的，平均应力对弹性阶段的影响程度要强于对塑性阶段的影响，而SWT模型对平均正应力的修正没有考虑到这一点。基于上述两点考虑，对SWT模型进行变形：

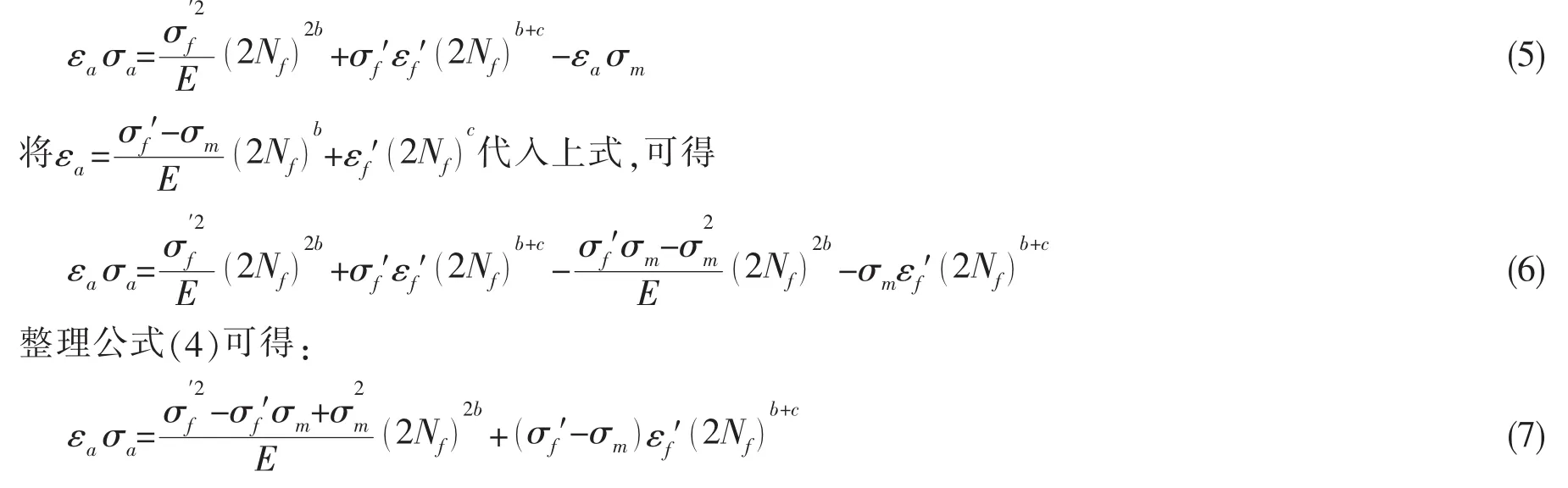
式中：σf′为疲劳强度系数，b、c分别为疲劳强度指数和疲劳延性指数，εf′为疲劳延性系数，E是弹性模量，σa为正应力幅，σm为平均正应力。

1.2.2 剪应变能部分

基于Glinka[2-3]和Chen[4]模型，剪应变能部分可用如下公式表达：

Sines等人证明了正应力对扭转疲劳和拉压疲劳的作用是一致的，如图1（b）所示，却认为平均剪应力对疲劳寿命没有影响。但是Papadopoulos[13]、Dang Van[14]、Liu[15]、McClaflin和Fatemi[16]等人都通过研究证明了平均剪应力会使疲劳寿命缩短。考虑平均剪应力的影响，可将公式（8）改写成如下形式：

考虑到正应力对单轴扭转疲劳的影响，在损伤参量中引入正应力修正参数（1+σm/σf′），则剪应变能部分最终的表达形式如下：

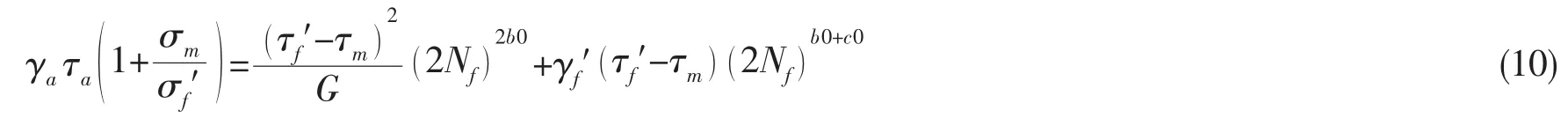
式中：τf′为剪切疲劳强度系数，b0，c0分别为剪切疲劳强度指数和剪切疲劳延性指数，γf′为剪切疲劳延性系数，G是剪切模量，τa为剪应力幅，τm为平均剪应力。

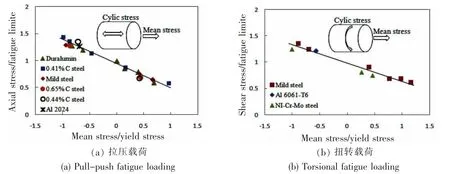
图1 平均正应力对疲劳强度的影响Fig.1 The effect of axial mean stress

1.2.3 多轴模型

经过前面两个部分对正应变能部分和剪应变能部分的推导，多轴疲劳模型的基本形式为：

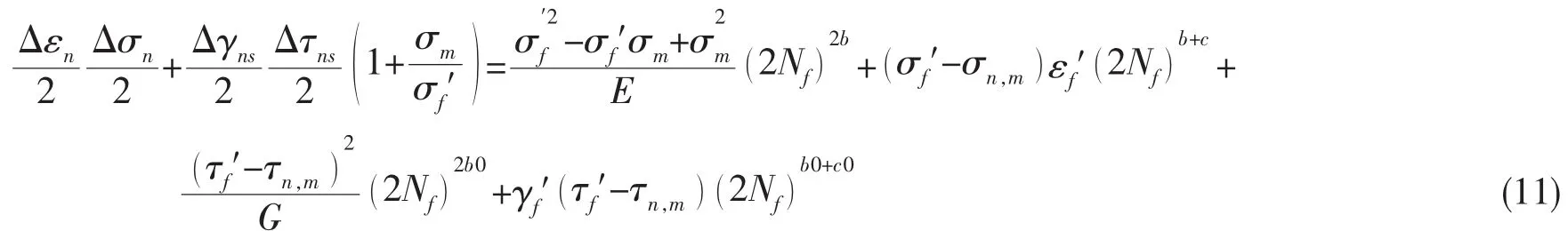
但是多轴载荷下的疲劳寿命预测模型不仅是前面两部分的简单组合，还要考虑多轴作用及非比例强化效应。特别是在非比例载荷下，应力应变主轴方向的变化会导致更多位错的发生和滑移带的形成，从而加速疲劳过程。Socie和Marquis等人[17]曾在其研究中发现，在应变幅不变的情况下，相位差意味着更多的应变能，因此在疲劳模型中需要引入参数修正非比例效应。Fatemi和Socie[5]在FS模型的损伤参量的中提出修正参数（1+nσn，max/σy）来体现多轴及非比例效应，后来Varvani-Farahani等人[6]又针对此修正系数的不足进行了改进，将参数修改为（1+σn，m/σf′）。本研究发现临界面上的平均正应力为零时，σn，m=0时，Varvani-Farahani的修正参数无法体现正应力对剪应变能的影响，因此多轴模型中将剪应变能部分的正应力修正项（1+σm/σf′）更改为（1+σn，max/σf′）。事实上，基于莫尔圆求解临界面的过程也已经考虑到了多轴及非比例效应对疲劳寿命的影响。另外在计算过程中发现，仅用（1+σn，max/σf′）对剪应变能进行修正，使得预测寿命偏长，因此本多轴模型在剪应变能部分引入了参数P。P可通过材料的单轴扭转试验直接获得，数值在1.0～1.5之间，并未给模型增加未知量。多轴疲劳寿命模型的最终形式为：

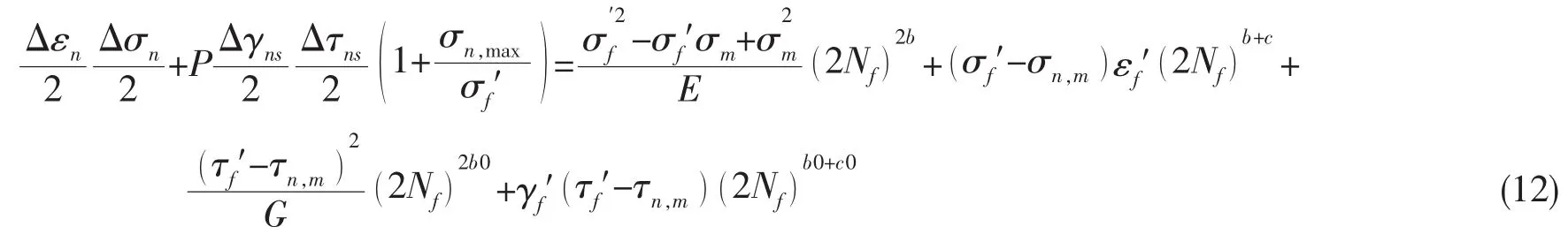
2 数据对比及分析

通过文献[18-20]中的试验数据及材料参数，运用新模型对多种材料在各种载荷下的疲劳寿命进行的预测，表1为本研究所用到的材料的性能参数。计算结果通过Python编程计算获得，计算中对于复杂的载荷采用雨流计数法，应力—应变模型为Miner-Palmgren线性模型。

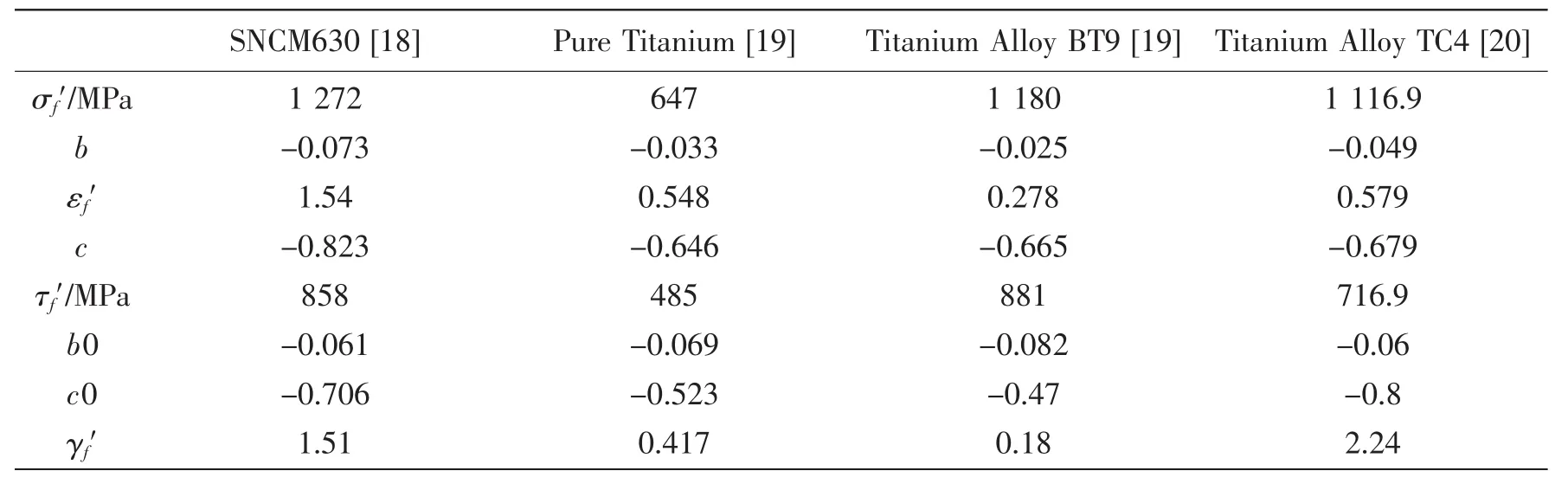
表1 材料属性Tab.1 Fatigue properties of materials used in this study

（1）文献[18]中将SWT模型、Chen模型、FS模型、VF模型的预测结果和SNCM630的试验结果进行了对比。SWT模型对单轴拉压载荷预测结果很好，但是对多轴载荷的预测结果和试验数据一致性差，很多点都落在了5倍的公差带以外。Chen模型对单轴扭转载荷的结果与试验结果一致性很好，但是对于其它载荷下预测寿命都偏长，这主要是由于该模型没有充分考虑平均应力及多轴效应导致的。FS模型和VF模型在低周范围内预测结果都与试验数据一致性很好，在高周范围内有一定的偏差，有部分点甚至落在了三倍的公差带以外，但大多数点都落在了两倍的公差带以内。新模型的预测结果基本都落在了两倍的公差带以内。

（2）对于材料Pure Titanium和Titanium Alloy BT9，文献[19]运用Von Mises等效应变模型和FS模型分别对两种材料的疲劳寿命进行了预测。Von Mises等效应变模型的预测寿命基本能够落在三倍的公差带以内，FS模型的预测结果基本落在两倍的公差带内。新模型的预测数据全部都落在试验数据两倍的公差带以内。

（3）文献[20]中将KBM模型和FS模型的预测结果和Titanium Alloy TC4的试验结果进行对比。两个模型在低周范围内基本都落在了两倍的公差带以内，但是高周范围内很多点与试验结果偏差较大，有部分点甚至落在了三倍的公差带以外。本研究提出的新模型的预测结果全部都落在两倍的公差带以内。

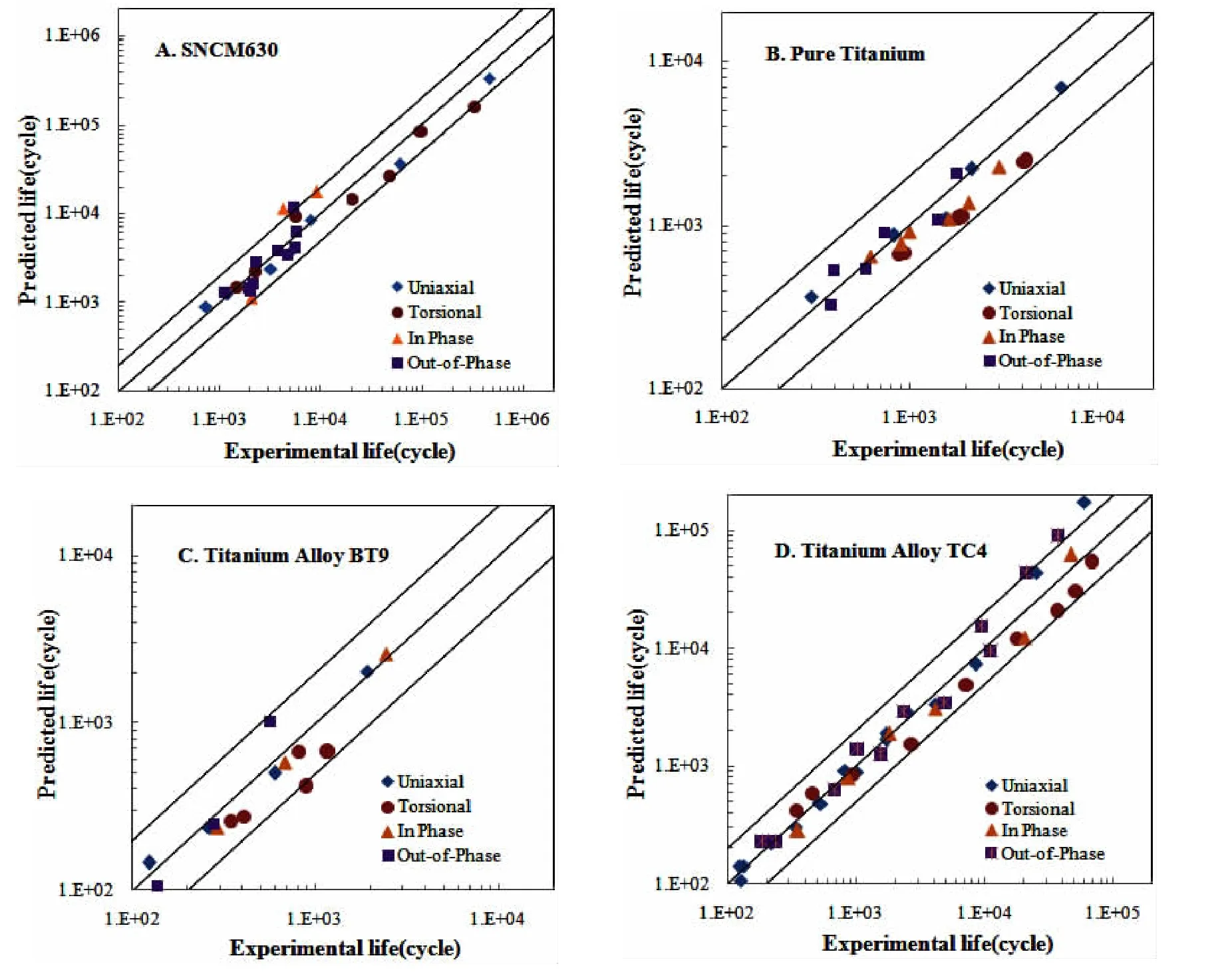
图2 新模型预测寿命和寿命试验值的对比Fig.2 Comparison of consistency between predicted and observed data based all kinds of loading

3 结论

（1）本研究通过求解莫尔圆，将剪应变幅作为确定临界面参数，将临界面上的总应变能作为损伤参量。新模型不仅分别对正应变能和剪应变能部分做出了修正，还引入一个新的修正系数（1+σn，max/σf′）来体现多轴非比例效应。

（2）新模型不但提出了新的损伤参量，还给出了具体的疲劳寿命表达式。将多种材料在各种不同载荷形式下的预测寿命和试验结果对比，虽然材料类型不同，载荷形式不同，但是几乎所有的预测寿命都落在了试验寿命两倍的公差带以内，这证明了新模型的准确性和广泛适用性。

[1]Smith K N,Topper T H,Watson P.A stress-strain function for the fatigue of metals(stress-strain function for metal fatigue including mean stress effect)[J].Journal of Materials,1970,5:767-778.

[2]Glinka G,Shen G,Plumtree A.A multiaxial fatigue strain energy density parameter related to the critical fracture plane [J].Fatigue&Fracture of Engineering Materials&Structures,1995,18(1):37-46.

[3]Glinka G,Wang G,Plumtree A.Mean stress effects in multiaxial fatigue[J].Fatigue&Fracture of Engineering Materials &Structures,1995,18(7-8):755-764.

[4]Chen X,Xu S,Huang D.A critical plane‐strain energy density criterion for multiaxial low-cycle fatigue life under nonproportional loading[J].Fatigue&Fracture of Engineering Materials&Structures,1999,22(8):679-686.

[5]Fatemi A,Socie D F.A critical plane approach to multiaxial fatigue damage including out-of-phase loading[J].Fatigue& Fracture of Engineering Materials&Structures,1988,11(3):149-165.

[6]Varvani-Farahani A.A new energy-critical plane parameter for fatigue life assessment of various metallic materials subjected to in-phase and out-of-phase multiaxial fatigue loading conditions[J].International Journal of Fatigue,2000,22(4): 295-305.

[7]吴志荣,胡绪腾,宋迎东.基于最大切应变幅和修正SWT参数的多轴疲劳寿命预测模型[J].机械工程学报,2013,49 (2):59-66. Wu Z,Hu X,Song Y.Multi-axial fatigue life prediction model based on maximum shear strain amplitude and modified SWT parameter[J].Chinese Journal of Mechanical Engineering,2013,49(2):59-66.

[8]Shang D G,Wang D J.A new multiaxial fatigue damage model based on the critical plane approach[J].International Journal of Fatigue,1998,20(3):241-245.

[9]Li J,Zhang Z,Sun Q,et al.Multiaxial fatigue life prediction for various metallic materials based on the critical plane approach[J].International Journal of Fatigue,2011,33(2):90-101.

[10]SINES G.The prediction of fatigue fracture under combined stresses at stress concentrations[J].Bulletin of JSME,1961,4 (15):443-453.

[11]Sun N N,Chiang Y J,Li G X,et al.A comparative study of fatigue criteria for engineering application[J].Applied Mechanics and Materials,2014,538:356-359.(in Press)

[12]Bergmann J,Klee S,Seeger T.Effect of mean strain and mean stress on the cyclic stress-strain and fracture behavior of steelStE70[J].Material Pruefung,1977,19:10-7.

[13]Papadopoulos I V,Davoli P,Gorla C,et al.A comparative study of multiaxial high-cycle fatigue criteria for metals[J].International Journal of Fatigue,1997:219-235.

[14]Dang Van K,Maitournam H.A unified approach for high and low cycle fatigue based on shakedown concepts[J].Fatigue of Engineering Materials and Structures,2003:561-568.

[15]Liu K C.A method based on virtual strain-energy parameters for multiaxial fatigue life prediction[J].ASTM Special Technical Publication,1993,1191:67-67.

[16]McClaflin D,Fatemi A.Torsional deformation and fatigue of hardened steel including mean stress and stress gradient effect[J]s.International Journal of Fatigue,2004,26(7):773-784.

[17]Socie D F,Marquis G B.Multiaxial fatigue[M].Warrendale,PA:Society of Automotive Engineers,2000.

[18]Han C,Chen X,Kim K S.Evaluation of multiaxial fatigue criteria under irregular loading[J].International Journal of Fatigue,2002,24(9):913-922.

[19]Shamsaei N,Gladskyi M,Panasovskyi K,et al.Multiaxial fatigue of titanium including step loading and load path alteration and sequence effect[J].International Journal of Fatigue,2010,32(11):1862-1874.

[20]Wu Z R,Hu X T,Song Y D.Multiaxial fatigue life prediction for titanium alloy TC4 under proportional and nonproportional loading[J].International Journal of Fatigue,2014,59:170-175.

Study on multiaxial fatigue criterion based on total strain energy

SUN Nan-nan1,LI Guo-xiang1,BAI Shu-zhan1,WANG Yang2,WEI Tao2
(1 School of Energy&Power Engineering,Shandong University,Jinan 250061,China; 2 R&D Center,Weichai Power Co.,Ltd,Weifang 261205,China)

A new multi-axial model fatigue criterion is proposed.Taking into account the advantage and shortage of several existing multi-axial fatigue criteria,modifications are made on the normal energy and shear energy part,and a new multiaxial fatigue criterion is proposed to predict fatigue life under proportional and non-proportional loadings.Through the calculation of Mohr’s circle,shear strain amplitude is taken as the parameter to determine the critical plane and total strain energy is taken as the damage parameter of the new model.The model is evaluated by the multiaxial fatigue test data of SNCM630 steel,pure titanium,titanium alloy BT9,and titanium alloy TC4.Although loadings are complex and various,the predicted data are almost within a factor of 2 scatter band of the test results.The results show that the new model has a higher predicted accuracy.

multi-axial fatigue;energy criterion;critical plane; proportional and non-proportional loading

TK4TG1

A

10.3969/j.issn.1007-7294.2015.04.008

1007-7294（2015）04-0405-06

2014-09-06

国家高科技研究发展计划资助863项目（2014AA041501）

孙楠楠（1985-），女，博士研究生，E-mail:sunnan1020@163.com；

李国祥（1965-），男，教授，博士生导师，E-mail:liguox@sud.edu.cn。