深水张力腿平台非线性涡激特性及水动力性能研究

谷家扬，陶延武，杨建民，肖龙飞

（1江苏科技大学船舶与海洋工程学院，江苏镇江212003；2上海交通大学海洋工程国家重点实验室，上海200240）

深水张力腿平台非线性涡激特性及水动力性能研究

谷家扬1，陶延武1，杨建民2，肖龙飞2

（1江苏科技大学船舶与海洋工程学院，江苏镇江212003；2上海交通大学海洋工程国家重点实验室，上海200240）

平台涡激运动易导致立管及系泊系统疲劳损伤，危害其安全稳定性。该文引入雷诺平均法求解NS方程结合DES湍流模型对不同流速下深水张力腿平台三维涡激运动及流场特性进行了数值研究。采用GAMBIT软件建立计算网格，将求解动力学控制方程的代码嵌入UDF求解器中，采用动网格技术实现流场更新并求得作用于平台立柱和浮箱上的瞬时升力和拖曳力。采用最大值统计法和均方根统计法进行数据统计。研究发现：张力腿平台涡激运动流向振幅的大小随着约化速度的增大而增大，但在小范围内波动；横向振幅曲线最大值出现在0°来流、约化速度U*=8.0处，大小为0.38D；三种来流工况流向平衡位置随无因次速度的增大而增大，但增长速度有所区别，22.5°和45°下流向平衡位置的增加速度要明显大于0°来流；22.5°来流升力系数谱能量较为分散，立柱及浮箱之间的干扰具有强非线性效应；最后对张力腿平台表面压力系数分布及涡量等值面特性进行了分析和探讨。

涡激运动；张力腿平台；动网格；UDF

0 引言

能源需求的不断增长促进了海洋工程的蓬勃发展，张力腿平台作为深海油气开采的一种重要浮式生产平台，必将成为我国南海油气开发战略过程中的重要工具之一。目前张力腿平台主要集中在墨西哥湾、北海以及西非海域，相关技术被欧美国家所垄断。国内的上海交通大学、天津大学、中国海洋石油研究中心、中国船舶科学研究中心及中科研力学所等单位对张力腿平台水动力性能开展了研究和技术论证，为我国设计、建造张力腿平台积累了一定经验。

张力腿平台复杂绕流特性及水动力性能预报是其涡激运功研究的基础，但相关研究较少，多立柱绕流可提供有益参考和借鉴。Lam等[1]2007年对阵列圆柱绕流特性进行了二维、三维数值模拟及实验研究，研究发现雷诺数Re和立柱间距比对尾涡结构有较大的影响，立柱间距比1.5时，数值模拟和试验研究中尾流均表现出明显的双稳态特性，当间距比L/D≥2.5时，流场具有一定对称性，L/D小于3.5且临界雷诺数时，上游尾涡结构受到明显挤压变形。Zou Lin等[2]2008年采用3D LES（large-eddy simulation）湍流模型直接求解NS方程对临界Re数等于1.5×104，间距比分别为1.5和3.5的阵列多圆柱绕流进行了数值模拟和实验研究。Yalpaniyan等[3]2010年采用VOF（Volume of Fluid algorithm）法对张力腿平台在层流及湍流下的二维及三维自由表面流动进行了数值计算，研究发现，上游立柱尾涡明显影响下游立柱的流态，导致上游立柱的尾涡强度大于下游立柱，流速对平台周围波面升高有着很大影响。Abrishamchi等[4]2012年分别采用LES和URANS（Unsteady Reynolds Averaged Navier-Stokes）对张力腿平台水动力荷载进行了三维数值计算，自由液面采用VOF法进行模拟，张力腿平台圆形立柱直径为9.0 m，给出了0°及45°流向下张力腿平台上游及下游立柱升力系数及拖曳力系数的时历和频域曲线。

单个弹性支撑圆柱涡激运动研究由美国Willamson教授及其团队[5-6]开创，其对多立柱平台涡激运动有着重要启发和指导作用。Willamson根据质量-无因次阻尼联合参数m*ξ的高低和振幅形状对不同分支进行了定义，同时对质量比分别为2.6和7.0的弹性支撑圆柱的振幅幅值开展了研究。在Williamson研究基础上，国内学者继续对弹性支撑单柱体及多柱体开展了相关研究。黄智勇[7]、潘志远[8]等对比了不同质量比弹性支撑圆柱在限制流向及不限制流向下的涡激运动特性。梁亮文、万德成等[9]对均匀流中圆柱的受迫振荡进行了数值模拟，研究了圆柱振幅和频率对圆柱受力及尾涡结构的影响，讨论了在锁定及非锁定状态下升力、拖曳力曲线及涡泄结构。郑德乾、顾明等[10]采用并行计算方法对雷诺数为200的方柱涡激运动进行了数值计算，观察到了“拍”和“锁定”现象。

近年来，多柱体涡激运动逐渐引起学术界的关注，研究热点聚焦于不同的排列方式（串列、并列及阵列）及间距比对涡激特性的影响[11-12]。徐枫、欧进萍等[13]对间距比为1.5～6.0正三角形排列的圆柱涡激运动进行了数值模拟，对气动力响应、频率特性及其下游涡泄结构进行了计算。Zhao Ming等[14]2012年采用雷诺平均法求解NS方程结合SST k-ω湍流模型对为0°、15°、30°和45°流向，间距比等于3，约化速度1～20阵列多圆柱二维涡激运动进行了数值模拟。研究发现：流向对涡激运动幅值及锁定区间影响很大，不过，研究中质量比设为2.0，远大于张力腿平台的质量比，较难反映出张力腿平台涡激运动特性。

目前海洋工程中涡激运动研究最多、最深刻的是单立柱平台，上海交通大学的杨建民教授[15]、天津大学的唐友刚教授[16-17]、大连理工大学的宗智教授[18]对Spar平台涡激运动开展了相关研究。张力腿平台作为一种多立柱顺应式平台，各立柱之间存在着相互耦合作用，注定其涡激运动显示出与Spar平台、细长立管、海底管线截然不同的特性。一方面，张力腿平台极低的质量比（由于张力腿巨大预张力，其平台质量比一般只有0.6～0.8，而半潜平台和Spar平台质量比均接近1.0）导致其涡激运动产生更大的横向幅值；另一方面由于浮箱的存在、上下游多立柱流场之间的影响、作为顺应式平台独特的系泊方式及水动力特性等决定了其涡激运动现象更为复杂。

张力腿平台涡激运动数值模拟主要借助商业软件如Fluent、CFX等，但由于计算资源的制约，当前研究停滞于二维仿真阶段，三维数值模拟研究鲜有报道。Kim等[19]2011年分别采用AcuSolve及STAR-CCM+软件对立柱直径为12.8 m的张力腿平台涡激运动进行了数值模拟。针对45°流向，约化速度分别为8.0、9.5和11.2时的涡激运动进行了计算，考虑纵荡、横荡及首摇三自由度之间的耦合，并将数值模拟结果与试验值进行了对比。但不足之处在于，研究中仅计及一个流向和三个约化速度，难以全面归纳张力腿平台涡激运动规律。

近年来，国外学者在拖曳水池中进行了张力腿平台涡激运动试验研究。Leverette等[20]2003年对工作于墨西哥湾的两座SeaStar型张力腿平台，Allegeny和Typhoon在漩涡流下的涡激运动进行了研究。Waals等[21]2007年选取4浮箱深吃水半潜平台（质量比0.83）、4浮箱深吃水张力腿平台（质量比0.57）、4浮箱经典半潜平台（质量比0.84）、2浮箱典型半潜平台（质量比0.83）对其涡激运动进行了试验研究，旨在探讨质量比、激励长度、浮箱、流速及流向对涡激运动的影响。Rijen等[22]2008年通过模型试验研究了流及微幅波联合作用下四立柱半潜平台涡激运动的影响。Hong等[23]2008年研究了波浪对深吃水半潜平台涡激运动影响，试验结果表明：半潜平台发生涡激运动时，横荡运动响应较明显，横荡幅值不仅取决于流速，还与波浪有关，在强流环境中，波浪越小，运动幅值越大。Jimmy Ng等[24]2010年对仅考虑波、流以及波流联合作用下多立柱平台进行试验研究，研究了上游立柱尾流对下游立柱的影响及下游立柱的动力特性。Magee等[25]2011年对一座由Shell及Technip公司共同投资的工作于东南亚海域的张力腿平台涡激运动进行了试验，图1为该平台在某拖曳水池中的试验图片，图2为试验相关装置的原理图。

图1 张力腿平台模型试验图Fig.1 TLP model in configuration

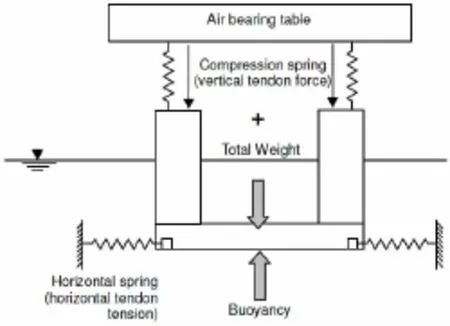
图2 张力腿平台模型试验中采用的倒置压缩弹簧原理图Fig.2 TLP model test with inverted compression spring system set-up in available water depth

张力腿平台涡激运动机理是非常复杂的流固耦合问题，涉及到外部粘性边界层的模拟、耦合运动方程的求解、UDF程序的开发、动网格技术的应用、边界条件的设置等。当前，数值模拟研究受到计算资源的制约，停滞于二维仿真阶段，三维数值模拟研究较少。模型试验研究均在拖曳水池中进行，忽略了张力腿平台特殊的系泊方式，部分模型试验平台质量比与实际相差较大，试验结果难以使人信服。本文对同一流向不同流速下深水张力腿平台三维涡激运动进行了研究，对涡激运动流向平衡位置、流向及横向涡激运动振幅进行了统计，并对平台表面压力系数及涡量等直面进行了分析。

1 数值计算模型

1.1 控制方程

1.1.1 计算流体力学控制方程

不可压缩粘性流体的控制方程为质量和动量守恒方程：

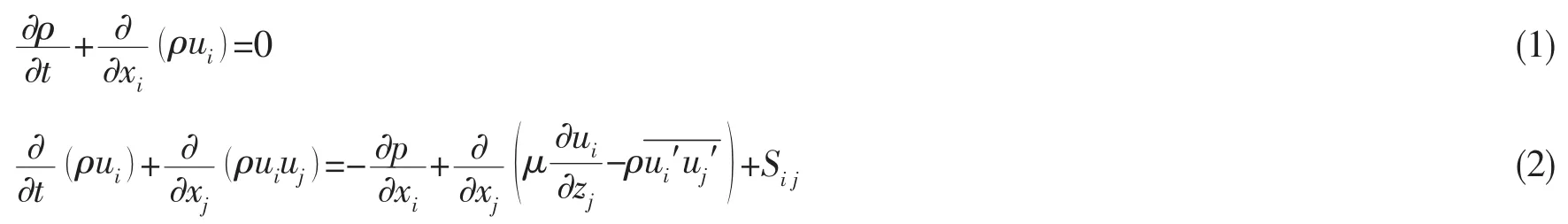
方程（1），（2）均为张量形式，其中x为直角坐标系下的位置，u为速度分量，i，j∈（1，2，3），ρ、t和p代表密度，时间和压力。μ为粘性系数，本文所取流体密度ρ=998.2 kg/m3，运动粘性系数υ=1.0×10-6m2/s，Sij为应变率张量，

鉴于大涡数值模拟适用于高雷诺数下湍流流动，对近壁面小尺度涡处理上有一定的局限性，本文采用DES（Detached Eddy Simulation）湍流模型。其基本处理思想是对近壁区边界层采用统计模型方法（RANS），对分离区采用LES（Large Eddy Simulation）进行数值模拟。分离涡模拟法过程中采用了统一的涡粘输运方程（Spalart-Allmaras涡粘模型），通过网格分辨尺度区分RANS和LES。

1.1.2 无因次动力学控制方程

张力腿平台涡激运动特性主要由如下参数决定：雷诺数Re、斯特罗哈数St、质量比m*、阻尼因子ξ、约化速度Ur、固有频率fn、外部海洋环境、平台主体表面粗糙度、附属结构物、系泊系统和立管的阻尼、平台激励长度、来流湍流强度等。

本文研究限制及不限制流向下张力腿平台的涡激运动问题，将平台简化成弹性支承体，不限制流向时平台无因次动力学方程为：

1.2 计算模型

以南海实际海流速度分布为背景，对张力腿平台在不同来流速度下的涡激运动及流场特性模拟。图3为张力腿平台立柱和浮箱示意图，其中L为两立柱间间距，U为来流速度，θ为来流角度，分别为0°、22.5°和45°，立柱依次标号分别为C1，C2，C3，C4，浮箱依次标号分别为P1，P2，P3，P4。

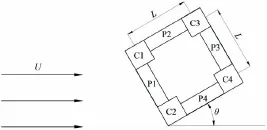
图3 张力腿平台二维布置简图Fig.3 A general 2-D configuration of the TLP

张力腿平台三维涡激运动数值模型采用1:40的缩尺比，方柱边长为0.435 m（D），张力腿平台近壁区域，需对其进行特别处理，以避免高扭曲度单元所带来的计算问题，保证网格的高质量性。计算模型均采用40D×20D×6D长方体流场区域，模型左侧采用速度入口边界条件，右侧采用出流边界条件，其它均为对称边界条件，张力腿平台表面采用无滑移壁面边界条件。划分网格时将整个流场区域划分为多个区域，以控制网格质量及网格数目。张力腿平台壁面附近采用精细的网格控制网格质量，保证数值模拟的精确性，并使第一层网格布置于粘性对数层内，以满足复杂边界条件。为提高计算的精度，张力腿平台周围及尾流区域采用较密网格；为提高计算效率，其它区域采用的是较疏的网格，第一层网格y+范围为[30，100]。在三维涡激运动研究中，考虑到平台运动对周围网格的拉伸和压缩，引起网格变形破坏产生负体积，从而导致计算终止，因此在动网格计算过程中在平台立柱周围设置了0.6D大小的随体区域。

计算流场域采用Fluent分离求解器进行求解，采用DES湍流模型和非稳态一阶隐式进行求解，动量方程的压力速度耦合采用SIMPLEC算法，动量、湍流动能和耗散率项均采用Bounded Central Differencing格式。计算采用CPU为I7-2600@3.40 GHz，内存为8G的计算机，计算时间间隔为0.05 s，共计算600 s，每个约化速度算例计算耗时约50天。数据处理中选取较为稳定的100～600 s进行统计。

图4 三维张力腿平台数值网格划分Fig.4 3D numerical meshes of TLP

2 计算结果与分析

2.1 流向及横向涡激运动特性

三维涡激运动研究中，考虑了三种典型的来流方向，即0°、22.5°和45°。每种来流方向下选取约化速度的范围为2.0-12.0，约化速度间隔△U*=1.0。图5、图6和图7分别给出了0°来流、22.5°来流和45°来流下，平台在不同约化速度下流向和横向涡激运动无因次位移时间历程曲线。从图中可以看出，流向和横向位移曲线并没有单柱体涡激运动位移时历曲线那么规则，这不仅与多柱体及浮箱之间的流动分离与剪切层干扰效应的复杂性有关，还与结构所受流体力及相关频率特性具有强烈的非线性特性相关。流向和横向位移曲线在约化速度比较小时的周期性和规则性要比约化速度比较大时的强，这主要是来流速较大时，漩涡能充分的形成，体现出漩涡的三维随机性和脉动性。来流方向对平台涡激运动响应有很大的影响，平台在相同的约化速度下的流向和横向位移时历曲线相差很大。平台在平均拖曳力的作用下在流向偏移到一个新平衡位置，由于脉动拖曳力的作用，平台在流向平衡位置处做往复运动，平台在流向往复运动的周期与脉动拖曳力紧密相关，因此流向平衡位置随无因次流速的变化趋势和规律是涡激运动研究中关注的重要问题。

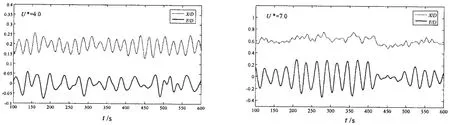
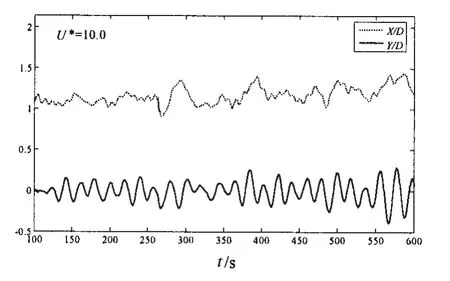
图5 不同约化速度下流向及横向涡激运动位移时间历程曲线，0°来流Fig.5 Time histories of stream-wise and transverse displacement with different reduced velocities from 0 degree flow

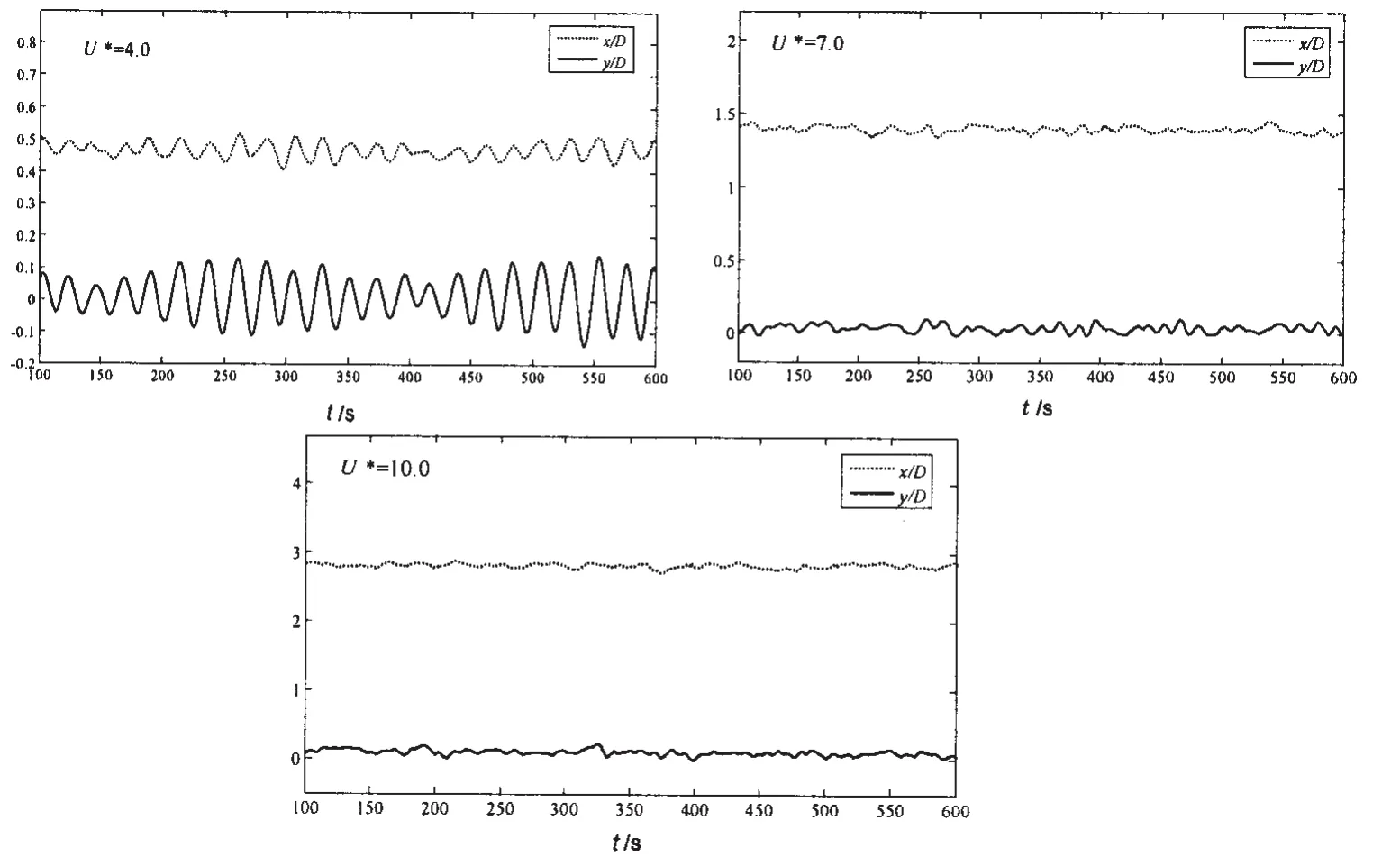
图6 不同约化速度下流向及横向涡激运动位移时间历程曲线，22.5°来流Fig.6 Time histories of stream-wise and transverse displacement with different reduced velocities from 22.5 degrees flow

图7 不同约化速度下流向及横向涡激运动位移时间历程曲线，45°来流Fig.7 Time histories of stream-wise and transverse displacement with different reduced velocities from 45 degrees flow

图8给出了0°、22.5°和45°和这三种典型来流角度下，平台在不同约化速度下流向平衡位置远离初始位置的距离。三种来流角度下流向平衡位置均随着约化速度增大而不断增大，但增长的速度不同，22.5°来流和45°来流流向平衡位置的增加速度要明显大于0°来流工况。0°来流下的流向平衡位置随约化速度的增大基本上是线性增加。在相同的约化速度下45°来流工况下的流向平衡位置要大于其他两种工况，当约化速度达到12.0时，0°来流、22.5°来流和45°来流的流向平衡位置分别为1.60D、4.06D和5.10D，45°来流的流向平衡位置此时为0°来流的3.19倍，这足以说明来流方向对平台流向平衡位置的影响很大。

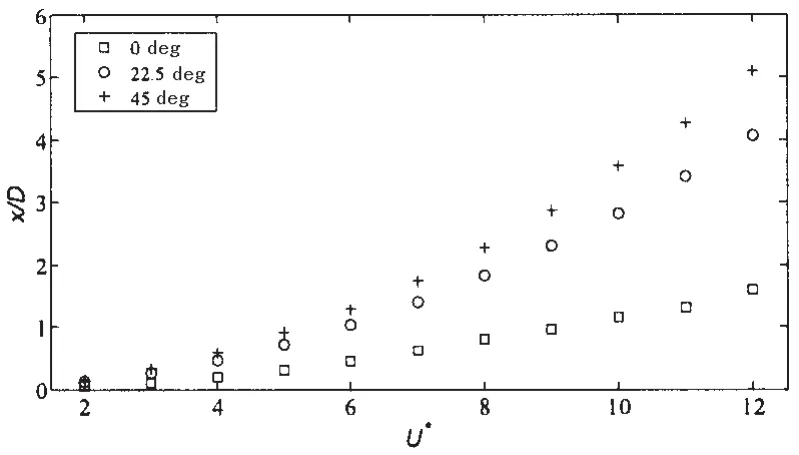
图8 流向平衡位置随约化速度变化趋势图Fig.8 Equilibrium position of stream-wise amplitude at different reduced velocities

研究平台涡激运动的特性，其中运动幅值是考察的一个重要数据，既要关注运动幅值的最大值，又要关注幅值的标称值，因此本文采用两种统计方法对振幅进行统计，一种为最大振幅统计法，另一种为标称振幅统计法，具体公式如下：

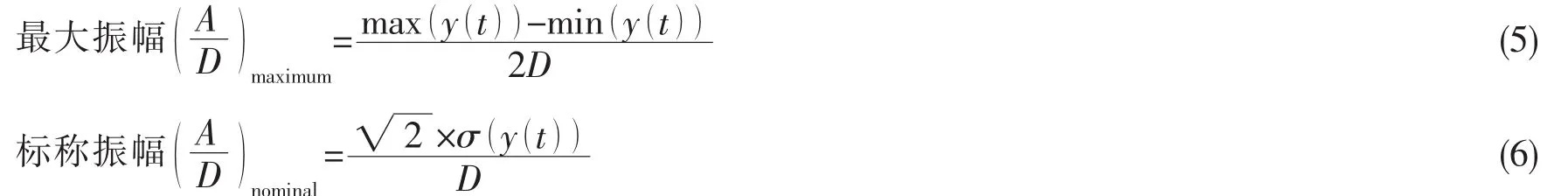
式中：max（y（t））为最大位移，min（y（t））为最小位移，σ（y（t））为位移标准差。

总而言之，机械电气设备受安装及运行环境影响，故障种类及应急处理措施具有极大的差异性，需相关维修人员注重对机械电气设备诊断技术的不断完善及优化，及时判断并记录下机械电气设备故障发生的症结所在，并为后续故障处理工作提供有力的数据支持，以将机械电气设备故障所造成的经济损失控制在最低范围之内。

图9和图10分别为采用两种统计方法得到的流向涡激运动幅值随无因次约化速度的变化规律曲线。从两张图的整体走势来看，采用两种统计方法得到的规律基本接近，但在幅值大小上存在着一定差距，采用最大统计法得到的振幅幅值在流向和横向均大于标称统计法得到的结果。总体而言，流向振幅的大小随着约化速度的增大而增大，但在小范围内波动。在相同的约化速度下，0°来流下的振幅总体上大于其它两种来流工况下的振幅，其中22.5°来流工况下的流向振幅最小。0°来流、22.5°来流和45°来流工况的流向振幅均在约化速度U*=12.0时达到最大值，大小依次为0.34D、0.09D和0.20D，以此可以看出来流方向对流向振幅的影响很大。平台涡激运动流向振幅响应结果和单柱体涡激运动流向振幅结果明显不同，没有出现单柱体涡激运动流向振幅随约化速度的增加先上升后下降的趋势，这与多柱体和浮箱之间的耦合作用相关。

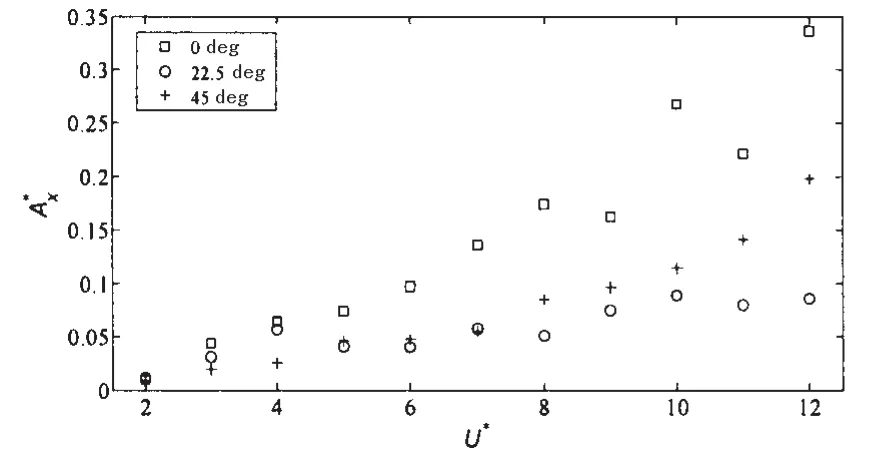
图9 不同约化速度下流向振幅A曲线（最大振幅统计法）Fig.9 Stream-wise amplitude at different reduced velocities(maximum response)

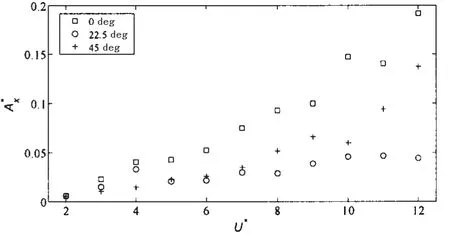
图10 不同约化速度下流向振幅A曲线（标称振幅统计法）Fig.10 Stream-wise amplitude at different reduced velocities(nominal response)

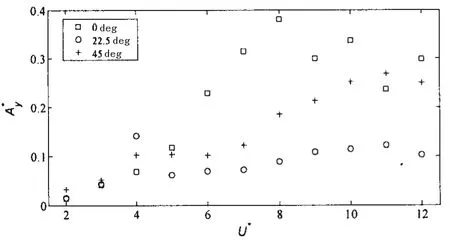
图11 不同约化速度下横向振幅A曲线（最大振幅统计法）Fig.11 Transverse amplitude at different reduced velocities(maximum response)

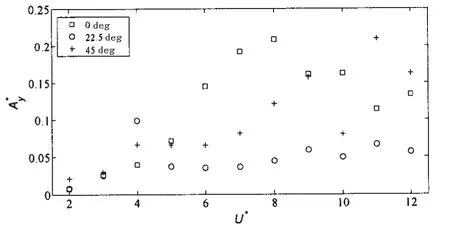
图12 不同约化速度下横向振幅A曲线（标称振幅统计法）Fig.12 Transverse amplitude at different reduced velocities(nominal response)

图11和图12分别给出了两种不同统计方法下平台横向振幅随约化速度的变化规律。两种不同统计法下横向振幅随约化速度的总体变化规律相类似，但45°来流工况在高约化速度下的变化趋势略有不同。从图11可以看出，0°来流工况横向振幅曲线在约化速度U*=8.0处出现了最大值，大小为0.38D，随后随着约化速度的增加有下降的趋势，这与单圆柱涡激运动初始激励分支和下端分支相类似，但是没有出现幅值跳跃的现象。然而22.5°来流工况和45°工况与0°工况不同，横向振幅均在约化速度U*=11.0达到最大值0.12D和0.27D，随后横向振幅曲线有下降趋势。从图9-12可以看出，0°来流下平台涡激运动响应要比其他两种工况要大，22.5°来流工况最小。对比文献[25]中的试验结果，试验数据的处理方法是采用最大值统计法进行统计，试验中张力腿平台的质量比为0.83，与本文张力腿平台的质量比0.78基本接近，两者均为方形立柱。从振幅曲线随约化速度的变化趋势上来看，与本文0°来流振幅变化趋势基本吻合，由于质量比和平台主尺度的影响（试验中平台为非对称结构，而本文研究的TLP为对称结构），最大幅值出现处的约化速度有所区别，试验中0°来流横向最大幅值出现在U*= 10.0，最大值约为0.46D，大于本文的0.38D。试验中约化速度10～20范围内横向振幅基本锁定在0.4D附近。从上述数值模拟与试验结果的对比来看，横向振幅变化趋势基本与试验数据吻合，一定程度上说明本文模型网格划分的精确性、可靠性以及流固耦合程序编制的正确性。

2.2 升力系数时历曲线及谱分析

图13-15给出了不同约化速度下张力腿平台涡激运动升力系数的时间历程曲线及频谱变换图，为了节约篇幅，论文仅给出不同来流角度下四个典型约化速度，分别为3.0、5.0、7.0和10.0。快速傅里叶变换可以将数值模拟得出的升力系数相对时间的函数得出系统能量在不同频率上的密度分布，从而将时域计算结果转到频域上面来分析。从涡激运动原理可知，平台横向涡激运动的变化规律、周期大小以及振幅幅值都与升力系数密切相关，受力决定运动。笔者截取了100-600 s范围内的稳定阶段，0°来流工况升力系数时历曲线图出现了锯齿状，但其谱密度相对比较集中，如图13（b-c）所示。22.5°来流工况谱分析结果和0°来流工况明显不同，在约化速度比较小时，如图14（a），系统能量比较集中，随着约化速度的增大，系统能量的极值不止一个，甚至出现很多个，即系统处于多频响应模式，如图14（b-d）所示。这说明结构所受流体力及频率特性具有强烈的非线性特性，立柱及浮箱之间的相互干扰最强。45°来流工况下升力系数的简谐性没有其它两种工况好，升力系数曲线变化比较大，对比其相对应的频谱图可以看出，系统的能量主要集中在低频，即系统处于超低频响应模式。

图13 不同约化速度下张力腿平台升力系数时历曲线及其频域分析，0°来流Fig.13 Time histories of lift coefficient at different reduced velocities and FFT analysis from 0 degree current

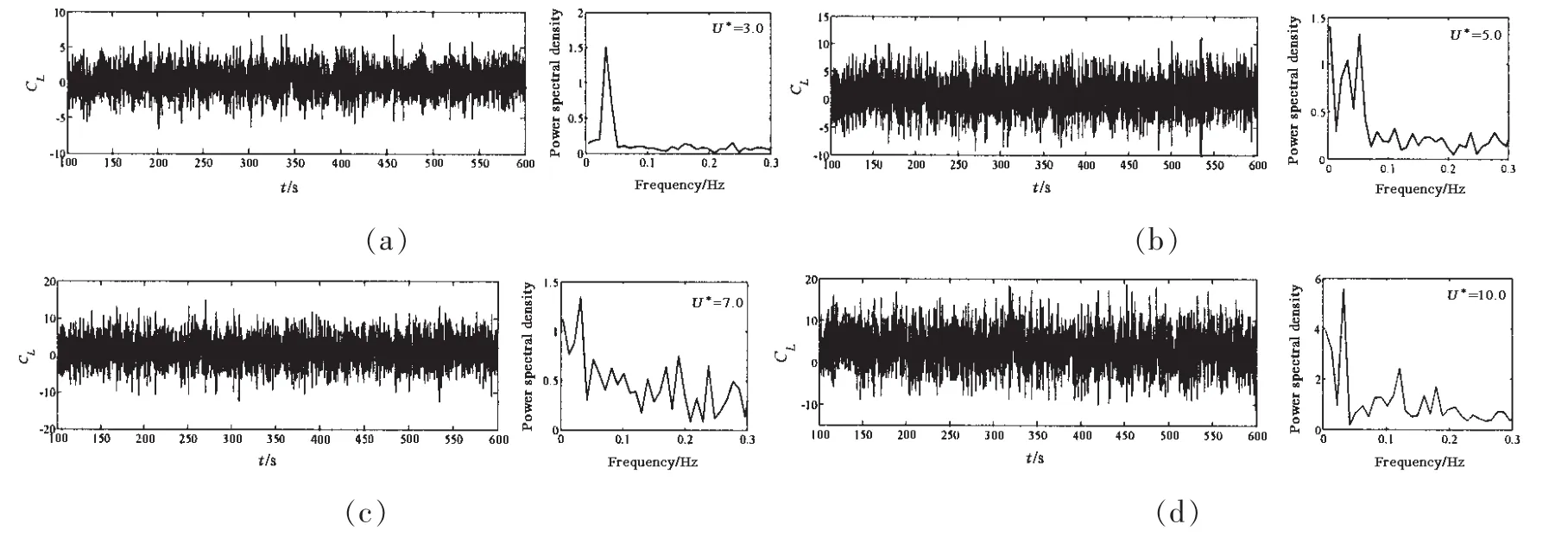
图14 不同约化速度下张力腿平台升力系数时历曲线及其频域分析，22.5°来流Fig.14 Time histories of lift coefficient at different reduced velocities and FFT analysis from 22.5 degrees current

图15 不同约化速度下张力腿平台升力系数时历曲线及其频域分析，45°来流Fig.15 Time histories of lift coefficient at different reduced velocities and FFT analysis from 45 degrees current

2.3 张力腿平台表面压力系数分布研究

图16为某一时刻不同约化速度下张力腿平台表面压力系数分布图，该图体现了张力腿平台涡激运动下三维受力情况，间接体现了不同约化速度下张力腿平台流向与横向的运动特点。较低约化速度下，上游立柱及浮箱所受流向力较大，流体绕过上游立柱及浮箱后，流体力减弱，作用到下游立柱及浮箱时，流向力已大幅削弱。由于流体流经平台时流动分离，出现了负压力梯度，促使漩涡生成，下游立柱处于上游立柱尾涡区内，并与下游柱体的尾涡合并产生尺度不同、秩序更加凌乱的涡，进而又影响下游立柱的压力分布。当约化速度比较高时，漩涡充分生成，如22.5°来流和45°来流约化速度为9.0工况，平台表面的负压力梯度区域更大。平台表面压力系数分布的不均匀且随时间不停的变化，促使平台更加不规则的运动，很好的解释了平台时历曲线的不规则性。

图16 某一时刻不同约化速度下张力腿平台表面压力系数分布图Fig.16 Pressure coefficient distribution contours on the surface of TLP at different reduced velocities and at some time

2.4 张力腿平台涡量等值面特性

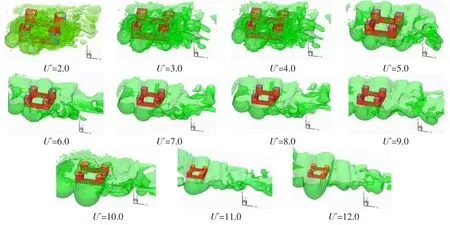
图17 不同约化速度下涡量等值面图Fig.17 Vorticity ISO surfaces of TLP at different reduced velocities

3 结语

本文介绍了当前国际上多立柱平台的试验研究方法和数值模拟方法，研究了0°流向、22.5°流向和45°流向下平台的涡激运动特性，对平台流向和横向涡激运动幅值随无因次速度的变化趋势、流向平衡位置、引起横向涡激运动升力系数的时间历程曲线和频率特性进行了探讨并得出了如下结论：

（1）总体而言，张力腿平台三维涡激运动流向振幅的大小随着约化速度的增大而增大，但在小范围内波动，最大值出现在0°来流工况约化速度U*=12.0处，大小为0.34D。横向振幅曲线最大值出现在0°来流工况约化速度U*=8.0处，大小为0.38D。0°来流工况横向振幅曲线与经典圆柱涡激运动初始激励分支和下端分支相类似，但没有幅值跳跃现象，22.5°来流工况流向振幅和横向振幅最小。

（2）三种来流工况流向平衡位置随无因次速度的增大而增大，但增长的速度不同，22.5°来流和45°来流流向平衡位置的增加速度要明显大于0°来流工况。相同约化速度下，45°来流工况流向平衡位置大于其他两种工况，0°来流工况最小。

（3）22.5°来流工况升力系数谱能量比较分散，立柱及浮箱之间干扰性比较强，具有强烈的非线性。0°来流工况和45°来流工况谱能量相对比较集中。

（4）压力系数分布图体现了张力腿平台在涡激运动时受力分布情况及沿横向、流向的运动情况。在低约化速度下，张力腿平台周围涡破碎较为严重并形成大量块状及筒状涡；而在高约化速度下，涡量等值面较为光滑而又有周期性，形成了上卷形状柱状涡，并于一定范围内出现少量破碎涡。

[1]Lam K,Zou L.Experimental and numerical study for the cross-flow around four cylinders in an In-line square configuration[J].Journal of Mechanical Science and Technology,2007,24(1):1338-1343.

[2]Zou Lin,Lin Yufeng.Large-eddy simulation of flow around cylinder arrays at a subcritical reynolds number[J].Journal of Hydrodynamics,2008,20(4):403-413.

[3]Yalpaniyan A,Goodarzi M.The free surface flow around a TLP[C].Proceedings of the ASME 2010 29th International Conference on Offshore Mechanics and Arctic Engineering,OMAE,2010-20021.

[4]Abrishamachi A,Younis B A.LES and URANS predictions of hydrodynamic loads on a tension-leg platform[J].Journal of Fluids and Structures,2012,28:244-262.

[5]Jauvtis N,Williamson C H K.The effect of two degrees of freedom on vortex-induced vibration at low mass and damping [J].Journal of Fluids Mechanics,2004,509:23-62.

[6]Govardhan R,Williamson C H K.Defining the modified Griffin plot in vortex-induced vibration revealing the effect of Reynolds number using controlled damping[J].Journal of Fluid Mechanics,2006,561(00):147-180.

[7]黄智勇,潘志远,崔维成.两向自由度低质量比圆柱体涡激振动的数值计算[J].船舶力学,2007,11(1):1-9. Huang Zhiyong,Pan Zhiyuan,Cui Weicheng.Numerical simulation of VIV of a circular cylinder with two degrees of freedom and low mass-ratio[J].Journal of Ship Mechanics,2007,11(1):1-9.

[8]潘志远.海洋立管涡激振动机理与预报方法研究[D].上海:上海交通大学,2006. Pan Zhiyuan.Vortex Induced Vibration of marine riser and response prediction[D].Shanghai:Shanghai Jiao Tong University,2006.

[9]梁亮文,万德成.横向受迫振荡圆柱低雷诺数绕流问题数值模拟[J].海洋工程,2009,7(4):45-60. Liang Liangwen,Wan Decheng.Numerical investigation of a forced oscillating cylinder in a cross flows with low Reynolds number[J].The Ocean Engineering,2009,7(4):45-60.

[10]郑德乾,顾明,张爱社.基于流体并行计算的二维方柱涡激振动数值模拟[J].噪声与振动控制,2009,29(6):85-91. Zheng Deqian,Gu ming,Zhang aishe.Numerical simulation of vortex-induced vibration for 2D square cylinder based on parallel computation for fluid domain[J].Noise and Vibration Control,2009,29(6):85-91.

[11]Sumner D.Closely spaced circular cylinders in cross-flow and a universal wake number[J].Journal of Fluids Engineering, 2004,126(2):245-249.

[12]Sumner D,Richards M D,Akosile O O.Two staggered circular cylinders of equal diameter in cross-flow[J].Journal of Fluids and Structures,2005,20(2):55-276.

[13]徐枫,欧进萍.正三角形排列三圆柱绕流与涡致振动数值模拟[J].空气动力学学报,2010,28(5):582-590. Xu Feng,Ou Jinping.Numerical simulation of vortex-induced vibration of three cylinders subjected to a cross flow in equilateral arrangement[J].ACTA AERODYNAMICA SINICA,2010,28(5):582-590.

[14]Zhao Ming,Cheng Liang.Numerical simulation of vortex-induced vibration of four circular cylinders in a square configuration[J].Journal of Fluids and Structures,2012,31:125-140.

[15]王颖.Spar平台涡激运动关键特性研究[D].上海:上海交通大学,2010. Wang Yin.Research on the key characteristics of spar vortex-induced motions[D].Shanghai:Shanghai Jiao Tong University,2010.

[16]沈文君,唐友刚,赵晶瑞.桁架式Spar平台垂荡板结构的水动力特性[J].天津大学学报,2011,44(6):491-496. Shen Wenjun,Tang Yougang,Zhao Jingrui.Hydrodynamic characteristics of heave plate structure for Truss Spar[J].Journal of Tianjin University,2011,44(6):491-496.

[17]沈文君,唐友刚,李红霞.随机波浪下Truss Spar平台垂荡运动时域分析[J].海洋工程,2012,30(1):60-65. Shen Wenjun,Tang Yougang,Li Hongxia.Time domain analysis of heave motion for Truss Spar in random seas[J].The Ocean Engineering,2012,30(1):60-65.

[18]高云,宗智,于馨.Spar平台涡激运动响应分析[J].中国海洋平台,2011,26(1):17-22. Gao Yun,Zong Zhi,Yu Xin.Response analysis of vortex induced Spar motions[J].China Offshore Platform,2011,26(1): 17-22.

[19]Kim Jang-Whan,Magee A,Guan K Y H.CFD simulation of flow-induced motions of a multi-column floating platform[C]. Proceedings of the 30th International Conference on Offshore Mechanics and Arctic Engineering,OMAE,2011-49437.

[20]Lecerette S,Rijken O,Dooley W.Analysis of TLP VIV response to eddy currents[C].Proceedings of Offshore Technology Conference,OTC,2003-15289.

[21]Waals J Olaf J,Bultema S.Flow induced motions of multi column floaters[C].Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering,OMAE,2007-29539.

[22]Rijken O,Leverette S.Experimental study into vortex induced motion response of semi submersibles with square columns [C].Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering,OMAE,2008-57396.

[23]Hong Yongpyo,Cho Yongho,Lee Junyoung,Kim Youngbok.Vortex-induced motion of a deep-draft semi-submersible in current and waves[C].Proceedings of the 18th International Society Offshore and Polar Engineering,ISOPE,2008:453-459.

[24]Jimmy Ng K T,Halkyard J E,Soon C E.Statistical characteristics of flow in the wake region of a vertical bluff cylinder in waves,currents and combined wave-current flows[C].Proceedings of the ASME 2010 29th International Conference on Offshore Mechanics and Arctic Engineering,OMAE,2010-21181.

[25]Magee A,Sheikh R,Guan K Y H.Model tests for VIM of multi-column floating platform[C].Proceedings of the ASME 2011 30th International Conference on Offshore Mechanics and Arctic Engineering,OMAE,2011-49151.

Study on the nonlinear characteristics of vortex induced motion and hydrodynamic performance of deepwater TLP

GU Jia-yang1,TAO Yan-wu1,YANG Jian-min2,XIAO Long-fei2
(1 School of Naval Architecture and Marine Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003, China;2 State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Vortex-induced motions of platforms are associated with rise and mooring system’s fatigue damage,which also endanger its security and stability.This paper studies the 3D vortex-induced motion and the flow field characteristics of deepwater TLP under different current velocities based on RANS(Reynolds-Averaged Navier-Stokes)solver for N-S equation combing with DES(Detached eddy simulation)turbulence model.Computational grid was set up by GAMBIT software and the code of solving dynamic control equations was embedded to UDF(User Defined Function).The instantaneous drag and lift forces of the columns and pontoons can be solved after the flow field renewal is achieved by dynamic mesh technology.The maximum statistical method and nominal statistical method were used to analysis the simulation results.Theresults indicate that the maximum stream-wise amplitude of TLP increase with the increase of reduced velocity,but it fluctuates on a small scale.The maximum transverse amplitude happen at the reduced velocity of 8.0 from 0 degree current,and the value is 0.38D.The stream-wise equilibrium position of three different flow approach angles increase with the increase of reduced velocity,but the growth rate is different. The growth rate of 22.5 degrees current and 45 degrees current cases is lager than the 0 degree current case.Spectrum energy of lift coefficient is relatively decentralized and the interference between column and pontoon has nonlinear effect.Finally,the pressure coefficient distribution and vorticity iso-surface characteristics of TLP surface are discussed.

vortex induced motion;tension leg platform(TLP);dynamic mesh;user defined functions

U357

A

10.3969/j.issn.1007-7294.2015.04.004

1007-7294（2015）04-0369-12

2014-09-25

国家自然科学基金资助项目（51309123，51279104）；江苏省高校自然科学研究资助项目（13KJB570002）；江苏省高校“青蓝工程”资助；江苏高校优势学科建设工程自助项目（PAPD）；江苏省船舶先进设计制造技术重点实验室开放研究基金资助项目（CJ1203）

谷家扬（1979-），男，副教授，E-mail:gujiayang@126.com；陶延武（1990-），男，硕士研究生；

杨建民（1958-），男，教授，博士生导师。