各向异性湍流积分长度数值预报研究
蒋靖伟,马 骋,钱正芳,2,陈 科,蔡昊鹏,张 赫
(1海军装备研究院,北京 100161;2海军工程大学,武汉 430033;3中国舰船研究院,北京100101)
各向异性湍流积分长度数值预报研究
蒋靖伟1,马 骋1,钱正芳1,2,陈 科1,蔡昊鹏1,张 赫3
(1海军装备研究院,北京 100161;2海军工程大学,武汉 430033;3中国舰船研究院,北京100101)
文章针对目前模型试验只能获得各向同性湍流积分长度这一现状,建立了各向异性湍流积分长度数值预报方法:(1)RANS预报初始定常流场;(2)大涡模拟计算脉动速度场;(3)脉动速度相关函数计算各向同性湍流积分长度;(4)计算各向异性湍流积分长度。通过二维水翼模型试验验证了水中各向同性湍流积分长度的数值预报精度,平均误差6.81%;通过风洞螺旋桨验证了空气中各向异性湍流积分长度计算方法。对SUBOFF桨盘面处各向异性湍流积分长度的预报研究发现,各方向湍流积分长度外半径大于内半径;潜艇上部涡团扩散较下部明显,内半径湍流积分长度波峰随着角度增大而内移周向分布受指挥台围壳和稳定翼马蹄涡影响,波峰出现在20°和90°左右的频率峰值受指挥台围壳和稳定翼马蹄涡脱落频率(约15 Hz)影响,峰值集中在30 Hz以下。该文提出的各向异性湍流积分长度预报方法,为下一步螺旋桨低频宽带噪声预报中构造新的湍流波数谱以提高预报精度提出了思路。
各向异性湍流积分长度;数值预报;CFD;大涡模拟
0 引 言
螺旋桨低频宽带噪声的预报是目前潜艇螺旋桨噪声研究的重点和热点[1-8],是潜艇进一步减震降噪需要突破的关键技术。谱方法是目前预报低频宽带噪声的主流方法。谱方法由Blake(1986)[1]提出完整的理论,随后Kirschner(1993)[2]提出条带理论,建立了螺旋桨低频宽带噪声的数值预报方法,其计算流程如图1。

图1 条带理论计算流程Fig.1 Procedure diagram of strip theory
其中作为表征湍流信息的湍流波数谱对螺旋桨低频宽带噪声的精确预报起着重要作用,湍流波数谱由湍流积分长度和湍流度构成,其表达式为(以三维Liepmann谱[3]为例)

目前湍流积分长度的获取主要是通过模型试验[6-8],模型试验主要有以下不足:(1)无论是风洞热线单点测量法还是空泡水筒中PIV试验方法,都是基于各向同性假设,测量的是各向同性湍流积分长度;(2)试验费时费力,加工模型造成额外成本;(3)不同测试系统(风洞、水池、循环水槽等)的试验测量结果对于潜艇艉部各向异性湍流场的适用性并没有进行过系统的研究分析。为弥补试验及目前理论研究中的不足,本文建立了各向异性湍流积分长度的数值预报方法,通过数值计算结果对比二维水翼验证了水槽各向同性湍流积分长度,对比空气中螺旋桨试验数据验证了风洞各向异性湍流积分长度数值预报方法;其次,用建立的数值方法预报了SUBOFF潜艇桨盘面处各向异性湍流积分长度,对不同半径、不同频率的各向异性湍流积分长度进行了研究分析;文章的最后对全文进行了总结展望。
1 各向异性湍流积分长度数值预报方法
各向湍流积分长度的数值预报,分为四个步骤:定常流场预报、脉动流场预报和积分长度计算。(1)在定常流场求解中,本文使用Shear-Stress Transport(SST)k-ω湍流模式来封闭雷诺应力;(2)在脉动流场求解中,考虑到直接数值模拟(Direct Numerical Simulation,DNS)的计算量是目前难以承受的,本文采用大涡模拟(Large Eddy Simulation,LES)方法求解脉动速度场,亚格子模式采用动态湍动能输运(Dynamic Kinetic Energy Transport,DKET);(3)在各向同性积分长度的计算中,通过脉动速度相关函数来计算;(4)在各向异性积分长度的计算中,采用Blake(2002)[9]提出的各向异性湍流积分长度计算公式。
数值预报方法流程如图2所示。

图2 湍流积分长度数值预报方法流程Fig.2 Procedure diagram of numerical prediction on anisotropic turbulence integral length
1.1 k-ω模式
Wilcox(2007)[10]提出了k-ω模式的修正模式Shear-Stress Transport(SST)k-ω模式,在ω(ε和k的比率)控制方程中引入了计入阻尼影响的导数扩散项,通过引入湍流切变应力修正了涡粘性系数,并且修改了部分封闭方程的常系数。SST k-ω模式实际上混合了k-ω模式和k-ε模式,使得模式同时具有了k-ω模式计算近壁面区域粘性流动的可靠性和k-ε模式计算远场自由流动的精确性。湍动能k和耗散率ε的控制方程为:

1.2 LES及DKET 亚格子模式
在获得定常流场后,通过LES计算脉动的速度场,LES的基本思想是直接计算大尺度脉动,而对小尺度脉动做模式,因此首先要把小尺度脉动过滤掉,本文假定过滤过程和求导过程可以交换,对Navier-Stokes方程作过滤运算,可得到LES控制方程为[11]
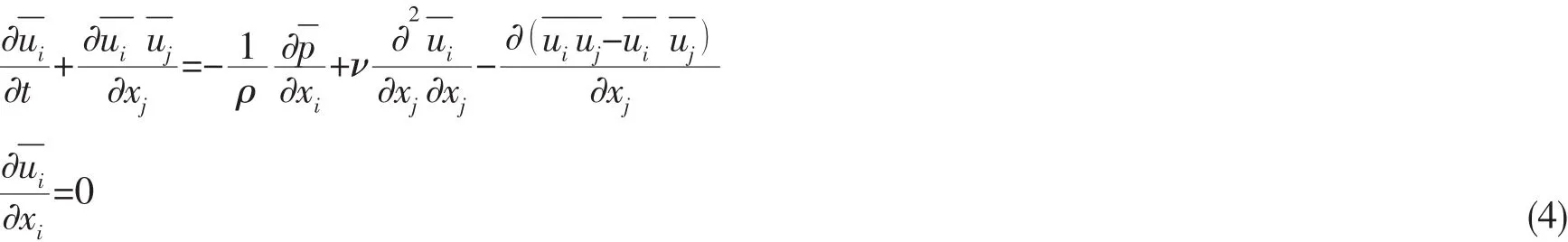
方程(4)右端有不封闭项

式中:τij为亚格子应力,代表过滤掉的小尺度脉动和可解尺度湍流间的动量输运,需要模化,本文采用DKET亚格子模式[12]进行封闭。
该模式通过亚格子湍动能来定义粘性系数

式中:Δ=V1/3是亚格子尺度是亚格子湍动能。
亚格子应力表达式为:

亚格子湍动能通过求解湍动能输运方程来封闭:

式中:νt为粘性系数,

1.3 湍流积分长度计算式
湍流积分长度是指流场中最大尺度涡结构的量度,即大涡的尺度,湍流积分长度主要有下面三种定义[9]:(1)基于流场中两点速度的相关函数;(2)基于湍流中的某些物理特征长度(例如流场中涡的半宽长度或者固壁面边界层中的动量厚度);(3)基于湍流波谱最佳拟合函数,通过调整湍流积分长度和湍流度来使得假设的曲线能够以最小误差吻合湍流波谱。上述三种积分长度的定义都是针对基于各向同性假设和Taylor冷冻假设的传统积分长度,对于普遍存在的各向异性湍流积分长度并不能很好地进行函数表达。因此,本文采用Blake提出的基于互功率谱卷积定义的各向异性湍流积分长度[9],具体定义和计算公式如下。
(10)式定义了湍流的系综平均:

对于平稳过程中系综平均等于随机过程的时间平均,则湍流的系综平均可以表示为

则流场中任一点的脉动速度为

定义“速度的j分量在ri方向上的湍流积分长度”,


定义式中delta函数为



式中:αc是r2方向上的湍流涡团拉伸参数,若要计算r2方向上的积分长度,只需将拉伸参数αc改成βc即可是各向同性湍流积分长度,可以由下式求得:


式中:r为两点的间距。
2 算例分析
2.1 二维水翼各向同性湍流积分长度
本节通过与国际上已被广泛应用于随边湍流和辐射噪声研究的二维水翼的PIV和TR-PIV(高速PIV)试验数据进行对比分析,验证了各向同性湍流积分长度的数值预报方法。二维水翼弦长为364 mm,厚度为20.32 mm,展长为450 mm。水翼头部为5:1的椭圆,中间为平板,下表面为平面,上表面尾缘部分为与下表面夹角为45°的圆弧,水翼模型的剖面示意图及坐标如图3(a),图3(b)是PIV测量流场区域示意图,图3(c)给出了湍流积分长度计算取点位置,试验在中国船舶科学研究中心空泡水筒中进行[6]。计算域网格如图4,网格总量27万。

图3 试验模型示意图Fig.3 Schematic diagram of experimental model

图4二维水翼计算域网格Fig.4 Mesh 2-D hydrofoil
图5比较了试验和数值计算的结果。

图5 不同位置剖面湍流积分长度预报结果与试验比较Fig.5 Comparison between numerical and experimental data of turbulence integral length at different locations
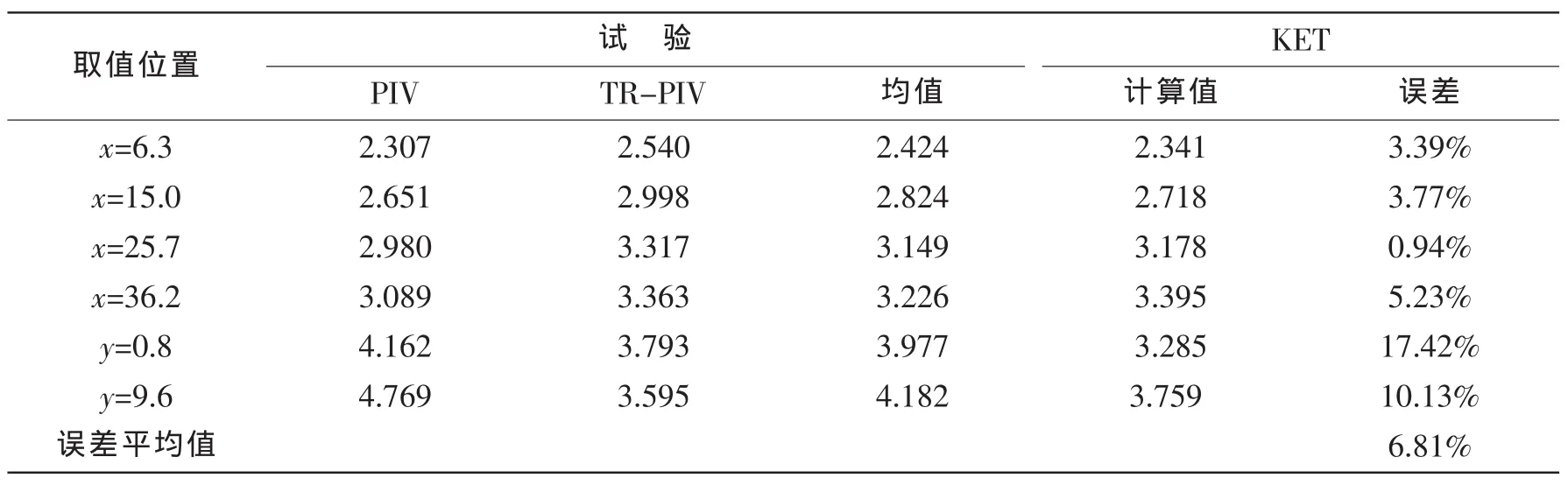
表1 各向同性湍流积分长度计算试验结果比较Tab.1 Comparison between numerical and experimental results of isotropy turbulence integral length
从图5中可以看出,DKET亚格子模式基本反应出湍流积分长度的结构特征:(1)对于近随边(x= 6.3,15 mm)区域的高湍流度部分(-20 mm≤y≤15 mm),CFD计算出了显著的双峰结构,并且在x=15 mm处双峰间距大于x=6.3 mm处,反应出漩涡的扩散;但是计算的两峰间隔较试验结果偏大,即CFD流场计算时漩涡涡核间距偏大。(2)对于稍远离随边(x=25.7,36.2 mm)区域,在(y≤0 mm)部分,计算结果与试验结果较吻合,波峰稍偏左,这是由于之前的涡核间距计算偏大;在(y>0 mm)部分,计算峰值比试验结果小1 mm左右。(3)对于y=0.8,-9.7 mm两个剖面,y=0.8计算偏差较大,而y=-9.7 mm计算较为精确。总体情况来看,在y≤0 mm区域计算的较为准确,而在y>0 mm区域偏差较大。表1给出了不同剖面上试验和计算结果的均值。
从图5及表1可以看出,数值计算的湍流积分长度能满足预报精度要求。
2.2 空气螺旋桨各向异性湍流积分长度
Blake(2002)在文献[9]中给出了各向异性湍流积分长度的试验及数值预报方法,计算公式在1.3中给出,试验相关参数见表2,图6给出了试验结果、Blake计算结果和本文计算结果。

表2 试验相关参数Tab.2 Test parameters
图中实线是本文计算结果,虚线是Blake[9]的计算结果,从图中可以看出,本文计算的无论是与Blake的计算结果还是试验结果都较为接近,验证了各向异性积分长度计算方法的计算精度。

图6 计算及试验结果Fig.6 Numerical prediction and experimental data of
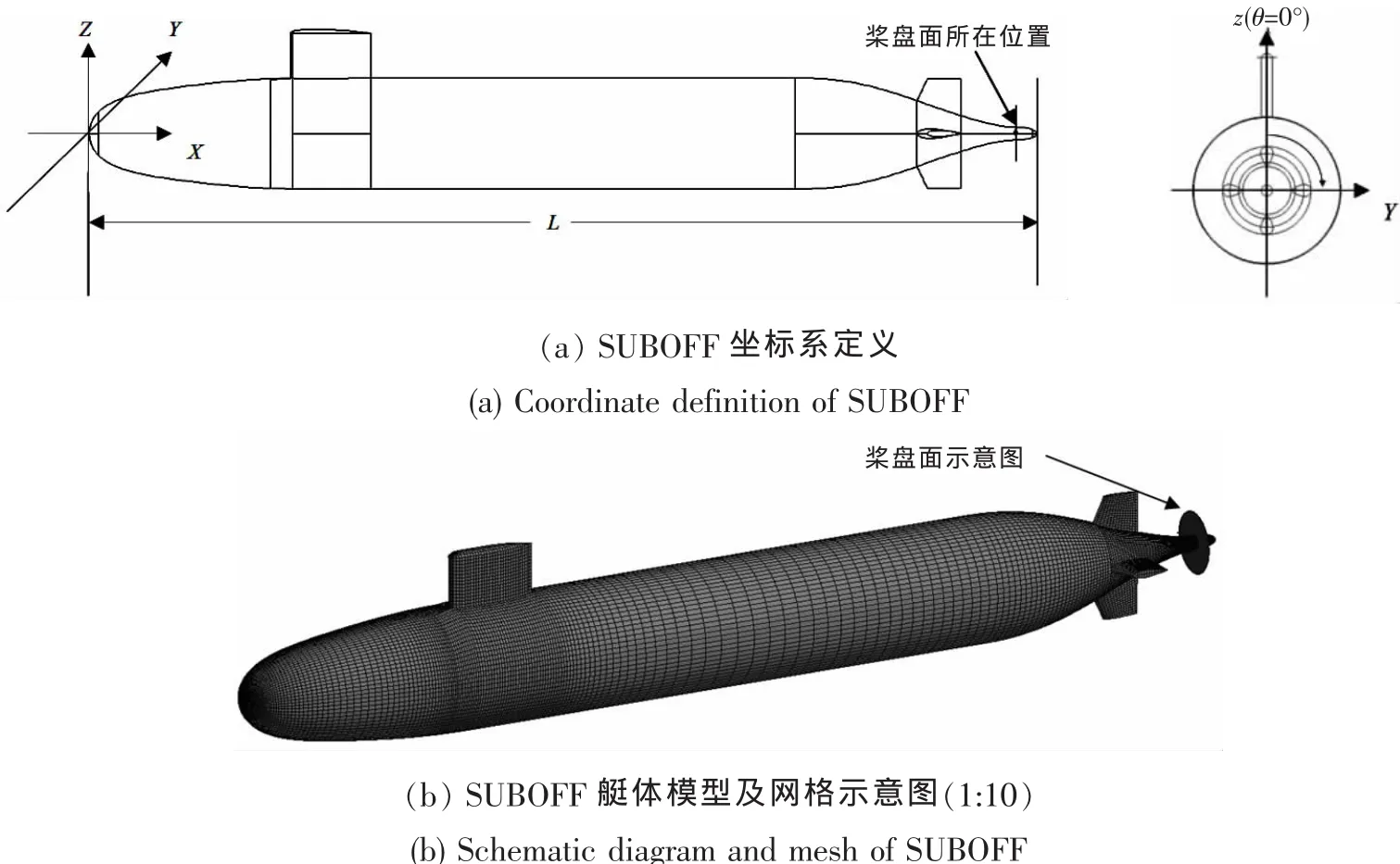
图7 SUBOFFFig.7 SUBOFF
2.3 SUBOFF艉部湍流积分长度预报
2.3.1 模型尺寸及网格划分
本节采用美国国防部先进研究项目局(DARPA)提出的SUBOFF AFF-8标准模型为研究对象,研究潜艇艉部桨盘面处湍流积分长度的数值预报,并且对相关特性进行了研究。
SUBOFF AFF-8带有指挥台围壳和十字型稳定翼,总长L=4.356 m,进流段长1.016 m,平行舯体长2.229 m,最大直径D=0.508 m,去流段长1.111 m(后体端部长 0.095 m),稳定翼后缘位于4.007 m处。指挥台围壳前缘位于0.924 m处,后缘位于1.923 m处,长0.368 m,高0.460 m,其截面为椭圆,长短轴比为2:1,顶部为有外凸的椭圆盖。桨盘面位于x/L=0.978处,直径d=D/2。具体外形参见文献[13]。坐标系定义及网格如图7,网格总量1 200万。
2.3.2 流场计算结果验证
图8对比了指挥台围壳0.1H、0.5H和0.9H高度处(指挥台围壳总高度为H)压力系数的试验和计算结果,图9对比了桨盘面上r/R=0.25处三向平均速度和湍动能的周向分布,在图10中对比了轴向速度周向平均值沿径向分布。

图8 指挥台围壳不同高度压力系数比较:(a)h=0.1H,(b)h=0.5H,(c)h=0.9HFig.8 Pressure coefficient comparison at different height of the fairwater

图9桨盘面上r/R=0.25处的计算及试验值比较Fig.9 Comparison between calculation and experiment at r/R=0.25
图8和图9的计算结果与试验及与Bull[13]的比较分析可以看出,本文的CFD计算结果无论是在艇前部指挥台围壳处,还是艇艉桨盘面处的流场计算,均有较高的精度,可以作为计算湍流积分长度的流场输入。
2.3.3 桨盘面处湍流积分长度
本节数值预报了SUBOFF桨盘面处各向异性湍流积分长度,图10给出基于速度相关函数的湍流积分长度不同半径处周向分布和周向平均值的径向分布。

图10 计算结果Fig.10 Calculation results of
从图10(a),(b),(c)可以看出,受到指挥台围壳和稳定翼马蹄涡的影响,湍流积分长度在20°和90°附近出现峰值;受涡团扩散影响,外半径湍流积分长度要大于内半径。图10(d)可以看出三向速度的湍流积分长度的周向平均随径向变化趋势大致一致;在内半径处三个湍流积分长度数值上大小较为一致,在外半径数值上差别较小,而与差别较大,这是由于内半径湍流的各向异性较弱,而外半径随着涡团的扩散,湍流的各向异性逐渐增强。


图11 不同半径处的频率分布Fig.11 Frequency distribution ofat different radius


图12 不同频率在不同周向位置的径向分布Fig.12 Radial distribution ofat topic frequency at different circumferential locations
3 结 语
本文对潜艇艉部湍流积分长度进行了数值预报及研究,首先通过与二维标准水翼和风洞三维螺旋桨试验数据比较,分别验证了二维水中各向同性和三维风洞各向异性湍流积分长度的数值预报方法;然后对SUBOFF艉部各向异性湍流积分长度进行了预报研究,得出以下结论:
(1)指挥台围壳和稳定翼马蹄涡对艉部涡团位置有明显影响,周向波峰出现在20°和90°左右;受涡团扩散影响,径向分布外半径积分长度要大于内半径;
(2)指挥台围壳和稳定翼马蹄涡脱落频率(约15 Hz)对的频率峰值有明显影响,峰值集中在30 Hz以下;径向分布整体呈现外半径大于内半径趋势;潜艇上部涡团扩散较下部明显,导致内半径波峰随着角度增大而内移。
下一步工作将集中在对各向异性湍流积分长度的机理研究和通过各向异性湍流积分长度构造新的湍流波数谱并评估对低频宽带噪声的影响这两个方面。
[1]Blake W K.Mechanics of flow-induced sound and vibration[M].New York:Academic Press,1986:735-756.
[2]Kirschner I N,Corriceau P J,Muench J D.Validation of propeller turbulence ingestion acoustic radiation model using wind tunnel measurements[C].Louisiana:Flow Noise Modeling,Measurement and Control,ASME,1993:175-186.
[3]朱锡清,唐登海,孙红星.船舶螺旋桨低频噪声研究[J].水动力学研究与进展,2000,15(1):74-81.Zhu Xiqing,Tang Denghai,Sun Hongxing.Study of low-frequency noise induced by marine propeller[J].Chinese Journal of Hydrodynamics,2000,15(1):74-81.
[4]朱锡清,李 亚,孙红星.船舶螺旋桨叶片与艉部湍流场相互作用噪声的预报研究[J].声学技术,2006,25(4):361-364. Zhu Xiqing,Li Ya,Sun Hongxing.Prediction of noise induced by interaction between turbulence flow and propeller blades [J].Technical Acoustics,2006,25(4):361-364.
[5]熊紫英,孙红星,朱锡清.入射湍流与螺旋桨相互作用的低频宽带噪声预报研究[J].中国造船,2014,55(3):3-11. Xiong Ziying,Sun Hongxing,Zhu Xiqing.Prediction of low-frequency broadband noise induced by the interaction between injected turbulence and propeller[J].Shipbuilding of China,2014,55(3):3-11.
[6]张国平.空泡水筒中湍流参数PIV试验测量和分析方法研究报告[R].无锡:中国船舶科学研究中心,2010. Zhang Guoping.Comparison on turbulence measurement and analysis methods in cavitation tunnel by Particle Image Velocimeter[R].Wuxi:China Ship Scientific Research Center,2010.
[7]谢 华,刘建华,田于逵.湍流积分长度的HWA与LDA联合测试分析方法研究[C]//第十三届船舶水下噪声学术讨论会论文集.中国鹰潭,2011:345-350. Xie Hua,Liu Jianhua,Tian Yekui.Research and analysis on HWA and LDA joint test of turbulence integral length[C]// Proceedings of 13st Symposium on Underwater Noise.Yingtan,China,2011:345-350.
[8]刘建华,谢 华,田于逵.湍流积分长度新型联合测试方法研究[C]//第二十三届全国水动力学研讨会暨第十届全国水动力学学术会议论文集.中国西安,2011:283-289. Liu Jianhua,Xie Hua,Tian Yukui.Validation of a new method for turbulence integral length measurement based on a HWA and LDA combined system[C]//Proceedings of 23st Symposium on National Hydrodynamics.Xi’an,China,2011: 283-289.
[9]Lynch D A,Mueller T J,Blake W K.A correlation length scale for the prediction of aeroacoustic response[C]//AIAA. Colorado,2002.
[10]Wilcox D C.Formulation of the k-ω turbulence model revisited[C].Reno:45th AIAA Aerospace Sciences Meeting and Exhibit,2007.
[11]张兆顺,崔桂香,许春晓.湍流理论与模拟[M].北京:清华大学出版社,2005.
[12]Won-Wook,Suresh Menon.Application of the localized dynamic subgrid-scale model to turbulent wall-bounded flows [R].Reno:Technical Report AIAA-97-0210,1997.
[13]Bull P.The validation of CFD prediction of nominal wake for the SUBOFF fully appended geometry[C]//Proceedings of 21st Symposium on Naval Hydrodynamics.Norway,1996.
Numerical prediction and research on anisotropic turbulence integral length
JIANG Jing-wei1,MA Cheng1,QIAN Zheng-fang1,2,CHEN Ke1,CAI Hao-peng1,ZHANG He3
(1 Naval Academy of Armament,Beijing 100161,China;2 Naval Univ.of Engineering,Wuhan 430033,China; 3 China Ship Research and Development Academy,Beijing 100101,China)
This paper proposes a numerical method to predict the anisotropic turbulence integral length in view of this situation that the classic(isotropic)turbulence integral length is mainly acquired from experiments.Where RANS is utilized to predict the initial steady flow field;LES is used to calculate fluctuating velocity;the classic turbulence integral length is calculated based on cross-correlation function and the anisotropic turbulence integral length is finally predicted.The numerical method to predict isotropic turbulence integral length is validated the experimental data from 2-D hydrofoil,and the average error is 6.81%; and anisotropic turbulence integral length prediction method is validated by wind tunnel test.Then the anisotropic turbulence integral length of SUBOFF is studied and understood:the integral lengths at outside radius are lager then those at inside radius in all directions;the vortexes in the upper part diffuse more intensely than that in the under part,leading to the peak bars moving inside along with the angle increasing; the peak bars oare all near 20°and 90°according to the exists of horse-shoe vortexes of conning tower and stabilizers;The peak frequency ofare both lower than 30 Hz as theshedding frequency of the horse-shoe vortexes is about 15 Hz.The current work lays the foundation of constructing new turbulence spectrum to improve the accuracy of prediction of low-frequency broadband noise.
anisotropic turbulence integral length;numerical prediction;CFD; Large Eddy Simulation,LES
U661.1
A
10.3969/j.issn.1007-7294.2015.10.001
1007-7294(2015)10-1161-12
2015-06-08
国家自然科学基金资助项目(No.51079158)
蒋靖伟(1991-),男,硕士研究生,E-mail:15365286622@163.com;
马 骋(1963-),男,研究员,博士生导师,E-mail:Macheng50089@yahoo.com.cn。

