LBM方法数值模拟飞溅流动的影响因素研究

韩文骥，颜开，褚学森，张珂

（中国船舶科学研究中心水动力学重点实验室，江苏无锡214082）

LBM方法数值模拟飞溅流动的影响因素研究

韩文骥，颜开，褚学森，张珂

（中国船舶科学研究中心水动力学重点实验室，江苏无锡214082）

文章采用格子Boltzmann单相自由面模型模拟飞溅流动问题，以楔形体入水问题为模拟对象，研究了网格精细度、计算域、水动力相似参数对飞溅效果的影响。研究表明，亿量级网格下入水飞溅射流及飞溅端部的细小液滴结构十分清晰，模拟结果明显优于百万量级、千万量级网格；计算域超过模型尺度3倍后飞溅效果不受影响；以自由液面面积S的增长率η为比较参数，当Re数、Fr数较小时对飞溅效果有明显影响，大于一定数值后，飞溅效果基本一致。

网格精细度；LBM；单相自由面模型；飞溅流动

0 引言

飞溅流动是在自然界和工程应用中经常遇到的多相流动问题，如海浪击岸的浪花飞溅，船舶甲板上浪飞溅，鱼雷等钝头体入水飞溅等多种问题。强烈的飞溅，如恶劣工况下飞溅的海浪可以破坏船舶的上层建筑，物体入水的载荷与弹道姿态也与飞溅流动相互耦合。因此研究飞溅流动形成机理、流场结构，是研究相关载荷评估、弹道预报等工程问题的基础。

大量的间断、复杂的几何拓扑是飞溅流动的最大特征。这类问题具有非线性、非定常的特征，很难用简单的理论模型描述飞溅过程。LBM方法更能够有效处理大量细小、分散界面的飞溅流动问题。首先，LBM方法基于统计物理学，以迁移和碰撞的形式描述粒子微团的运动特征，采用一个简单的离散速度集合来反映整个速度场的平均信息，简单完整地描述了流体运动；而且LBM方法理论基础是建立在分子运动论的观点上，受宏观流体介质特性的束缚较小，适合处理多相流动；最后，LBM方法中不管是迁移还是碰撞过程都是在流体的局部发生，易于并行处理，非常适合做大规模的计算。

本文采用单相自由面LBM模型[1]模拟飞溅流动，结合大涡模拟和运动边界处理方法，分析网格精细度、计算域大小、Re数、Fr数等因素对模拟飞溅效果的影响。在这些研究中皆采用MPI编程标准对程序予以加速。

1 数值模型

1.1 格子Boltzmann单相自由面模型

飞溅流动是气液两相流问题。本文采用Thürey提出的格子Boltzmann单相自由面模型[1]，该模型适合处理界面大幅变形的气液两相流动问题。此模型包含气相、液相、界面三类格点，但只描述液相格点的演化方程：

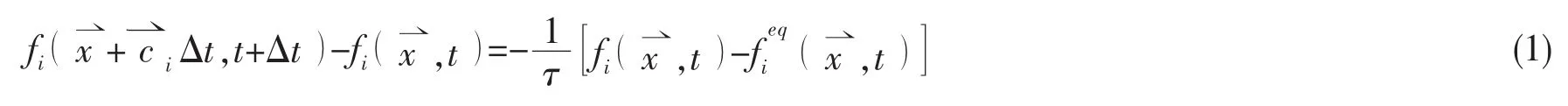
从气相格点迁移至液相格点（即i方向）的未知分布函数由此得到，下标表示i的反方向，ρA与大气压有关。为模拟自由面运动，该模型在每时间步内计算界面格点的质量变化：

并将满足某类状态的格点的多余质量分配到周围格点中去，以此模拟界面的真实运动。多余质量的分配与该格点的界面法向量有关[1]。

1.2 大涡模拟—Smagorinsky模型

应用单相自由面LBM模型模拟工程实际中的飞溅流动，处理高Re数流动时需加入湍流模型满足数值稳定性。本文采用大涡模拟方法，大涡模拟最早由Smagorinsky提出，其基本思想为：直接数值求解大尺度紊流运动，并利用次网格尺度模型模拟小尺度紊流运动对大涡的影响。Smagorinsky模型应用Boussinesq假设，在运动粘性系数中引入涡粘性系数修正；然后结合普朗特的混合长度理论，得到涡粘性系数与速度梯度、小涡尺度之间的关系[3]。LBM方法的Smagorinsky模型中心思想为通过涡粘度修正松弛参数，以实现湍流模拟。修正后的松弛参数为：

观上式可知，对松弛参数的修正其实正是对运动粘性系数的修正。修正项中Cs为模型算子，与小涡尺度有关。S为局部应力张量：

1.3 运动边界处理

飞溅流动往往因物体与水面的撞击而产生，因此物面的边界处理尤为重要。本文采用Bouzidi等人发展的BFL格式处理物面边界[4]，如图1，采用插值方法得到未知的由于内插格式数值稳定性好，q＜1/2时，选用t时刻格点的分布函数插值：

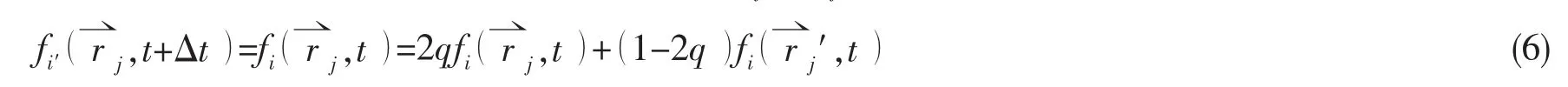
图1 BFL格式插值过程示意图Fig.1 The interpolation sketch map of BFL format

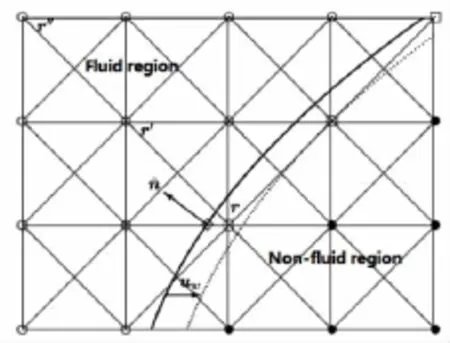
图2 速度为w的运动边界示例Fig.2 Illustration of a moving boundary with velocityw

上面讨论的是静止壁面，对运动壁面，需在（6）式和（7）式中添加壁面运动对流体分布函数的影响，其形式为：

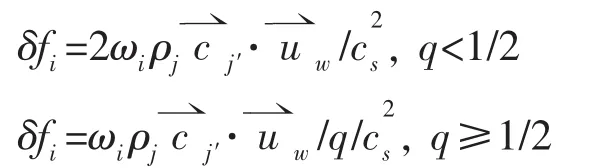
要将上述边界条件扩展到运动边界，还需要注意下面的问题，如图2，图中实、虚曲线分别为t和t+△t时刻壁面边界位置。在t+△t时刻，格点⇀r从非流体区域移到流体区域成为流体格点时，其分布函数未知。本文采用文献[5]中的方法，采用二阶插值构造该格点上的分布函数：

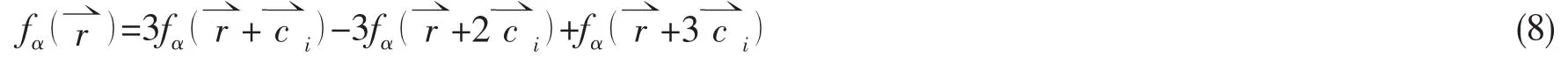
2 结果及分析

本文数值模拟的算例是楔形体入水，楔形体入水的真实飞溅现象可参考莫立新等人[6]实验研究中的入水飞溅形态，如图3。本文数值模拟采用的楔形体构型如图4所示，β=30°且Lx:Ly=2:1。模拟终止时间为楔形体入水两倍体高的时刻。

首先对Re=2×106、Fr=2.78时三种网格精细度下楔形体入水的飞溅流动作了三维数值模拟。对应的计算域分别为200×100×100（百万量级）、400×200×200（千万量级）、800×400×400（亿量级），特征长度Lx分别为40、80、160格子长度，楔形体在计算域中的相对位置不变。

模拟结果如图5。首先对比整体飞溅效果，图5（a）中自由面有一定幅度的变形，但未见真实飞溅流动中的精细结构，自由面轮廓整体较光滑；图5（b）中飞溅端部自由面有剧烈变形，且局部自由面有破碎的趋势，细小液滴有了飞溅雏形；图5（c）中无论自由面的变形幅度，还是飞溅端部分散出的细小液滴结构，都表明亿量级网格精细度下的模拟结果最接近真实的飞溅流动现象。其次，以飞溅射流这一流动特征为对象进一步分析网格精细度对模拟结果的重要影响。射流偏角(射流与入水速度的夹角)的差异最为明显，对比图5（a）、（b）、（c）发现射流偏角逐渐增大，且增幅明显；接着观察射流薄层，图5（a）中薄层很厚且飞溅幅度小，图5（b）中薄层扁平且飞溅幅度大幅提升，图5（c）中薄层飞溅幅度进一步提升，且端部破碎并生成了分散的细小液滴结构。综上可知，网格精细度显著影响飞溅流动精细结构的模拟精度，且亿量级网格精细度或者说Lx=160格子长度下，模拟结果明显更接近真实飞溅流动。图5是楔形体入水的正视图，为直观感受亿量级网格下入水飞溅的三维效果，本文以图3中实验视角展示了其入水过程的十个阶段，如图6。在整个入水过程中，能够观察到显著的飞溅射流，这与图3入水前期的飞溅形态相似；在入水前五个阶段，飞溅射流逐渐生成，并在射流前端衍生出细小水花结构；在后五个阶段，随着入水阶段的不断推进，首批衍生出来的细小水花结构开始脱落，飞溅射流冲溅到距离水面更高的位置，并有新的细小水花结构开始随着整体射流回落，这与图3入水后期的飞溅形态相似。因此，亿量级网格下模拟得到的入水过程较真实地再现了入水飞溅的自由面变化形态。

图3 楔形体入水的飞溅形态Fig.3 Splashing of wedge water-entry

图4 三维楔形体构型Fig.4 Three-dimensional configuration of the wedge

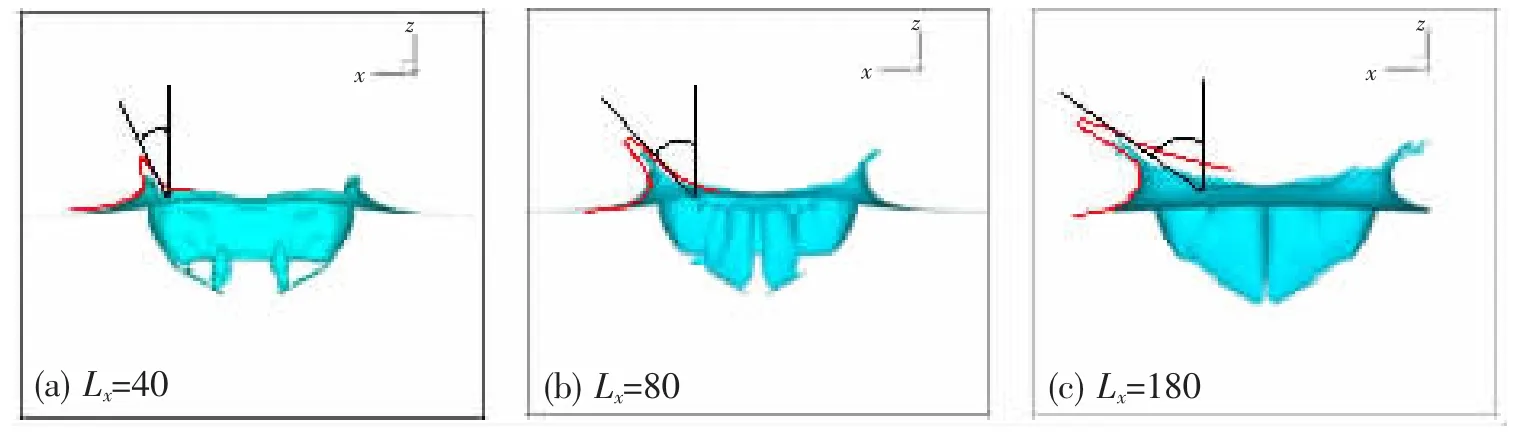
图5 不同网格精细度下的楔形体入水模拟结果；红线为飞溅射流轮廓线，黑线为射流偏角标示线Fig.5 Simulation results of wedge water-entry with different grid refinement; red line:splashjetcontour,black line:jet angle marking line

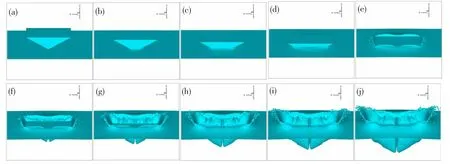
图6 楔形体入水的飞溅过程Fig.6 Splashing of wedge water-entry

本文底面边界采用插值叠加边界[7]，其他计算域边界采用远场边界。为精确且高效地数值模拟飞溅流动，本文探讨了计算域大小对模拟结果的影响。选用亿量级网格即Lx=160，分别对X向维度NX= 2Lx、3Lx、5Lx、7Lx（Y、Z同比例变化）的模拟结果作了比较。NX=2Lx时，计算后期数值发散，其余模拟结果如图7。对比发现NX=3Lx、5Lx、7Lx三类计算域下，入水模拟结果十分接近，无论是飞溅幅度，还是飞溅射流尖端的细小液滴结构，皆大体相当。因此在满足数值方法稳定可解的条件下，计算域大小不显著影响模拟精度，考虑到工程应用的经济性，可采用3倍模型尺度的计算域进行数值计算。

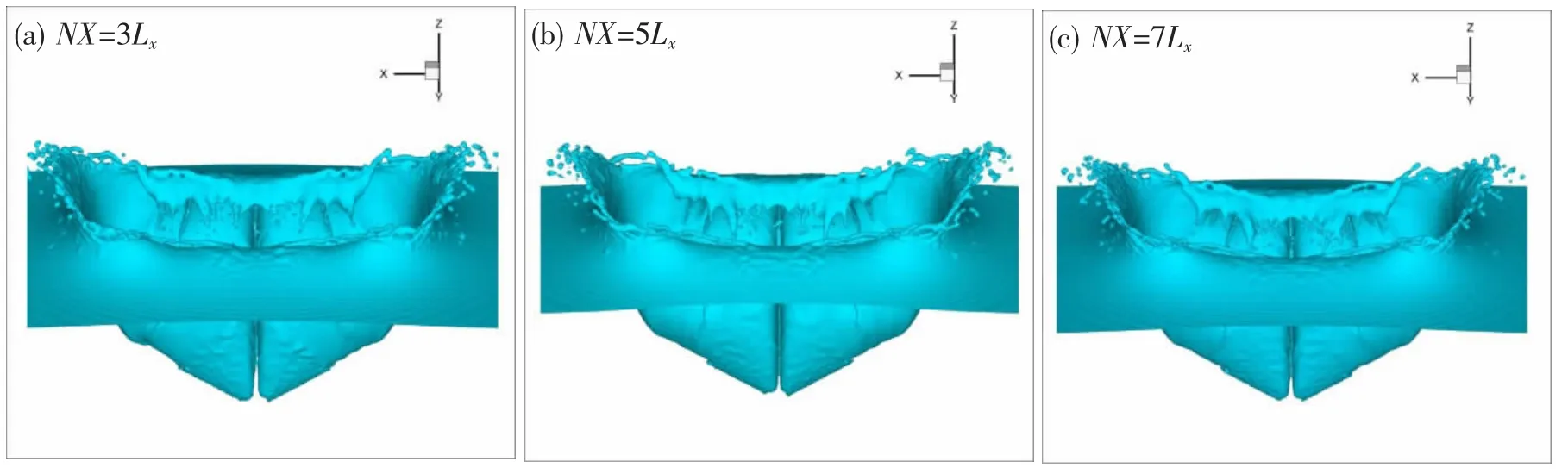
图7 同种网格精细度下不同计算域的飞溅效果Fig.7 Splash effect with different computational domain under the same grid refinement

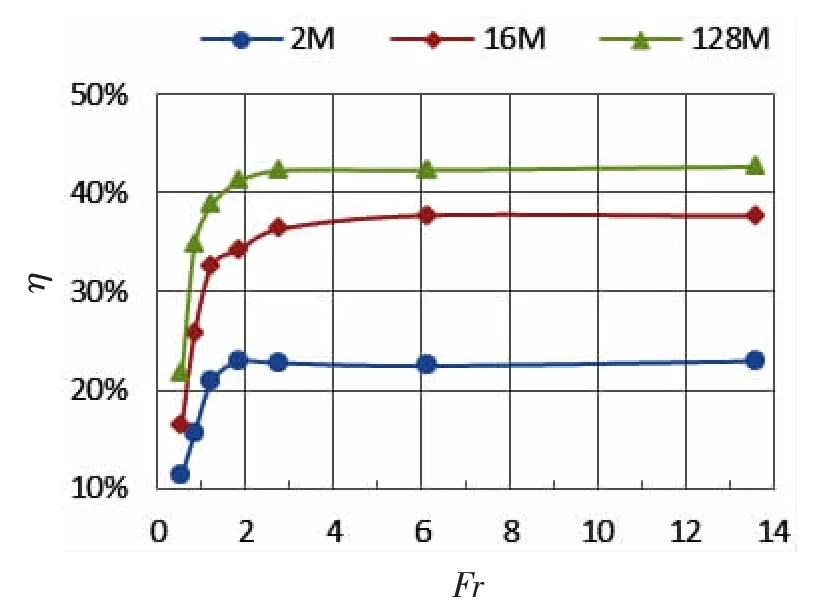
图8 （a）三种网格下飞溅效果与Fr数的关系曲线Fig.8(a)Splash effect curve with different Froude numbers under three grids

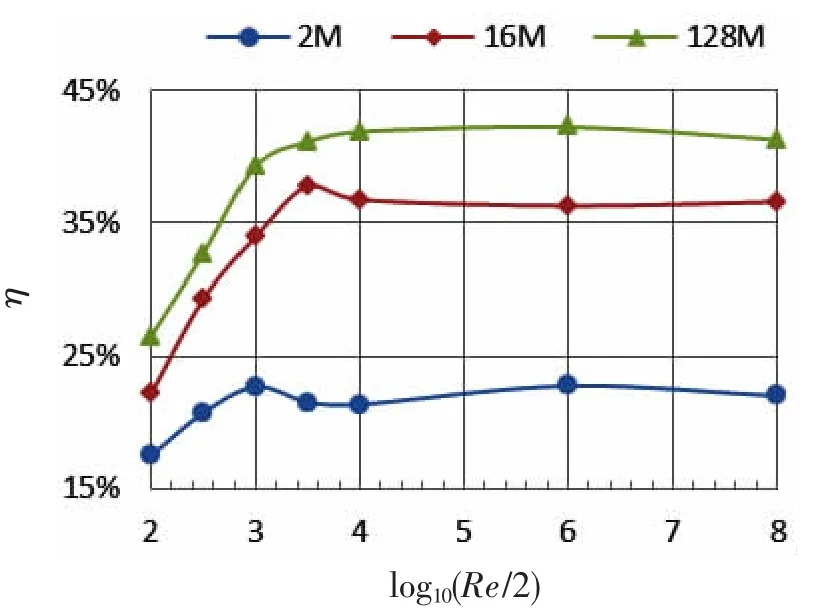
图8 （b）三种网格下飞溅效果与Re数的关系曲线Fig.8(b)Splash effect curve with different Reynolds numbers under three grids

三种网格下入水飞溅效果与Fr数、入水飞溅效果与Re数的关系曲线分别如图8（a）、（b）所示。由图8（a）可知，Fr数在0.57～1.88区间内变化时，三种网格下的飞溅效果皆显著提升；Fr数在1.88～6.12区间内，三种网格下的飞溅效果增长幅度放缓并趋于平滑，虽然百万网格下的飞溅效果在Fr＞1.88后便稍微下降，但其整体趋势与其他两种网格是一致的；在Fr＞6.12之后，飞溅效果基本相当。由图8（b）可知飞溅效果随Re数的变化规律与Fr数类似。飞溅效果增长最显著的Re数区间为200～2×103；Re数在2×103～2×106区间内，三种网格下的飞溅效果变化趋势虽有差异，但它们的变化幅度都较小，参考图5中显示的网格精细度对LBM模型刻画飞溅精细结构的影响，以及图6中亿量级网格描述自由面飞溅过程的复杂、精细程度，此处三种网格下的飞溅效果变化不一致，应是百万网格和千万网格对自由面分离、合并过程的刻画能力不足，导致采用自由面面积增长率η为量化依据得到的结果有些失真，因此亿量级网格下的飞溅效果在此Re数区间内的变化趋势是真正符合真实流动现象的；最后，Re在2×106以上时，飞溅效果几近相同。

由数值结果及以上分析表明，飞溅效果随Fr数、Re数的变化规律与数值模拟飞溅流动所采用网格的精细程度并无明显依赖关系；因亿量级网格下的模拟结果最能刻画飞溅特征，本文展示此网格下模拟得到的上述不同Fr数、Re数的自由面飞溅形态，以直观感受飞溅效果随Fr数、Re数的变化规律，如图9。由图9（a）可知，Fr=0.57、0.86、1.25、1.88变化时，自由面的闭合形态有显著变化，且飞溅射流端部的细小液滴也愈加趋于精细；在Fr＞2.78之后自由面的飞溅形态并无显著差异。由图9（b）可知，Re=200、2×102.5、2×103、2×103.5变化时，飞溅的细小液滴结构逐次增多；Re＞2×104之后自由面的整体形态及细小液滴结构均无明显变化。这些都与上述量化分析得到的结论相吻合。

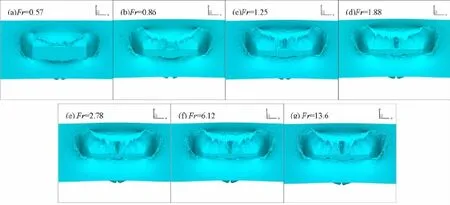
图9 （a）不同Fr数下自由面的飞溅形态Fig.9(a)Splash of the free surface under different Froude numbers

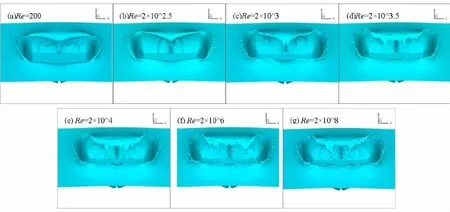
图9 （b）不同Re数下自由面的飞溅形态Fig.9(b)Splash of the free surface under different Reynolds numbers

3 结语

本文采用格子Boltzmann单相自由面模型，并结合运动边界及大涡模拟方法，对飞溅流动的影响因素作了综合分析。研究表明，网格精细度对飞溅流动宏观结构的刻画具有很大影响，在亿量级网格下模拟楔形体入水，可以模拟更真实的飞溅流动。其次，在计算稳定的条件下，计算域大小对模拟结果无明显影响，对楔形体入水问题而言，NX=3Lx即可得到理想结果。此外，研究表明Re数在2×104以下、Fr数在2.78以下时，本文采用的LBM模型能够有效刻画Re数、Fr数对飞溅流动精细结构的影响。

[1]Thüery N.Physically based animation of free surface flows with the Lattice Boltzmann Method[D].Freistaat Bayern:University of Erlangen-Nuremberg,2007.

[2]Buick J M.Lattice Boltzmann methods in interfacial wave modeling[D].The Towns of Edinburgh：University of Edinburgh, 1997.

[3]王玲玲.大涡模拟理论及其应用综述[J].河海大学学报（自然科学版）,2004,32(3):261-265. Wang L L.Review of large eddy simulation theory and its application[J].Journal of Hohai University(Natural Sciences), 2004,32(3):261-265.

[4]Bouzidi M,Firdaouss M,Lallemand P.Momentum transfer of a Boltzmann-lattice fluid with boundaries[J].Phys.Fluids, 2001,13:3452-3460.

[5]Lallemand P,Luo L S.Lattice Boltzmann method for moving boundaries[J].J Comput.Phys.,2003,184:406-421.

[6]莫立新,王辉,等.变刚度楔形体板架落体砰击试验研究[J].船舶力学,2011,15(4):394-401. Mo L X,Wang H,et al.Study on dropping test of wedge grillages with various types of stiffness[J].Journal of Ship Mechanics,2011,15(4):394-401.

[7]张珂,颜开,褚学森,等.基于LBM方法的圆盘等速入水空泡的数值模拟[J].船舶力学,2010,14(10):1129-1133. Zhang K,Yan K,Chu X S,et al.Numerical simulation of constant speed water-entry cavity based on LBM[J].Journal of Ship Mechanics,2010,14(10):1129-1133.

Influence factors to numerical simulation of splash flow based on LBM

HAN Wen-ji,YAN Kai,CHU Xue-sen,ZHANG Ke
(China Ship Scientific Research Center,Wuxi 214082,China)

The single-phase free surface Lattice Boltzmann Model(LBM)is used to simulate the splash flow. Wedge water-entry problem is simulated to study the splash characteristics influenced by grid refinement, computational domain and hydrodynamic similarity parameters.The results show that the flow structure of the splash jet is much finer with a grid of hundreds million size compared to the coarse ones.With the computational domain of more than three times of the size of wedge,it could get almost the same splash characteristics.Reynolds number and Froude number will significantly affect the splash structure when they are in small values;while they are large enough,the splash images will keep similar.

grid refinement;LBM;single-phase free surface model;splash flow

O35

A

10.3969/j.issn.1007-7294.2015.04.002

1007-7294（2015）04-0356-07

2015-02-04

预研基金（9140A14010713CB32193）

韩文骥（1990-），男，硕士研究生，E-mail:hanwenji1990@aliyun.com；

颜开（1963-），男，研究员；褚学森（1980-），男，高级工程师。