多功能机床关键导轨副动态特性分析*＊

孙椰望 王 欣 刘 坤 李峰伦

(①北京理工大学机械与车辆学院，北京100081;②山东鲁南机床有限公司，山东 滕州277500)

快速保障性移动加工平台要求配备环境适用性多功能机床。然而，移动式加工环境存在较多的外部振动因素，从而影响到多功能机床的动态稳定性。而机床关键运动副部件的动态性能对于机床运行过程起到关键作用［1-2］。为了研究快速保障性复合机床在环境振动激励影响下的动态性能，必须深入研究机床关键导轨滑块运动副的动态特性。目前，机床动态特性的研究方法主要基于数值分析法和试验分析法，其中数值分析法动态模型的建立关系到计算结果的可靠性，并且数值计算终究需要试验法的验证［3-5］。所以，为了研究的时效性和可靠性，本文采用试验模态分析法对多功能机床关键滑块导轨部件进行动态分析。

1 机床导轨试验模态原理分析

如图1 所示，快速保障性多功能机床具有铣削和车削功能，铣削立柱依靠立柱滑块导轨副实现进给运动。因为铣削立柱具备独立运行特点，并且结构较高，所以在机床遭受环境振动载荷作用时处于机床整体系统的敏感响应区。特别是立柱导轨滑块运动副部件的动态性能成为铣削立柱动态特性的关键因素。

根据机床的运动特点对导轨滑块运动副进行受力分析如图2 所示，并得到导轨滑块运动副的X向和Y向动态方程为:

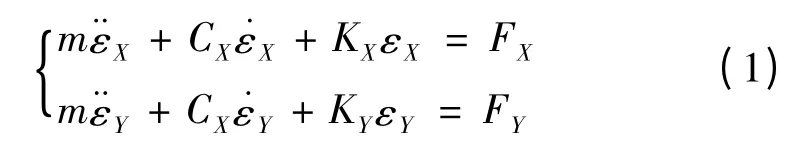
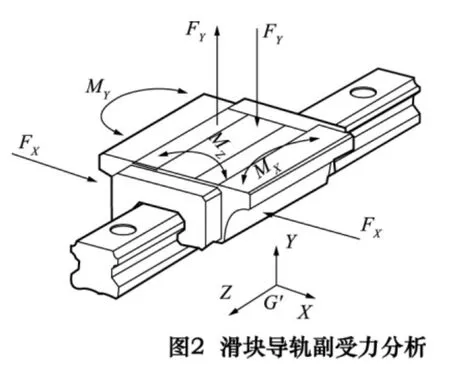
对其拉氏变换得到系统的传递函数方程为:

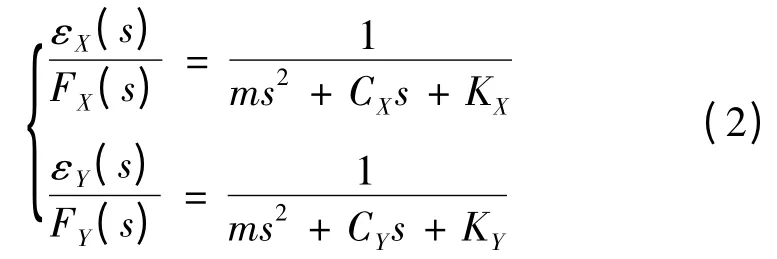
式中:εX、εY分别为导轨滑块运动副的X向和Y向位移，m;CX、CY分别为导轨滑块运动副的X向和Y向阻尼，N·s/m;KX、KY分别为导轨滑块运动副的X向和Y向刚度，N/m;m为单个滑块质量，kg。

为了研究立柱滑块导轨副的动态性能，需要求出导轨滑块副的传递函数以及刚度阻尼参数，并且获得其固有振动参数［6-7］。所以，本文分别对导轨滑块进行试验模态分析，其试验模态分析方案如图3 所示。

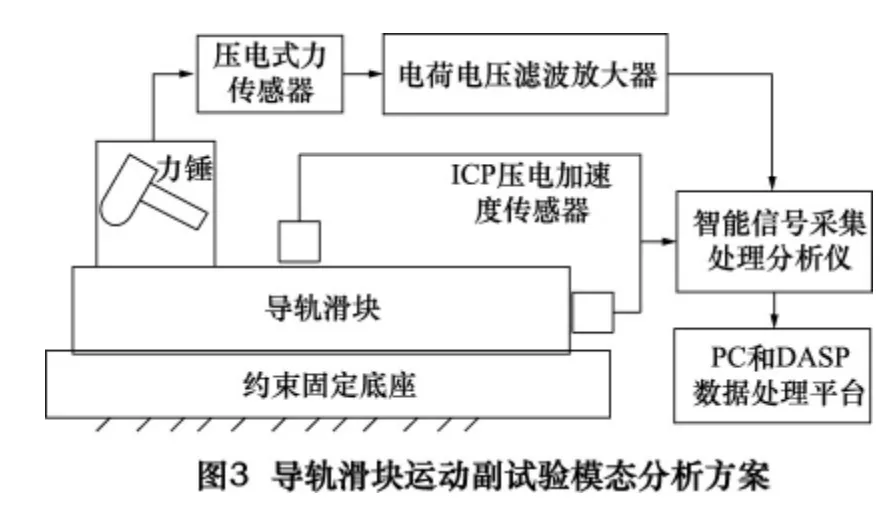
2 导轨滑块运动副的试验模态测试平台以及测点方案

多功能机床立柱滑块导轨副选用HG45CA 型导轨，其试验模态测试如图4 所示。为了确保试验的准确性，试验过程应该确保试验得到能够反映振动系统所有敏感响应区的数据及其振型，其模态试验必须能够得到滑块导轨副的X向和Y向的模态参数，为导轨滑块的动态分析提供弹性阻尼和刚度。所以，根据模态试验的目的和模态试验的特点，选择滑块导轨副的X和Y向进行输出响应测量原点。

为了能够尽量得到合适的振型(包含弯曲和扭转振型)滑块单方向至少布置3 个测点，于是根据导轨滑块的结构尺寸在测试对象的两个方向上各均布15个测点，如图5 所示。

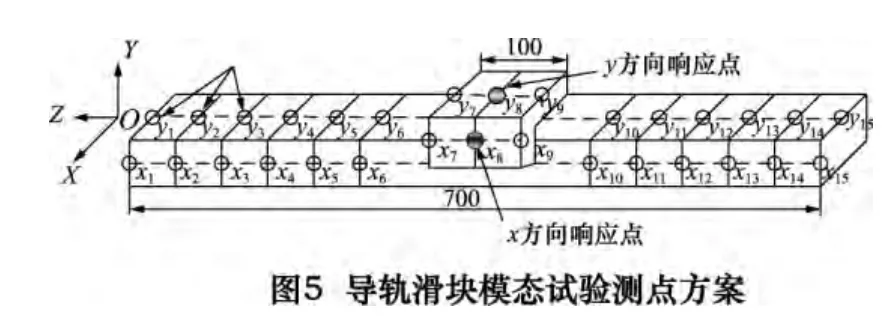
根据试验模态传递函数式(2)计算得到采样数据的传递函数矩阵见式(3)。根据图5 可知试验会得到的传递函数矩阵(3)的中间两行。根据传递函数矩阵的对称性特点可知试验结果能够满足导轨滑块完整的振动模态参数。

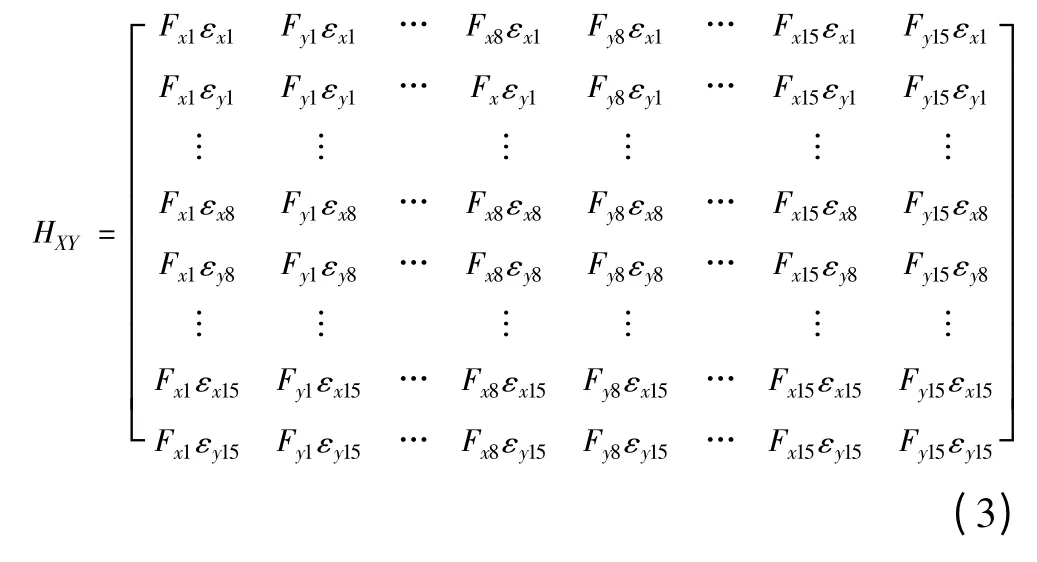
3 导轨滑块运动副试验模态分析

3.1 试验模态输出信号合理性分析

确定测量方案后，根据图4 和5 所示进行试验分析，为了获得高质量的测量和充分激起所有模态，如果选择的锤头太软，就不能充分激起所有这些模态［8-9］。相关研究［3，5］表明导轨滑块前5 阶固有频率在100 ～2 500 Hz之间，频率区域较大，所以本试验采用钢头。

该锤击法试验时，因为测量开始受到力脉冲陡度和外部信号的影响，力锤所在的通道是触发通道进行了预触发滞后设置。如果不使用特定的预触发滞后，响应信号会在初始阶段失真，从而增加数据分析误差。

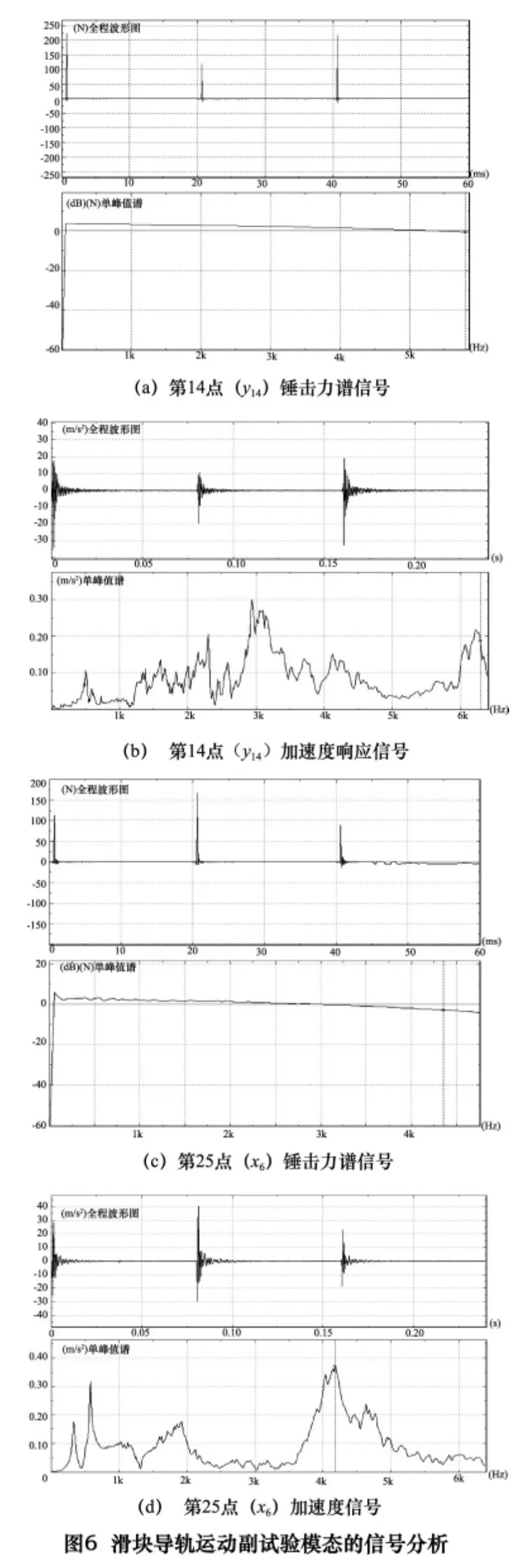
同时，为了激励的合理性和准确性，需要在同一位置锤击3 次，并实时观察力谱避免出现连击现象;并注意时域响应信号在感兴趣区的衰减情况，从而确保锤击的合理性。为了保证信号的一致性，每个测点进行多次锤击时，尽量保证是在同一点、同一个方向进行多次准确锤击，输入输出信号如图6 所示。

锤击模态试验数据的可靠性除了硬件的基本要求外，还需要判定采集信号的合理性。信号数据的合理性首要判据就是检查力锤激发信号的正确性和加速度传感器响应信号的合理性。根据图6 可知，该次试验具备以下特点:(1)力锤激发的力具备完整的力谱。(2)没有连击信号。(3)激发力激起了所有关心的频率。(4)在关心的激发频率范围内，力谱要具备平滑过度特点，并且整个范围内力谱衰减不能超过3dB。(5)加速度时域响应信号具备完整的衰减脉冲。根据试验模态信号合理性判定原则［10-11］可知该次试验测试信号输入与响应是准确的。

同时，图6 的加速度频谱信号所体现的是该点区域的振动特点，其中上升峰表明该点区域参与了整个振动系统的诸多振动，但是不能从单点的振动响应信号确定整个振动系统的模态特点。在锤击模态试验触发与接收信号合理性基础上，需要进一步分析输入与输出信号的耦合合理性。判别输入输出信号关联合理性的主要方法就是针对单点的振动响应所有采集的单点数据进行传递函数分析(transfer function analysis，TFA)。

3.2 试验模态传递函数分析

在锤击模态试验触发与接收信号合理性基础上，需要进一步分析输入与输出信号的相关性特点，这个相关性判据主要通过该点传递函数的相干程度来判定。一般情况下，在关心的研究频率范围内，测量点采集到的信号TFA 相干系数大于0.75 为合理，数值越接近于1，说明输出信号与输入信号的关联程度越大，并且说明该点的输出信号受到输入信号而激发的程度越高，试验越可靠［11］。

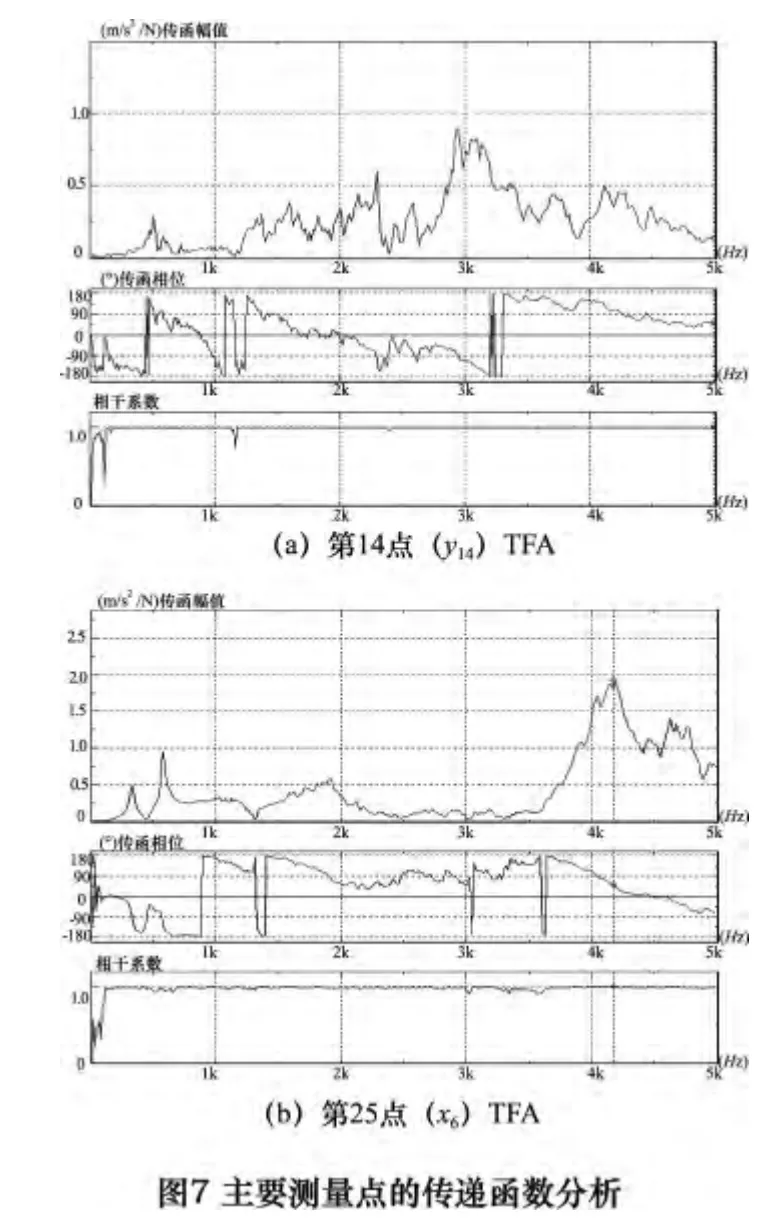
图7 所示为x6和y14点的TFA，根据图示可知单点测试的传递函数相干系数在研究的频率范围内都达到了0.99 以上，并且相干系数始终处于非常稳定的状态，充分说明了该次试验传递函数数据的可靠性。图7 中相干谱的初始阶段位置的陡峭主要是信号采集初始阶段的不稳定造成的，因为其占据的频率范围远小于所关心频率的最低数据(200 Hz 以上)所以可以忽略其不利影响。同时，图7a 中，传递函数相干系数在1 200 Hz 左右所出现的较小下降峰表明y14点在1 200 Hz 左右具有振动节点。

图7 所示的TFA 是基于复模态的数据分析，所以出现了测量点传函谱峰处对应相位的非规律变化。所以不能通过相位的延迟变化情况衡量测点振动的模态特性，并且单点的TFA 谱峰不能反映整个振动系统的模态情况。所以基于可靠的采集数据，需要进行滑块导轨完整振动系统的模态分析。

3.3 导轨滑块运动副试验模态参数分析

本次试验模态数据分析采用特征系统实现算法(eigensystem realization algorithm，ERA)进行计算分析。该方法是在直接模型识别基础上，根据采样得到的脉冲响应函数数据对振动系统的极点、模态参数和振型进行整体计算的多自由度时域算法［8-9］。同时，针对振动系统的频响函数数据，ERA 可以采用傅里叶逆变换得到对应的的脉冲响应函数，通过计算数据可以得到振动系统的模态频率、阻尼比、振型等诸多参数。

基于采集到的信号进行ERA 分析得到滑块导轨振动系统的前5 阶固有模态频率和阻尼比见表1 所示，各阶模态所对应的振型如图8 所示。

根据表1 测得的数据和图8 的振型，滑块导轨结合面阻尼比ζX和ζY分别为5.501 和3.098，滑块导轨振动系统的X向横荡和Y向垂荡固有频率分别为f2=566.818 Hz，f3=602.368 Hz。针对表1 所示阻尼比小于0.2 的导轨滑块粘性阻尼单自由度系统［6-7］，其阻尼和刚度计算如下:

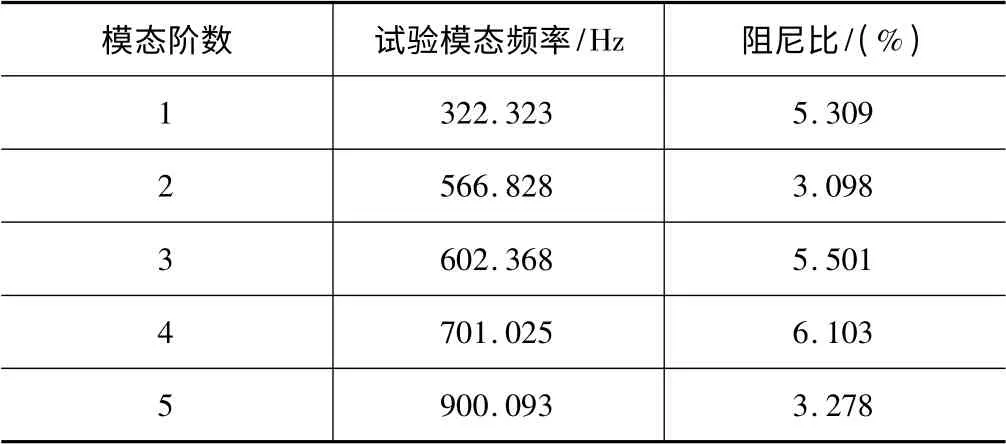
表1 滑块导轨的模态频率和阻尼比

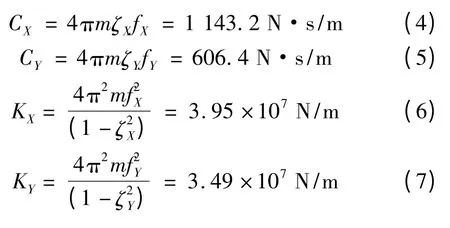
4 结语

本文以多功能机床的关键导轨滑块运动副为研究对象，阐述了试验模态分析以传递函数计算为基础的测试原理和方法。结合机床的受迫振动环境特点分析了导轨滑块运动副的受力分析，并构建了振动系统的振动模型和试验模态分析方案。并通过分析导轨滑块的结构特点，以试验模态的可行性分析为目标，结合试验模态信号数据的完整性分析，设置了试验模态测点方案。

基于试验模态测试数据，详细分析了试验得到的输入输出数据的合理性;并通过对试验传递函数的计算分析得到了机床关键导轨滑块运动副的前5 阶振动频率、阻尼和振型。结合试验数据确定了导轨滑块运动副的粘性阻尼振动系统特点，并计算得到了振动系统的阻尼和刚度。

试验模态分析结果为机床整体振动系统分析提供了关键导轨副的振动参数和建模依据。同时，试验过程的理论分析和试验数据处理方法为相关工程试验研究提供了借鉴。

［1］顾培英，邓昌，吴福生.结构模态分析及其损伤诊断［M］.南京:东南大学出版社，2008.

［2］杨橚，唐恒龄，廖伯瑜. 机床动力学［M］. 北京:机械工业出版社，1983.

［3］刘称意.考虑导轨结合面影响的数控机床动态特性分析及结构优化［D］.沈阳:东北大学，2010.

［4］张耀满.考虑直线导轨影响的数控机床动态性能分析［J］.东北大学学报:自然科学版，2007，28(11):1628 -1632.

［5］黄新.滚动直线导轨副性能分析及工程技术研究［D］.武汉:华中科技大学，2005.

［6］闻邦椿，刘树英，陈照波，等. 机械振动理论及应用［M］. 北京:高等教育出版社，2009.

［7］诸乃雄. 机床动态设计原理与应用［M］. 上海:同济大学出版社，1987.

［8］海伦.模态分析理论与试验［M］. 白化同，郭继忠，译. 北京:北京理工大学出版社，2001.

［9］杨景义，王信义. 试验模态分析［M］. 北京:北京理工大学出版社，1990.

［10］李德葆，陆秋海. 实验模态分析及其应用［M］. 北京:科学出版社，2001.

［11］应怀樵.现代振动与噪声技术第9 卷［M］. 北京:航空工业出版社，2011.