Investigation of the optimum differential gear ratio for real driving cycles by experiment design and genetic algorithm

AHMED Aboud, ZHAO Chang-lu (赵长禄), ZHANG Fu-jun (张付军)

(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)



Investigation of the optimum differential gear ratio for real driving cycles by experiment design and genetic algorithm

AHMED Aboud, ZHAO Chang-lu (赵长禄), ZHANG Fu-jun (张付军)

(School of Mechanical Engineering, Beijing Institute of Technology, Beijing 100081, China)

Experiment statistical method and genetic algorithms based optimization method are used to obtain the optimum differential gear ratio for heavy truck that provides best fuel consumption when changing the working condition that affects its torque and speed range. The aim of the study is to obtain the optimum differential gear ratio with fast and accurate optimization calculation without affecting drivability characteristics of the vehicle according to certain driving cycles that represent the new working conditions of the truck. The study is carried on a mining dump truck YT3621 with 9 forward shift manual transmission. Two loading conditions, no load and 40 t, and four on road real driving cycles have been discussed. The truck powertrain is modeled using GT-drive, and DOE -post processing tool of the GT-suite is used for DOE analysis and genetic algorithm optimization.

heavy trucks; fuel consumption; optimization; design of experiment; genetic algorithm; differential gear ratio

Vehicle performance and fuel economy for heavy trucks strongly depend on the driveline overall transmission ratio where vehicle maximum speed and torque are trade characteristics: increasing one of them will decrease the other. In addition, fuel economy also depends on the engine characteristics map, vehicle loading, driving conditions and road characteristics.

The Driveline overall gear ratio for manual transmission vehicles consists of transmission gear ratios, transfer case gear ratio and differential gear ratio. Heavy truck’s differential gear ratio is determined according to the torque and speed range required at the transmission output shaft, and the manual gear box number of gears and their gear ratios are chosen to fulfill the vehicle operation requirements. The first gear ratio governs the starting performance of the vehicle and is designed by the maximum torque desired at driving wheels and usually depends on the gradient of hill to be climbed at worst scenario with vehicle being fully loaded and the the engine working at low revolution. The last gear ratio is designed by the maximum speed desired at driving wheels and usually depends on the engine characteristics and the economy requirements at cruise speed. The intermediate gear ratio can be determined using the gear stability condition, where the engine speed must not exceed the maximum permissible speed when we gear down from one gear shift working at the maximum torque to the previous one. The intermediate gear ratio is usually spaced to provide an even and comfortable spread between the first and the last gears[1-2].

When changing vehicle working conditions such as maximum payload, road type, road slope, tires number and radius, the torque needed and speed range required at transmission output shaft will change and the total transmission ratio of the drive line needs to be adapted to the new conditions[3]. For most of these scenarios, changing the differential gear ratio is more convenient than redesign all drive line parts and change the transmission gear ratios.

In this study the mining dump truck YT3621 with 9 forward shift manual transmission was used on road cruising only and the optimum differential gear ratio that provides best fuel consumption for this new working condition was conducted using the GT-suite.

Investigation of different approaches that could optimize differential gear ratio was conducted using DOE-post processing tool of the GT-suite for DOE analysis and genetic algorithm. The results were discussed to determine the best approach that could be utilized to achieve accurate results in reasonable calculation time.

1 Modeling and simulation

Simulation models of the heavy duty mining dump truck YT3621 vehicle powertrain are established using GT-drive software. The analysis and optimization study is performed using DOE-post processing tool on the GT-suite platform.

1.1 Vehicle model

The heavy duty Mining Dump Truck YT3621 is a 6×4×10 vehicle with unloaded mass of 22 t and maximum payload of 40 t. The engine used is Weichai 11.596 L WD12.375 Diesel engine with maximum power of 275 kW at 2 200 r/min and maximum torque of 1 500 N·m. The truck was equipped with FAST 9JS180, 9 forward speed manual transmission.

Two detailed powertrain models are established using GT-Drive software, one for static simulation, and the other for dynamic simulation. The engine model used is based on looked up maps of the engine.

1.2 Static simulation

The simulation was conducted for tow loading cases: no load and 40 t load. The results show the vehicle’s dynamic performance limits, e.g. maximum speed, maximum gradability, maximum acceleration, etc. For the original differential gear ratio and the minimum possible gear ratio of the differential that can be used to maintain the heavy truck’s ability to follow the driving cycles of the study， the results were used to obtain the limits for possible shifting strategy speeds.

1.3 Dynamic simulation

Dynamic models are utilized and the model are controlled by the driving cycle data. The gear shifting for the models that used for the first approach is controlled by the vehicle speed, and the shifting speeds are set as different variables for each gear. The gear shifting for the models that used for the second approach is controlled by engine speed and is set as only one variable for all gears. The dynamic models and the software settings are fine-tuned to capture the fast speed variations in the used driving cycles to obtain accurate simulated driving cycle that matches the real one.

1.4 Driving cycles

Four on road driving cycles in Tab.1 with different criteria are used for the study to compare different driving situations Figs.1-2.

Tab.1 Driving cycle’s main characteristics

Fig.1 The 1st driving cycle

Fig.2 The 4th driving cycle

1.5 Genetic algorithm and DOE

DOE is a structured, organized statistical method which provides information about the interaction of factors and the way the total system works, something not obtainable through testing one factor at a time (OFAT) while holding other factors constant. Another advantage of DOE is that it shows how interconnected factors respond over a wide range of values, without requiring the testing of all possible values directly.

Genetic algorithms is a global optimization algorithm which is prevalent in many fields because of its simplicity, robustness and effectiveness[6]. It is used in many vehicle studies specially for multi-objective design problem optimization[7-8]to prove its effectiveness and reliability.

In this study the DOE post-processor of the GT-suite is used to run the dynamic simulation model of the truck for all the combinations of the variables which have been set for each optimization case, and then DOE post-processor establishes a statistical plan showing the results with respect to the study variables.

The optimization tool based on genetic algorithm optimization method of the DOE post-processor is used to obtain the objective function of the optimization which is the minimum total fuel consumption during the driving cycle in (gm/km), while excluding any driving cycle simulation results with error more than 1% compared with the original one.

2 Differential gear ratio optimization for minimum total fuel consumption

The study of the optimum differential gear ratio needed for YT3621 heavy duty Mining Dump Truck is conducted by using DOE as statistical analysis method and Genetic Algorithms as optimization methods to provide minimum fuel consumption for on road vehicle operation.

The study was conducted using four different situations on road driving cycles, two different loading conditions, no load and full load, the total of 8 different optimization study cases.

To optimize differential gear ratio for minimum fuel consumption we must also calculate the optimized shifting strategy that provides minimum fuel consumption for all studded differential gear ratios. So the optimization problem actually consists of two levels of optimization, which are the gear shifting strategy optimization and the differential gear ratio optimization.

① For the differential gear ratios, they are chosen between the original ratio of 11.27 and the minimum possible ratio that can follow the real driving cycles used in the study. The minimum possible ratio is calculated from the static simulation and the value is 5. The accuracy of the optimization results will increase as gear ratios between these two values increase.

② For the gear shift strategy there is more than one optimization variable, and actually the number of variables to be optimized equals the number of gear shifts used during driving cycles, which unfortunately varys according to the deferential gear ratio value. There will be three gears to be optimized in case of using the original differential with gear ratio of 11.27, while the number of gear increases to five for the minimum differential gear ratio of 5.

Using the method in Ref.[4] to solve the optimization problem utilizing GT-suite DOE-post processing tool, there are two challenges.

① The first is that the speed range for each gear shift will change when the differential gear ratio varies, so it is impossible to curry out the optimization problem with the two levels together.

② The second is the time to solve the optimization problem with all this variables. For example: if each loading case and each driving cycle use 5 different differential gear ratios and take 5 speed steps for each gear shift, and we have 5 gear shifts during driving cycle simulation, we will have about 16 525 simulation run. Knowing that the time needed to compute a driving cycle of 2 000 s with accepted accuracy is about 30 minute using INTEL CORE i5 PC, It takes about one year for each of the 8 study cases.

To solve the first challenge, the dynamic model was modified such that the gear shifting is controlled by engine speed instead of vehicle speed so changing the final drive will not affect the range of chosen shifting speeds.

To solve the second challenge, we need to minimize the number of variables or the number of steps per variable or both without affecting the accuracy of optimization.

To reduce the number of speed steps for gear shifting variables, we used the results of a study conducted on the fuel consumption of the YT3621 heavy duty Mining Dump Truck at all possible ranges of operating conditions to find the optimum running speeds and shifting strategy that provide best fuel economy of this truck[5]. From this study we found that the engine working points of the gear shifting that provides best fuel economy for all gear shifts and all loading conditions are located between 1 200 r/min and 1 600 r/min Fig.3. Based on this study, we can reduce the number of speed steps for each gear shift to 4 without affecting the optimization accuracy. But according to the example mentioned above, we still have about 106 days for each of the 8 study cases. Therefore variables need to be reduced to avoid this long calculation time.

Fig.3 Enginespeeds of gear shifting that provide best fuel consumption

To reduce the number of variables of the optimization, we have two approaches:

① The first approach is to exclude different gear ratios from the optimization problem and to consider it as a study case variable like load condition and driving cycles. Using this approach we have 40 study cases instead of 8 but the optimization variables was considerably reduced especially for high differential gear ratios. The time for each case study was reduced to about 21 days for low differential gear ratios and about 32 hour for high differential gear ratios. The greater number of study cases and the less time for each case calculation are more useful when using more PC’s in the simulation. The main drawback of this approach is that choosing the best different gear ratios is not actually optimized from the study cases results. To optimize using this approach we used four different differential gear ratios.

② The second approach is to optimize the gear shifting using engine speed instead of vehicle speed and to consider it as one variable for all gear shifts to get the optimum gear shifting speed. This will reduce optimization variables to only two for all study cases and reduce the time of each case to 10 h only.Even by increasing the steps for each of the two variables to 10, the time needed will not exceed 50 h, and we still have only 8 study cases. The main drawback of this approach is the gear shift strategy optimization error compared to the original method. To evaluate this error, recalculation the optimum gear shifting strategy that studded in Ref.[4] using this approach was conducted and the results were compared with the original study as shown in Tab.2.

The calculation shows that the maximum error when using only one optimized gear shifting speed for all gear shifts was 0.67%. So this approximation can be used when the expected fuel saving is much higher than this error percentage.

Tab.2 Percentage of error between fuel optimization results using individual gear shifting speed optimization and one gear shifting speed optimization

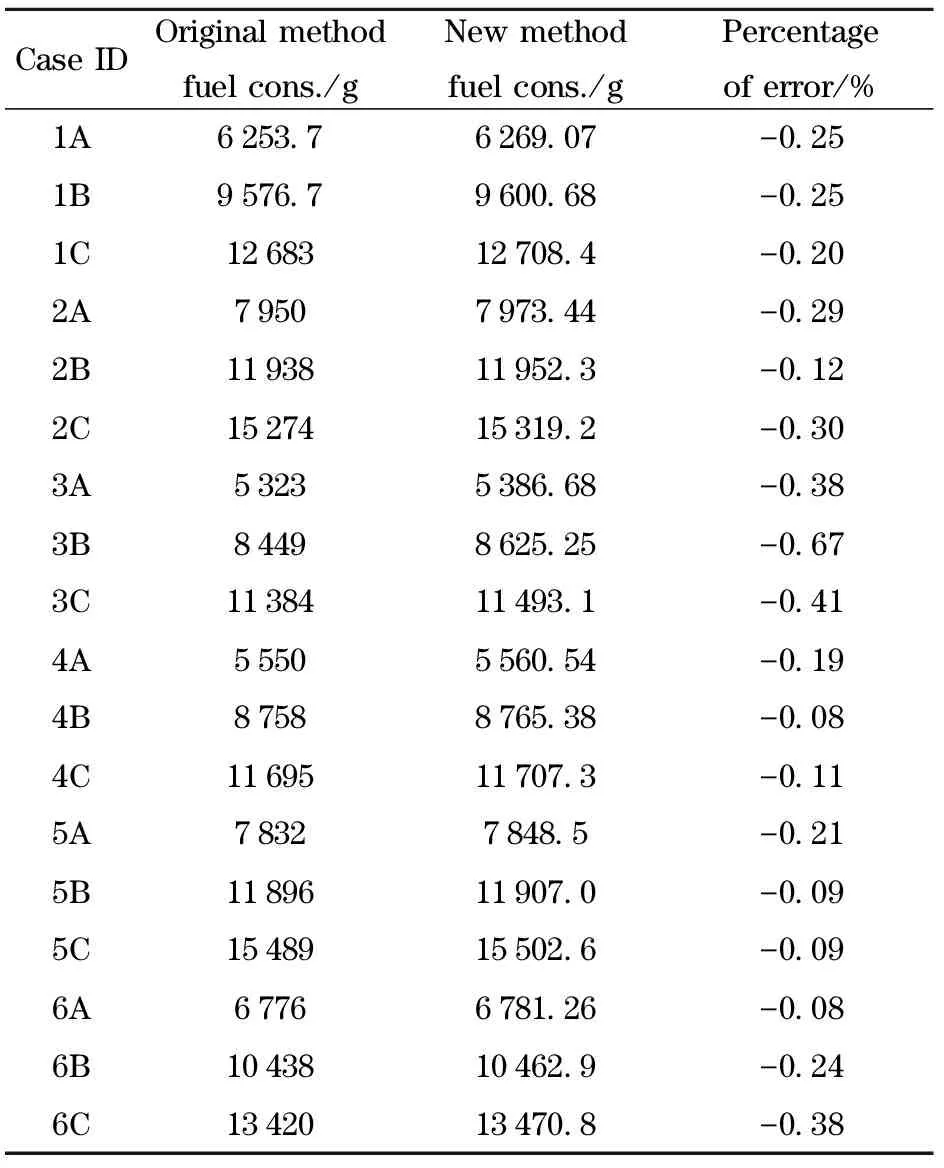
CaseIDOriginalmethodfuelcons．/gNewmethodfuelcons．/gPercentageoferror/%1A6253 76269 07-0 251B9576 79600 68-0 251C1268312708 4-0 202A79507973 44-0 292B1193811952 3-0 122C1527415319 2-0 303A53235386 68-0 383B84498625 25-0 673C1138411493 1-0 414A55505560 54-0 194B87588765 38-0 084C1169511707 3-0 115A78327848 5-0 215B1189611907 0-0 095C1548915502 6-0 096A67766781 26-0 086B1043810462 9-0 246C1342013470 8-0 38

3 Simulation results and analysis

3.1 DOE statistical results analysis

After each of the DOE simulation case run is finished, the response surface (statistical data plan) for the total fuel consumption of the driving cycle is created, and the quality of the surface fit is checked. The maximum fit error found for all optimization cases was 0.83% and the average error was 0.42%.

The relative significance of each gear shift on the total fuel consumption and how shifting speed change affecting the total fuel consumption for each individual gear shift, and the four gear shift interactions are studied for each DOE run to determine the relative importance of each gear shifting on total fuel consumption table.

3.2 GA optimization results and analysis

3.2.1 First approach results

The gear shifting speeds for the minimum total fuel consumption of the driving cycles were optimized for each of the 40 study cases, and these gear shifting speeds obtained from genetic algorithm optimization are used to run the dynamic simulation model. The fuel consumption calculated from the dynamic model with optimized gear shifting speeds was then compared with the fuel consumption calculated from the genetic algorithm optimization for the 40 study cases, and the maximum error from genetic algorithm optimization was less than 0.23%.

The change of the total fuel consumption with the final drive ratio for each load condition and each driving cycle are shown in Fig.4.

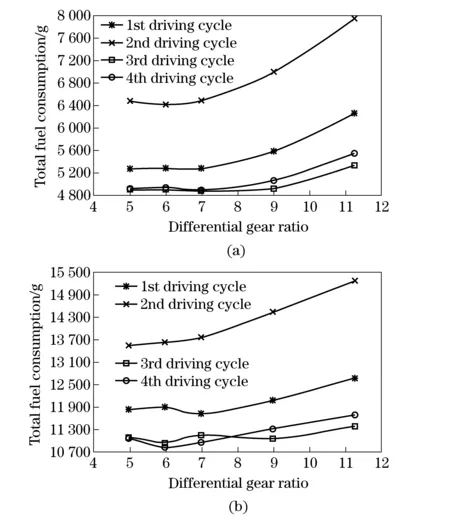
Fig.4 Optimized total fuel consumption for the study driving cycles at no load and 40 t load

From these results the percentage of possible fuel saving for each differential gear ratio optimization case was compared to of the original differential gear ratio are shown in Tab.3.

The result shows that there is a big reduction in fuel consumption when reducing differential gear ratio from 11.27 to 9 and also there is other significant reduction when the ratio reduced to 7. There are minor changes up and down when the ratio reduced to 6 and 5. The results show that the best fuel consumption is obtained by using differential gear ratio between 7 and 5. To determine exactly which ratio is the optimum ratio for the all driving cycles we must repeat the calculations for at least ten differential gear ratios between 5 and 7, which will take very long time.

3.2.2 Second approach results

The optimization results of differential gear ratio and the shifting engine speed that provide minimum total fuel consumption for the 8 cases of study are shown in Tab.4. In addition, the percentage of fuel saving of the optimized results comparing with that obtained from the vehicle original differential gear ratio of 11.27 are also presented in the table. According to the results, it is clear that the optimum final drive gear ratio is between 6 and 7 for the all the study cases.

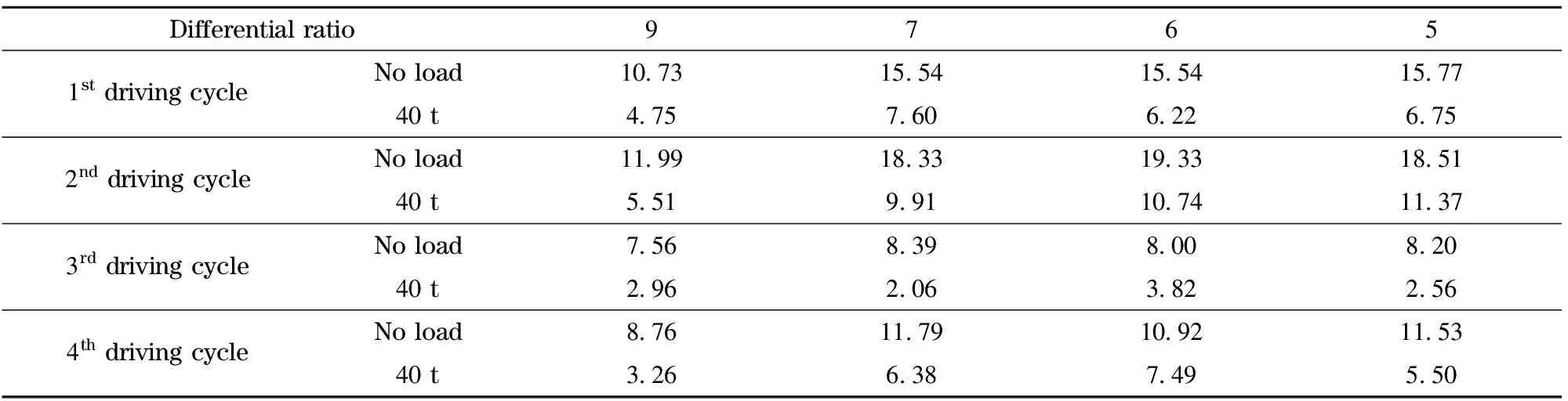
Tab.3 Percentage of total fuel saving from the first differential gear ratio optimization approach compared to the original differential gear ratio %

Tab.4 Results of the second differential gear ratio optimization approach with the percentage of the total fuel saving compared to the original differential gear ratio

3.2.3 Comparing the results of the two approaches

Although the first approach gives more accurate results due to individual gear shifting speed optimization, its huge amount of time for calculation makes it too difficult to run enough differential gear ratio cases for accurate results. The second approach gives fast and reasonable optimized solution and the number of differential gear ratio steps can increase to obtain accurate results without computational time issue. The results show higher fuel saving percentage than that obtained from the first approach in most cases as shown in Tab.5 except for only two cases showsingmore fuel saving for the first approach with very minor difference.

The results from the first approach shows that the optimum differential gear ratiois located between 5 and 7. Because we only have results at gear ratio of 5, 6 and 7 we cannot determine one optimum differential gear ratio that suit all driving cycles and loading conditions used in the study.

The second approach shows that the optimum differential gear ratiois located between 6 and 7 and we have enough results of the different differential gear ratios to find the optimum differential gear ratio that is suitable for all driving cycles and loading conditions.

Tab.5 Comparing the fuel saving percentage obtained from the two approaches %

3.2.4 Obtaining the optimum differential gear ratio for the truck on road operation

To find the optimum differential gear ratio that suit all driving cycles and loading conditions, we used the second approach results to calculate the percentage of the total fuel consumption saving at the optimum differential gear ratio. The results were compared to that at the other differential gear ratios between 6 and 7 for each study case as shown in Fig.5. The mean value of the total fuel consumption saving percentage was calculated at each differential gear ratio between 6 and 7 as shown in Fig.6. Based on the lowest fuel consumption percentage mean value, the optimum deferential gear ratio that provides minimum total fuel consumption for all study cases is determined as 6.5.

Fig.5 Percentage of the total fuel consumption saving at the optimum differential gear ratio compared to that at the other differential gear ratios for each study case

Fig.6 Mean value of the total fuel consumption saving percentage

3.3 Optimization results verification

The gear shifting engine speeds and differential gear ratios for minimum fuel consumption that obtained from genetic algorithm optimization calculations for both approaches are used to run the dynamic simulation model. The fuel consumption calculated from the dynamic model was compared with the fuel consumption calculated from the genetic algorithm optimization, and the error of the optimization method was calculated and presented in Tab.6 and Tab.7.

3.4 Simulated driving cycles verification

The setting of the simulation software is tuned for both approaches and all cases such that error between the dynamic simulation driving cycle and the real driving cycle for each case is less than 0.1%. The genetic algorithm optimization of the DOE post-processor was adapted to exclude any driving cycle simulation results with error more than 1%. Random simulation runs for all study cases were selected and comparison between the real driving cycle and the driving cycle obtained from the dynamic simulation was conducted (Fig.7).

Tab.6 Error between minimum total fuel consumption calculated from GA optimization and that from dynamic simulation for the first approach %

Tab.7 Error between minimum total fuel consumption calculated from GA optimization and that from dynamic simulation for the second approach

Fig.7 2nd driving cycle dynamic simulation verification

4 Conclusions

①DOE and genetic algorithms could be effectively used together to achieve fast and accurate solutions for multi-objective vehicle powertrain optimization problems.

②In complicated powertrain optimization problems where too much variables are presented and the expected simulation runs are very high, reducing the gear shifting optimization to only one variable for all gear shifts will dramatically reduce the number of the needed simulation runs without notable effect on the accuracy of the results.

③According to the results from the studied cases, changing differential gear ratio is very important when changing vehicle operating conditions or tire diameter to adapt the new range of torque and speeds at transmission output and to maintain fuel economic operation of the vehicle. In this study changing the differential gear ratio of the heavy duty mining dump truck YT3621 to suit on road operation can save up to 19% of the total fuel consumption comparing with the original differential gear ratio.

[1] Happian-Smith. An introduction to modern vehicle design[M]. Amsterdam: Elsevier, 2001.

[2] Mashadi B, Crolla D. Vehicle powertrain system[M]. New York: John Willey & Sons, 2012.

[3] Guzzella L, Sciarretta A. Vehicle propulsion systems[M]. Berlin: Springer, 2005.

[4] Ahmed A, Zhao C L, Han K, et al. Using design of experiment and genetic algorithm to obtain the optimum gear shifting strategy for a real driving cycles[J]. Applied Mechanics and Materials, 2012, 224: 497-503.

[5] Ahmed Aboud, Zhao Changlu, Mohamed K Khalil. Finding the optimum driver behavior for a heavy truck with manual transmission using GT-drive[C]∥ICAMECE 2012, Pattaya, Thailand,2012.

[6] Jiang-hua F, Wen-ku S, Teng T, et al. Optimization of automotive powertrain mounting system based on adaptive genetic algorithm [C]∥Intelligent Information Technology Application, 2009. IITA 2009. Third International Symposium on IEEE, 2009, 1: 347-350.

[7] Fujita K, Hirokawa N, Akagi S, et al. Multi-objective optimal design of automotive engine using genetic algorithm[J]. Power, 1998, 200(150): 100.

[8] Liu X, Wu Y, Duan J. Optimal sizing of a series hybrid electric vehicle using a hybrid genetic algorithm[C]∥Automation and Logistics, 2007 IEEE International Conference on IEEE, 2007: 1125-1129.

(Edited by Wang Yuxia)

10.15918/j.jbit1004-0579.201524.0110

TK 421 Document code: A Article ID: 1004- 0579(2015)01- 0065- 09

Received 2013- 06- 06

E-mail: clzhao@bit.edu.cn